制造氢气瓶内胆的电加热滚塑工艺参数的优化研究

刘学军

（北京工商大学计算机与人工智能学院，北京 100048）

0 前言

氢能是目前国家大力发展的清洁能源，而氢气瓶是储存和运输高压氢气的重要装置。内胆采用塑料材料的氢气瓶即IV 型氢气瓶与其他类型的氢气瓶相比，质量更轻、耐久性更好、储气量更大［1］。目前有不少IV型氢气瓶的内胆采用注塑工艺，但注塑工艺不适宜于直接制造中空形的部件，必须配合后续的焊接工艺［2］。而滚塑工艺非常适合于制造中空形部件，并具有模具成本低、制品壁厚均匀、无焊缝、几乎无内应力等优点［3］。因此国内外都在研发采用滚塑工艺制造IV 型氢气瓶的内胆。

以往最常用的滚塑工艺是将模具放置在一个烘箱内，通过热空气循环对流的方式来对其进行加热，但这种烘箱加热方式的能量利用率非常低［4］。为了降低能耗，近些年来对滚塑模具开始采用其他的加热方式如油加热［5］、微波加热［6］、电加热的方式［7-8］。而采用电加热的滚塑工艺不仅可以节能还便于对整个工艺过程进行自动化控制，因此研究通过电加热滚塑工艺来制造IV型氢气瓶的内胆具有重要的实际意义。

为氢气瓶内胆的电加热滚塑工艺建立传热模型并进行仿真计算是对氢气瓶内胆进行研发的有效手段之一。以往已有大量的研究为采用烘箱加热方式的滚塑工艺建立了不同的传热模型并进行了仿真计算，这些传热模型主要包括tumbling 模型［9-11］和static bed 模型［12-13］。但由于电加热方式与烘箱加热方式的不同，在为电加热的滚塑工艺建立模型时需要进行一些修改。本文是在static bed 模型的基础上重新设置了在模具外表面的热边界条件。对于在烘箱里受热的滚塑模具，只要知道了烘箱内的加热温度以及模具的表面传热系数，则可在其外表面上采用第三类热边界条件。从物理意义上来讲，这个边界条件使得烘箱内高温空气的热量持续地传给了模具及模内粉料和空气。而本文所研究的是一个在其外表面嵌入电热丝的滚塑模具，需要将电热丝的发热量转换为模具的内热源。另外在模具的外表面也需要设置第三类热边界条件［14］，但这个边界条件是为了将模具内电热丝的发热量中的一部分通过热辐射、对流换热和导热分别传给外界环境壁面、环境空气以及与模具相连的模架等附件。另外本文所采用的电加热方式是PID 控制模式，也就是说加热功率在整个加热过程并不是恒定的，因此在模具外表面所设置的内热源强度也必须随时间变化。但这个加热功率随时间变化的数学函数关系事先并不知道，因此如何设置内热源强度是一个难点。

在本文所研究的滚塑机的控制器上有3 个工艺参数，即初始加热功率的百分比、PID 模式的触发温度以及停止加热时的模内温度。在加热过程开始后，模具的温度从初始值快速升高。此时控制器输出的加热功率是个恒定值，它与满负荷功率即电热丝的最大加热功率的比值就是上述第1 个工艺参数的含义。当模具的表面温度升高到某个预设值时，PID 控制模式即被触发，此后加热功率被动态地调整以使得模具的表面温度保持在不超过预设值的一个很小范围内波动。该预设值就是上述第2个工艺参数的含义，也就是说在整个加热阶段模具的最高温度不能超过PID 模式的触发温度，这对节能和避免模具过热都是有好处的。以PID 模式被触发的时刻为分界点，在此之前的加热阶段称为升温段，在此之后的加热阶段称为保温段。当模内温度升高到某个合适的数值时就可以给电热丝断电，即整个加热阶段结束，这个温度值就是上述第3 个工艺参数的含义。该温度并不是模内空气的最高温度，因为当停止加热时，虽然模具温度开始降低，但模内的温度由于热惯性还会继续升高。在本文停止加热时的模内温度设置成能使得模内的最高温度刚好等于200 ℃，因为这样可以将塑料制品内部的气泡基本排除，从而使制品具有最佳的力学性能［15］，显然停止加热时的模内温度应该比200 ℃低一些。目前在实际操作中，该工艺参数是根据经验设置的，有可能使得模内实际的最高温度与200 ℃偏差较多，从而影响产品品质。可以看出当初始加热功率的百分比、PID 模式的触发温度这2个工艺参数确定后，停止加热时的模内温度也就相应确定了。

近些年来，灰度关联度分析也被用于塑料成型工艺参数的优化研究中。简单来说，该方法就是通过计算各因素的灰色关联度的极差并对其进行排序以确定各因素对指标影响程度的大小。文献［16］通过灰色关联度分析对双色塑料碗的注塑工艺进行了多目标的参数优化。而文献［17］则应用该方法从若干种候选塑料中选出最适合于滚塑工艺的材料。

本文所采用的滚塑模具是一个绕双轴转动的电加热铝制模具，用来制造氢气瓶内胆。首先在static bed模型的基础上建立一个适用于PID 控制模式下的电加热滚塑工艺的传热模型，并通过FLUENT 软件对其进行仿真计算，将仿真结果与实验数据相比较从而验证了本文的传热模型。然后应用该模型仿真计算了16种情形，即4 种PID 模式的触发温度与4 种初始加热功率的百分比的组合情形。根据仿真结果分别研究了停止加热时的模内温度、加热时间以及加热电能与这2个工艺参数的关系，从而确定了最佳的工艺参数组合。最后通过灰度关联度分析得出了这2 个工艺参数分别对加热时间和加热电能的影响程度，从而为电加热滚塑工艺参数的设置和优化分析提供了理论方法和可供参考的结论。

1 传热模型的建立

如图1所示，本文采用的是滚塑工艺的static bed模型，即假设在整个工艺过程粉料或熔融塑料层都均匀且紧密地黏附在模具的内壁面上。通过FLUENT软件进行仿真计算可得出模具表面和模内温度、加热时间以及加热电能。仿真的区域包括模具、塑料层和模内空气。实际的模具还包括法兰和封头，其外表面还刻有用来嵌入电热丝的凹槽，形状比较复杂。为减小计算量，本文将模具简化为与氢气瓶内胆的外形完全一样且表面光滑的薄壳体。可计算出简化后模具的厚度为9.9 mm，以保证简化后模具的质量等于实际模具的质量（9.4 kg）。

图1 电加热滚塑工艺的static bed模型Fig.1 Static bed model of rotational molding process heated electrically

在模具的外表面上设置第三类热边界条件。从模具的外表面向其内部形成一个1 mm 厚的薄层，在该薄层里设置一个强度为qv的内热源。该内热源强度在升温段是大小恒定的，在保温段需要动态地调整以模拟PID 模式被触发后随时间变化的功率输出。内热源强度qv按照式（1）计算。

式中p——在升温段为初始加热功率的百分比；在保温段为动态调整的加热功率的百分比

Q——满负荷加热功率即电热丝的最大发热功率，W

V——在模具外表面的内热源体积，m3

当模具的表面温度升高到PID 模式的触发温度时，加热阶段进入保温段，加热功率开始动态地调整以保持模具的表面温度在不超过该触发温度的狭小范围内波动。在保温段，加热功率随时间的变化规律是一个未知的复杂函数。本文并不试图得到这个函数关系式，而是按如下方式处理。当PID 控制模式被触发后，首先将加热功率减小到满负荷功率的50 %，然后持续观察模具表面温度随时间的变化。每当模具的表面温度即将下降到比所设置的触发温度低5 ℃时，则将加热功率的百分比增大10 %；每当其升高到即将超过该触发温度时，则将该百分比减小10 %。总之是将模具的表面温度限制在PID 触发温度到其值以下的5 ℃范围内。每当需要调整加热功率的百分比时，则先暂停计算，相应地修改在外表面热边界条件中的内热源强度后继续仿真计算。当模内温度升高到能使得最高的模内温度刚好为200 ℃时，将内热源强度设为0。即模拟在此时加热丝断电，加热阶段结束，此温度即为停止加热时的模内温度。在仿真过程中，可根据经验先预估一个温度值作为停止加热时的模内温度进行试算。如果仿真所得的最高模内温度超过200 ℃，则将下一个预估值设定为当前预估值减去这二者之差的绝对值，即在下一次仿真中需要提前结束加热；反之则将下一个预估值设定为当前预估值加上这二者之差的绝对值，即在下一次仿真中需要推迟结束加热。不断重复上述试算直至仿真所得的最高模内温度与200 ℃之差足够小为止，此时所采用的当前预估值即为停止加热时的模内温度。

在确定了停止加热时的模内温度后，就可以得到滚塑工艺在加热阶段所花费的时间即加热时间。另外再对模具的内热源强度随时间变化的阶梯形曲线进行积分，即可算出该滚塑工艺所消耗的加热电能。需要说明的是本文所研究的加热电能指的是电热丝为加热模具所消耗的电能，不包括滚塑机的电机为驱动双轴转动所消耗的电能，后者比前者小很多，可以暂时不考虑。

在仿真计算过程中，以模内的粉料刚开始熔融的时刻为分界点，在此之前采用塑料层和模内空气的质量平均温度作为仿真所得的模内温度；在此之后则采用模内空气的温度作为仿真所得的模内温度，并将刚开始熔融时塑料层和模内空气的质量平均温度同时作为塑料层和模内空气的初始温度继续进行随后的仿真计算。

2 计算参数的设置

本文所研究的粉料为线性低密度聚乙烯，其牌号为M3204RUP，粉料的表观密度为317 kg/m3，真实密度为932 kg/m3，熔点为125 ℃，生产厂家为泰国SCG ICO有限公司。滚塑机的内、外轴转速分别设定为11、1.2 r/min。成型后的氢气瓶内胆尺寸如图2所示，其设计厚度为8 mm。在模具外表面所嵌入的电热丝的总长度为12.37 m，每单位长度电热丝的最大发热功率为700 W/m，因此在式（1）中的满负荷加热功率为Q=8 659 W。

图2 氢气瓶内胆的剖面形状和尺寸Fig.2 Cross section and dimension of liner of hydrogen cylinder

空气的比热容为ca=1 014 J/（kg·K），模具材料的比热容为cm=904 J/（kg·K）。粉料的平均比热容cp和热导率k分别为2 201.2 J/（kg·K）和0.17 W/（m·K）［18］，粉料的熔融潜热L为180 000 J/kg［9］。模具的外表面积Ao为0.378 m2，环境空气的温度Tf为30 ℃。由实验测得在加热阶段模具外表面平均的传热系数ho为44.2 W/（m2·K）。仿真计算的情形是指将4 种初始加热功率的百分比（70 %、80 %、90 %、100 %）与4种PID模式的触发温度（220、230、240、250 ℃）组合而成的16种情形。

3 传热模型的验证

图3 分别显示了模具外表面和模内的仿真温度与其实测温度随时间的变化规律。设置的2 个工艺参数分别为初始加热功率的百分比等于70 %，PID 模式的触发温度等于230 ℃。在仿真中和实验中所采用的停止加热时的模内温度都等于175.6 ℃。可以看出在整个加热阶段模具外表面和模内的仿真温度与其实测温度都吻合得较好，但在加热阶段结束后前者比后者都要偏低一些。这是因为在电热丝刚断电时，模具外表面的温度下降得比模架的温度要快，即在某个时间段与模架相接触的模具表面局部位置处的温度会低于模架的温度。致使模架以前在加热阶段积蓄的热量开始向模具传递，相当于在电热丝断电后模架对模具起到了另外一个内热源的作用。但本文的仿真区域并不包括模架，因此在仿真计算中没有考虑这个内热源，从而使得在电热丝断电后仿真所得的模具外表面和模内温度都偏低一些。但随着冷却过程的进行，模架温度会逐渐与模具的外表面温度趋于相同，此后模架不再向模具传递热量，模具外表面和模内的仿真温度与其实测温度的吻合程度变得越来越好。

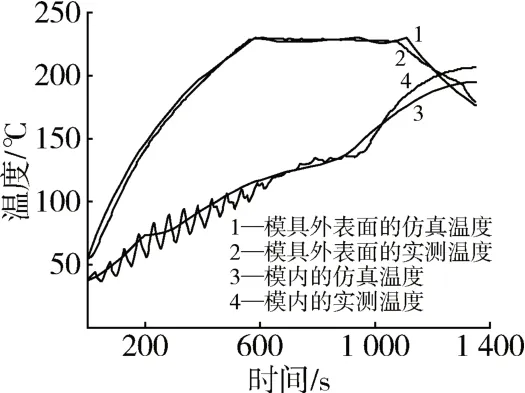
图3 模具外表面和模内的仿真温度与实测温度的比较Fig.3 Comparison of simulated temperatures with tested temperature at outer surface of and inside mold

图4 表示了在对上述实验情形的仿真计算中加热功率的百分比随时间呈阶梯形变化的规律。这个动态调整的加热功率可以保证进入保温段后模具的表面温度在PID 模式的触发温度与低于其5 ℃之间的范围即225～230 ℃内波动。求出图4 所包含的面积再乘以满负荷功率即可得到加热电能的仿真值。

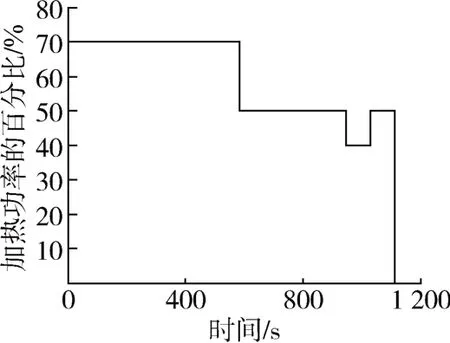
图4 在对实验情形的仿真中加热功率的百分比随时间的变化Fig.4 Variation of percentage of heating power with time in simulation for experimental case

表1分别给出了加热时间、加热电能、模内最高温度的仿真结果和实验结果以及二者间的相对误差。在确定加热时间和加热电能之前需要知道加热阶段的终点。如上所述，无论是在仿真还是实验中加热阶段的终点都选在模内温度达到175.6 ℃的时刻。实验测得在加热阶段的总耗电量为1.76 kW•h，电机驱动滚塑机双轴转动的功率为660 W，扣除该驱动功率所消耗的电能后即可得到实际电热丝的加热电能为1.563 kW•h。由表1可以看出加热时间和加热电能的仿真值与实测值的相对误差都很小，只是模内最高温度的相对误差更大一些。

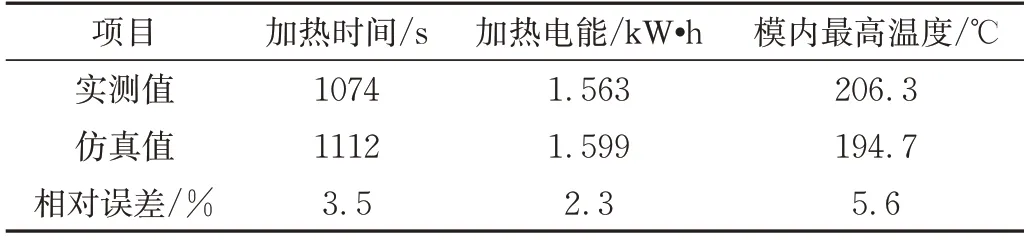
表1 加热时间、加热电能、模内最高温度的实测值和仿真值及其相对误差Tab.1 Tested and simulated values of heating time，and electrical energy and highest temperature inside mold and relative errors between them

4 结果与讨论

4.1 工艺参数对停止加热时模内温度的影响

通过本文传热模型的仿真结果可以研究初始加热功率的百分比和PID 模式的触发温度对停止加热时模内温度的影响。从图5可以看出，停止加热时的模内温度随初始加热功率的百分比变化较小，而且在PID 模式触发温度越高的情形，该变化就越小。这说明在实际操作中如果以前设置的工艺参数可以获得满意的塑料制品，现在只需要调节初始加热功率的百分比，那么基本上没有必要去重新设置停止加热时的模内温度。另外由图5还可以看出，该模内温度随PID模式触发温度的升高而降低。这是因为当模具处于较高温度时，模具和模内的熔融塑料都具有较高的热容量，即其热惯性比较大，可以向模内空气传递更多的热量。因此需要在较早的时刻即模内温度较低时将电热丝断电才能使得模内空气的最高温度刚好达到200 ℃。

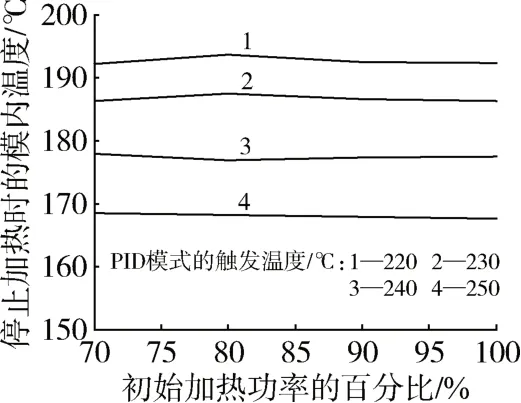
图5 停止加热时的模内温度随初始加热功率的百分比的变化Fig.5 Variation of temperature inside mold while heating being stopped with percentage of initial heating power

4.2 工艺参数对加热时间和加热电能的影响

由图6 可知，在4 种加热功率的百分比下，加热时间都是随PID 模式的触发温度的升高而减少，并且随之减少的速率逐渐变缓。这是因为随着PID 模式触发温度的升高，即允许模具保持的最高温度变大了，因此模内粉料能更早地开始熔融，也能更早地结束熔融，这样就能更早地让电热丝断电，从而缩短了加热时间。

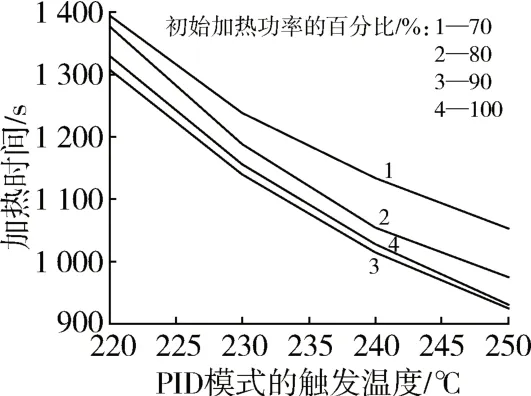
图6 加热时间随PID模式的触发温度的变化Fig.6 Variation of heating time with trigger temperature of PID mode

由图7 可知，在4 种PID 模式的触发温度下，加热时间都是先随着初始加热功率的百分比的增大而减少，但当该百分比达到90 %时加热时间随之反而略微增加，而且这个增加量随着PID 模式触发温度的升高而减小。这说明当初始加热功率的百分比达到90 %时，在其他条件保持不变的前提下继续增大该加热功率对提高滚塑工艺的生产效率已经没有效果了。

图7 加热时间随初始加热功率的百分比的变化Fig.7 Variation of heating time with percentage of initial heating power

在图7中加热时间的这种变化规律可能是因为，在熔融过程刚开始时，由于大部分的模内粉料还没来得及被充分加热，因此粉料熔融的速率很低。当加热功率的百分比不超过90 %时，偏低的粉料熔融速率所持续的时间比较短，对熔融过程完成的拖累效果并不明显，因此它不会改变加热时间随加热功率的增大而减少的规律。但是当加热功率的百分比达到90 %时，如果继续增大加热功率，虽然能使得模具的温度更快地升高，但温度来不及跟着升高的模内粉料所占比例也会更大。因此在熔融过程前期偏低的粉料熔融速率所持续的时间就会更长，从而对熔融过程完成的拖累效果就会变得更明显，致使加热时间不降反升。但是在PID 模式的触发温度较高的情形下，由于模内粉料开始熔融的时刻大大提前了，从而使得上述的拖累效果又被抵消掉了一部分。因此当加热功率的百分比增大到超过90 %时，加热时间随之就增加得很少。

由图8 可知，在4 种初始加热功率的百分比下，加热电能都是随PID 模式的触发温度的升高而减少，并且随之减少的速率逐渐变缓。这与前述的加热时间随之变化的规律相同，显然滚塑工艺所花的加热时间短了，相应地所消耗的加热电能也就少了。由此可见对于电加热滚塑工艺，为最大限度地提高生产效率和节能，应尽可能地提高PID 模式的触发温度，即让模具一直处于较高的温度范围内运转。但是较高的模具温度也会带来不利的地方。这是因为熔融塑料在250 ℃时更容易发生氧化降解，致使塑料制品的冲击强度大幅度降低［3］。其次目前使用的电加热滚塑模具为铝制模具，铝的熔点较低，较高的模具温度也会降低模具以及其上测温探头的使用寿命。另外由图6 和图8 可以看出，当PID 模式的触发温度已经较高了，继续提高该值从而在生产效率和节能方面带来的收益变得越来越小，与由此带来的不利相比也得不偿失。因此最好将模具的最高温度即PID模式的触发温度限制在250 ℃。

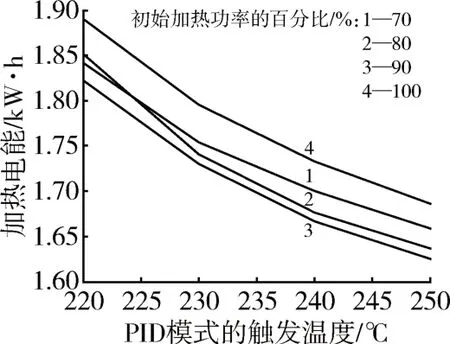
图8 加热电能随PID模式的触发温度的变化Fig.8 Variation of heating electrical energy with trigger temperature of PID mode

由图9 可知，当PID 模式的触发温度为230、240、250 ℃时，加热电能随初始加热功率的百分比的增大先是慢慢减少然后急剧增大。当该温度为220 ℃时，加热电能随加热功率的百分比先是微增然后减小再急剧增大。由此可以看出提高初始加热功率是可以节能的，但如果将该值提高到满负荷功率，反而大大增加了加热电能。将图9 与图7 相比较可以看出，当初始加热功率的百分比从90 %增大到100 %，加热电能增加的幅度要远大于加热时间增加的幅度。从生产效率的角度来讲，最差的工艺参数是PID模式的触发温度取220 ℃以及初始加热功率的百分比取70 %；从节能的角度来讲，最差的工艺参数则是该触发温度取220 ℃以及该功率百分比取100 %。但无论从生产效率还是节能的角度来讲最优化的工艺参数都是PID 模式的触发温度取250 ℃以及初始加热功率的百分比取90 %。

图9 加热电能随初始加热功率的百分比的变化Fig.9 Variation of heating electrical energy with percentage of initial heating power

4.3 灰色关联度分析

可采用灰色关联度分析方法来进一步研究PID 模式的触发温度和初始加热功率的百分比分别对加热时间和加热电能的影响程度的大小。首先将所有16种仿真情形的条件和计算结果列于表2，每一种仿真情形的条件明确了上述这2个工艺参数的大小。将加热时间和加热电能选为优化指标，将每一种仿真情形的计算结果看作一次实验的结果，每个工艺参数都按4 个水平来变化。

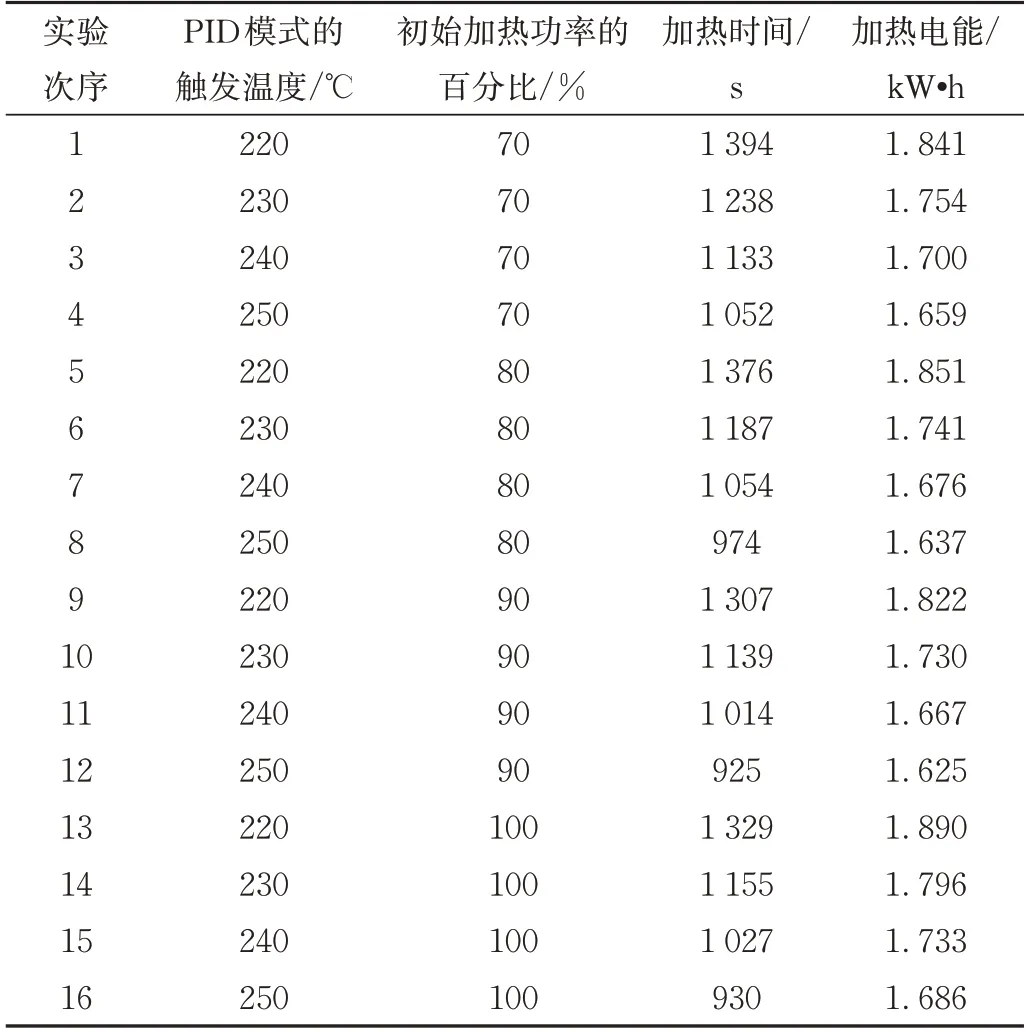
表2 16种仿真情形的条件和计算结果Tab.2 Conditions and computational results in 16 simulated cases

根据文献［16］中的公式分别计算出加热时间和加热电能的信噪比、无量纲化的信噪比以及灰色关联度，将它们的计算结果列于表3，分别用符号X和Y表示。

表3 信噪比、无量纲的信噪比和灰色关联度的计算结果Tab.3 Computational results of SNR，dimensionless SNR and grey relational grade

针对加热时间和加热电能，分别计算PID 模式的触发温度和初始加热功率的百分比这2 个工艺参数在不同水平下的灰色关联度的平均值，然后计算这些平均值的极差并对其进行排序，所得结果分别表示在表4和表5中。极差越大，表示该工艺参数对优化指标的影响就越大。由表4 和表5 可知，无论是加热时间还是加热电能，都是受PID 模式的触发温度的影响程度要大于受初始加热功率的百分比的影响程度。因此在不使熔融塑料发生氧化降解的前提下，应优先考虑将电加热的滚塑模具维持在尽可能高的温度范围内。

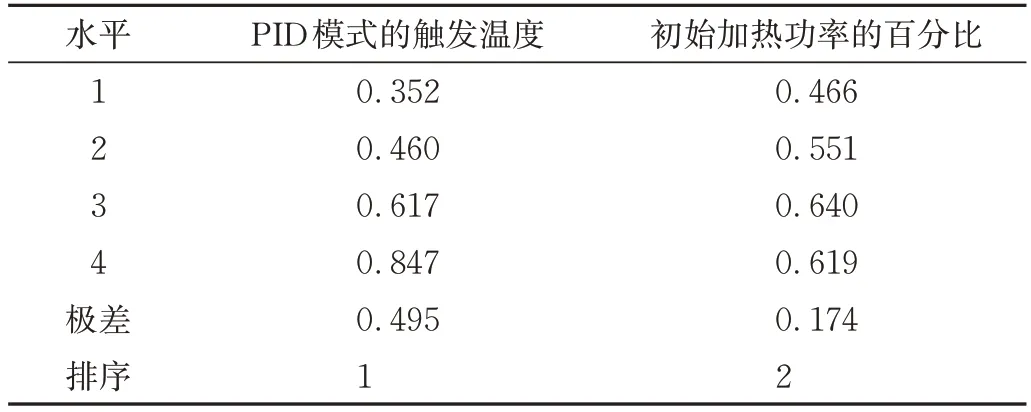
表4 关于加热时间的灰色关联度的极差分析Tab.4 Range analysis of grey relational grade for heating time

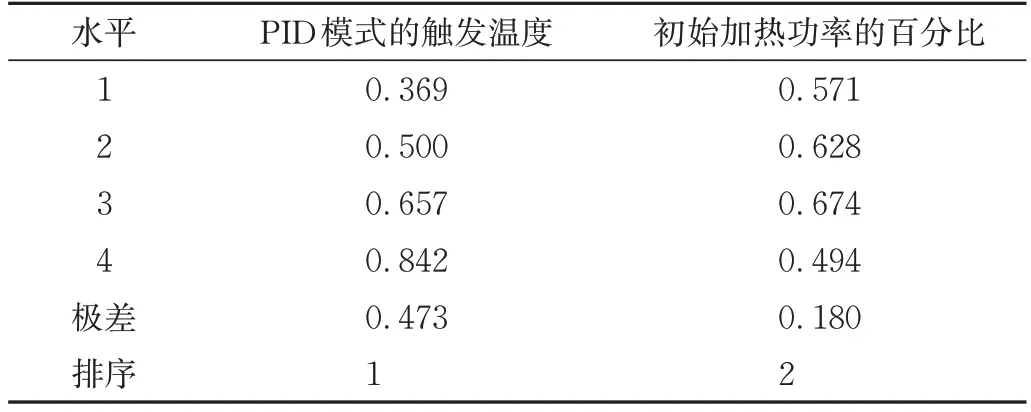
表5 关于加热电能的灰色关联度的极差分析Tab.5 Range analysis of grey relational grade for heating electrical energy

还可以看出，无论是针对加热时间还是加热电能，水平4 的PID 模式的触发温度和水平3 的初始加热功率的百分比都具有最大的灰色关联度平均值，这也从另一个侧面说明最优化的工艺参数为PID 模式的触发温度取250 ℃且初始加热功率的百分比取90 %。

5 结论

（1）在static bed 模型的基础上为制造氢气瓶内胆的电加热滚塑工艺建立了一个传热模型，并通过FLUENT软件来仿真计算在PID控制模式下的模具表面温度和模内温度以及加热时间和加热电能；这些仿真结果与实验结果都吻合得较好，从而验证了本文传热模型的准确性；

（2）停止加热时的模内温度随初始加热功率的百分比变化较小，但随PID 模式的触发温度的升高而降低；

（3）加热时间和加热电能均随PID 模式的触发温度的升高而减少；加热时间先随着初始加热功率的百分比的增大而减少，在除了PID 模式的触发温度为220 ℃之外的情形，加热电能也是先随着该百分比的增大而减少；但当该百分比从90 %增大到100 %时，加热时间略微增加，而加热电能则是急剧增加；最优化的工艺参数是PID 模式的触发温度取250 ℃且初始加热功率的百分比取90 %；

（4）PID 模式的触发温度对加热时间和加热电能的影响程度都要大于初始加热功率的百分比对它们的影响程度。