掺杂B,Cr,Mo,Ti,W,Zr 后金刚石中正电子湮灭寿命计算*

赵永生 阎峰云 刘雪

1) (兰州理工大学,省部共建有色金属先进加工与再利用国家重点实验室,兰州 730060)

2) (兰州工业学院机电工程学院,兰州 730060)

3) (兰州理工大学石油化工学院,兰州 730060)

1 引言

金刚石是一种面心立方结构的碳的同素异形体,常以单质的形式存在于地球深处[1,2],其具有卓越的导热性(≥ 2000 W·m-1·K-1)[3–5]和极低的热膨胀系数(1.18×10–6K)[6],在高功率电子器件、高性能散热器等领域,金刚石常被用作导热垫片、散热器和高温传感器,以提高设备的性能和耐高温能力[7,8].近年来,采用不同的工艺方法,以Al 或Cu 作为金属基体,以金刚石作为增强相,制备出了不同热导率和热膨胀系数的金属基金刚石复合材料[9–12].尽管以金属为基体的金刚石复合材料被广泛研究和应用[13–15],但由于金属与金刚石界面的润湿性较差[16,17],导致金刚石与金属基体之间的微观界面存在不同程度的缺陷,如界面空位、裂纹、镀层脱落、金刚石表面碳化等.为优化金属与金刚石之间的界面性能,一般在制备金属基金刚石复合材料前,都会对金刚石表面进行预处理,引入B[18,19],Cr[20],Mo[21],Ti[22,23],W[24]和Zr[25,26]等元素,以提高金属与金刚石的界面性能.引入以上元素对金刚石表面进行预处理的同时,高温、高压或电离环境均会对金刚石表面造成一定的空位或杂质原子的掺杂.因此,研究掺杂元素引起的金刚石表面微观缺陷,对制备金属基金刚石复合材料具有重要的理论指导意义.本文通过引入正电子湮灭寿命的计算,来研究金刚石中空位和掺杂原子引起的缺陷.

正电子湮灭技术的基本概念: 一个正电子与一个电子湮灭成两个γ–量子.通过测量入射正电子到γ–量子产生的时间,即可计算出正电子的湮灭寿命.对于完美晶格材料而言,由于原子之间的电子密度一致,导致入射正电子很快与电子发生碰撞并湮灭成两个γ–量子.但当晶体中存在空位、掺杂原子等缺陷时,电子密度的改变导致正电子可能被困在空位,从而延长了其湮灭寿命.正电子湮灭寿命与湮灭位点的电子密度成反比,即使掺杂浓度为百万分之一级别的缺陷也可以通过正电子湮灭寿命进行研究[27,28].因此利用正电子湮灭寿命测量技术可以对金刚石的晶格缺陷、空位、掺杂原子和电子结构进行高灵敏性表征[29,30].已有研究报道通过计算天然金刚石和人工合成金刚石中正电子湮灭寿命,成功地揭示出包括空位(单空位、双空位和空位簇)、位错等缺陷[31–34].Fujii 等[35]利用电子湮灭光谱技术测得不同类型人工合成金刚石中正电子的湮灭寿命,其中Ib 型合成金刚石的正电子寿命为115 ps.同时,他们通过双X 射线测量结果显示合成金刚石在微晶或晶界处存在间隙.Marat Eseev 等[36]通过正电子湮灭光谱法研究了金刚石中含杂质N 原子和空位缺陷.综上所述,在金刚石中,正电子的湮灭寿命与材料的缺陷种类和浓度有密切的关系.通过研究正电子的湮灭寿命,可以更好地了解金刚石材料中的缺陷情况.这对于理解金属基金刚石复合材料的界面性能、热传导性能具有重要意义.然而,当前阶段,金刚石表面掺杂元素与金刚石之间的相互作用,导致的正电子湮灭寿命变化尚未得到系统研究.

本文通过利用第一性原理计算方法,对金刚石的完美晶体、单空位、掺杂B,Cr,Mo,Ti,W 和Zr 后的金刚石中正电子湮灭寿命进行计算,并分析影响金刚石中正电子寿命的主要因素.研究内容主要分为三部分: 1) 通过采用不同的正电子湮灭寿命算法和湮灭增强因子,并结合不同的密度泛函,计算了正电子湮灭寿命,同时与文献报道的结果进行对比,以确定最佳的计算方法;2) 对完美金刚石晶体、单空位缺陷下的金刚石正电子湮灭寿命计算;3) 通过对掺杂B,Cr,Mo,Ti,W 和Zr 元素后的金刚石中正电子湮灭寿命的计算,进一步分析影响正电子湮灭寿命的主要因素.

2 计算方法和模型

2.1 计算细节

本文的计算工作基于第一性原理计算软件Abinit[37–41].晶体模型采用VMD 软件进行渲染和可视化[42],电荷密度采用VESTA 软件进行三维可视化[43].采用平面投影叠加波方法(projector augmented wave,PAW)以准确处理电子与离子之间的相互作用.电子–正电子关联势采用Boronski 和Nieminen[44]函数描述,采用随机相位近似(random-phase approximation,RPA)作为增强因子[45].采用广义梯度近似法(GGA-PBE)和局域密度近似(LDA-PW)来描述电子之间的交换和关联作用.计算时自洽循环迭代精度设置为2.72×10–17eV/Bohr,对应的原子精度为10–9eV/atom,正电子能量收敛精度为2.72×10–4eV.对于金刚石、掺杂B,Cr,Mo,Ti,W 和Zr 后平面波的截断能选取,粗网格的截断能分别为408,544,680,953,816,408 和408 eV,精细网格的截断能分别为816,953,953,1225,1225,816 和816 eV.K点网格为4×4×4,计算模型采用2×2×2 超胞.金刚石及其超胞晶体结构弛豫计算采用PBE 泛函,计算正电子湮灭寿命时,使用Broyden-Fletcher-Goldfarb-Shanno (BFGS)方法对掺杂结构进行弛豫处理.

2.2 计算方法

第一性原理计算正电子湮灭的方法主要有两种,分别为直接方法和间接方法.直接方法是将系统能量作为正电子与电子相互作用的势能,在该势场中计算正电子的动力学轨迹,最后通过正电子与电子湮灭的概率计算湮灭速率,从而得到正电子湮灭寿命.间接方法则先将系统的电子结构计算出来,然后利用电子密度来计算正电子湮灭速率.Abinit 实现正电子湮灭寿命的计算方法采用的是双分量密度泛函理论(two-component density functional theory,TCDFT)[46,47].在这种方法中,正电子和电子的自旋被明确的考虑,而正电子和电子的相互作用被纳入在一个有效的湮灭势中.这使得可以采用标准的量子力学方法计算正电子结合能和寿命,而不需要直接求解与正电子-电子湮灭相关的复杂多体问题.利用双分量密度泛函理论计算正电子的湮灭寿命,需要知道系统中正电子密度n+(r) 和电子密度n(r) 的分布,因为它们决定了湮灭的概率.正电子的寿命τ 取决于这个概率,并且可以被视为捕获率λ 的倒数来进行计算,主要的计算公式如下:

其中c表示光速;r0表示电子的经典半径;g(n+,n)表示一个增强因子.正电子和电子密度可以在自洽步骤中使用双分量密度泛函理论来计算.存在涉及不同参数化和近似的多种计算方案,Abinit 选择使用基于Boronski 和Nieminen 的计算方法,并由Puska,Seitsonen 和Nieminen 等实现的参数化.

2.3 结构模型

金刚石结构是一种由两个面心立方点阵沿立方晶胞的体对角线偏移1/4 单位嵌套而成的晶体结构,属于布喇菲点阵(Bravais lattice)中的立方晶系,空间群号为Fd-3m(227 号).金刚石结构中每个碳原子与周围4 个碳原子形成共价键,构成一个三维网络结构,经完全几何优化后,金刚石的晶格参数为3.574 Å,与文献报道的实验测量值3.567 Å[48,49]相比,误差小于0.2%,这表明采用的计算方法可靠,选择的计算参数正确.在计算正电子湮灭寿命时,通过对结构弛豫后的金刚石原胞进行扩胞,扩胞大小为2 × 2 × 2,如图1(a)所示,扩胞后的结构包含64 个碳原子.然后对金刚石超胞做进行空位处理,生成的结构见图1(b),随后对金刚石超胞做空位和掺杂处理,图1(c)为晶体结构.

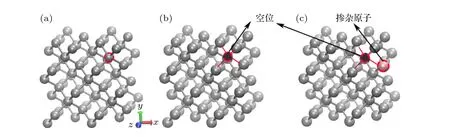
图1 金刚石正电子湮灭寿命计算模型 (a) 2×2×2 的金刚石超胞;(b) 金刚石空位模型;(c) 金刚石空位和掺杂模型Fig.1.Calculation model for positron annihilation lifetime of diamond: (a) Diamond supercell of 2×2×2;(b) diamond vacancy model;(c) diamond vacancy and doping models.

3 结果和分析

3.1 金刚石晶格中的正电子湮灭寿命

在理想金刚石晶格中,由于金刚石具有较宽的能带间隙,约为5 eV[50],导致其核外电子不能像金属中的自由电子一样自由移动,因此金刚石入射正电子的湮灭寿命较短,文献报道主要集中在97—115 ps 之间[31,51,35].造成该结果的原因与金刚石存在缺陷有关,但较低的正电子湮灭寿命值可能预示着金刚石的结构趋于完美.使用不同的赝势文件进行计算将得到不同的正电子湮灭寿命,如表1 所列.通常情况下,采用广义梯度近似(GGA)计算的正电子湮灭寿命普遍比局域密度近似(LDA)的结果大.引起这种现象的主要原因是GGA 和LDA 这两种泛函对于电子行为描述的不同.LDA 主要基于电子的局部密度,而GGA 则考虑了电子密度及其在空间中的变化梯度.通过与实验测量结果比较,对于金刚石完美晶格中的正电子湮灭寿命计算,推荐使用Boronski 和Nieminen 函数作为电子–正电子关联势,并采用RPA 限制作为湮灭增强因子.此时得到的正电子湮灭寿命计算值为99.8 ps,与Uedono 等[51]采用电子辐射手段测量的人工合成的IIa 型金刚石晶体中正电子湮灭平均寿命98.7 ps 相近,同时与Shiryaev 等[52]报道的单晶金刚石中正电子湮灭寿命98 ps 相近.对于金刚石中存在单空位的情况,正电子湮灭寿命有所增加,如Dannefaer 等[53]采用3.5 MeV 电子辐照测量金刚石单空位时的正电子湮灭寿命为120 ps,本文的计算值为119.87 ps.因此,在后续计算过程中,若无特别说明,则选择Boronski 和Nieminen 函数作为电子–正电子关联势,采用RPA 限制作为湮灭增强因子,同时采用局域密度近似泛函对金刚石中正电子湮灭寿命的进行计算.

表1 采用不同正电子–电子交换关联函数和增强因子计算的金刚石正电子湮灭寿命值Table 1.Diamond positron annihilation lifetime values calculated using different positron electron exchange correlation functions and enhancement factors.

3.2 金刚石空位和掺杂缺陷

在完美金刚石晶格中,电子密度呈现出规律性的梯度变化.然而,当存在空位缺陷时,空位处电子密度会急剧降低,如图2(b)所示.在图2(b)中右上部分形状类似于一个“十”字处,C 原子的缺失导致该处C 原子与其最近邻4 个C 原子之间的C—C 共价键缺失,造成此处电子密度显著小于其他位置,同时造成一个空位区间,空位的形状如图2(c)中黄色变形球体.从图2(c)可以明显看出,该空位并非一个标准的四面体,四面体每一个面的中间都存在凹陷,这也与电子密度分布结果(图2(a))相一致.由于正电子与电子之间存在库仑相互作用的现象,电子密度较低的空位会捕获正电子,正电子将“困”在此区域内,就像图2(d)所示的绿色密度区域内.在这种情况下,由于入射正电子不能立刻与C 原子外部的电子结合湮灭并释放γ射线,相应的正电子湮灭寿命会有所增加.

图2 金刚石空位模型及电子密度图 (a) 金刚石空位模型及切面示意图;(b) 金刚石空位切面二维电子密度图;(c) 金刚石正电子模型及切面示意图;(d) 金刚石空位切面二维电子密度图Fig.2.Diamond vacancy model and electron density diagrams: (a) Diamond vacancy model with cross-section;(b) 2D electron density map of the diamond vacancy cross-section;(c) diamond positron model with cross-section;(d) 2D electron density map of the diamond positron cross-section.

实际上,对于以金刚石为增强相的金属基复合材料,对金刚石表面做掺杂处理时,不仅会造成空位缺陷,且由于复合材料制备时一般在高温、高压或电离等环境下进行,一定程度上会造成金刚石表面杂质原子的掺杂现象.此时,金刚石表面异质原子的存在,会对原有的金刚石晶格内部的电子分布产生进一步影响.为考察存在空位和掺杂缺陷下正电子在金刚石内部的湮灭寿命,分别对金刚石进行了B,Cr,Mo,Ti,W 和Zr 的掺杂.由于掺杂原子与金刚石中的C 原子之间相互作用力关系,势必会影响到正电子湮灭寿命的计算准确性.计算结果如图3 所示,正电子空位体积的电荷密度阈值为0.01 eV,即黄色形状的最外壳电子密度为0.01 eV.从图3(a)中可以清楚地看到,计算结果显示了正电子定位在金刚石晶格空位的区域,在这种情况下,由于C 原子与最近邻4 个C 原子的共价键关系,空位区域受到最近邻4 个C 原子的库仑作用力,导致此时正电子定位区域如一个圆球被放置在一个正四面体内部,与正四面体的四个面相接触的球体被压缩.当掺入B,Cr,Mo,Ti,W 和Zr 杂质原子后,金刚石的晶格发生了不同程度的变形,从而导致电子密度重新分布,同时正电子的定位区域也发生了变化.当掺杂B 原子时,正电子定位区域缩小,与无掺杂时的正电子定位区域相比较,球体的变形程度更低.然而,在掺杂Cr 原子后,Cr 与其近邻的3 个C 原子之间产生电荷转移,导致Cr—C 之间共价键的产生,形成了CrC3,此时的正电子定位区域呈现为两个同心球体.内部球体由于Cr原子对于电子的吸引力更大,导致其电子密度较高,而外部球体由于C 原子的电子转移,会形成一个较薄的低电子密度区域.两个同心球体同时存在,既阻止了空位的涨大,又对电子形成更强的排斥作用,因此,Cr 原子的掺杂,对金刚石晶格中的空位大小和电子密度有显著的影响.这一计算结果也与Kršjak 等[54]采用正电子湮灭寿命谱(positron annihilation lifetime spectroscopy,PALS)计算测量的实验结论一致,后续内容将进一步解释Cr 原子的作用机制.在Mo,Ti,W 和Zr 原子的掺杂作用下,正电子定位区域的变化基本一致.

图3 金刚石空位与各异质原子的交互作用 (a) 未掺杂金刚石;(b) 掺杂B;(c) 掺杂Cr;(d) 掺杂Mo;(e) 掺杂Ti;(f) 掺杂W;(g) 掺杂ZrFig.3.Interaction of diamond vacancies with various heteroatoms: (a) Pristine diamond;(b) doped with B;(c) doped with Cr;(d) doped with Mo;(e) doped with Ti;(f) doped with W;(g) doped with Zr.

表2 列出了掺杂B,Cr,Mo,Ti,W 和Zr 原子后,采用广义梯度近似和局域近似密度泛函计算得到的正电子湮灭寿命[53,55].结果显示,使用两种交换关联函数计算的金刚石中正电子湮灭寿命具有较好的一致性.对于掺杂B 和Cr 原子后,金刚石中的正电子湮灭寿命发生了显著变化,分别为146和156 ps.而掺杂Mo,W,Ti 和Zr 原子后,正电子湮灭寿命基本保持在115—118 ps 之间.与金刚石单空位时的119.87 ps 相比较,掺杂B 和Cr 原子后正电子湮灭寿命得到显著增加.然而,根据图3(b)和图3(c)的结果显示,此时正电子湮灭寿命的增加并不能全部归结于空位缺陷对于正电子的捕获因素.由于原子核外电子以近似球形轨道围绕原子核做高速运动,电子密度和电位在这些球体内被近似认为是球形.因此,不同原子由于核外电子排列的不同,其核外电子密度和电位也不近相同.此时,由于正电子–电子相互作用而产生的亲和力应被考虑,尤其是掺杂原子对于正电子的亲和力.这一点对于揭示掺杂原子后的正电子湮灭寿命的变化至关重要,并且可以解释正电子在空位中的扩散情况.

表2 掺杂B,Cr,Mo,Ti,W 和Zr 原子后,金刚石中正电子湮灭寿命值Table 2.Positron annihilation lifetime values in diamond after doping with B,Cr,Mo,Ti,W,and Zr atoms.

为进一步考察金刚石中掺杂原子引起的电子密度的变化,分别对未掺杂原子、掺杂B,Cr,Mo,Ti,W 和Zr 原子后的金刚石电子密度进行计算,如图4 所示.根据表2 计算结果可知,掺杂Cr 原子时,金刚石中正电子湮灭寿命最大,为156.82 ps.首先,可以肯定的是随着正电子湮灭寿命的增加,正电子在空位内的停留时间将会增加,这主要取决于两个因素.一是空位变大,正电子自由移动的空间增加;二是空位不变的情况下,作用在正电子上的力变大,导致正电子滞留时间增加.很明显,掺杂Cr 原子后,由于Cr 的化学势小于0 eV,这就意味着Cr 原子的存在,将会俘获更多的电子,形成电子密度更低的空域,这一结论也与计算结果一致,如图5(c)所示.掺杂Cr 原子后,正电子定位区域有所增加.此时的正电子定位空位形状呈现为一个多层的球体,从最外层到最内层的电子密度变化为由大到小再到大.尤其在中间的深蓝色区域内,电子密度几乎为0.这也与Cr 原子化学势小于0 eV的结论一致,此时Cr 原子展现出对电子更大的俘获能力.同时,考虑到电子密度几乎为0 的情况,意味着正电子很难与电子相结合,导致正电子滞留时间增加,即正电子湮灭寿命增大.因此Cr 原子对正电子的亲和力较小,这一结果也与Puska 等[56]的实验结果一致,其计算的Cr 原子与正电子的亲和力,仅为–2.62 eV,低于同元素周期(Ⅳ)的Ti 原子(–4.06 eV).而对于第Ⅴ周期元素而言,Mo 和Zr 原子的正电子亲和力分别为–1.92 和–3.98 eV,对于第Ⅵ周期元素W 原子而言,其正电子亲和力为–1.31 eV.需要特别注意的是,当金刚石被W和Mo 原子掺杂后,正电子湮灭寿命有所降低,这与Maier 等[57]观察到的实验结果一致.这种情况主要由于W 和Mo 原子的电子化学势较高,分别为0.35 和0 eV[56].高的电子化学势可能导致W和Mo 原子周围有较多的电子.这增加了正电子与电子的湮灭机会,从而降低了正电子的寿命.

图4 金刚石超胞掺杂后的二维电子密度图 (a) 金刚石超胞模型和切面示意;(b) 掺杂B;(c) 掺杂Cr;(d) 掺杂Mo;(e) 未掺杂;(f) 掺杂W;(g) 掺杂Ti;(h) 掺杂ZrFig.4.2D electron density map of diamond supercell after doping: (a) Diamond supercell model and section illustration;(b) doped with B;(c) doped with Cr;(d) doped with Mo;(e) undoped atoms;(f) doped with W;(g) doped with Ti;(h) doped with Zr.

图5 金刚石掺杂后空位的电子局域函数 (a) 金刚石超胞及正电子空位模型;(b) 掺杂B;(c) 掺杂Cr;(d) 掺杂TiFig.5.Electron local function of vacancies after diamond doping: (a) Diamond supercell and positron vacancy model;(b) doped with B;(c) doped with Cr;(d) doped with Ti.

4 结论

本文利用第一性原理计算方法,采用不同的正电子湮灭算法和密度泛函文件,分别计算了完美金刚石、单空位和掺杂原子后的金刚石中正电子湮灭寿命,分析了以上情况下金刚石中正电子湮灭寿命的变化原因,主要结论如下.

1) 采用局域密度近似密度泛函时,基于Boronski &Nieminen1 正电子湮灭寿命算法,结合RPA 限制的湮灭增强因子,得到的正电子湮灭寿命与Kršjak 等[54]的实验结果较为一致.这表明该计算方法对于研究金刚石中正电子湮灭寿命具有较高的可靠性.

2) 在完美金刚石晶格、单空位以及掺杂B,Cr,Mo,Ti,W 和Zr 后(掺原子百分浓度为1.6%),正电子湮灭寿命变化较为显著,尤其以掺杂B 和Cr 原子后,正电子湮灭寿命由119.87 ps 增大为148.57 ps 和156.82 ps.这表明,金刚石中出现空位或掺杂原子缺陷会导致正电子湮灭寿命增加,同时,不同原子的掺杂对正电子湮灭寿命的影响程度不同.

3) 根据对金刚石在空位和掺杂原子区域的电荷密度计算,发现掺杂原子并未引起金刚石晶格的剧烈畸变.然而,掺杂B 和Cr 原子后,正电子湮灭寿命显著增加.主要原因是B 和Cr 原子的正电子亲和力较低,导致正电子在空位滞留时间增加,从而使湮灭寿命增加.

4) 由于W 和Mo 原子的电子化学势较高,导致W 和Mo 原子周围有较多的电子,这增加了正电子与电子的湮灭机会,从而降低了正电子的寿命.

上述结论为制备金属基金刚石复合材料时,对检测和辨识金刚石表面因掺杂处理而造成的界面缺陷提供了重要的理论参考.