初中数学核心问题课堂教学案例——以“三角形”第二课时为例

文| 段金朋

一、教学目标

根据《义务教育数学课程标准（2022 年版）》中有关“三角形”第二课时教学的指示，立足该章节内容所涉及的核心素养，制订如下教学目标，具体如表1 所示。

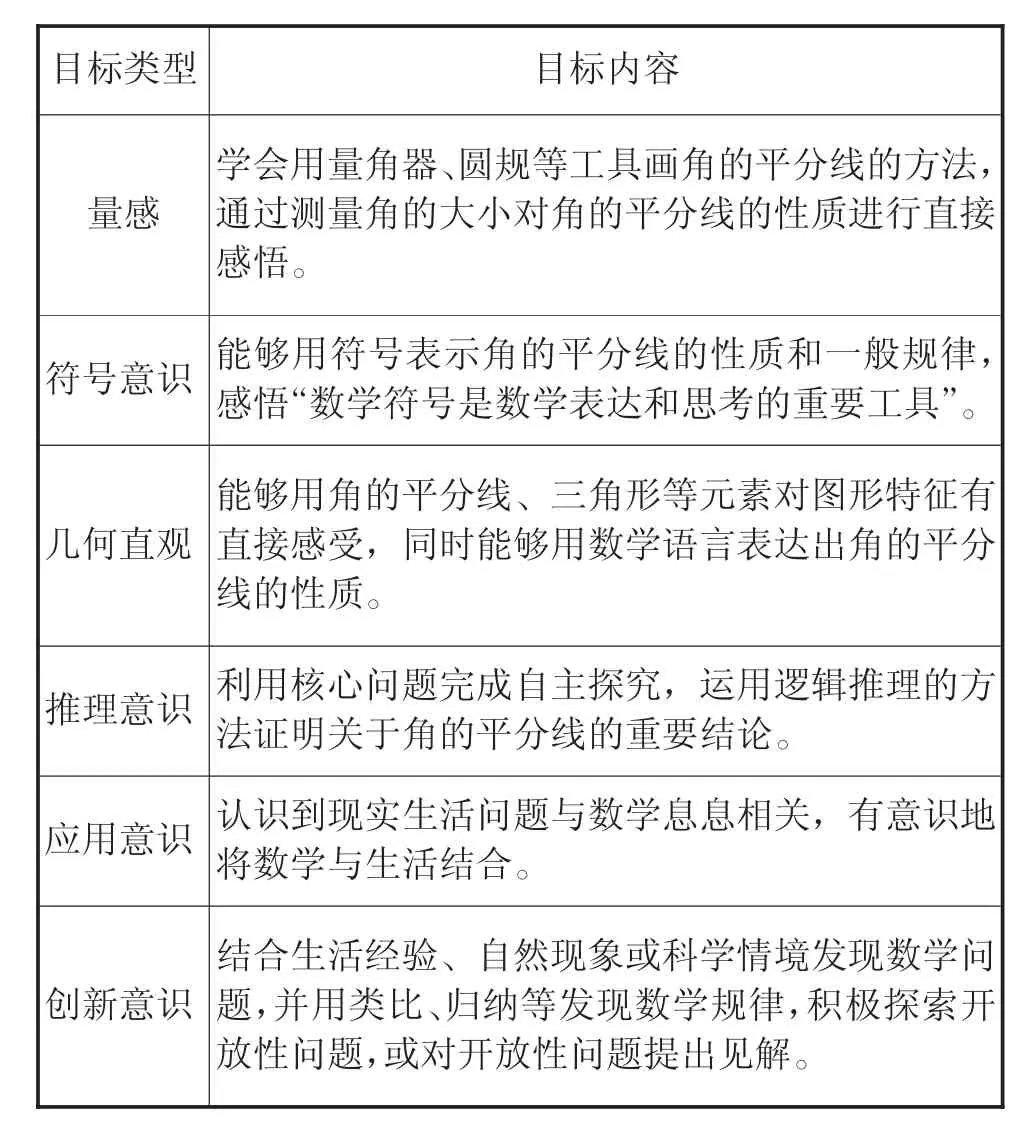
表1

二、教学重难点

（一）教学重点

1.正确了解角平分线性质定理及逆定理。

2.加深对线段垂直平分线和角平分线的性质定理及逆定理的理解，利用定理完成题目解答。

（二）教学难点

1.添加辅助线，构造基本图形。

2.线段垂直平分线、角平分线性质定理及逆定理的综合应用。

三、教学内容分析

该内容可划分为角的平分线1、角的平分线2 两大板块开展教学，第一板块着重带领学生探究角的平分线性质定理及逆定理；第二板块着重带领学生学会用角的平分线性质定理及逆定理完成解题。

四、教学过程

（一）角的平分线1

片段一：

设置核心问题与问题链。（如表2 所示）

表2

教师：（利用多媒体课件展示核心问题）顾名思义，角的平分线除了能够平分角之外还有其他的性质吗？并展示如下例题。

例1：如图1，OC 是∠AOB 的角平分线，在OC上任取一个与O 不重合的点P，完成操作测量：取点P 不同位置，过点P 向OA、OB 作垂线段，即PD⊥OA，PE⊥OB，其中点D、E 为垂足，测量PD 与PE 的长，并完成表3 的填写。观察表格测量结果，猜测PD与PE 的关系，并完成证明。

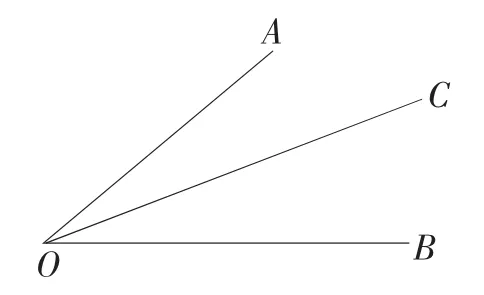
图1

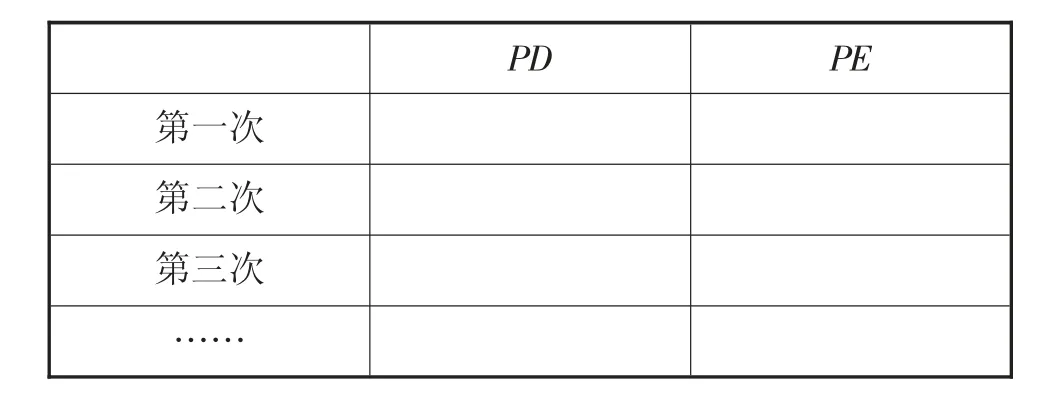
表3

在该活动中，学生利用尺子测量线段长度完成表格记录，发现PD、PE 之间存在相等关系，教师即可引导学生用数学语言总结并鼓励学生上台利用希沃白板画图（如图2），在图中标注出已知条件，并完成证明，如下所示。

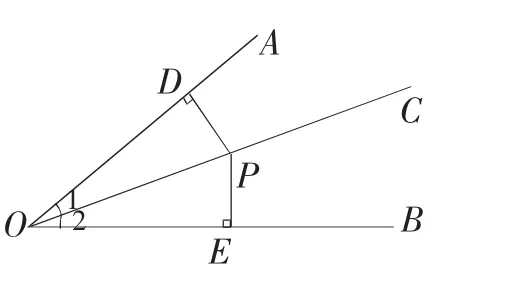
图2

教师：请问哪位同学可以分步骤阐述这位同学的证明步骤？

生B：第一步，OC 是∠AOB 的平分线是题干已知条件；第二步，∠1=∠2 是根据角的平分线定义得出的；第三步，PD⊥OA，PE⊥OB 是题干已知条件；第四步，∠PDO=∠PEO=90°是根据垂直的定义所知；第五步是根据AAS 所得出的结论；最后则是根据小学所学的全等三角形对应边相等所得出的结论。

（设计意图：通过设置核心问题以及以核心问题为导向的问题链引导学生开展探究活动，帮助学生正确、深入地理解角平分线上的点到角两边距离相等，更进一步探究角的平分线性质定理。）

片段二：

完成角的平分线性质定理的教学后，教师可以教学目标为导向设置角的平分线性质定理逆定理的核心问题（如表4 所示）。

表4

以核心问题为导向，教师在课堂中提出问题，学生在学完角的平分线性质定理后能够轻松预设出：到一个角的两边距离相等的点在这个角的平分线上。

在学生的回答下，教师继续追问（如表5 所示）：

表5

在问题的引导下，教师邀请学生上台回答：

生C：到一个角的两边距离相等的点需要在角的内部。

教师：包不包括顶点？

生C：包括！

教师：同学们能否大声完整地叙述一次？

生（全）：在一个角的内部（包括顶点）且到角的两边距离相等的点在这个角的平分线上。

教师：那这个命题是真命题还是伪命题？

生（全）：真命题。

教师：这个逆命题确实是真命题，我们可将这个逆命题称作角的平分线性质定理的逆定理。

（设计意图：在该活动中，教师通过核心问题提出阶梯性问题，类比线段的垂直平分线性质定理的逆定理引出角的平分线性质定理的逆定理，体现出数学思维的阶梯性和递进性。）

（二）角的平分线2

在第二板块的教学中，核心问题如表6 所示：

表6

教师：（多媒体展示课件）请同学们思考例题。

例2：如图3 所示，已知AO 平分∠BAC，CD⊥AB，BE⊥AC，垂足分别为点D、E，且BE 与CD 相交于点O，求证OB=OC。

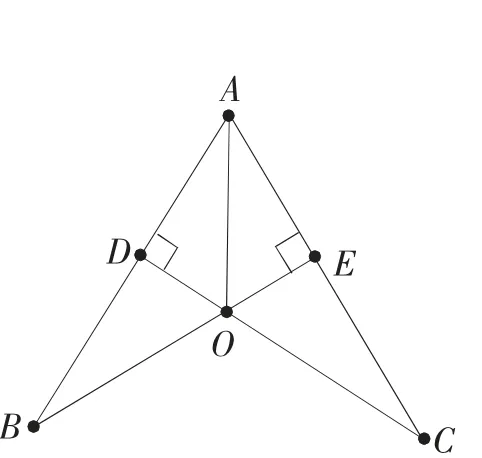
图3

在上述问题中，我并不急于让学生直接完成求证，而是提出下述问题：

（1）AO 平分∠BAC 能够得出怎样的结论？

（2）结合所学的知识，证明两条线段相等的方法有哪些？

（3）结合题干信息，你会选择用怎样的方法证明OB=OC？

在上述问题中，学生利用角平分线定理能够对问题（1）做出回答，即∠BAO=∠CAO，OD=OE；对于问题（2），可结合以往有关三角形的学习，总结出等角对等边、全等、等式性质等证明两条线段相等的方法；而在问题（3）中，根据题干信息，学生能够结合小学全等三角形的知识再结合角平分线性质定理完成证明。

（设计意图：结合题干信息，在问题（1）中能够利用垂直定理，直接利用垂直的意义得到角为90°的结论；在问题（2）中则能够引导学生联系新知和已知，建立数学知识网络；在问题（3）中则培养学生利用知识网络建构解题思路。）

（展示例题）

例3：如图4 所示，CD 垂直平分线段AB，在CD 上取点E，连接EA、EB，求证∠CAE=∠CBE。

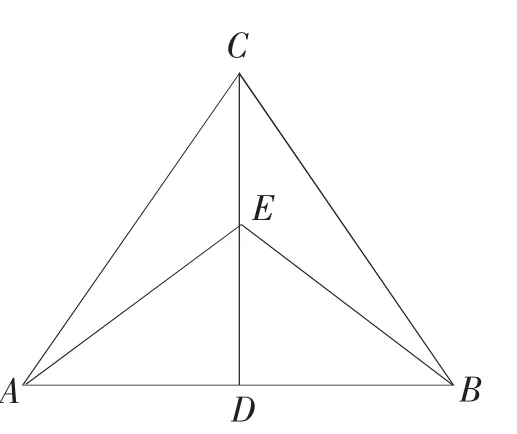
图4

在该例题中，我依旧没有急于让学生完成解题，而是提出核心问题及问题链（如表7 所示）。

表7

教师：有哪位同学能够回答问题（1）？

生A：AD=BD，EA=EB，CA=CB。

教师：你根据什么得出的这个结论？

生A：根据角的平分线定理知道的。

教师：不错！那么哪位同学能够回答问题（2）呢？

生B：等角对等边、全等、等式性质等可以证明两角相等，在这道题中可以利用全等三角形证明两个角相等。

教师：你能否用你的思路上台完成问题（2）的解答？

生B：∵CD 垂直平分线段AB

∴CA=CB，∠CAB=∠CBA，同理得：∠EAB=∠EBA

∴∠CAB-∠EAB=∠CBA-∠EBA

∴∠CAE=∠CBE

教师：有哪位同学能够上台说明这位同学的解题思路呢？

生C：第一步是题干的已知信息；第二步是根据角平分线定理所得；第三步、第四步可以根据等式性质得到。

教师：总结得很棒！这位同学解题思路非常清晰，那么如果我把题干信息简单变化一下，你们还能够完成解答吗？（展示变式训练）

例4：若将点E 移动到CD 延长线上，其他题干信息不变，∠CAE=∠CBE 吗？

在该问题的引导下，学生能够利用垂直平分线定理结合等腰三角形性质证明角相等、线段相等的结论。

（设计意图：在上述例题与变式训练中，教师通过展示垂直平分线的作用引导学生自主探究和证明数学定理，同时通过类比两边相等的方法引导学生熟悉线段垂直平分线性质定理的基本图形。）

五、教学反思

在此次教学实践中，大部分学生均肯定了核心问题在课堂教学中的价值作用，并表示能够促进对数学表象的理解，但是仍有以下需要改进的地方：第一，核心问题设置需要更加关注思维培养和创造生成；第二，情境导入和例题讲解可强化核心问题的作用。从第一点而言，学生的学习水平存在差异性，表现在数学思维的异同、生成性问题提出等方面，所以在设计核心问题时需要仔细分析数学思维培养与创造性、生成性的具体表现，从学生的认知角度构思核心问题；从第二点而言，情境导入和例题讲解是课堂教学的核心环节，核心问题的设计需要基于学生的最近发展区，同时结合学生的生活经验达到以趣激学的目的。