基于k值优化VMD-WT的血糖信号降噪方法研究

吕 生，容芷君，许 莹，但斌斌，代 超，朱潘蕾

（1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北武汉 430081；2.武汉市第五医院，湖北 武汉 430050）

含噪血糖信号影响血糖预测精度[1-2]，故有必要对其进行降噪。商用血糖监测设备[3-5]多是直接滤除信号高频成分进行降噪，但高频成分中可能存在一些有用信号，可将信号按频率高低分解，再对高频成分进行处理实现降噪。目前，已有研究使用经验模态分解(Empirical Mode Decomposition,EMD)进行生理信号降噪[6-9]，而变分模态分解[10](Variational Mode Decomposition,VMD)解决了EMD 及其改进算法的不足，也吸引了学者们的关注[11-13]。基于此，该文提出一种k值优化VMD 结合小波阈值的血糖信号降噪方法，并通过实验验证了此方法的有效性。

1 变分模态分解

VMD 是一种自适应、非递归的时频信号处理方法，该方法认为任何信号都可分解为一系列带宽有限的本征模态的线性组合，将信号处理问题转化为变分模型求解问题，从而实现信号分解。

1）构造变分问题，假设原信号x(t)可被分解为k个模态，为得到k个模态{uk}，使各模态的带宽之和最小且各模态之和等于原信号，其中每个模态均是有带宽限制的调频调幅函数，且每个模态均紧紧围绕在其中心频率附近。首先，利用Hilbert 变换计算各uk(t)的解析信号，得到其单边频谱；然后，通过加入指数项e-jωkt，将模态频谱移到相应的基频带，预先估计模态的中心频率ωk；最后，计算解调信号梯度L2 范数的平方，估计各模态信号带宽，得到变分问题表达式为：

其中，{uk}=(u1,u2,…,uk) 为k个模态；{ωk}=(ω1,ω2,…,ωk)表示k个模态对应的中心频率，∂t表示对t求偏导，δ(t)为冲激函数。

2）变分问题求解，带约束的变分问题往往难以求解，通过引入拉格朗日乘子λ和惩罚因子α，将约束变分问题转变为非约束变分问题，得到式（1）的增广拉格朗日函数：

2 k值优化的变分模态分解

VMD 可自适应地将信号分解为一系列模态信号，但在其使用过程中需要人为设置参数。经研究发现，模态数k对信号的分解效果影响较大。k值偏小则导致欠分解，即信号中所包含的一些本征模态没被完全分解出来；k值偏大则导致过分解，即产生了信号中并不包含的虚假模态。因此，采用VMD 对信号进行分解前，需要确定合理模态分解数目k。该文考虑VMD分解信号得到的残差r(t)，VMD要求分解的各模态之和等于原信号，但求解时只能得到逼近真实解的近似解，故VMD 分解后原信号与各模态之和间存在残差。欠分解时，残差信号中包含着信号中没被分解出来的一些本征模态，残差量较大；k达到合适值时，VMD 可将信号中的本征模态完全分解出来，此时残差量较小，残差信号与原信号的相关性也较小；k超过合适值后，过分解的模态是在本征模态基础上分解出来的，也是由近似解得到的，故使得残差量变大，残差与原信号的相关性也变大。基于此，该文提出了一种基于相关性确定VMD参数k的优化方法。

残差信号公式为：

皮尔逊相关系数计算公式如下：

式中，xi和ri分别为原始信号x(t)和残差信号r(t)中的第i个元素，和分别为x(t)和r(t)中元素的平均值，N为样本数。

基本运算步骤：取不同k值对信号进行VMD 预分解，其他参数取标准VMD 默认值，分解之后分别计算残差信号与信号的相关系数p，观察一系列k值对应的p值，当p值经过几个较低值后出现突变时，则此拐点对应的k就是最优值。

3 基于VMD-WT的降噪方法

3.1 降噪方法

含噪信号经VMD 分解后，可获得一系列从低频到高频排列的模态。血糖信号中的随机噪声主要分布在高频模态中，以往的血糖降噪方法多是通过滤波器直接去除高频成分，而这也可能去除了一些高频有用信息。小波阈值（Wavelet Threshold,WT）[14]不仅能有效滤除噪声，还能保证有用信号不丢失。因此，该文采用k值优化的VMD 联合小波阈值对血糖信号进行降噪，具体步骤如下：1）使用k值优化的VMD 对含噪血糖信号进行分解，得到一组频率不同的模态；2）对高频模态进行小波阈值去噪；3）将降噪高频模态与其余模态进行重构，获得降噪血糖信号。

3.2 降噪效果评价指标

为了量化血糖信号降噪方法的效果，该文分别选取信噪比(Signal Noise Ratio，SNR)、基于降噪血糖预测的MAPE 和克拉克误差网格分析[15]作为降噪效果的评价指标。

信噪比计算公式如下：

式中，x(t)和y(t)分别是原始血糖信号和降噪血糖信号，N是样本数。

MAPE 计算公式为：

式中，N为样本数，yi第i个降噪血糖值，为第i个降噪血糖预测值。

4 血糖信号实例分析

该文数据源于武汉某三甲医院美奇连续血糖监测仪，数据集由每3 分钟采集一次的血糖值组成。选取10 位糖尿病患者数据，某患者连续5 日的血糖变化曲线如图1 所示。

图1 某患者连续5日血糖变化曲线

以该患者血糖信号为例，取k=2～10 分别对其进行VMD 预分解，残差信号与血糖信号的相关系数变化曲线如图2 所示。

图2 相关系数随k值变化曲线

当k=7 时，相关系数取得最小值0.114 3，故将7作为该文的VMD 最优模态分解数目，依此设置参数，其他参数取VMD 默认值。如图3 所示，VMD 分解血糖信号得到的七个模态由低频到高频排列。

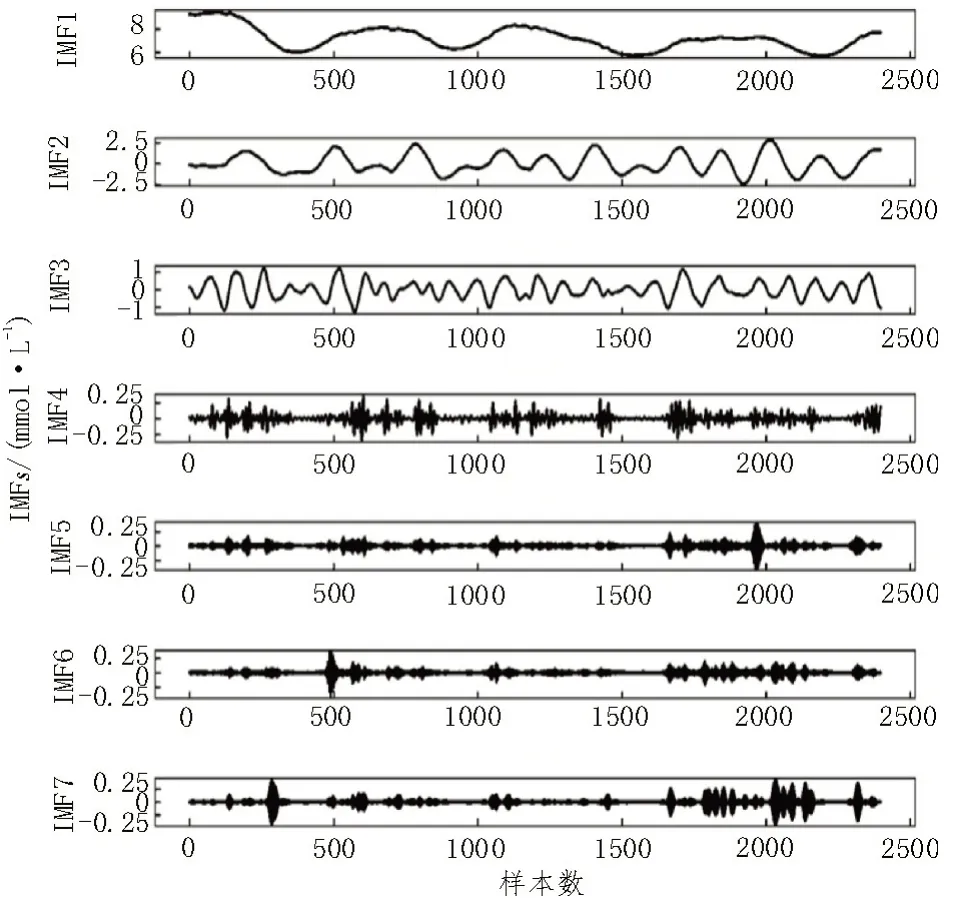
图3 VMD分解结果

对高频模态IMF4-IMF7 进行小波阈值去噪，将降噪高频模态与其余模态重构得到降噪血糖信号。

为了探究该文方法的降噪效果，将其与EMD法、未降噪血糖信号进行对比。如图4 所示，EMD 分解血糖信号得到的模态由高频到低频排列，对高频模态IMF1-IMF3 进行小波阈值去噪。

图4 EMD分解结果

分别计算EMD 法和VMD 法降噪后信号的信噪比，计算结果如表1 所示。

表1 两种方法的降噪效果

由表1 数据可知，VMD 法与EMD 法相比，十位患者血糖信号的信噪比平均提高1.834 6 dB。

分别构建基于VMD 法、EMD 法、未降噪信号的门控循环网络(Gated Recurrent Unit,GRU)[16]预测模型，三种方法的GRU 结构和参数相同，得到的平均绝对百分误差如表2 所示。

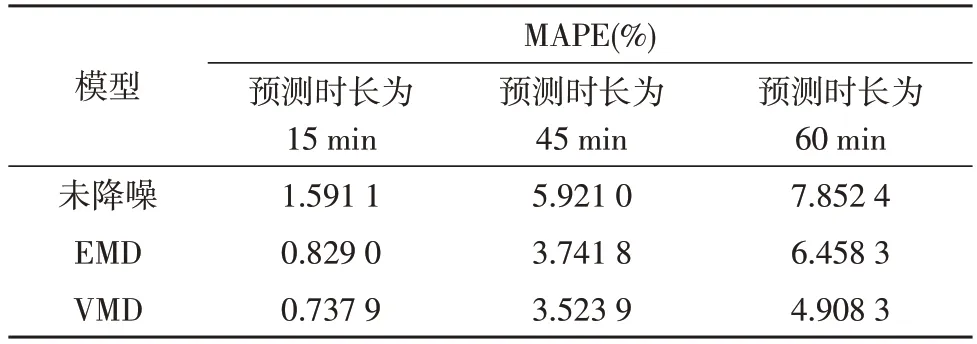
表2 不同方法预测误差比较

预测时长为60 min 时，未降噪信号的预测误差为7.852 4%，EMD 法的预测误差为6.458 3%，VMD法的预测误差为4.908 3%。

克拉克误差网格分析是一种评估血糖预测精确性的方法，区域A 表示预测值偏离实际值不超过20%，具有较高的预测精度，可依此做出正确临床治疗方案。三种方法未来60 min血糖变化的克拉克误差网格分析结果如图5 所示，使用VMD 法预测时[17-19]，A 区域占比97.468 4%；使用EMD 法预测时，A 区域占比93.108 3%；使用未降噪信号预测时，A 区域占比90.258 4%。

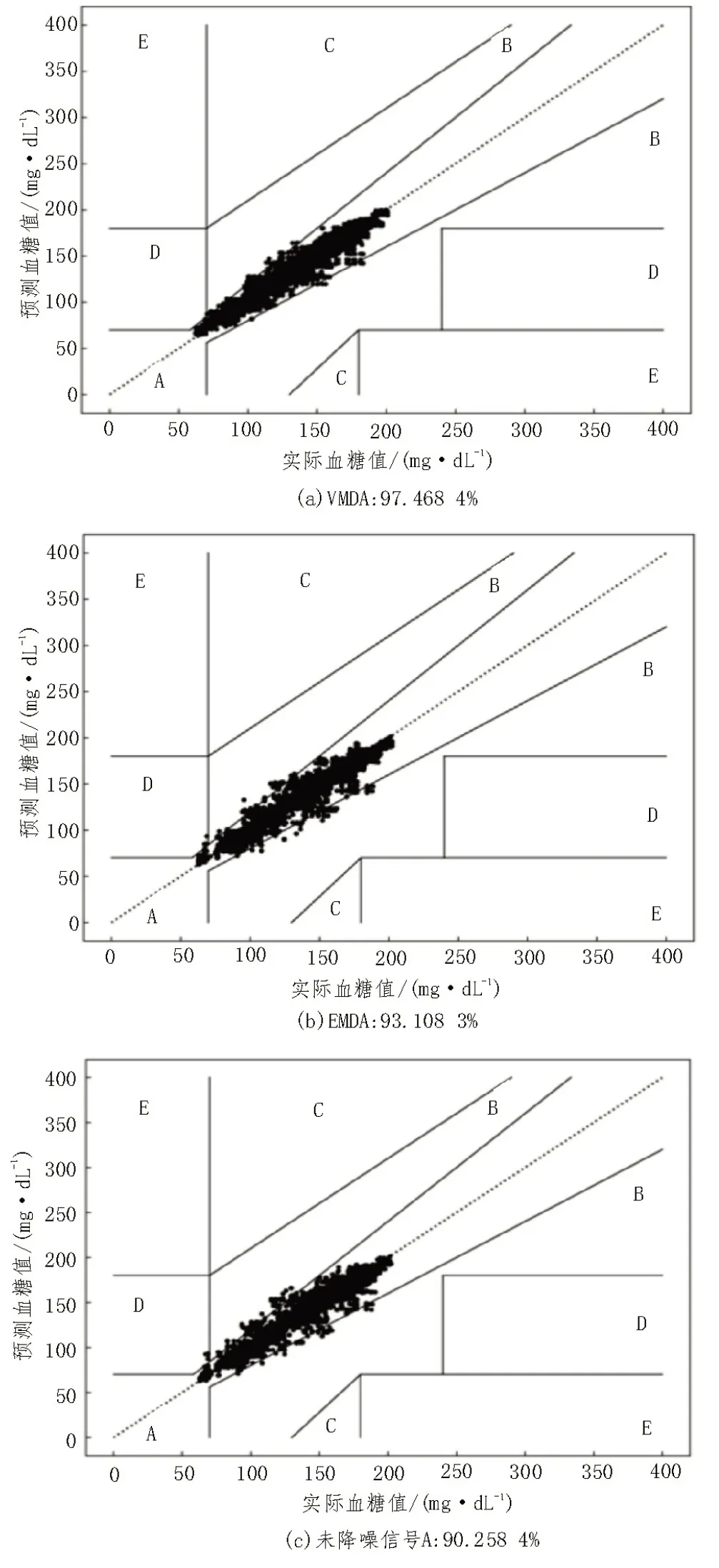
图5 不同方法的克拉克误差分析

5 结论

针对含噪血糖信号影响血糖预测精度的问题，利用变分模态分解及小波阈值对血糖信号降噪进行了研究，得出以下结论：

1）基于血糖信号与残差信号之间相关性的模态选取原则，可确定VMD 最优模态分解数目，使得血糖信号能够被有效分解。

2）k值优化VMD 结合小波阈值对血糖信号进行处理，可有效降低噪声。与EMD 法、未降噪信号相比，该文方法信噪比更高，血糖提前60 min 预测的MAPE 和克拉克误差网格分析结果也更优。