基于解码转发CR-NOMA协同系统物理层安全性能分析*

吕 铄,嵇建波

(1.桂林电子科技大学 电子工程与自动化学院,广西 桂林 541004;2.桂林航天工业学院 电子信息与自动化学院,广西 桂林 541004)

0 引 言

随着5G移动通信技术的发展,物联网、车联网和机器通信得到了广泛的关注。在上述通信网络中,高频谱利用率、支持海量连接、覆盖范围广、时延低是基本要求[1-3]。非正交多址接入(Non-orthogonal Multiple Access,NOMA)和认知无线电(Cognitive Radio,CR)由于能够实现海量连接,提供更高的传输速率和频谱利用率,被公认为5G无线网络中两种重要使能技术[4-5]。NOMA的关键思想是通过利用功率域多路复用、叠加编码和连续干扰消除(Successive Interference Cancellation,SIC)技术,实现一个资源块内多个用户之间的频谱共享。传统静态频谱利用方式下,分配给主用户的许可频谱被禁止用于次用户,CR技术则允许次用户接入许可频谱,可以极大提高频谱利用率[6-8]。一些研究将CR和NOMA结合,以减少干扰,更好地利用频谱资源。例如,Zhang等人[9]将NOMA应用于大规模频谱共享CR网络,通过设计用户的通信速率和功率分配因子,发现在频谱CR网络中NOMA性能优于正交多址技术。

在一些场景中,由于远距离或障碍物,导致源和目的地之间的直接链路可能无法实现,因此中继协作的CR-NOMA网络最近引起了人们的广泛关注[10-12]。张智靓等人[13]假设主用户的干扰是一个常数,推导了协作CR-NOMA的连接中断概率(Connection Outage Probability,COP)和遍历容量,但在实际中这是不现实的。Nguany等人[14]提出一种单中继的协作CR-NOMA网络,信道条件较好的用户具有其他用户的先验信息,信道条件较好的用户对较差用户的消息进行解码转发。然而,由于射频信号的广播性,无线网络中的信息很容易被窃听,传统的加密技术已不能满足无线通信的安全需求。

物理层安全(Physical Layer Security,PLS)技术是从信息论的基本原理出发,利用无线信道的多径衰落和传播时延等物理特性实现安全通信,从而增强无线网络的安全性[15-16]。Zhu等人[17]使用瑞利信道下中继协作CR-NOMA系统模型,应用解码转发策略,推导了次用户的安全中断概率(Secrecy Outage Probability,SOP)表达式,但未得到精确闭合表达式,不便于分析系统参数对安全性能的影响。Zheng等人[18]研究了CR-NOMA系统的物理层安全性能,假设窃听者具有强大的多用户检测能力,这实际上是高估了窃听者的能力,同时并没有得到SOP的精确闭合表达式,不能直观揭示系统参数对物理层安全性能的影响。Singh等人[19]研究了不完全Nakagami-m衰落信道下中继协作CR-NOMA系统的次用户SOP的封闭和广义解析表达式,但没有考虑主用户服务质量约束。Chen等人[20]基于瑞利衰落信道推导了协作CR-NOMA系统SOP的闭合表达式,但同样高估了窃听者的能力,并且没有考虑主用户服务质量约束。Chen等人[21]推导了协作CR-NOMA系统SOP性能,但是没有考虑系统参数对物理层安全性能的影响。

在以上研究工作的基础上,本文分析了Nakagami-m衰落信道下基于解码转发CR-NOMA协同系统的物理层安全性能,考虑了主用户服务质量约束和窃听者的实际信号处理能力,推导出COP和SOP精确闭合表达式和渐近表达式,更加直观地分析出干扰温度、衰落系数、信道增益参数、信号功率分配因子等参数对安全性能的影响。

1 系统模型

如图1所示,考虑一个频谱共享CR系统,该系统由一个次用户发射机(SBS),一个主用户(Pu),两个次用户(Bob1和Bob2)和一个窃听者(Eve)组成。在该系统中,SBS和Bob2没有直接通路,Bob1作为中继节点转发Bob2的信号,中继节点采用解码转发协议(Decode-and-Forward,DF)。假设每个节点拥有一根天线,工作为半双工模式。SBS根据NOMA原理把信号传输给次用户Bob1和Bob2。因为Bob1比Bob2离SBS近些,信道质量比Bob2优越些,所以Bob2比Bob1具有传输优先级。Bob2和Bob1都执行NOMA协议,假设α1和α2分别是Bob1和Bob2功率分配因子,并且它们功率分配系数满足以下条件:α2>α1,α1+α2=1。

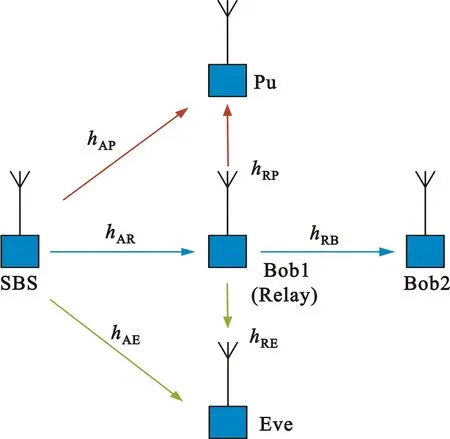
图1 系统模型Fig.1 System model

2 安全性能分析

2.1 信道模型及传输策略

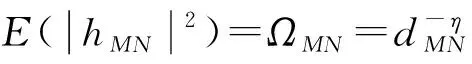
(1)

(2)

同时,窃听者Eve按照次用户Bob1和Bob2处理信号协议,则Eve处x1的SNR和x2的SINR分别为

(3)

第二时隙,Bob1采用DF协议重新编码解调信息x2并将其发送给Bob2,则Bob2接收信号为

(4)

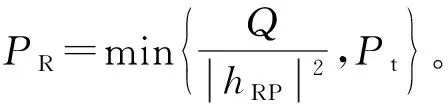
(5)

2.2 安全性能分析

2.2.1 连接中断概率分析

COP是指主信道信息传输速率高于信道容量的概率,作为衡量系统可靠性能指标之一。下面分别推导Bob1和Bob2的COP。

2.2.1.1 Bob1解码x1的COP

Bob1如果在第一时隙未能正确解码信号x2或x1,Bob1都将会发生中断。根据香农信道容量公式,Bob1解码x1时COP表达式如下:

(6)

式中:变量R1和R2分别表示x1和x2的信息传输速率。为了获得Bob1解码x1时COP,首先需要获得γB1,1和γB1,2的累积分布函数(Cumulative Distribution Function,CDF)。对于任一节点M和N之间的信道hMN服从参数为mMN的Nakagami-m (mMN,ΩMN)分布,它的信道增益|hMN|2服从Gamma(k,Ψ)分布,它们参数之间的关系为k=mMN,Ψ=ΩMN/mMN。为了方便计算和理解参数对性能的影响,假设mMN为正整数。

定理1：在Nakagami-m信道下,CR-NOMA系统中Bob1采用DF协议的COP为

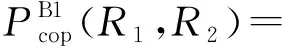
(7)

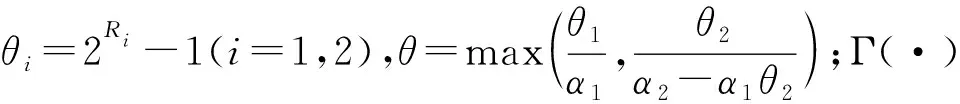
证明:根据式(2)可知,Bob1处x1的SNRγB1,1和x2的SINRγB1,2的CDF分别为

(8)

(9)

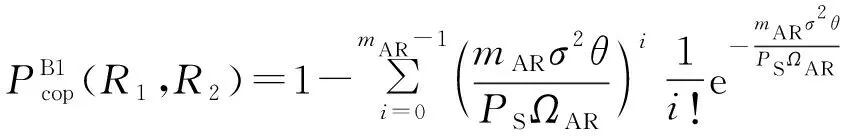
(10)

推论1：当mAR=1和mAP=1时,则信道参数hAR和hAP变为服从瑞利分布,其信道增益|hAR|2和|hAP|2服从独立指数分布。根据非完全伽玛函数Γ(1,x)=e-x,Υ(1,x)=1-e-x,则式(7)简化为

(11)

从推论1可以得到Bob1瑞利信道下的COP闭合表达式。

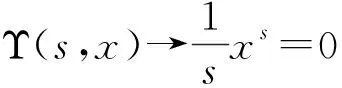
(12)

从推论2可知,当Pt≫Q时,Bob1的COP与Pt无关。当mAR=1和mAP=1时,式(12)可进一步简化为

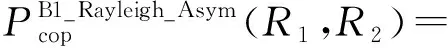
(13)

2.2.1.2 Bob2解码x2的COP

Bob2发生连接中断存在两种情况:第一种情况是Bob1对信息x2不能够正确解码;第二种情况是Bob1对信号x2能够正确解码但Bob2对信息x2不能够正确解码。

定理 2：在 Nakagami-m 衰落信道下,当Bob1采用DF协议转发x2时Bob2的COP为

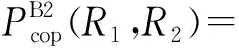
(14)

证明:当Bob1采用DF协议转发x2时,Bob2处信号x2的SINR为

γB2=min{γB1,2,γB2,2}

(15)

根据Shannon信道容量公式,Bob2解码x2的COP为

(16)

类似前面的推导分析,首先需要推导变量γB2的CDF,然后推导出Bob2的条件COP,最后求出Bob2的COP。根据极值定理,根据式(15)可得γB2的CDF为

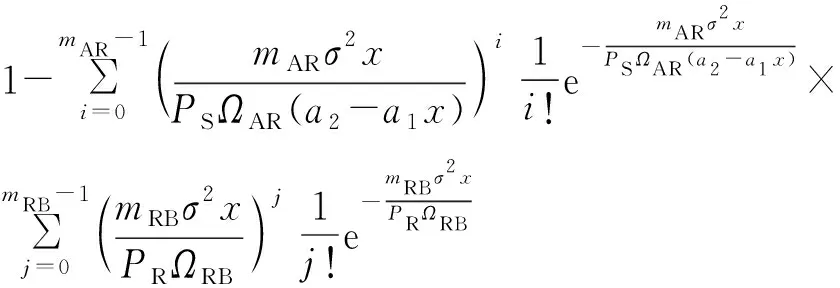
(17)

类似定理1的推导过程,Bob2解码信号x2的COP为式(14)。

推论3：当SBS的峰值发射功率Pt≫Q时,Bob2解码信号x2时的COP渐近表达式为

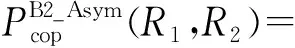
(18)

从推论3可知,当Pt≫Q时,Bob2解码信号x2时的COP与Pt无关。当mAP=mRP=mRB=1时,式(18)进一步简化为

(19)

由式(19),如果α2=α1θ2,则Bob2发生完全中断。

2.2.2 安全中断概率分析

接着下来分析Bob1解码信息x1的SOP。假设窃听者是被动窃听者,由于截获了消息x2,Eve应该首先通过SIC消除来自x2的干扰。根据Shannan信道容量公式,Bob1将信息x1解码时的SOP为

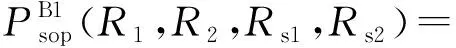
(20)

式中:变量Rs1和Rs2分别表示x1和x2传输安全速率。根据式(20),可以得到Bob1的SOP。

定理 3：在 Nakagami-m 衰落信道下,Bob1的SOP为

(21)

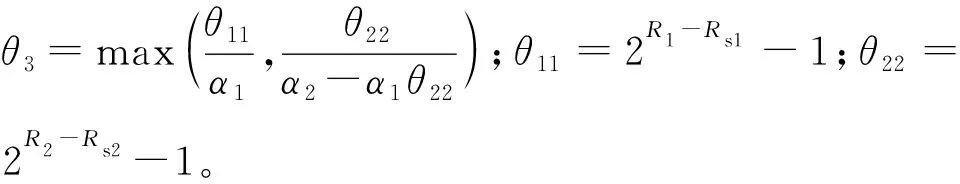
证明:在Nakagami-m 衰落信道下,Eve接收信号x1的SNRγE1,1和x2的SINRγE1,2的CDF分别为

(22)

(23)

综合式(20)、(22)和(23),类似前面的推导,可得到Bob1的SOP为式(21)。

推论4：根据非完全伽玛函数渐近性质,当SBS的峰值发射功率Pt≫Q时,Bob1解码信号x1时的SOP渐近表达式为

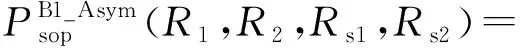
(24)

除满足Pt≫Q外,当mAP=mAE=1时,式(24)可进一步简化为

(25)

定理 4：在 Nakagami-m 衰落信道下,Bob2的SOP为

(26)

证明:对于x2,窃听者Eve工作在两个时隙,选择最好的SNR。Bob2解码x2SNR为

γE2=max{γE1,2,γE2,2}

(27)

根据Shannon信道容量公式,Bob2解码x2时的SOP为

(28)

下面推导γE2的CDF。Bob2 信噪比γE2,2的CDF表达式为

(29)

由式(23)、(27)和(29)可得

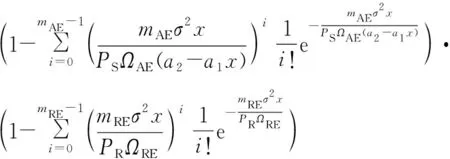
(30)

类似前面的推导,Bob2解码x2的SOP为式(26)。

推论5:当SBS的峰值发射功率Pt≫Q时,Bob2解码信号x2时的SOP渐近表达式为

(31)

除满足Pt≫Q外,当mAP=mRP=mAE=mRE=1时,式(31)可进一步简化为

(32)

3 仿真与分析

本节通过蒙特卡罗(Monte Carlo)仿真来验证上述数值分析结果的正确性,并分析系统参数对安全性能指标的影响。除非特殊说明,设定功率分配因子α1=0.2,α2=0.8;信道参数mAR=mAP=mAE=mRE=mRP=mRB=m=2,信道功率增益ΩAR=0.5,ΩAP=0.5,ΩAE=0.4,ΩRE=0.2,ΩRP=0.5,ΩRB=0.1;干扰温度Q=30 dBm;噪声功率σ2=0.01 W。假设次用户信息传输速率R1=1 b/s,R2=0.5 b/s。仿真中Re1表示R1-Rs1,Re2表示R2-Rs2。

图2与图3分别给出了次用户COP、SOP与SBS峰值功率、次用户信息传输速率、安全传输速率的关系。从图2和图3中可得出以下结论:①数值分析和蒙特卡罗仿真结果非常吻合,验证了理论分析的正确性;②次用户COP随着SBS发射功率的增大而减小,而次用户SOP逐渐变大(这是因为SBS发射功率增大使得次用户Bob1和Bob2能提高接收信号的信噪比,因而COP减小;另一方面,SBS发射功率增大,窃听者Eve截获私密信息概率增加,因此SOP变大);③次用户COP随着其信息传输速率增加而变大,连接可靠性变差(这是因为次用户信息传输速率增加后,次用户所需的信号功率也随之变大);④当Pt≫Q时,Bob1和Bob2的COP最终趋于常数,此时COP与Pt无关,只与干扰温度、功率分配因子和信道增益参数有关,验证了推论2和推论3的分析正确性;⑤SBS峰值功率不断增大,SOP随着次用户安全传输速率增加而变小,安全可靠性变好,意味着系统的可靠性和安全性是相互矛盾的,两者不能同时兼顾。

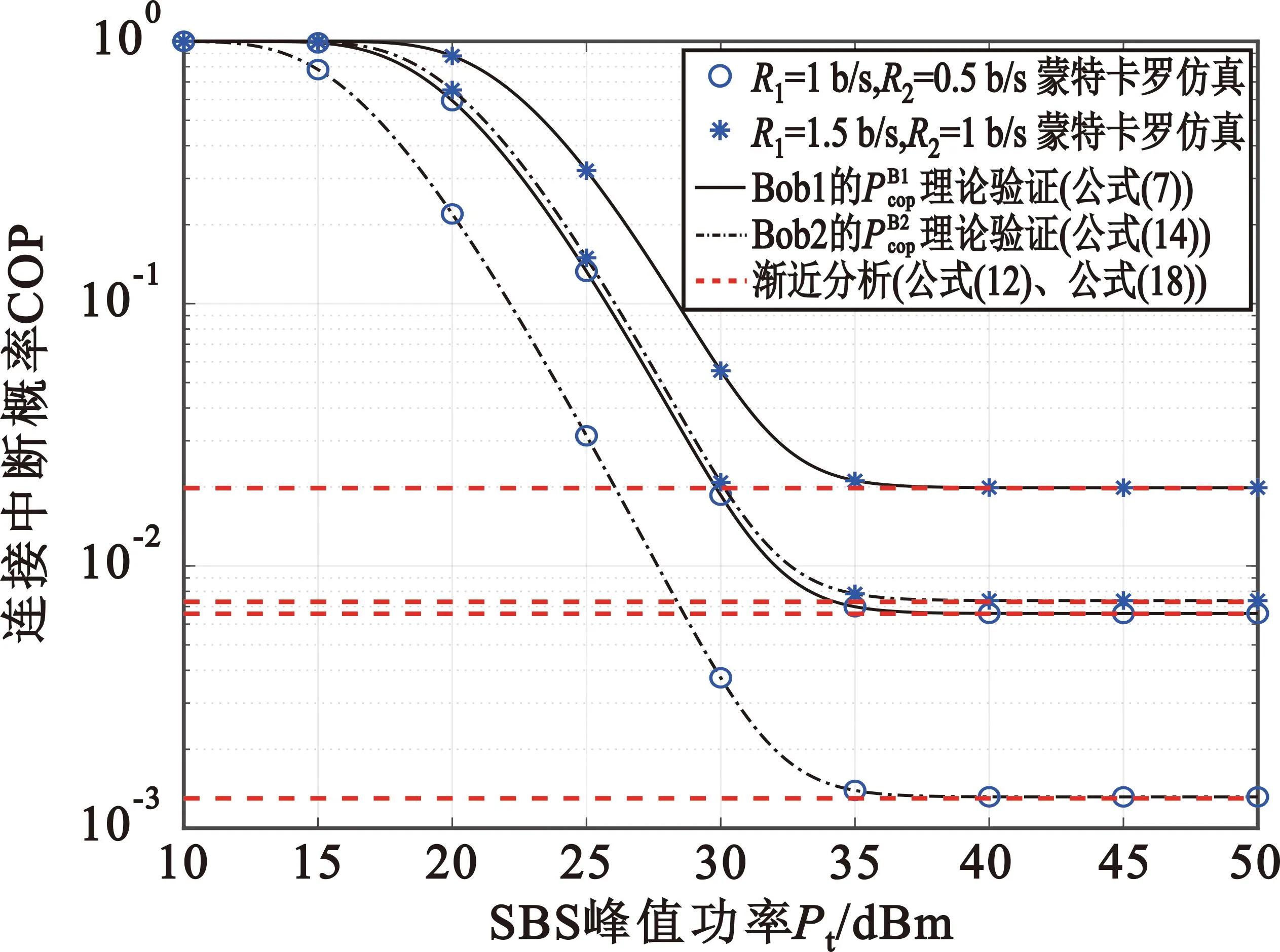
图2 次用户连接中断概率COP与SBS峰值功率、次用户信息传输速率的关系Fig.2 Relationship between COP of secondary users and various peak power of the SBS and information communication rates

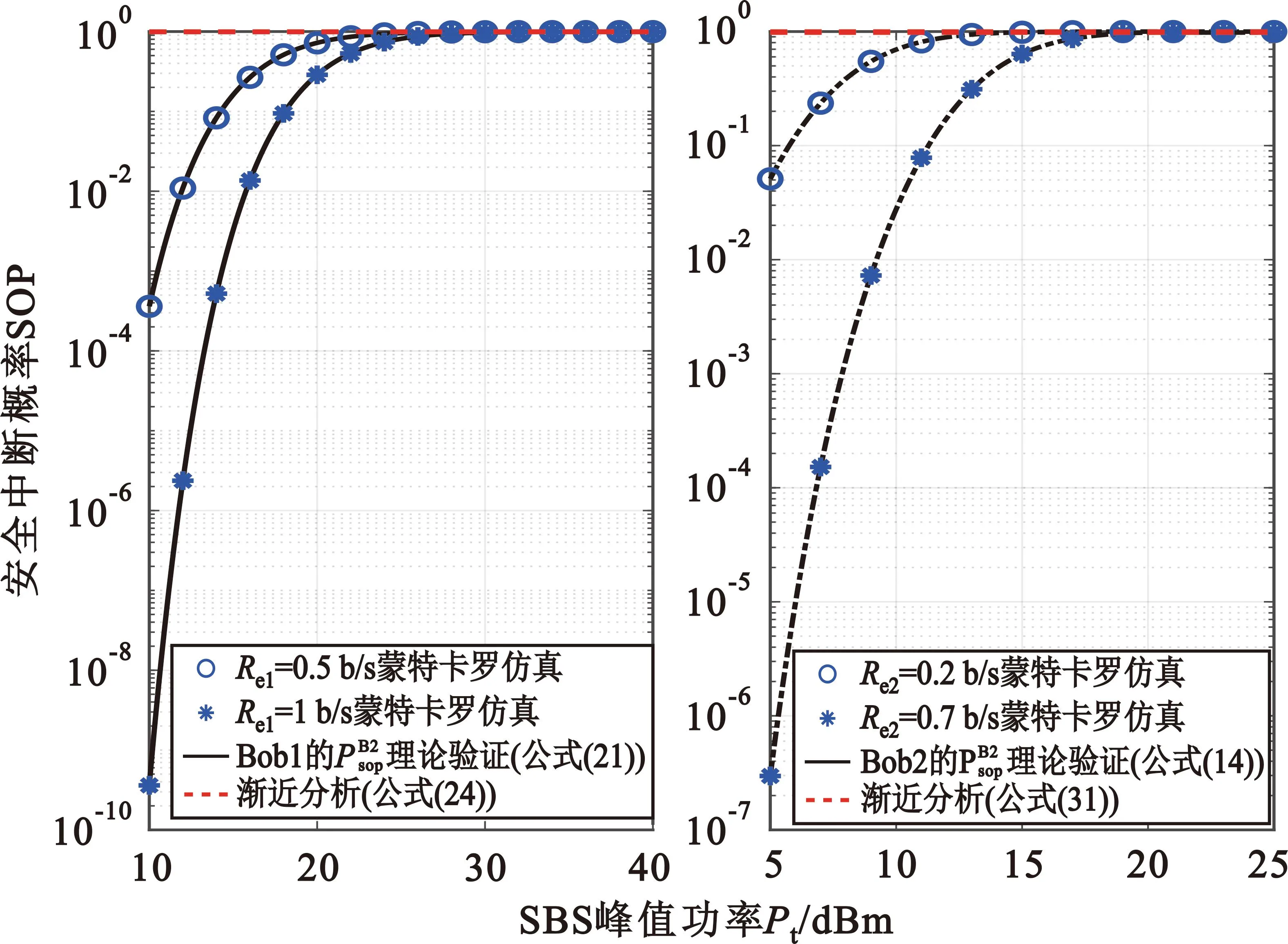
图3 次用户安全中断概率SOP与SBS峰值功率、次用户安全传输速率的关系Fig.3 Relationship between SOP of secondary users and various peak power of the SBS and secrecy communication rates

图4和图5给出了次用户COP、SOP与SBS峰值功率、干扰温度的关系,可以看出:①SBS峰值功率增大时,COP不断减小,SOP不断增大;②由于SBS发射功率受约束,COP与SOP最终趋于稳定值;③SBS峰值功率固定时,次用户的COP随着干扰温度Q值增加而减小,SOP随着干扰温度Q值增加而变大(这是因为Q值增加意味着SBS发射功率可增加,次用户和Eve接收信号SINR(SNR)也随即变大,从而连接中断性能变好,安全中断性能变差),渐近分析曲线进一步验证了该结论。

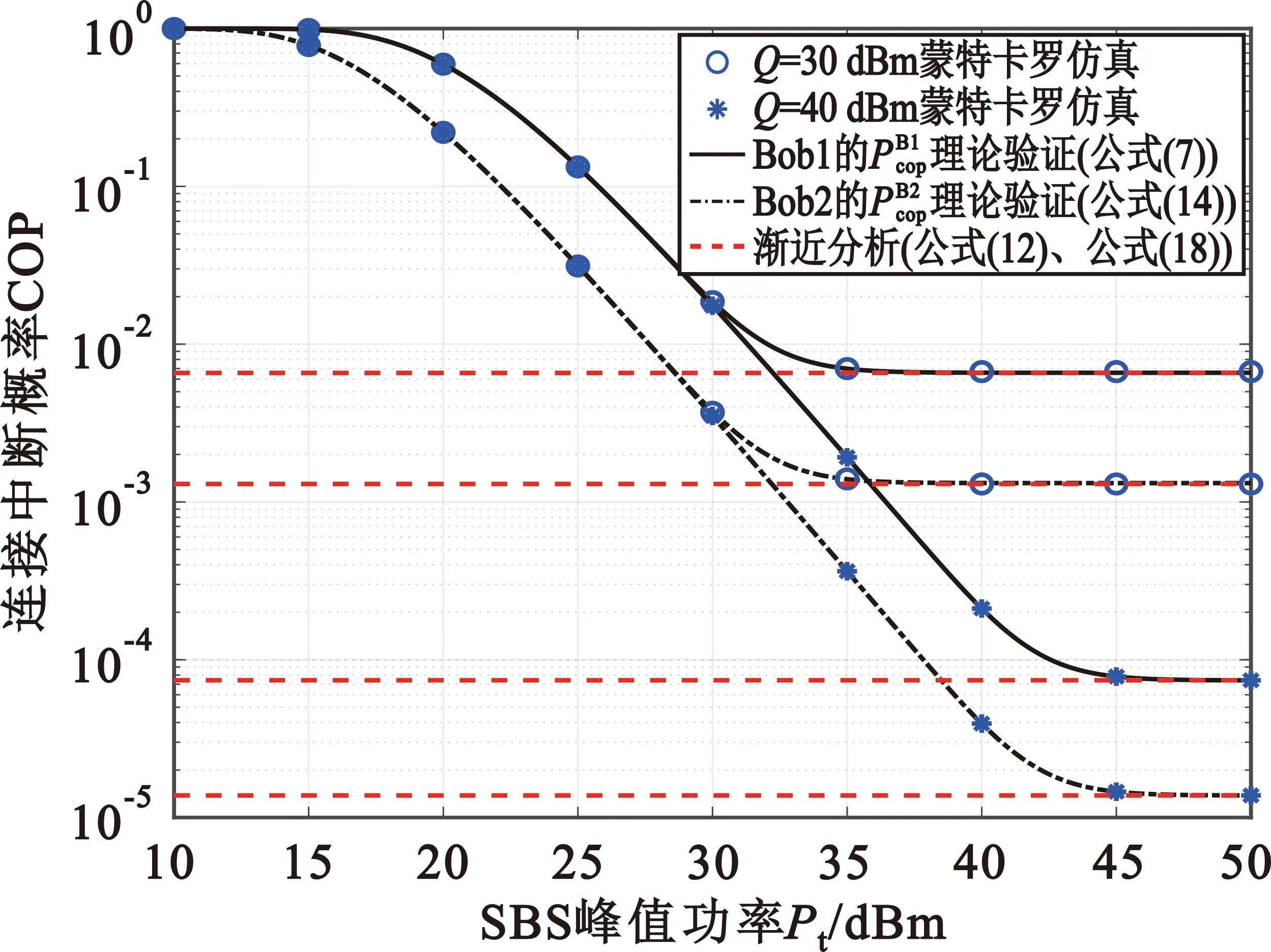
图4 次用户连接中断概率COP与SBS峰值功率、干扰温度的关系Fig.4 Relationship between COP of secondary users and various peak power of the SBS and interference temperature

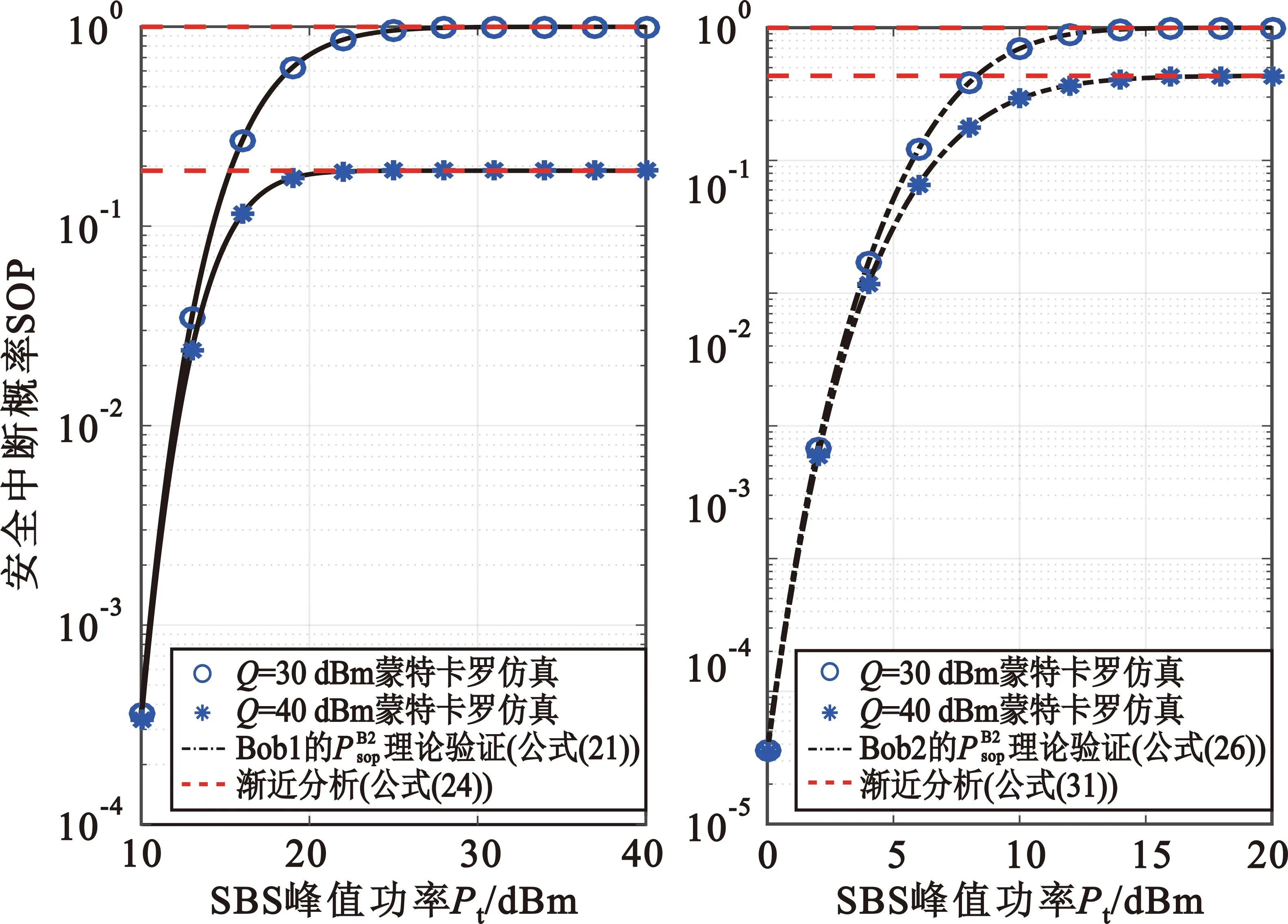
图5 次用户安全中断概率SOP与SBS峰值功率、干扰温度的关系Fig.5 Relationship between SOP of secondary users and various peak power of the SBS and interference temperature

图6和图7给出了次用户COP、SOP与信道参数m的关系。从图6和图7中可得出以下结论:①SBS峰值功率固定时,m越大,次用户COP越小,连接可靠性越好;②对Bob1,SBS峰值功率在10～15 dBm的区间内,Bob1在m=1(瑞利)信道下的SOP远小于m=2信道和m=3信道,安全可靠性表现突出;SBS峰值功率在15～40 dBm区间时,Bob1在信道参数m=3信道下的SOP最小,但与瑞利信道和Nakagami-m信道相比安全可靠性差距不明显;③对Bob2,SBS峰值功率在5～13 dBm区间内,Bob2在瑞利信道下的安全可靠性表现突出;SBS峰值功率在15～40 dBm区间时,Bob2在信道参数m=3信道下的安全可靠性比其他两个信道稍好。

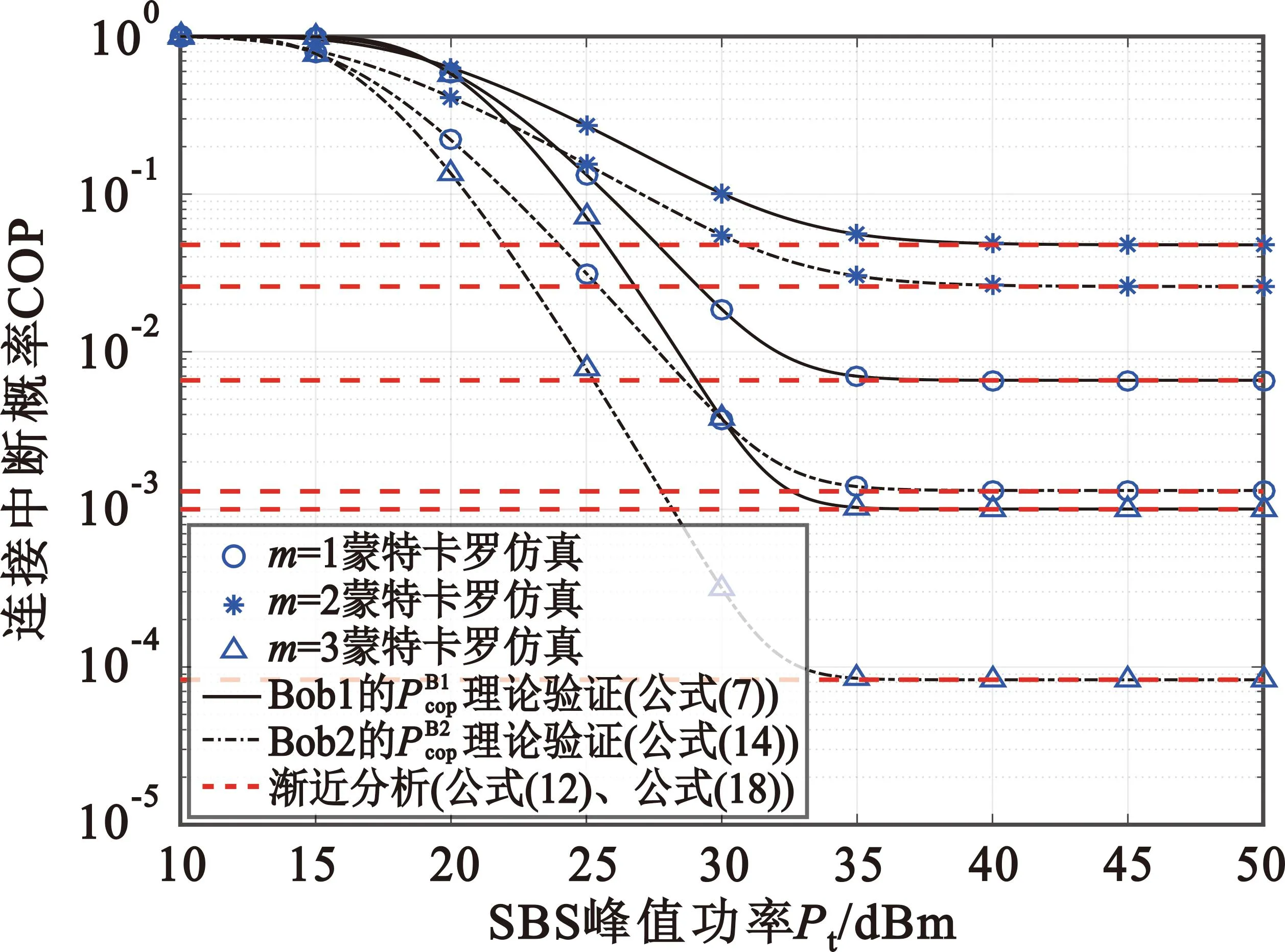
图6 次用户连接中断概率COP与信道参数m的关系Fig.6 Relationship between COP of secondary users and various channel parameters m

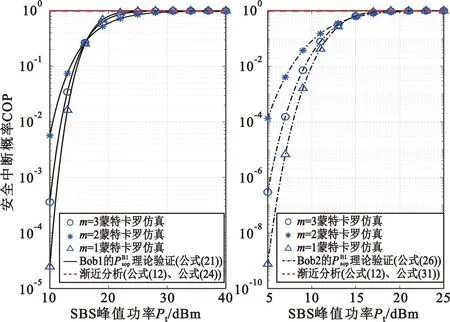
图7 次用户安全中断概率SOP与信道参数m的关系Fig.7 Relationship between SOP of secondary users and various channel parameters m

图8和图9给出瑞利信道下次用户COP、SOP与功率因子α1变化的关系,设定m=1,Pt=200 dBm。从图8中可以得到以下结论:①当α1=0.707 1,此时Bob1和Bob2的COP等于1,通信完全中断(这是因为功率因子α2过小,导致Bob1发送到Bob2信号的信息传输速率小于R2,从而产生中断);②当α1=0.546 9,此时Bob1的COP最小,且Bob2的COP也处于较小值,此时系统的连接可靠性较好。上述结论与推论2讨论部分是一致的。从图9可以观察到:①当α1>0.707 1时,Bob1和Bob2的SOP不存在(这是因为COP等于1,系统通信已经发生中断);②当ΩAE=0.4,ΩRE=0.2时,不论功率因子α1如何变化,Bob2的SOP始终逼近1,这说明SBS-Eve和Bob1-Eve的距离对次用户SOP的影响远远超过了功率因子;③为了更加直观地了解功率因子α1与次用户SOP的关系,设定ΩAE=0.04,ΩRE=0.02(以减弱SBS-Eve和Bob1-Eve距离对次用户SOP的影响),0<α1<0.561时,Bob1的SOP增大;α1=0.561时,SOP最大;0.561<α1<1时,Bob1的SOP减小(这是因为Eve需要首先通过SIC消除来自信息x2的干扰,起初Eve消除x2干扰的能力较强,随着功率因子α1不断增大,Eve窃取x1的能力变强,导致Bob1的SOP增大。α1超过0.561后,Eve通过SIC消除来自安全信息x2干扰的能力大幅下降,从而减小了Eve进一步窃取x1的机会,因而Bob1的SOP减小,安全可靠性变好);④增大功率因子α1可以增强Bob2的安全可靠性(因为功率因子α2减小,导致Eve窃取x2的能力变弱)。上述结论与定理3和定理4讨论部分是一致的。

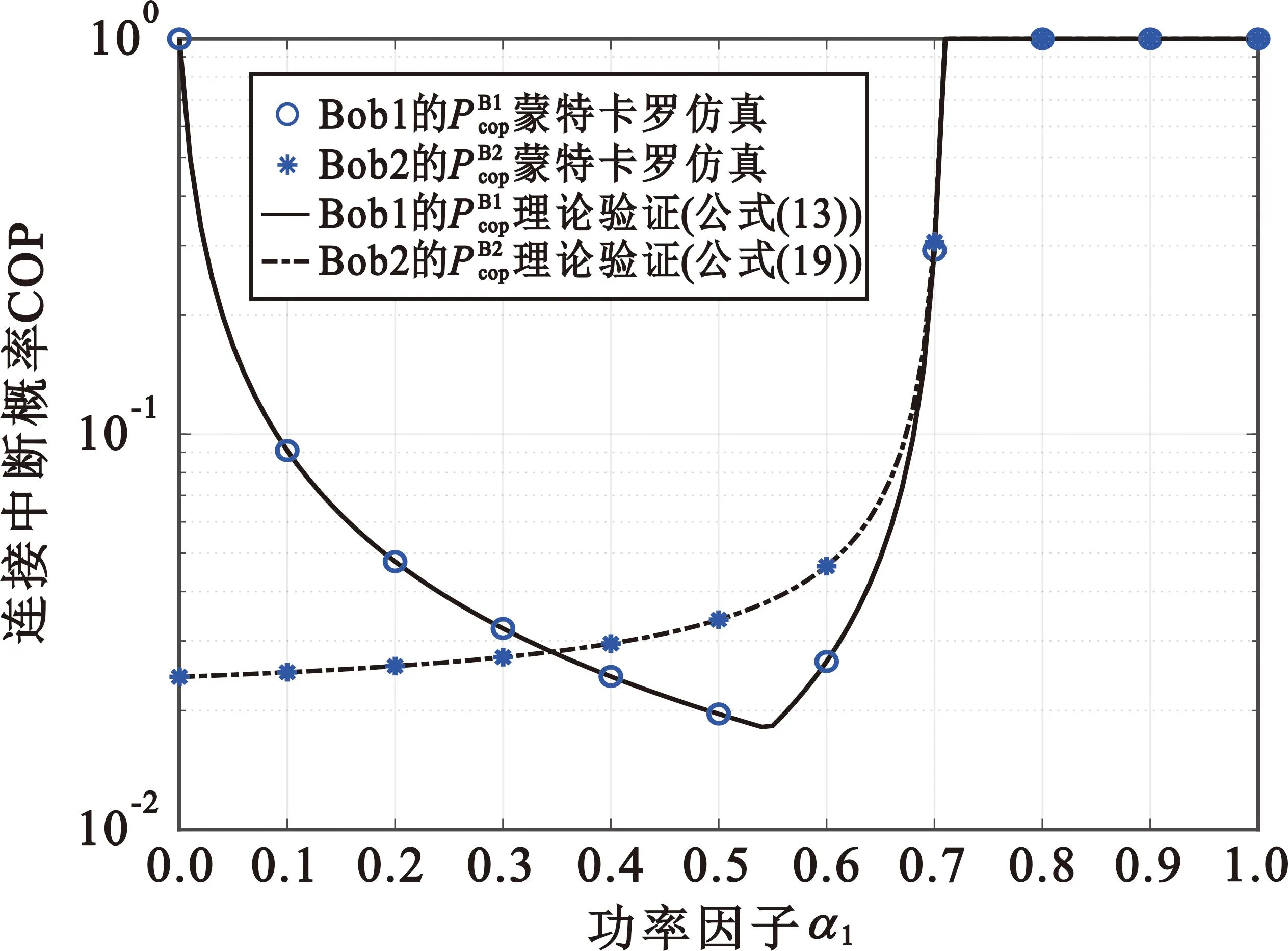
图8 次用户连接中断概率COP与功率因子α1的关系Fig.8 Relationship between COP of secondary users and various power factor α1

图10给出了瑞利信道下次用户COP与SBS-Pu和SBS-Bob1相对距离变化的关系,设定m=1,Pt=200 dBm,SBS-Bob1距离固定(ΩAR不变),SBS-Pu距离减小(ΩAP增大)。从图10可以发现,随着ΩAP增大,Bob1和Bob2的COP显著增大,系统的连接可靠性快速变差。这是因为SBS发射功率受Pu制约,Pu距离SBS越近时,为保证Pu的服务质量,SBS发射功率必须相应减小。

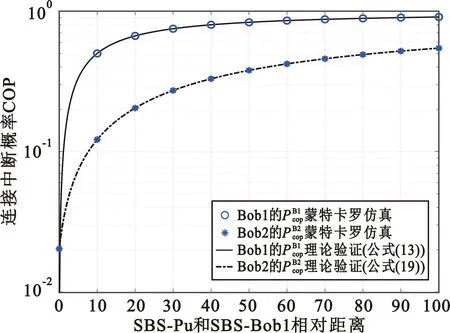
图10 次用户连接中断概率COP与SBS-Pu和SBS-Bob1相对距离的关系Fig.10 Relationship between COP of secondary users and various relative distance of SBS-Pu to SBS-Bob1

图11给出了瑞利信道下Bob1的SOP随SBS-Pu、SBS-Eve相对距离变化的关系,设定m=1,Pt=200 dBm,SBS-Pu距离固定(ΩAP不变),SBS-Eve距离增大(ΩAE减小)。此时Bob1的SOP显著减小,这是因为Eve与SBS距离变远,窃听到的信号质量变差,符合前文理论分析结果。

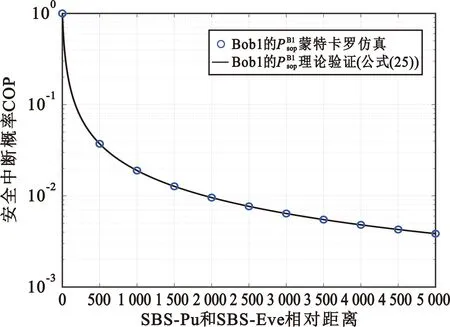
图11 次用户安全中断概率SOP与SBS-Pu和SBS-Eve相对距离的关系Fig.11 Relationship between SOP of secondary users and various relative distance of SBS-Pu to SBS-Eve

图12给出了瑞利信道下Bob2的SOP随SBS-Pu、SBS-Eve以及Pu-Bob1、Bob1-Eve相对距离变化的关系,设定m=1,Pt=200 dBm。当SBS-Pu距离固定(ΩAP不变),SBS-Eve距离增大(ΩAE减小)时,不考虑Pu-Bob1、Pu-Eve相对距离,Bob2的SOP几乎不变,说明在Pt≫Q时Bob2的安全可靠性与Pu和Eve的位置无关。当Pu-Bob1距离固定(ΩRP不变),Bob1-Eve距离增大(ΩRE减小)时,不考虑SBS-Pu、SBS-Eve相对距离,Bob2的SOP同样几乎不变。由此可以说明,Pt≫Q时,Bob2的安全可靠性与SBS-Pu、SBS-Eve以及Pu-Bob1、Bob1-Eve相对距离无关。

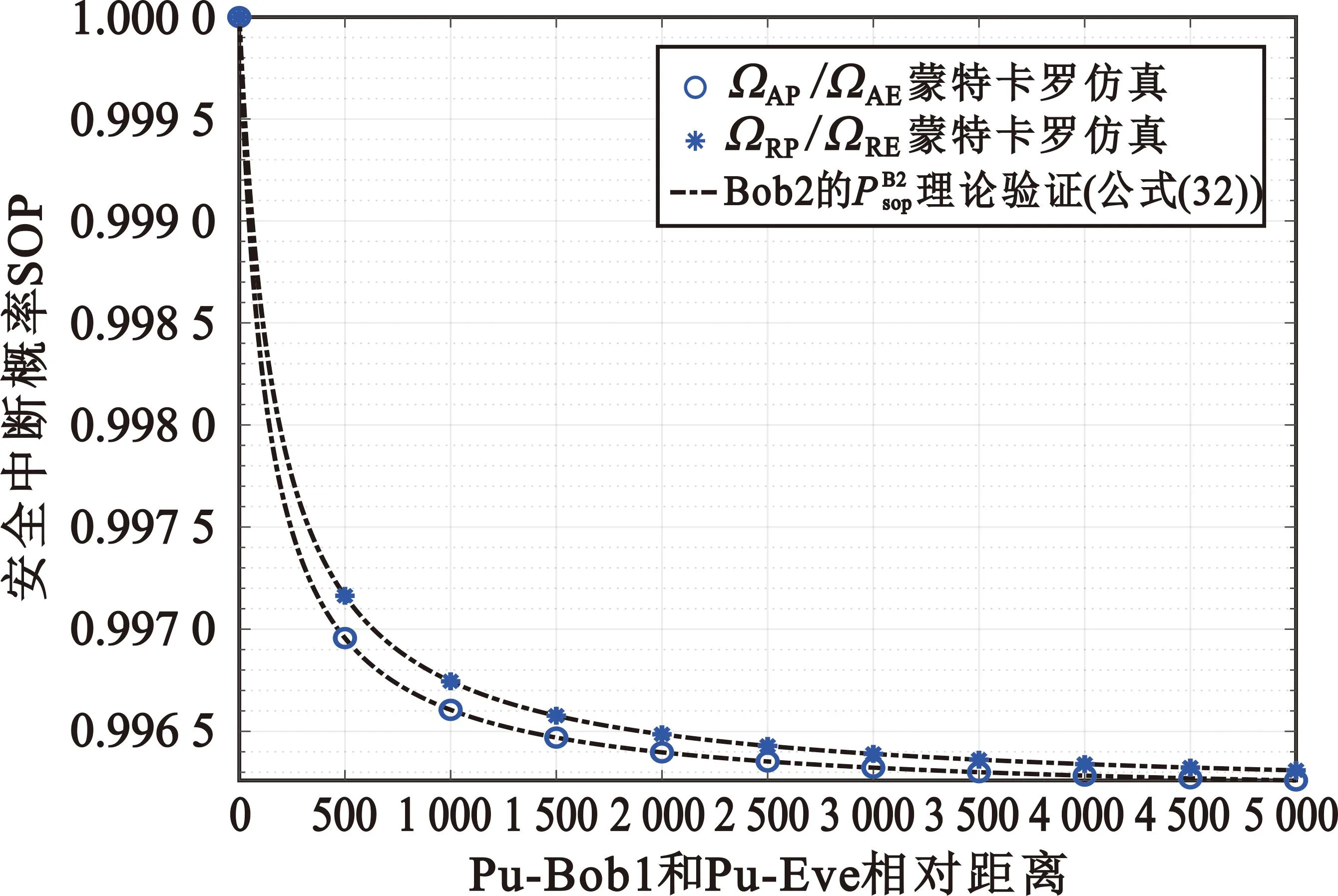
图12 次用户安全中断概率SOP与Pu-Bob1和Pu-Eve相对距离的关系Fig.12 Relationship between SOP of secondary users and various relative distance of SBS-Bob1 to SBS-Eve

4 结 论

本文研究了频谱共享CR-NOMA下行传输无线网络的物理层安全性能。为了提高频谱利用率,提出了一种中继协作网络模型。在这种CR-NOMA网络中,信道质量强的次用户作为中继,采用解码转发方式协助信道条件差的次用户传输信号。考虑了主用户服务质量约束和窃听者的实际信号处理能力,推导得到次用户COP和SOP等安全性能指标的精确闭合表达式和渐近表达式。最后,使用Monte Carlo方法仿真验证了理论分析的正确性,得到以下结论:①瑞利衰落信道下,系统的物理层安全性能优于Nakagami-m衰落信道;②干扰温度越低,系统的物理层安全性能越好;③功率分配因子α1不能超过0.707 1,超过后系统不能通信(α1=0.546 9时系统的连接可靠性最好,α1=0.561时系统的安全可靠性最差);④SBS-PU和SBS-Eve、Pu-Bob1和Pu-Eve相对距离比值变大,能够增强系统的安全可靠性;⑤当SBS峰值功率远大于干扰温度时,系统物理层安全性能不受信道增益参数影响。