基于宽深超分辨率网络的信道估计方法*
谢 朋,钱蓉蓉,任文平
(云南大学 信息学院,昆明 650500)
0 引 言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)作为通信中一种重要的抗多径技术也是5G的关键技术之一,成为了目前重要的研究对象。在OFDM传输的过程中,阴影衰落、传输路径中的损耗,以及多径影响,都有可能造成信号的畸变,影响通信系统的性能,这就要求要获得准确的信道状态信息(Channel State Information,CSI)[1],用于均衡和补偿信道的衰落。因此信道估计在此过程中显得尤为重要,信道估计的精度直接影响到了整个通信系统的性能。
信号传输过程十分复杂,干扰严重,导致信号失真[2],给信道估计过程带来了挑战。随着计算机性能的提升,神经网络在数据处理方面体现出了强大的优势,目前已有研究将神经网络算法应用在无线通信领域,如信道估计[3-10]、信号检测。文献[3]将无线信道视作黑盒,利用深度神经网络(Deep Neural Network,DNN)以端到端的方式模拟信道传输特征。文献[4]对文献[3]的工作做了进一步改进,使用DNN加长短期记忆人工神经网络(Long Short-Term Memory,LSTM)代替原本的全连接DNN网络,端到端地恢复出原始符号。这种设计使网络参数大幅缩减,收敛速度进一步加快。文献[5] 提出基于反向传播(Back Propagation,BP)神经网络的信道估计算法,通过离线的信道数据训练拟合信道特征。文献[6]提出使用集成神经网络将信道估计过程映射为含噪导频信号与原始导频信号之间的非线性关系构建,并结合差异度对其进行集成。文献[7]提出将系统的通道响应作为二维图像处理,把信道估计问题转换为二维图像处理问题。文献[8]同样将信道矩阵当作二维矩阵,通过对信道矩阵进行插值,再通过超分辨率卷积神经网络[9]重构信道矩阵,但是其网络结构简单,得出的效果并不令人满意。文献[10]针对时变信号提出了基于超分辨率生成对抗网络(Super-resolution Generative Adversarial Network,SRGAN)的信道估计方法,代替了信道估计中的插值处理。但是该方法需要的导频过多降低了频带的利用率,并且对数据的规格有一定的限制,不适用于标准OFDM信号。
针对OFDM系统中的快速衰落信道,本文提出了一种基于宽深超分辨率(Wide Deep Super-resolution,WDSR)网络[11]的信道估计算法,把传统信道估计插值方法与深度学习超分辨率方法结合,将上采样分为插值和深度学习超分辨率两步替代以往的一步插值上采样方法,将LS信道估计算法初步上采样得到的估计值作为低分辨率图像,通过离线训练的方式来训练网络调整参数,利用图像超分辨率的方法再次放大重构出高分辨率图像,即整个信道的高精度信道矩阵。算法通过LS信道估计初步上采样的预处理方法,解决了文献[10]在快衰落中对导频估计值直接通过网络放大带来的导频开销过大以及数据规格限制问题,并且WDSR网络相比之前提出的SRCNN方法对信道特征的提取能力更强,采用了残差网络能够更加准确地学习到导频与真实值之间的映射关系,更准确地重构信道。实验结果表明,所提算法相比常用的传统算法以及SRCNN算法提高了信道估计的精确度。
1 系统模型
考虑如图1所示的OFDM系统,发送端发送的数据由一系列随机生成的二进制序列组成,在传输过程中由于通信过程中的干扰和噪声导致发送端和接收端之间的信道响应失真,通常会在OFDM信号中插入导频,导频的位置以及数值完全已知。插入导频后对数据进行符号调制把数据分割到不同频率的载波上(OFDM子帧中有NS个子载波以及ND个OFDM符号),然后对数据进行快速傅里叶逆变换(Inverse Fast Fourier Transformation,IFFT)变换。由于通信中存在符号间干扰(Inter-symbol Interference,ISI)以及子载波干扰(Inter-carrier Interference,ICI),需要在OFDM符号中加入循环前缀(Cyclic Prefix,CP),得到发送端数据X。
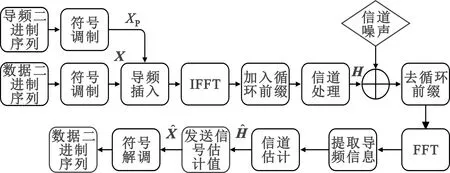
图1 OFDM系统结构Fig.1 OFDM system architecture
对于OFDM信号第k个时隙上的第i个子载波发送端信号Xi,k,其与接收端信号Yi,k之间的关系可以由式(1)表达:
Yi,k=Hi,kXi,k+Zi,k
(1)
式中:OFDM子帧的结构为(NS,ND)时间索引k的取值范围是(0,ND-1);子载波索引i的取值范围是(0,Ns-1);Xi,k代表传输信号;Yi,k代表接收信号;Zi,k代表高斯白噪声;Hi,k代表对应时隙和子载波的信道响应;H∈NS×ND是整个信道的信道响应。在得到接收信号Y后去除CP,并且进行快速傅里叶变换(Fast Fourier Transform,FFT),再利用信道估计得到的估计信道响应求得发送信号的估计值,最后通过解调可以得到相应的数据二进制序列。信道估计就是要利用已知的导频值求解使其尽量接近于真实的信道响应H。
2 基于WDSR的信道估计算法
在先前的研究中,Soltani等人[8]将SRCNN应用于信道估计问题中,然而并不是所有的超分辨率网络都适用于信道估计问题,例如增强可变形卷积网络(Enhanced Deformable Convolutional Networks,EDVR)[12]过于注重视频图像细节而无法用于信道估计。本文选用WDSR网络处理信道估计问题。
2.1 WDSR网络架构
WDSR利用残差网络的跳跃式连接,相比于SRCNN它的特征提取能力更强,并且很好地解决了梯度消失以及梯度爆炸问题。同时WDSR采用了亚像素卷积[13]的上采样方法降低了上采样的人为干扰因素,其过程如图2所示。首先通过CNN提取特征图,之后就是彩色部分所示的Pix过程。如果需要将目标图像放大r倍就需要生成r2张特征图,然后再将r2张特征图拼接成一个×r倍的放大图像,运用的是抽样的逆思想。与SRCNN相比,WDSR能够取得更好的训练效果,其结构如图3所示。
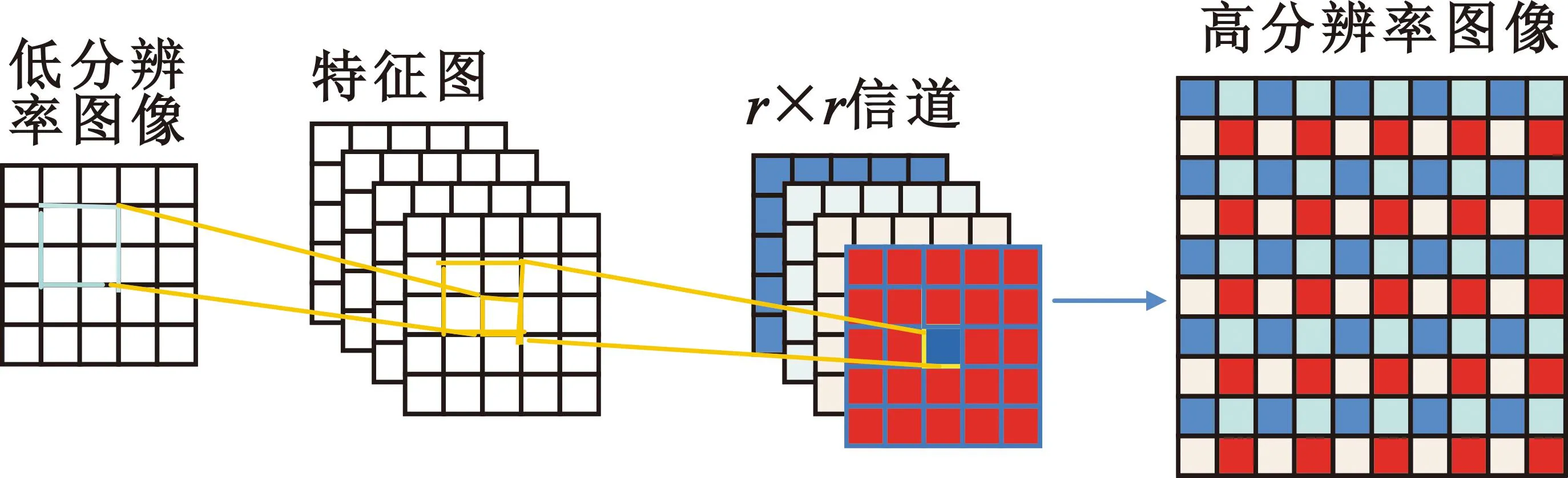
图2 亚像素卷积过程Fig.2 Sub-pixel convolution
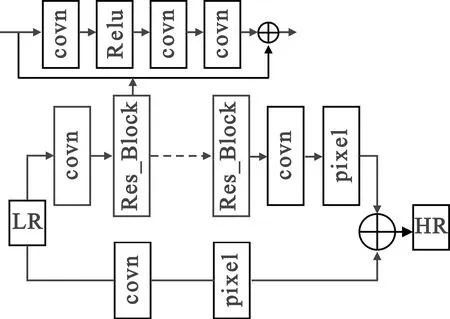
图3 WDSR网络结构Fig.3 WDSR network architecture
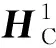
(2)
为了更好地提取低分辨率图像和高分辨率图像之间的映射关系,WDSR采用了更深的网络来进行特征提取。对于网络加深所带来的梯度消失以及梯度爆炸产生的性能下降问题,WDSR网络通过引入残差块来解决,残差块由卷积层、Relu层、卷积层、卷积层构成。其中采用的归一化方式为权重归一化(Weight Normalization,WN)[14],将权重进行如式(3)所示的标准化计算。通过实验发现,相较于批量归一化(Batch Normalization,BN),在图像超分辨率问题中WN的响应速度更快并且能取得更高的准确率,是一种更加适应于图像超分辨率问题的标准化方法。
(3)
式中:w为权值向量;v是w在欧氏范数上解耦得出的参数标量,v的物理意义为w的权值大小;g是w在欧氏范数上解耦得出的参数向量,g的物理意义为w的权值方向。根据v,g重新参数化网络中的每个权重向量w后,再对其进行随机梯度下降从而加快收敛的速度。

(4)
式中:fi代表包含归一化处理的卷积层映射关系;θi与ui对应每个卷积层的权重项和偏置项。通过残差块特征提取后,接着通过一个卷积层和WN处理,卷积核大小为3×3,通道数为r2×c。该操作为Pix提供对应数目的特征图,r为图像放大倍数,c为图像颜色通道数。然后对特征图进行Pix操作,将图像放大到目标尺寸。若输入的低分辨率图像为灰度图像(c=1),则网络上半部分输出为
(5)
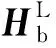
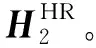
(6)
这样完成了由低分辨率图像HLR到高分辨率图像HHR之间的重构。
2.2 WDSR信道估计算法
WDSR网络的处理对象通常是是图片,因此原始WDSR网络的输入层接收的是三通道(RBG 图像)的训练数据,而在信道估计方法中需要把通过导频得到的信道响应矩阵作为低分辨率图像输入,得到整个信道的高分辨率信道响应矩阵,信道矩阵每个对应位置只有单一的值,因此要把输入层从(NS,ND,3)改变成(NS,ND,1)。信道响应的取值并没有一个固定为范围,所以要去除 WDSR网络中的归一化层。由于标准的OFDM子帧对应的时网格包含NS=72 个子载波ND=14 个时隙,因此对于标准OFDM子帧采用的是×2 WDSR 模型。训练流程如图4所示。
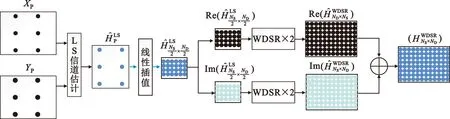
图4 WDSR信道估计算法训练流程Fig.4 Training process of WDSR channel estimation algorithm
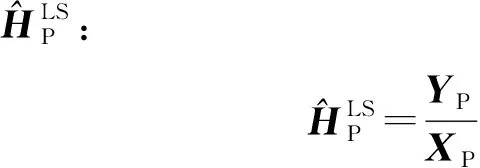
(7)
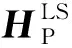
(8)
(9)
式中:Fθ(·)代表WDSR信道估计网络的映射关系;Θ为网络中的参数包含权重与偏置项。
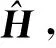
(10)
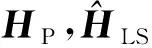
输入:导频接收端以及发送端XP,YP,不含噪声的理想信道响应Hperfect
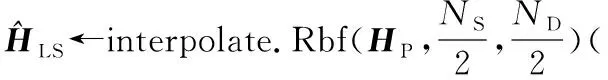
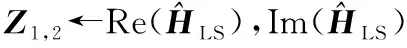
初始化:随机初始化参数Θ,t←0,mt←0,vt←0;
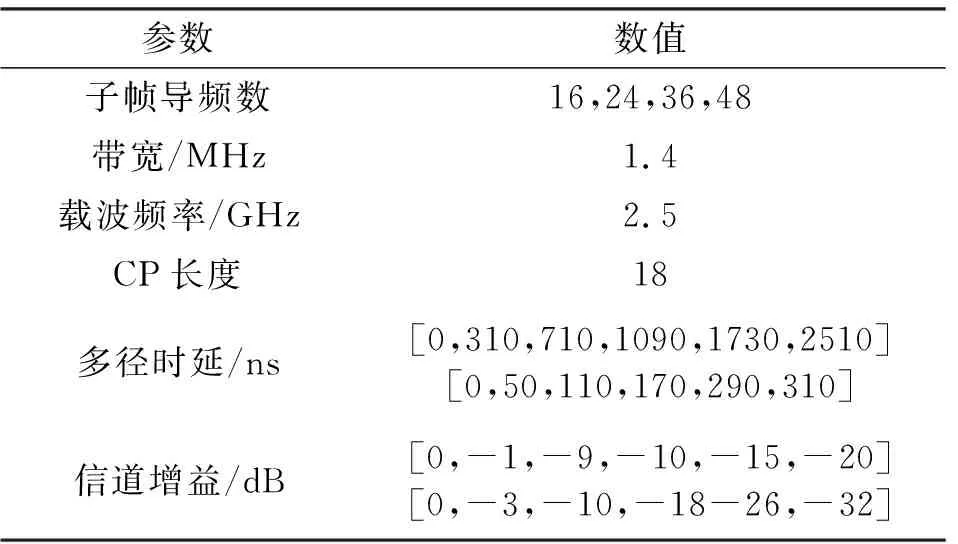
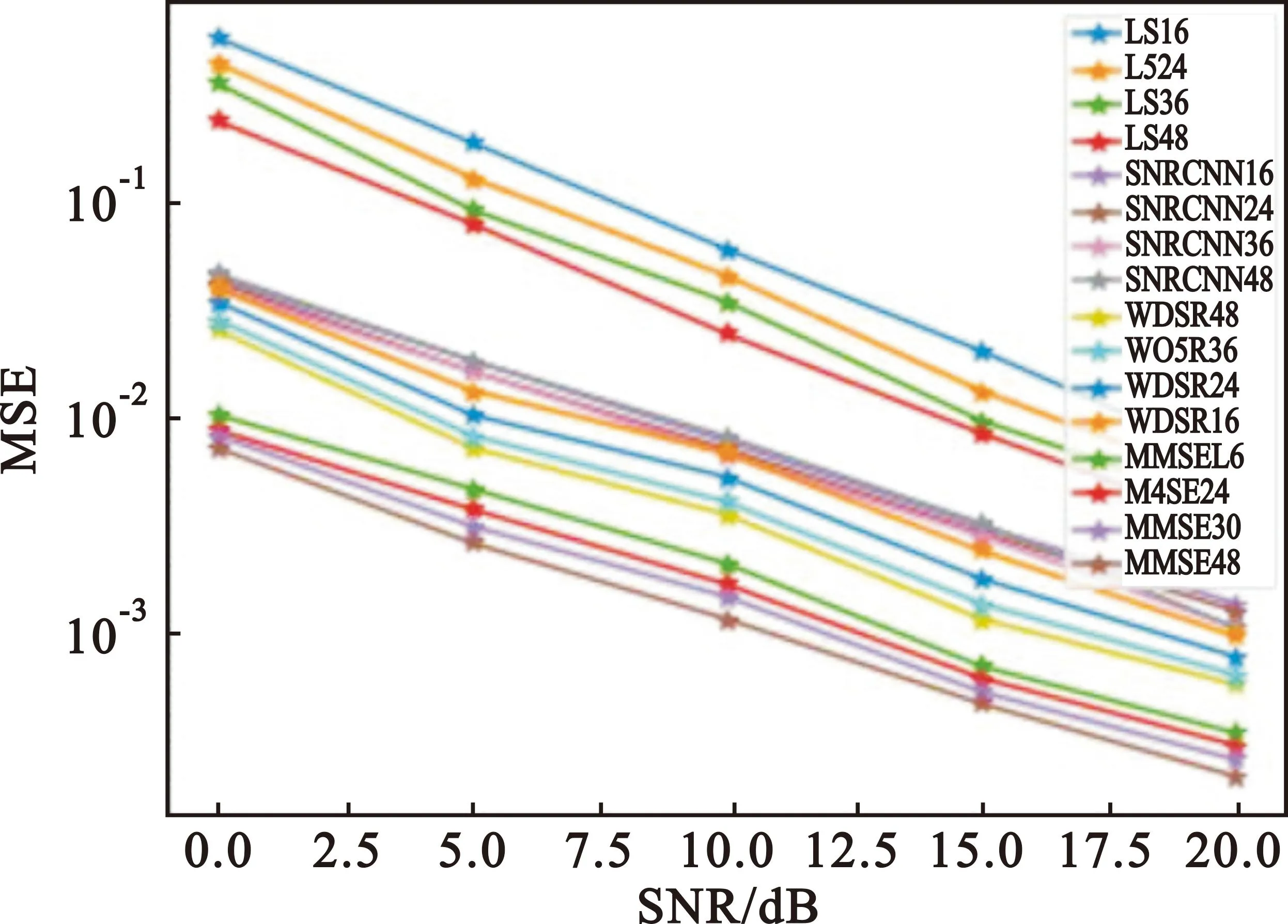
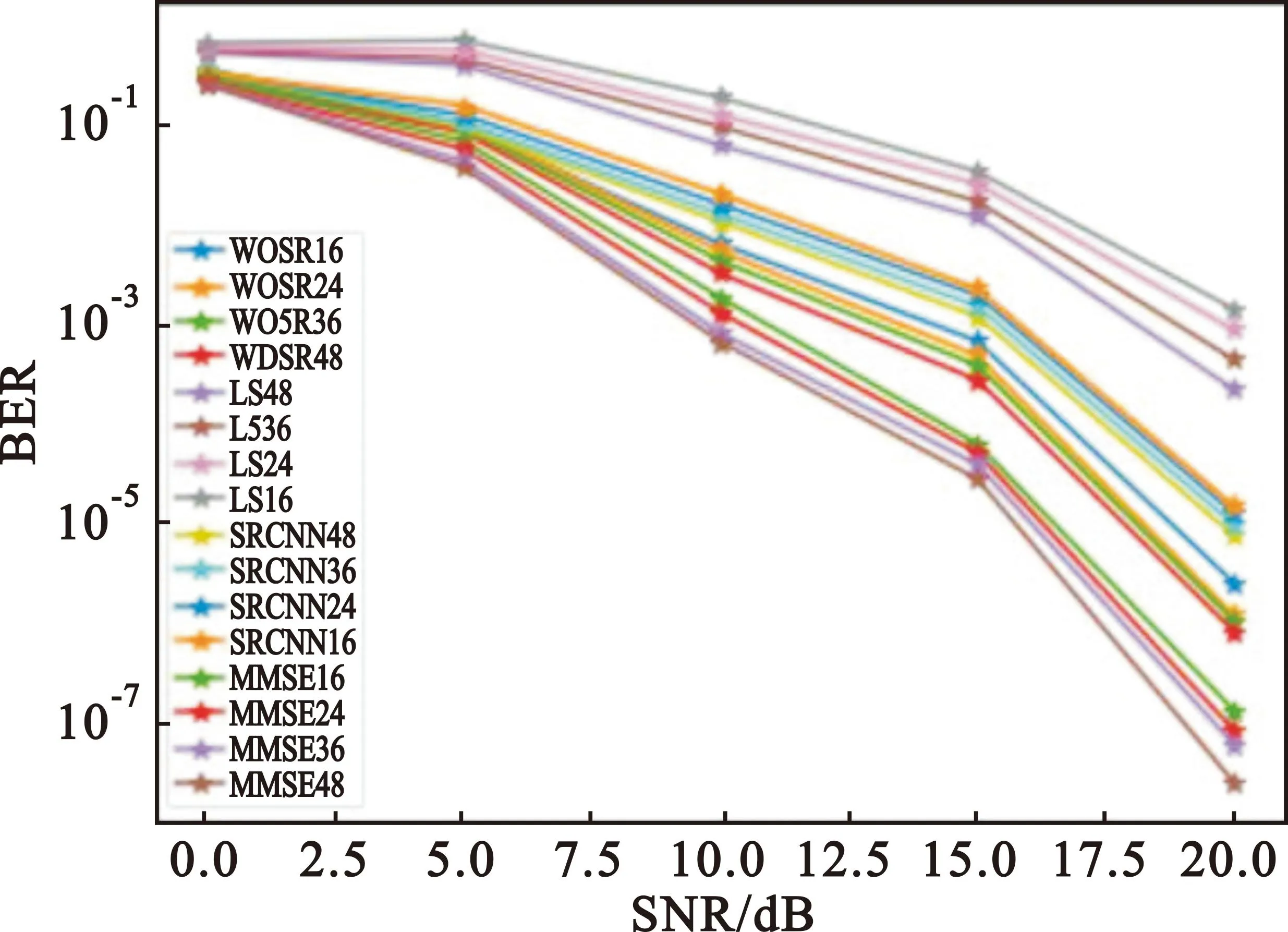
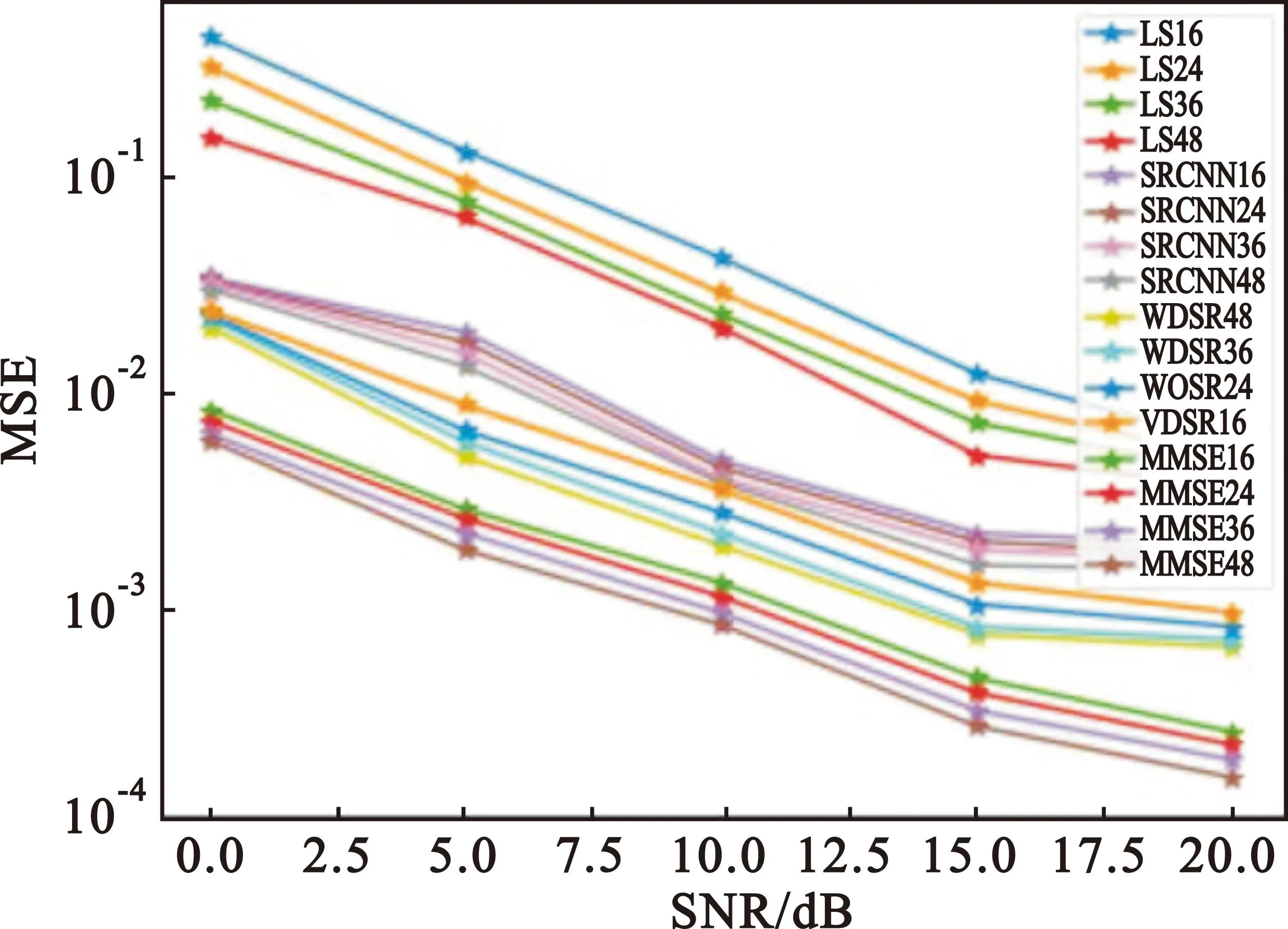
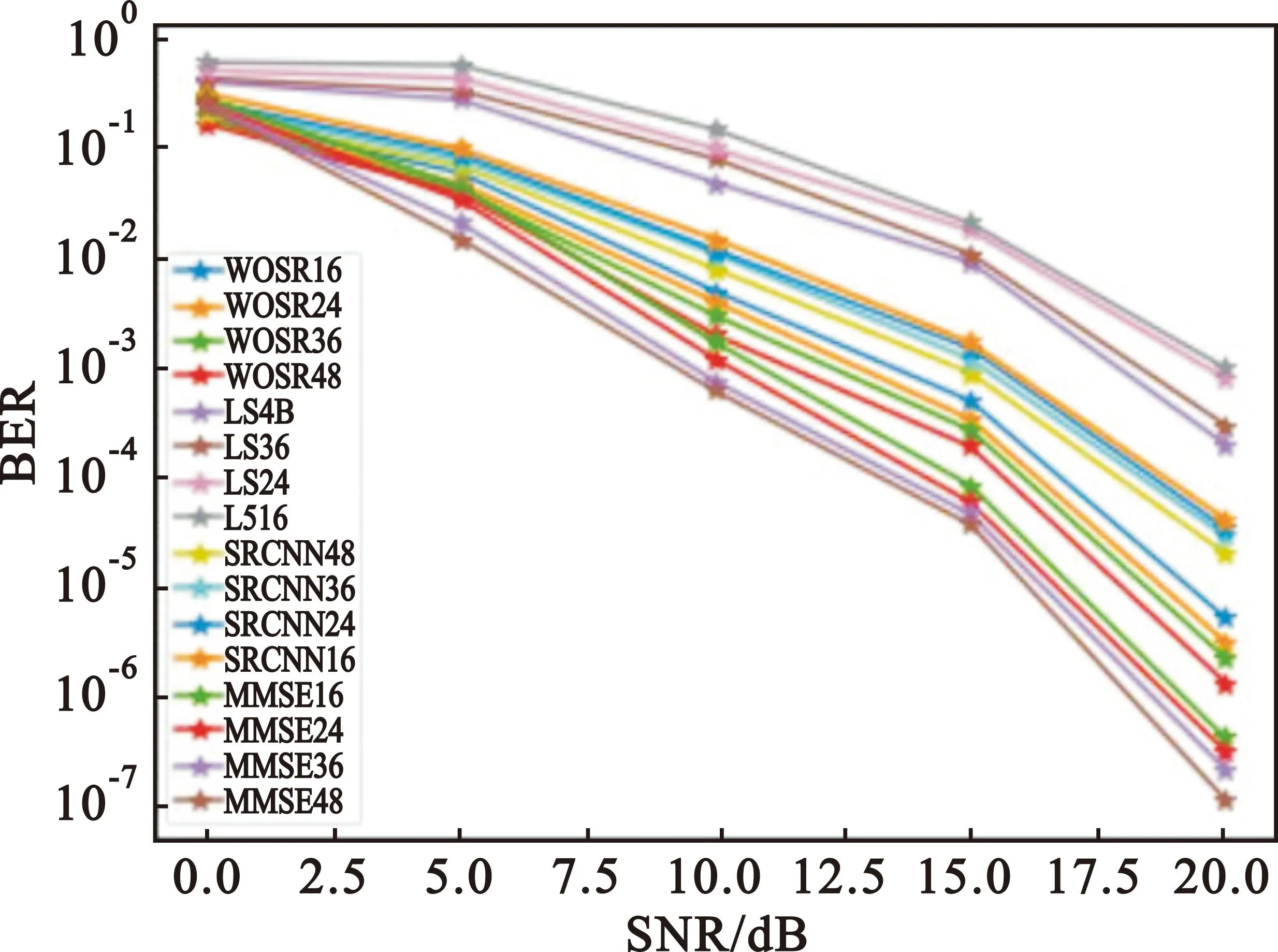
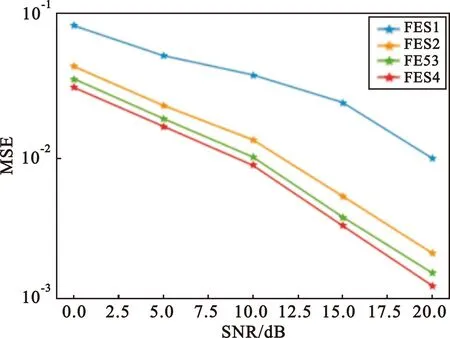
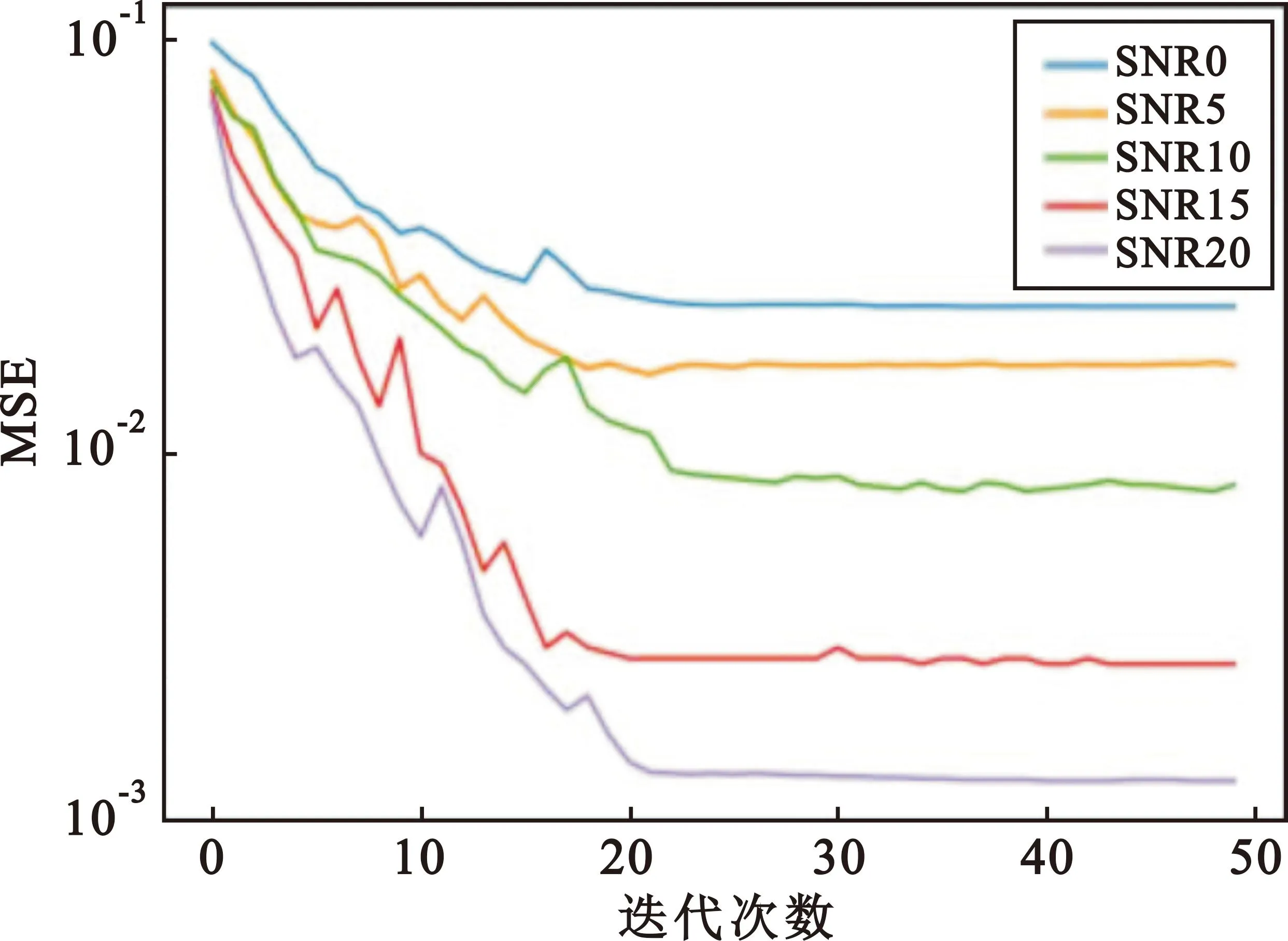
while训练次数 t←t+1(训练次数更新) mt←β1*mt-1+(1-β1)*gt(累积梯度) end while 本节通过仿真验证WDSR信道估计方法在不同场景的表现,并将结果与现行的几种算法进行对比。 在信道建模方面,使用较为常用的维也纳大学LTE模拟器[15]生成与文献[9]中同类型的车载小尺度衰落信道(Vehicular A channel,VehA)(载波频率为2.5 GHz,带宽1.4 MHz),以及行人小尺度衰落信道(Pedestrian A channel,PedA)(其多径时延和信道增益与VehA区别较大且应用场景不同:VehA作用区域较大,后者PedA作用区域较小但环境相对复杂)。将导频发送数据和接收数据通过计算得到含噪声的信道矩阵Hnoisy,之后借助LTE模拟器自带的理想信道估计功能进行单通道的理想信道估计,重复5 500次后对所得的矩阵进行拼接生成不含噪声的理想信道矩阵Hperfect。仿真中OFDM子帧由14个时隙和72个子载波组成,调制方式为BPSK,信道为快衰落信道,其他参数如表1所示。 表1 仿真参数Tab.1 Simulation parameter 仿真采用pytorch框架利用GPU加速训练来实现所提出的算法。为了使训练尽量收敛,将最大迭代次数设置为50次,训练集和测试集分别为5 000和500。训练参数如表2所示。 表2 训练参数Tab.2 Training parameter 在3.1节的仿真条件下对WDSR方法、传统信道估计方法以及SRCNN信道估计方法进行对比,图5展示了在VehA信道中不同信道估计算法的MSE和BER性能。 (a)MSE性能 (b)BER性能图5 VehA信道模型中不同SNR和导频数下不同算法的MSE和BER性能Fig.5 MSE and BER performance of different algorithms under different SNR and pilot numbers in the VehA channel model 由图5(a)可以看出,随着SNR的下降,四种信道估计方法的误差均有所下降,在假设信道先验信息已知的情况下MMSE算法具有最好的性能,但是在实际信道估计中难以实现;两种基于深度学习的信道估计算法效果均优于传统的LS信道估计方法;在给定的SNR范围内WDSR算法的效果均优于SRCNN算法。在不同导频情况下,SRCNN算法对导频数量的少量变化并不敏感;随着导频数的增加,MSE只有微量的降低,这是因为信道特征不连续而SRCNN方法采用对导频一步插值的上采样方式来进行数据预处理。WDSR算法随着导频的增多,估计的效果也随之提升;在导频数从16增加到36时MSE逐渐降低,在导频数从36增加到48时MSE的降低较为微小。WDSR网络在不同的导频数下相较于LS算法以及SRCNN信道估计算法仍然取得了较好的效果,因此可以在一定程度上节省导频的开销,提高频带的利用率。对比SRCNN算法,WDSR网络算法的MSE性能至少提高1.5 dB,最高可达到6.5 dB。 从图5(b)来看,LS信道估计方法误码率较高,因为LS算法没有考虑噪声对信道的影响所以精度较低。在信噪比较低的情况下(SNR≤5 dB),WDSR信道估计算法相较于SRCNN算法误码率性能指标提升较小;随着SNR的逐渐增大,WDSR网络算法的BER下降速度增快,在信噪比较高(SNR≥10 dB)时性能明显优于SRCNN算法。 图6对不同算法在PedA信道中的效果进行了对比。在SNR=5 dB时,对比VehA信道模型,WDSR算法相较于SRCNN算法的MSE性能提升明显。值得关注的是,在SNR=15 dB时,SRCNN算法以及WDSR算法的MSE性能出现了衰退,但是WDSR算法能够提取更多的底层信息,得到相对能接受的MSE,并且在信噪比和导频取值范围内性能指标均优于其他两种算法。 (a)MSE性能 (b)BER性能图6 PedA信道模型中不同SNR导频数下不同算法的MSE和BER性能Fig.6 MSE and BER performance of different algorithms under different SNR pilot numbers in the PedA channel model 在WDSR信道估计算法中残差块的数量影响着网络的深度和信道估计的性能。为了探究残差块对信道估计性能的影响,对不同残差块下的训练效果进行了对比,如图7所示。从图中可以看出,残差块数量RES=1时MSE指标较差,RES=2时效果有明显提升,当RES数量提升至3和4时训练效果的提升逐渐减弱。考虑到网络的深度以及训练的效果,可以根据应用需求选择RES=2或者RES=3。 图7 不同残差块下WDSR信道估计算法的MSE性能Fig.7 MSE performance of WDSR channel estimation algorithm under different residual blocks 为了研究WDSR算法的收敛性,在SNR为0~20 dB范围内进行收敛性实验,观察迭代次数以及MSE性能。为了减少残差块数量对实验的影响,残差块数量设置为3。如图8所示,MSE性能随着SNR的增大而不断提升,并且在不同的信噪比情况下网络都能在25次迭代内达到收敛。 图8 WDSR信道估计算法的收敛性Fig.8 Convergence of WDSR channel estimation algorithm 表3 计算复杂度比较Tab.3 Comparison of computational complexity 本文针对快衰落信道估计中精度不够高、导频开销过大的问题,提出了一种基于WDSR网络的信道估计方法,将导频处的估计值通过LS插值初步上采样放大后的信道矩阵拆分为实部和虚部两幅低分辨率二维图像,再利用WDSR网络再次放大重建高精度的图像,在输出端对输出的实部、虚部高分辨率图像进行重新组合得到信道估计的最终结果。将信道插值与WDSR网络结合替换了以往的信道插值,把快衰落信道估计问题转换为图像超分辨率问题,解决了信道特征不连续导致信道估计精度低、导频开销大的问题。在不同导频数和不同类型的信道中,该方法不仅信道估计的性能有所提高而且在达到相同MSE以及误码率的情况下占用的导频数更少,提高了通信的有效性。但是其缺点在于网络较深,因此未来需要对算法优化,进一步减少算法的计算量,同时需要考虑更多时变特性带来的影响。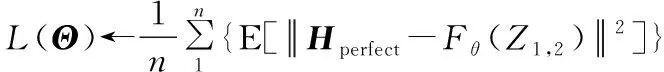

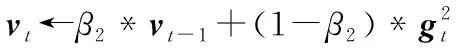
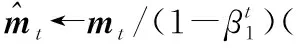
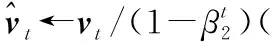
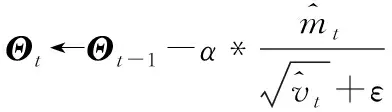
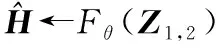
3 仿真分析
3.1 仿真参数

3.2 仿真结果
3.3 算法复杂度分析
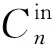

4 结束语

