动态扰动辅助的串行抵消双比特翻转Polar译码算法*

曾俏丽,陈海强,周 泉,刘远博,孙友明,黎相成

(1.广西大学 计算机与电子信息学院,南宁530004;2.广西多媒体通信与网络技术重点实验室,南宁530004)

0 引 言

Polar码是首个可在理论上被证明达到信道容量的编码技术。Arikan给出其最基础的串行抵消(Successive Cancellation,SC)译码算法,但译码性能有限。Tal等人[1]提出串行抵消列表(Successive Cancellation List,SCL)译码算法,其性能可逼近最大似然(Maximum Likelihood,ML)译码。在此基础上,Niu等人[2]将CRC码与Polar码进行级联,提出CA-SCL译码算法,获得了优于低密度奇偶校验码(Low Density Parity Check Code,LDPC)和Turbo码的译码性能[3]。这些算法获得了译码性能的提升,但增加了译码空间复杂度。Afisiadis等人[4]提出串行抵消翻转(Successive Cancellation Flip,SCF)译码算法,在译码性能提升的同时获得与SC译码相同的空间复杂度。Gerrar等人[5]将加噪译码的思想运用于SC译码上,提出串行抵消扰动(Successive Cancellation Perturbation,SCP)译码算法。Xiao等人[6]对SCP进行改进,提出了动态扰动的串行抵消(Dynamic Perturbation SC,DP-SC)译码算法。相比于原始的SC译码,SCF和SCP虽然可以获得一定的性能增益,但译码性能仍与CA-SCL存在较大的差距。

本文针对SCF受限于单比特翻转而性能提升有限问题,提出双比特翻转的SCF(Successive Cancellation Flip with 2 Bits,SCF2))译码算法;针对SCP扰动方差初始值固定的问题,通过仿真实验获取最适合的初始方差值,并对扰动噪声的方差进行改动,提出了改进算法。在此基础上,提出了一种动态扰动辅助的串行抵消双比特翻转(Dynamic Perturbation-Aided SCF2,DPA-SCF2)译码算法,并对其译码复杂度和性能进行了分析。仿真结果显示,所提出的DPA-SCF2算法在性能上获得了进一步的提升。

1 系统模型和符号定义

将二进制离散无记忆信道(Binary Input Discrete Memoryless Channel,BI-DMC)表示为W:X→Y,X∈{0,1}为输入信号,Y∈为输出信号。N个W经信道极化得到N个极化信道其中一部分极化信道的信道容量用于放置信息比特;另一部分用于存放冻结比特。

2 改进的SCP译码算法

在LDPC译码算法的研究中,随机扰动就被用于提高译码性能[7-8]。而对于Polar码,随机扰动最早被用于BP译码算法。这一策略加快了BP译码算法的收敛速度并有效提升了其译码性能[9-10]。

考虑到重复扰动会带来相同的译码结果,文献[6]提出了DP-SC译码算法。该算法采用估计序列列表P来调整σp,以便更大程度地纠正接收值的错误。文献[5-6]提出的两种算法的初始σp均固定,但经过实验仿真发现,不同Polar码的最佳初始σp值是不同的。因此,本文根据仿真结果进行初始σp值设定。考虑到调整σp是为了获得方差更大的噪声,本文提出直接对方差σp2进行改进。为了更快速简洁地获得P中最可靠的接收序列,本文对估计序列选择方案进行改进。

2.1 初始σp值的选择和σp2的步进设置

本文对码长128、码率1/2的Polar码进行测试,其中CRC设置为24。本文以σp=0.25进行左右扩展,对不同初始值下的SCP进行性能仿真。仿真结果表明,该Polar码的最优σp处在于0.3～0.35之间。为了后续调整方便,将其初始σp设置为0.3。

为了在更少的扰动次数下更快地得到正确估计序列,本文不再对噪声的方差平方根σp做修正,转而直接对噪声的方差σp2做修正,当出现相同估计序列后,使σp2=σp2+Δt,Δt为步进长度。通过仿真试验,得到(128,64)的Polar码的最优Δt为0.005。该结果将用于后续的改进SCP译码算法中。

2.2 接收估计序列选择

文献[6]提出如式(1)的可靠度判断方法:

(1)

(2)

如上所示,公式(2)仅使用ci与其对应RLL相加做一级运算,相较于公式(1)使用了乘方运算这一三级运算,降低了运算复杂度。

2.3 改进的SCP译码算法描述

根据以上描述,改进的SCP算法可总结如下:

步骤1 设置最大扰动次数为Pmax,扰动次数P_num=0,将估计列表P内部数据清零。对Y进行SC译码并作CRC校验,若能通过则输出,反之执行步骤2。

步骤6 执行σp2=σp2+Δt,且使得扰动次数P_num=P_num+1。重复步骤2直至P_num=Pmax。

2.4 改进SCP译码算法的性能分析

在这部分,本文使用校验位长度为24 b的CRC码与信息位长度为40 b的Polar码级联,得到级联CRC-Polar码,其参数为(128,64)。在AWGN信道中进行SC、CA-SCL2、SCP、DP-SC和本文所提的改进SCP译码算法的仿真,其误帧率(Frame Error Rate,FER)性能如图1所示。由图可见,随着扰动次数的增加,改进SCP译码的FER性能逐渐提升,当Pmax等于16时,改进的SCP译码算法相较于CA-SCL2译码算法 将获得约0.1 dB的FER性能增益;当Pmax达到32时,增益将提高至0.25 dB,相比于DP-SC译码算法也有约0.1 dB的FER增益。

图1 N=128,R=1/2的不同译码算法性能Fig.1 FER performance of different decoding algorithms (N=128,R=1/2)

3 双比特翻转译码算法

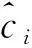
该算法的主要实现步骤如下:当初始SC译码失败后,对初始SC译码得到的估计序列进行|RLL|排序,选取其中|RLL|最小的T个比特组成翻转集合。在后续的每一次翻转译码过程中,依次在翻转集合中选择一个比特作为翻转比特,使该比特前的估计比特保持不变,对该比特进行0→1或1→0的翻转,并在此基础上继续进行SC译码。重复执行上述的翻转译码过程直至译码成功,或达到最大译码次数。但对于SC这类串行译码算法,其译码失败的原因往往不是单个比特错误造成的。为了提高SC译码的纠错能力,本文提出一种双比特翻转(SCF2)译码算法,给予SC译码2次纠错机会,在不造成译码复杂度大幅度上升的同时获得较SCF译码算法更优异的译码性能。

3.1 翻转比特位置的选择

为获取翻转比特位置集合F,需对估计序列中的K个信息位进行|RLL|排序,选取其中值最小的T个比特,将其下标放入F中。考虑到估计比特的正确性正比于|RLL|,本文提出在翻转2位估计比特时,将F[1]对应的估计比特固定为第一个翻转比特,再将F[2]～F[T]对应的T-1比特分别作为第二个翻转比特与之结合,构成双比特翻转集。为了验证F[1]对双比特翻转译码的性能影响,本文对图2所示的两种翻转比特选取方式进行了测试。

(a)翻转比特下标为F[1]+F[i]

(b)翻转比特下标为F[i]+F[i+1]图2 翻转比特下标示意图Fig.2 Flip bit index illustration

图2(a)所示方案为第一位翻转比特下标固定为F[1],第二位翻转比特下标依次为F[i],i∈2,3,…,T。图2(b)所示方案为第一位翻转比特下标依次为F[i],i∈1,2,…,T-1,第二位翻转比特下标为F[i+1]。测试结果表明,图2(a)所示翻转比特选取方案较图2(b)方案可获得更大的性能增益。

3.2 双比特翻转译码算法描述

双比特翻转译码算法流程如下:

步骤3 选取F[T_num]对应比特为翻转比特进行SC重译码并做CRC校验,校验通过则输出,否则令T_num=T_num+1,并判断是否满足T_num≤Tmax:若满足,则重新执行步骤3;若不满足,则设置T_num=2,执行步骤4。

步骤4 选取F[1]和F[T_num]对应比特为翻转比特进行重译码,并对重译码结果进行CRC校验,通过则输出,反之则令T_num=T_num+1,判断是否满足T_num≤Tmax,满足则返回执行步骤4,反之则退出译码程序。

3.3 双比特翻转译码算法的性能分析

本文使用校验位长度为24 b,参数为(128,64)的级联CRC-Polar码在AWGN信道下进行翻转译码算法的性能测试。分别使用单比特翻转译码算法(SCF)和双比特翻转译码算法(SCF2)进行译码操作,其结果如图3所示,图中译码算法名称中的(xb)表示该算法的翻转集合包含了x个翻转比特。由图可见,当翻转集合达到16时,所提算法可获得近似于CA-SCL4的译码性能,而SCF在此情况下与CA-SCL4还存在0.25～0.35 dB的性能差异。

图3 N=128,R=1/2的SCF2和SCF译码性能Fig.3 FER performance of SCF2 and SCF (N=128,R=1/2)

4 动态扰动辅助的串行抵消双比特翻转译码算法

4.1 动态扰动辅助的串行抵消双比特翻转译码算法描述

虽然两种改进算法可以带来译码性能的提升,但是改进的SCP译码算法无法针对某个指定比特进行纠正;当译码错误多于2 b时,SCF2则无法纠正。基于此,本文提出一种动态扰动辅助的串行抵消2比特翻转(DPA-SCF2)译码算法,在进行随机扰动后仍无法正确译码时,转而对其执行SCF2译码。算法描述如下:

4.2 动态扰动辅助的串行抵消双比特翻转译码算法性能分析

仿真采用2PSK调制的(128,64),(128,96)以及(256,128)3组Polar码,其CRC校验比特都为24 b。仿真对比的算法包括DPA-SCF2译码算法、SC译码算法、CA-SCL译码算法以及SCF、SCP的改进译码算法,仿真结果如图4～6所示。图中扰动译码算法名称后的(x)表示算法执行x次扰动运算,图5和图6的T_max=16。

(a)翻转算法最大翻转次数T_max=8

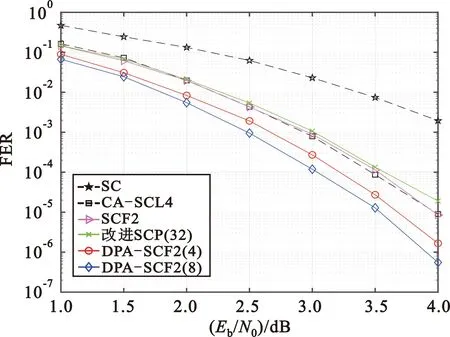
(b)翻转算法最大翻转次数T_max=16图4 (128,64) Polar码FER性能Fig.4 FER performance of Polar code (128,64)

图5 (128,96) Polar码FER性能Fig.5 FER performance of Polar code (128,96)

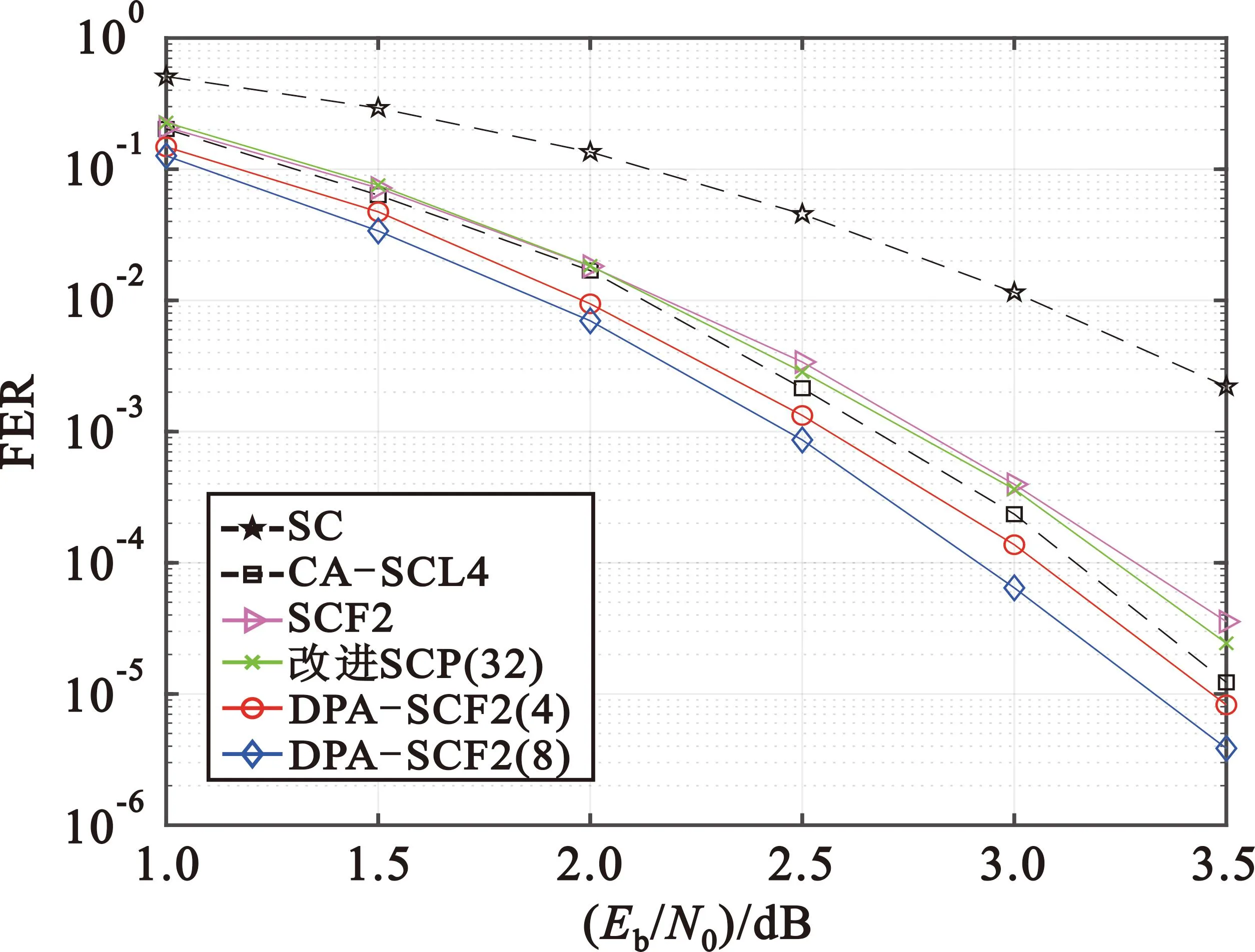
图6 (256,128) Polar码FER性能Fig.6 FER performance of Polar code (256,128)

由图4可以看出,随着T_max的增加,原本FER性能落后于改进SCP的SCF2译码算法将超越改进SCP而接近CA-SCL4。受SCF2在T_max增加时所带来的影响,DPA-SCF2在T_max=16时获得比T_max=8高出约0.35 dB的FER增益。当最大扰动次数P_max达到8时,DPA-SCF2较CA-SCL4可获得约0.5 dB的FER性能提升。从图5可以看出,当T_max=16,P_max=8时,DPA-SCF2较CA-SCL4可获得约0.45 dB的FER性能提升。从图6可以看出,DPA-SCF2较CA-SCL4最多可以获得约0.25 dB的性能增益。

5 复杂度分析

首先,对SCF2译码算法和改进的SCP译码算法的复杂度进行分析。对SCF2而言,其复杂度可计算为Tmax次单比特翻转译码的复杂度O(Tmax·NlbN)和(Tmax-1)次双比特翻转译码的复杂度O((Tmax-1)·NlbN)之和,即O((2Tmax-1)·NlbN),而Tmax为最大翻转次数,因此O((2Tmax-1)·NlbN)也是一次SCF2译码所产生的最大译码复杂度。对改进的SCP译码算法而言,其复杂度相当于Pmax次SC译码,即O(Pmax·NlbN)。在此基础上,可以轻松地获得动态扰动辅助的串行抵消双比特翻转译码算法的译码复杂度。

对DPA-SCF2而言,其第2步执行的SC译码,译码复杂度为O(NlbN)。而第3步和第4步均在当前帧的SC译码失败后才会被执行,假设每帧SC译码失败的概率为Pe,则第3步的平均译码复杂度可计算为O(Pe·(2Tmax-1)·NlbN),第4步的可计算为O(Pe·Pmax·NlbN)。由前面的算法描述可以看到,当改进SCP译码失败后,SCF2会被继续执行。因此,第3、4步的译码复杂度可共同计算为O(Pe·(Pmax+1)·(2Tmax-1)·NlbN) 。因此,总体上DPA-SCF2的平均译码复杂度为O(Pe·(Pmax+1)·(2Tmax-1)·NlbN+NlbN)。需要指出的是,式中的Pe反比于信道中的信噪比[11]。因此,当系统的信噪比增大到一定程度时,DPA-SCF2的译码复杂度接近SC译码的O(NlbN)。

为更直观地显示所提算法的复杂度,本文对SC译码算法、CA-SCL4译码算法、翻转比特集合为8的SCF2译码算法、加噪次数为32的改进SCP译码算法,以及翻转集合为8、加噪次数分别为4和8的DPA-SCF2译码算法这6组算法进行平均 SC 译码次数仿真,结果如图7所示。

图7 各算法平均SC译码次数对比Fig.7 Average SC decoding number for each algorithm

由图7可见,当信噪比达到2.0 dB时,所提出的改进SCP译码算法、双比特翻转译码算法,以及动态扰动辅助的串行抵消双比特翻转译码算法均获得了低于CA-SCL4的平均SC译码次数;当信噪比增加时,上述算法的平均SC译码次数均趋向于1,可获得接近SC译码算法的译码复杂度。

6 结 论

本文在SCP和SCF两种Polar码后处理译码算法的基础上,提出了改进的SCP译码算法和双比特翻转译码算法(SCF2)。仿真实验显示,两种改进的算法都能获得一定的性能增益。结合本文提出的双比特翻转和可变方差扰动机制,进一步提出了一种动态扰动辅助的串行抵消双比特翻转(DPA-SCF2)译码算法。在复杂度方面,所提算法在大信噪比区域,其译码复杂度接近SC译码;在性能方面,相比于列表长度为4的循环冗余校验辅助串行抵消列表(CA-SCL)译码算法,最大可获得约0.5 dB的增益。需要指出的是,所提出的译码算法适用于不同的码长和码率,其译码性能随着最大翻转次数和最大扰动次数的增加而有不同程度的提升。