基于自适应密度邻域关系的多标签在线流特征选择

张海翔,李培培,胡学钢

(1.蚌埠医学院附属合肥市第二人民医院 讯息处,安徽 合肥 230012;2.合肥工业大学 大数据知识工程教育部重点实验室,安徽 合肥 230601)

0 引 言

多标签分类处理特征数据对应多个标签问题[1-4]。例如老年人群体就医时可能患有多种常见基础病:高血压、糖尿病、血脂异常等。药物治疗时遗漏病因或过敏史都将产生严重医疗事故。同时多标签数据通常伴有高维度、冗余特性,在分类过程耗费更多时间和空间,分类精准度也会受到影响[5]。因而,在多标签学习预处理阶段需要采取特征降维操作。

特征降维方法分为两种:特征提取和特征选择。特征提取方法[6]将原空间映射或变换低维空间,该过程会破坏数据特征的原有结构,不利于后续操作。特征选择方法[7-8]从原空间提取具有代表意义的特征子集,保留原特征空间结构,分类时可直观体现性能与特征的关系,常见方法如:过滤器、包装器和嵌入技术。过滤技术[9-11]独立于算法根据训练数据的一般特性(如互信息、粗糙集理论)选择合适特征,基于一组标准对特征进行评分删除评分较低的特征。包装器技术[12]利用一个特定的算法作为特征选择过程的组成部分其结果更有效,但该方法耗时较长。嵌入式技术[13]将特征选择过程集成到学习模型的构建中,需要迭代矩阵反演计算。以上方法考虑数据事先全部获取,现实数据并非一次性全部到来。例如,随时间推移和用药影响患者病情和生命体征在不断变化,传统离线批处理特征降维方法无法满足病情诊断精准判断[14]。

流特征选择方法随着时间推移,特征一个接一个地流入,必须在每个时间戳中决定保留还是丢弃新到达的特征,并且在学习之前不知道整个特征空间的信息,最终从已到来数据中选出代表特征子集。例如,利用模糊互信息作为相关性和冗余度评价指标的OSFS(在线流特征选择)[15]方法,该方法包括两个步骤:在线相关性分析决定最新到来的特征是否保留或丢弃;在线冗余分析去除已选特征子集中的冗余特征。根据这两步分析原理,OM-NRS[16]用邻域粗糙集代替模糊互信息作为评价指标。I-SFS[17]基于互信息的相关性和冗余度,利用多目标布谷鸟搜索技术优化两个目标,但以上多标签流特征方法需要预先设定参数值,不同数据集上如何确定统一参数阈值存在一定困难。基于改进邻域粗糙集的多标签流特征选择方法(ML-OFS-ANRS[18])采用新的GAP邻域关系,在学习前不需要域信息,也不需要预先指定任何参数,采用最大依赖和最大重要性标准进行特征冗余分析,且该方法的重要性最优阈值参数对不同数据集需要设置不同值。

基于此,该文提出自适应密度邻域关系的多标签在线流特征选择方法(ML-OFS-ADNR),在依赖关系计算时根据周围实例的密度信息自动确定邻域个数,不需要预先指定任何参数。同时采用模糊等价约束方法可以挑选出高依赖度低冗余度的特征,使得所选特征子集规模较小且具有判别性。迭代执行以上步骤,直到数据全部到来。该文主要贡献如下:(1)基于邻域粗糙集理论,提出自适应密度邻域关系的多标签在线流特征选择方法(ML-OFS-ADNR),该方法在特征依赖计算时无需领域知识;(2)根据周围实例的密度信息提出新的邻域关系,利用该关系可以在在线特征选择过程中自动选择适当数量的邻域,不需要预先指定任何参数;(3)ML-OFS-ADNR采用模糊等价约束进行冗余分析,使所选特征子集具有较低的冗余度。基于粗糙集的特征选择方法通常采用特征显著性等于零的条件进行特征冗余分析。然而,在真实的数据集中,完全相等的约束过于严格。在模糊等价约束下,可以考虑更多的候选特征进行特征冗余分析,使得最终选择的特征子集小且具有鉴别性。10个基准数据集实验结果显示,ML-OFS-ADNR在相同数量的特征下,比传统特征选择方法和现有在线流特征选择方法具有更好的性能。

1 相关工作

1.1 批处理特征选择方法

特征选择在处理高维数据上可以实现更快的模型训练,降低过拟合的敏感性,抵消维数灾难带来的影响,减少数据分析期间的存储、内存资源消耗。近十年来,研究人员提出许多离线环境下的降维方法,可分为特征提取[19-20]和特征选择[21]。前者是通过对原始特征进行线性或非线性组合来构造一些辅助特征,后者是从给定原始特征中选择最具区分能力的子集。根据标签分类应用场景又可分为单标签特征选择和多标签特征选择[22]。然而上述大多数方法考虑离线环境下,数据全部已知的批处理模式,在流特征环境中这些批处理方法无法直接应用,该环境下数据集无法一次性全部获取,无法提前获取全部数据信息。为增强学习模型的可解释性,便于在现实环境中广泛应用,研究人员更加重视特征选择方法,进一步从静态数据扩展到流数据环境[15]。

1.2 多标签流特征选择方法

流数据环境下特征会随着时间的推移到来(理论上无限制),在按顺序提取新特征的过程中还要剔除已到来特征数据的冗余,确保每一轮获得最优特征子集。已有多标签流特征选择方法包括OMGFS[23]和ML-OFS-ANRS[18],SFSCI[24],PSO[10],G-SFS[17]。OMGFS基于邻域对称不确定性和邻域互信息,考虑在线特征固有群结构,根据不同数据集类型设置相关性参数阈值。ML-OFS-ANRS提出新的GAP邻域在线流特征方法,采用最大依赖最大重要性进行特征冗余分析,对数据集环境要求较高,且重要性阈值最优参数根据不同数据集需要设置不同值。针对类不平衡数据环境,SFSCI根据特征和标签之间依赖关系进行特征选择,模型学习前需提前确定最近邻参数值。PSO提出一种三相滤波过程,在多目标优化设置中将进化粒子群优化技术应用新到来特征组,检查当前组中选择特征对已选择特征的冗余性,丢弃已选择特征列表中相对新到来特征而言不重要的特征。G-SFS将多目标布谷鸟搜索技术交替应用新到来特征组,从I-SFS构建相应的G-SFS。

传统的特征降维方法需要事先获取数据集的内容,在流特征环境下由于特征并非一次性全部到来,因而传统方法无法直接应用。已有的流特征方法大多需要预设相关参数,在实际应用中不同数据集的来源和空间结构不同,无法做到为每一个数据集预设最优统一参数值,且改进邻域粗糙集方法在特征冗余筛选过程中对真实数据集过于严格导致所选特征子集中存在冗余特征,在参数设置上也无法做到完全自适应。针对现有问题,基于模糊粗糙集理论,所提出的方法在学习之前不需要指定任何参数,并被证明在处理现实世界的数据集时是有效的。

2 在线流特征选择多标签分类方法

定义流特征选择OSFS=(U,C∪D,t),其中U为非空有限数据集,C为条件属性集,D为决策属性集。C=[x1,x2,…,xn]T∈Rn×d,由d维特征空间上F=[f1,f2,…,fd]T∈Rd的n个样本组成。D=[y1,y2,…,yn]T∈Rn×l,由决策特征空间上L={l1,l2,…,lm}的n个样本组成。时间戳t时,到来新特征f,学习映射函数h:xi→L(xi∈C),得到具有代表意义的最佳特征子集。

2.1 基于自适应密度邻域的多标签特征依赖

邻域关系现有技术分为两种:距离固定(δ邻域)或邻域数固定(k最近邻域)。不同数据集数据分布不同,无法做到预设统一的参数。借鉴数据实例分布关系确定参数值作为一种新特征依赖方法受到关注。文中邻域关系确定由实例周围的密度信息自动确定邻域个数。

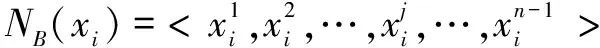
(1)

(2)

其中,k为xi密度邻居个数,表示在标签yl下标签和相同时值为1,不同为0。第四步,根据求出ft在标签yl下的特征依赖值总和最后重复三、四步得到每一个标签下ft的依赖值

2.2 自适应密度邻域粗糙集的在线特征选择

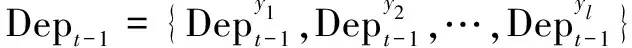
(3)

实现新到来特征筛选后,如果直接将其加入已筛选特征子集Ft,容易产生较多冗余特征,导致模型性能降低,因而新特征筛选后还需对特征子集进行冗余优化。对新到来数据ft,根据依赖计算度计算方法得到依赖值Dept。其次比较Ave_Dept-1与Dept,如果Dept中均小于Ave_Dept-1,则认为ft较已选特征子集Ft-1依赖性较低,丢弃。若满足,再比较已选特征集Ft-1与合并特征集Ft-1∪ft的依赖关系,当Ave_DepFt-1∪ft大于Ave_Dept-1,意味着添加新特征ft会增加已选特征集Ft-1的依赖性,那么将ft加入Ft-1中,否则判断Ave_Dept-1与Ave_DepFt-1∪ft之差对Ave_Dept-1的比值分析特征冗余性。对特征集Ft-1∪ft中的每一特征从候选特征集合中随机选择一个特征f,计算f显著性值(即Ave_DepFt-1∪ft与Ave_Dep(Ft-1∪ft)-f的差值),将显著性等于0的特征丢弃。通过这种新的在线流特征选择算法,可以选择高相关性、高依赖性和低冗余度的特征。

3 实验及其结果分析

3.1 实验数据集与评价指标

本节给出在实验数据集上所提方法的实验结果优势,其中选取的数据集均为常见多标签分类方法实验数据集,数据来源于Mulan(http://mulan.sourceforge.net/datasets.html)和Meka(https://waikato.github.io/meka/datasets/),详细信息见网站内容介绍。表1给出了10个实验数据集介绍,包括:样本数、特征数、标签数、数据领域。数据领域包括网页文本、电子邮件、音乐及基因功能,例如电子邮件Enron数据集共有1 702个数据,每条数据至少从属53种标签的一种或多种。

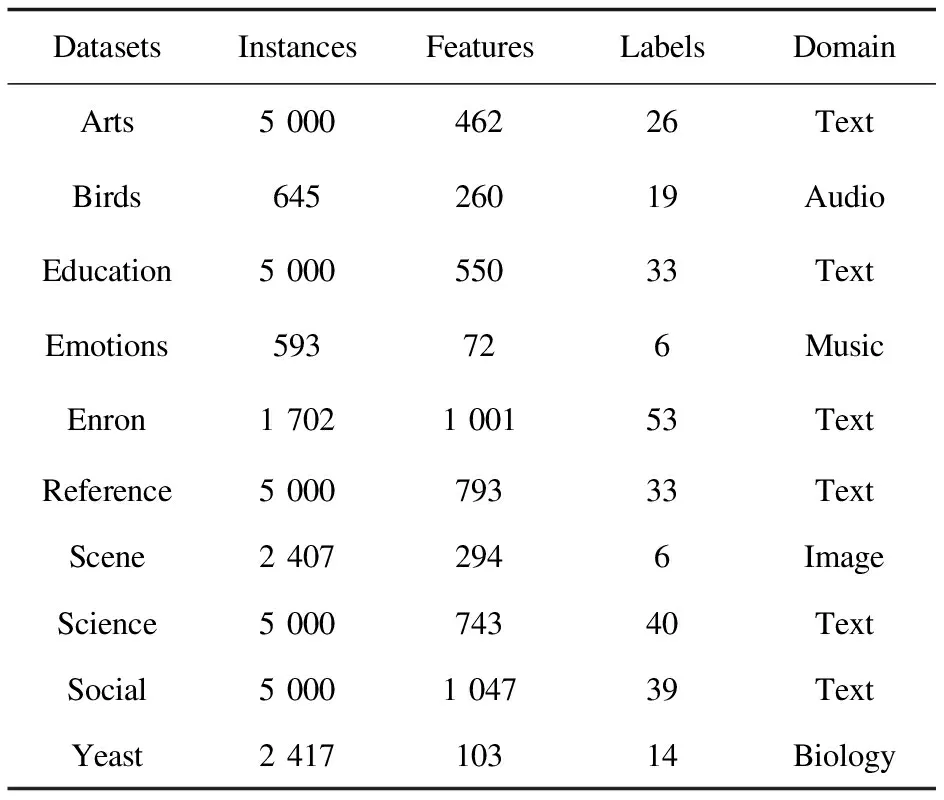
表1 数据集

将所提方法与5个批处理方法和2个流特征选择方法进行对比。其中MDDMspc[6]通过判别特征与标签间依赖最大化实现降维。GLOCAL[26]通过学习潜在标签和标签流形化实现降维并考虑标签的全局、局部相关性。LLSF[27]学习各标签的特定数据实现多标签特征选择。LSML[28]解决在缺失标签环境下的多标签特征选择问题。MCLS[29]通过将原始逻辑标签转化数字标签实现实例相似度约束。SFSCI[24]处理在类标签不平衡环境下流特征选择。ML-OFS-ANRS[18]提出自适应邻域粗糙集流特征选择方法,利用最大依赖、最大重要指标筛选特征子集。所提方法模糊等价约束参数按照相关参数设置0.05[25],其余无需任何参数,使用MLKNN分类模型评估算法性能。

3.2 实验结果分析

3.2.1 所提方法与批处理方法对比

(4)

其中,Ri(yj)是样本xi的标签yj预测等级。

Ranking Loss描述样本标签对被反向排序的平均比例:

RL=

(5)

Coverage计算平均所需的步骤数,以向下推进标签列表并覆盖所有实例的适当标签:

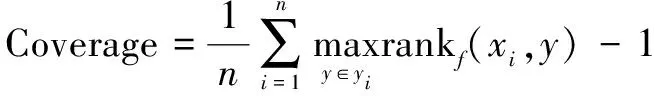
(6)

One-error计算一个不相关的标签被排在首位的次数:

(7)

Hamming Loss计算错误分类标签的平均得分:

(8)

Δ表示两组间对称差。

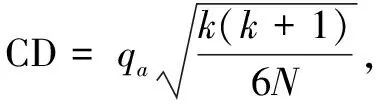
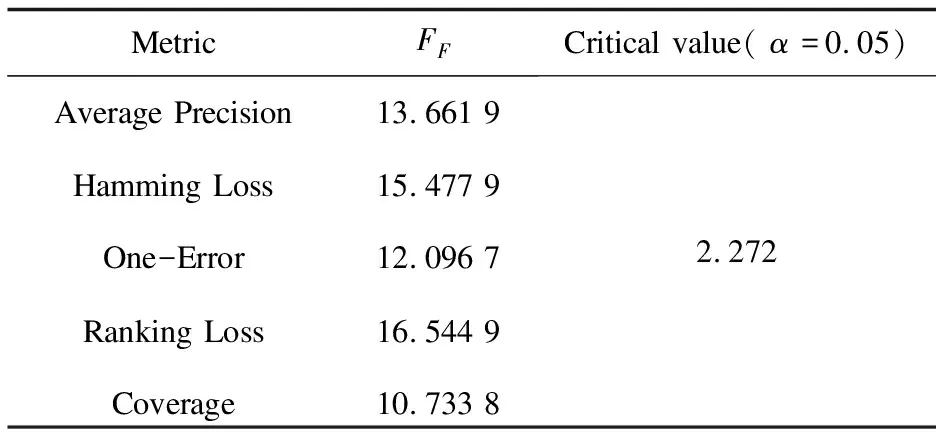
表2 在0.05显著性水平条件下FF每种评估方法的临界值

在5个评价指标上均显著优于MDDMspc和CLS,原因在于MDDM在标签处理上忽略了标签之间潜在的关联关系,所提方法引入密度邻域关系且利用平均依赖度最大限度考虑标签之间的内在联系,而MCLS在特征选择过程未对特征冗余进行过滤,取得的特征子集非最优,而ML-OFS-ADNR不仅对单个特征进行依赖度分析,而且分析新特征加入后是否对原有特征产生冗余。在线筛选过滤得到最优特征子集。

与LLSF,GLOCAL和LSML的对比中,虽然没有在所有指标上取得全部优势,但是无论在具体数据集还是CD图上综合排名所提方法最好。由于在密度邻域依赖度计算过程中仅考虑在密度信息范围内忽略密度范围以外的标签信息,无法最大化利用标签空间相关性信息,所提方法的CD非显著最优。

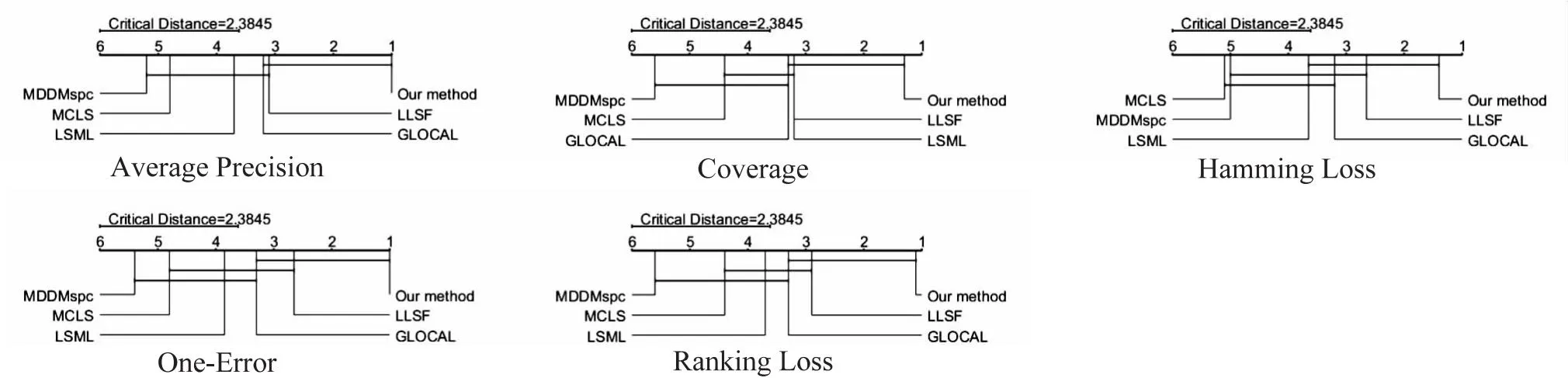
图1 所提方法与对比算法的Nemenyi检验比较结果

3.2.2 所提方法与流特征选择方法对比

除与批处理方法对比外,还在多标签特征流环境下与最新的SFSCI[24],ML-OFS-ANRS[18]在指标Average Precision和Ranking Loss上进行比较,实验结果见表3。

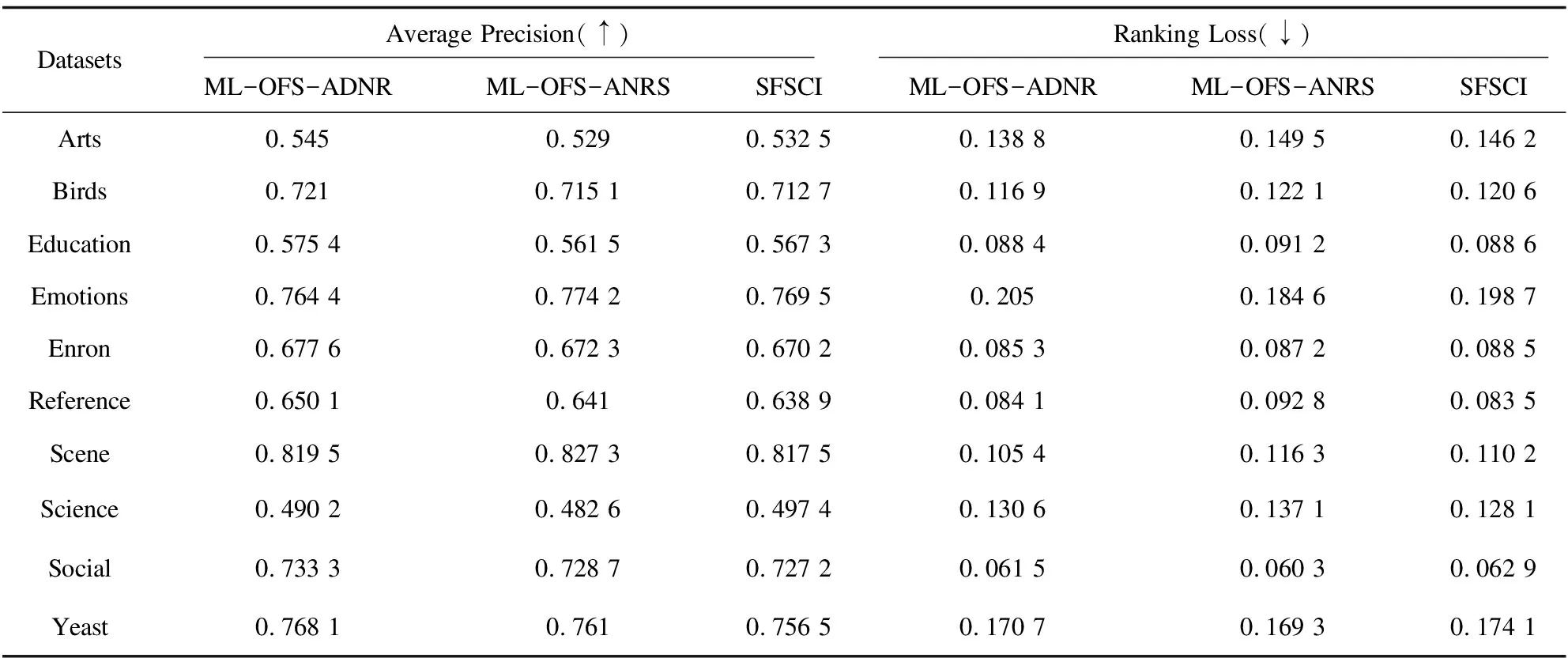
表3 ML-OFS-ADNR与SFSCI,ML-OFS-ANRS对比结果

根据表3可知:(1)基于密度邻域粗糙集无需预设参数,根据密度信息自动确定邻域个数而SFSCI在实验前需要手动设置最大邻居数K,表明所提方法在Average Precision明显优于SFSCI,Ranking Loss上也有超过一半数据结果优势。(2)在其他数据集上,所提方法均优于SCSFI,原因在于密度邻域关系可以根据数据集的不同类型自动选择合适的邻域个数,而SCSFI的K值设定忽略数据集内容,限制模型的可扩展性,在数据集上无法发挥全部优势。(3)与ML-OFS-ANRS对比,两种算法在邻域处理均采取自适应的方法,保证了算法在不同数据都可最大化适应,在特征冗余筛选处理中,ML-OFS-ANRS依赖最大重要性标准,且针对不同数据集需要找出相应最优重要性阈值参数值,而所提方法采用模糊等价约束,模糊等价约束参数统一且特征冗余性参数设置依赖前一个已选特征子集数据,实现了自适应变化。(4)相比所提方法采用模糊等价约束进行特征冗余分析,ML-OFS-ANRS采用最大依赖和最大重要性标准进行特征冗余分析选择了更多的特征,造成一定的冗余。而在模糊等价约束下,可以考虑更多的候选特征进行特征冗余分析,使得最终所选特征子集最优。(5)图2给出实验过程中随着特征子集不断被筛选出来在数据集上的分类性能逐步提升。为保证实验效果图美观,仅展示了在Average Precision和Ranking Loss评价指标上的结果。可以看出在Birds和Yeast数据集上,所提方法分别筛选的特征子集数目达到50和35个左右时,表现出的分类性能趋于稳定。同特征子集数量下,所提方法在实验精度上优于另外两个对比算法。当其他算法特征子集筛选结果趋于稳定完成筛选,从实验精度上所提方法依旧领先。

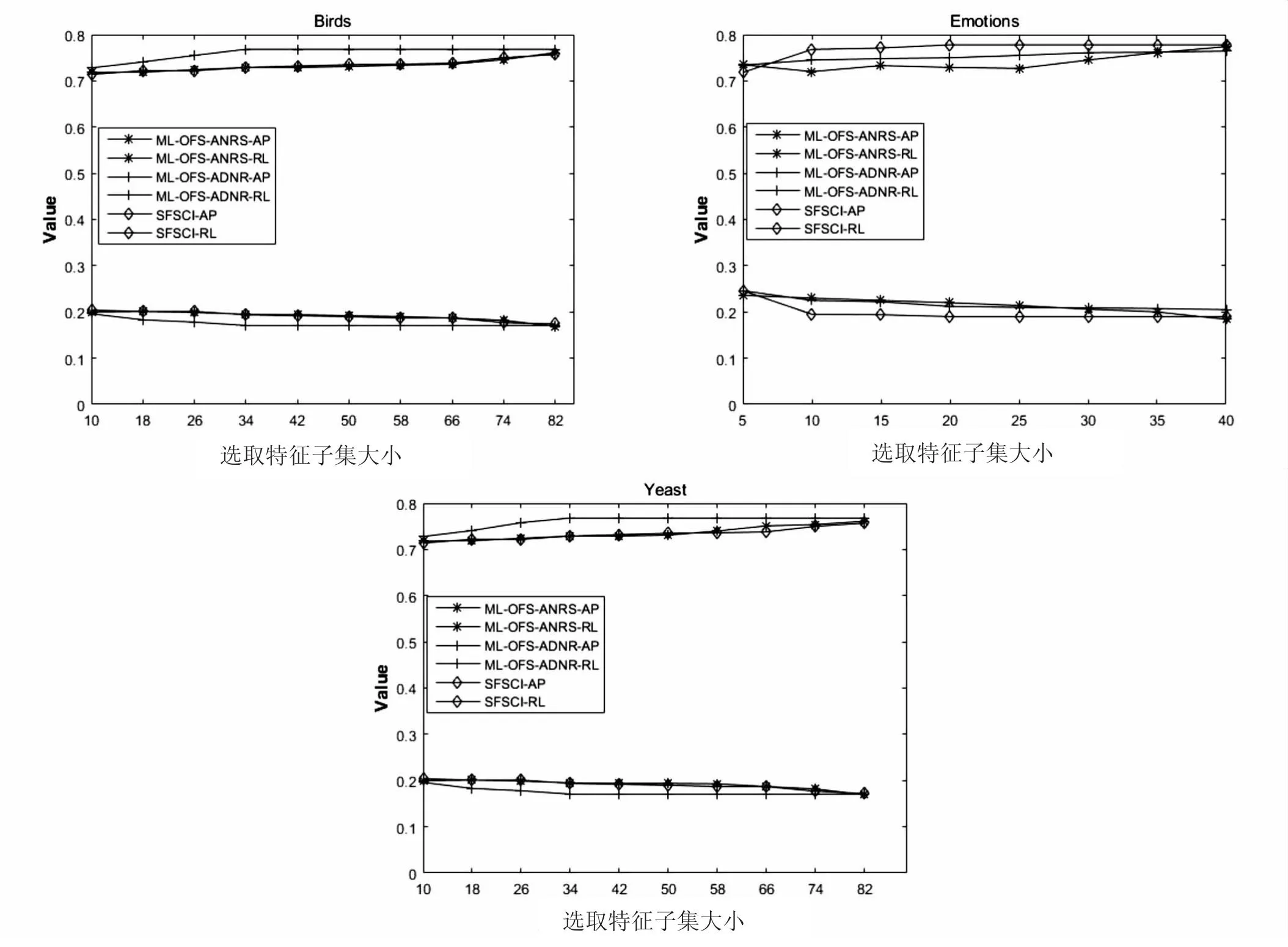
图2 在3个代表数据集上调整特征子集所得到的实验结果

4 结束语

提出一种基于密度邻域粗糙集的多标签流特征选择方法(ML-OFS-ADNR)。该方法参照单标签密度邻域关系理论在多标签分类环境中予以拓展,在依赖计算时根据周围实例的密度信息自动决定邻域数量,不需要预先指定任何参数。同时,采用模糊等价约束进行冗余分析,使所选特征子集小且具有鉴别性。与5种传统特征选择和2种流特征选择算法相比,该方法在相同特征数量的情况下优于传统特征选择方法,并在在线方式下优于流特征选择算法。未来的工作中,考虑实现模糊等价约束参数阈值自适应变化和模糊粗糙集理论应用流特征选择,实现更加精准、自适应无参化的流特征方法研究。