基于GWO-ELM模型的深基坑开挖变形预测研究

郭亚鹏，于 磊，田海川，朱洪宇，张 博，张 纯，董玉雄，马林杰

(北京市政路桥股份有限公司,北京 100000)

近些年来,随着社会经济的不断发展,地上资源已经不能满足人们的需要,城市建设逐渐转到地下发展[1]。由此,基坑的开挖面积和深度不断加大[2]。随着基坑深度的加大,基坑开挖施工的风险也逐渐升高[3]。因此,对深基坑开挖过程中的沉降变形进行控制和预测,为施工提供参考,从而有效保证施工安全,是当前的主要任务[4-6]。

针对深基坑的数值仿真分析和变形预测,国内外许多学者进行了大量的研究,取得了诸多成果。洪宇超等[7]采用CNN-LSTM组合神经网络对上海某深基坑地表进行预测,证明这种综合考虑时空特性的神经网络比单一LSTM神经网络预测结果准确。牛全福等[8]采取一种基于Kalman去噪的ARIMA-NAR神经网络组合模型进行预测分析。姜宇航等[9]提出针对于滑坡位移的(PSO-VMD)-NARX-GRU预测模型,精度明显高于静态模型中BP,SVM和ARIMA预测模型。张蓓等[10]利用权值参数以及梯度下降的方法对小波网络模型进行了优化和修正,并且工程实例证明,改进后的模型能使预测值更贴近于实测值。蒙国往等[11]对围护结构的水平位移采用BP神经网络滚动预测的方法,更贴合于实际工程。赵华菁等[12]以苏州某地铁车站深基坑工程证明了LSTM深度网络预测模型比BP神经网络预测模型具有更高的精度,更适用于预测地连墙变形问题。

综上所述,已有大量的学者通过采用有限元软件建模和神经网络预测的手段对基坑开挖变形规律进行了探究。但是由于各类误差的存在,对于深基坑开挖周围环境变形的预测有一定局限性。本文在前人研究的基础上,基于保定市汽车科技产业园深基坑工程大量监测数据,采用GWO-ELM预测模型对深基坑开挖地表沉降进行预测,为之后保定地区深基坑工程提供参考。

1 工程概况

1.1 工程背景

研究依托位于保定市的长城汽车科技产业园市政道路建设项目永华大街(南二环—太行路)排水工程顶管工作井。基坑开挖深度达到10.38 m,基坑周长约80 m。边坡采用80厚C20挂网喷射混凝土面层,面层插筋采用16@1 500×1 500 mm,插筋长度1.2 m,如图1所示。

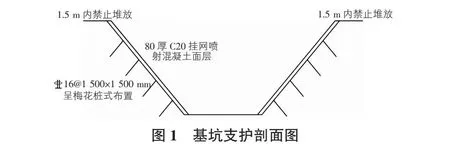
1.2 工程地质条件

土体的物理力学参数如表1所示。

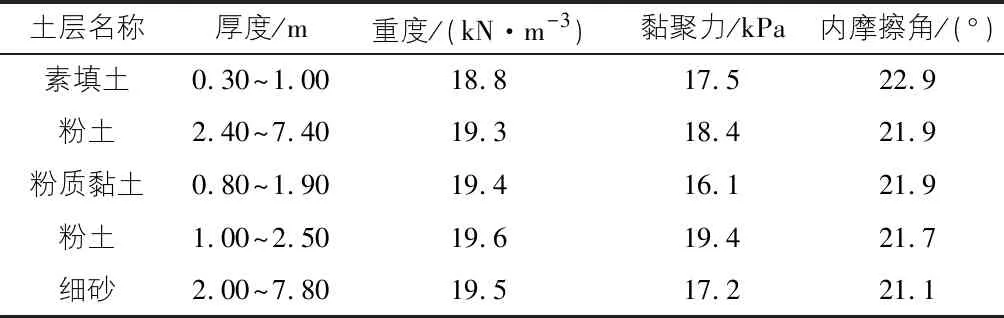
表1 土层物理力学参数

1.3 监测方案

为了确保深基坑工程及周边建筑物的安全,并给基坑施工提供参考,该工程对周边建筑物沉降、周边地表沉降、深层水平位移以及边坡土压力项目从施工开始到完成进行了监测,监测点的平面布置如图2所示。

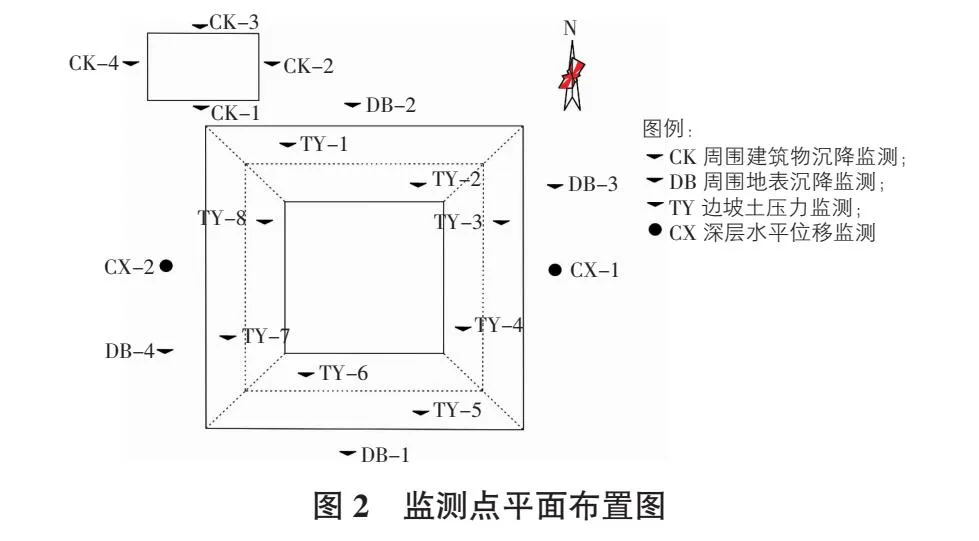
2 GWO-ELM神经网络模型

2.1 极限学习机模型

ELM是一种基于单隐层前向神经网络(SLFN)的训练方法[13],可以计算和分析网络的输出权重。具有很高的效率和学习速度。

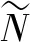
(1)

其中,oj为SLFN相对于输入样本xi的输出向量;ai=[ai1,ai2,…,ain]T和bi分别为第j个隐藏节点随机生成的学习参数;βi=[βi1,βi2,…,βim]T是第j个隐藏节点和输出节点的连接;f(xj;ai,bi)为原始ELM的激活函数。

设ai·xj为ai和xj的内积。等式(1)可以简洁的写为式(2):

Hβ=O

(2)

其中:

这里H被称为隐藏层的输出矩阵。

ELM理论声称,隐藏节点的学习参数ai和bi可以在不考虑输入数据的情况下随机分配。然后,等式(2)变为线性系统,输出权重β可以通过找到如下最小二乘解来解析确定(见式(3)):

(3)

其中,H+为隐层输出矩阵H的Moore-Penrose广义逆矩阵[14]。输出权重的计算是通过数学变换完成的,这避免了任何冗长的训练阶段,其中网络的参数是用一些适当的学习参数(如学习速率和迭代)调整的[15-16]。

因此,三步ELM算法可以总结如下:

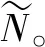
输出:输出权重β。

2.2 灰狼优化算法

GWO是一种具有强大搜索能力的新型元启发式算法[17]。目标函数最优解通过使用根据适应度值选择的三只狼(即α,β和δ狼)来定位,其他狼根据猎物的位置计算自己与猎物之间的距离[18-19]。

经过一代又一代,猎物的猎杀才得以实现。该算法的主要定义如下:

(4)

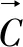
(5)

(6)

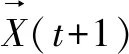
3)在捕食过程中,α狼、β狼和δ狼离猎物最近。第t代其他灰狼和这三只狼之间的距离可以根据等式得到。

(7)

(8)

捕食方向根据式(9)确定:

(9)

其中,k=α,β,δ,并且i=1,2,3。

3 工程应用

3.1 有限元模拟

3.1.1 模型边界条件确定

模型与实际工程等比例建立,基坑边长约为18.5 m。基坑外模型边长按照经验应取实际基坑边长的4倍～6倍,模型深度为实际深度的3倍～5倍,所以基坑外模型边长取60 m,深度取40 m。基坑支护采取喷锚支护的方式。对于模型的约束条件上,模型四周面约束其法向的位移,底部约束其三个方向的位移。

3.1.2 土体本构模型及网格的划分

本模型选择的是修正摩尔-库仑模型作为土体本构模型[20]。对比于普通的摩尔-库仑模型,修正摩尔-库仑模型模拟出的结果更贴切于深基坑开挖土体卸荷的过程。模型提取的结果主要集中在基坑模型附近,因此对这一部分的网格划分较细,本计算模型单元数12 460,节点数10 718。模型如图3所示。

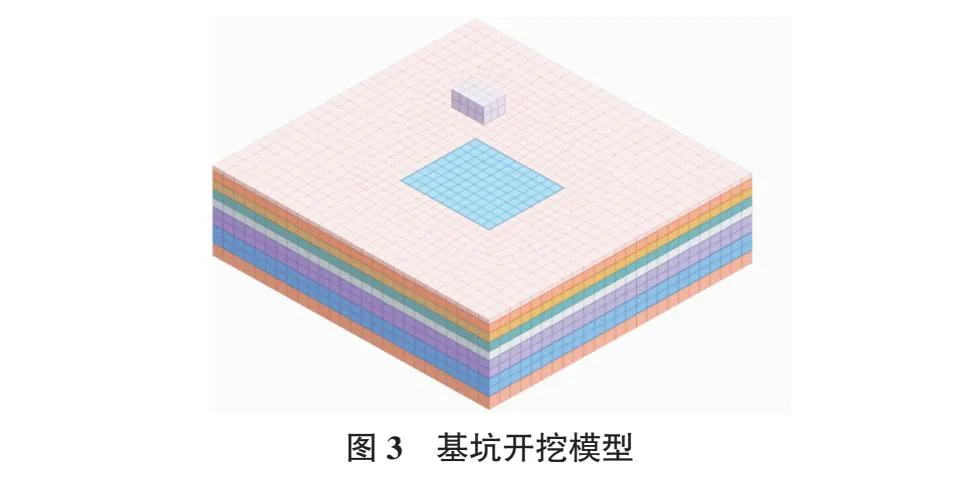
3.1.3 施工工况

开挖分为十步进行,见表2。开挖前,进行初始地应力的平衡,将Z方向的位移清零。

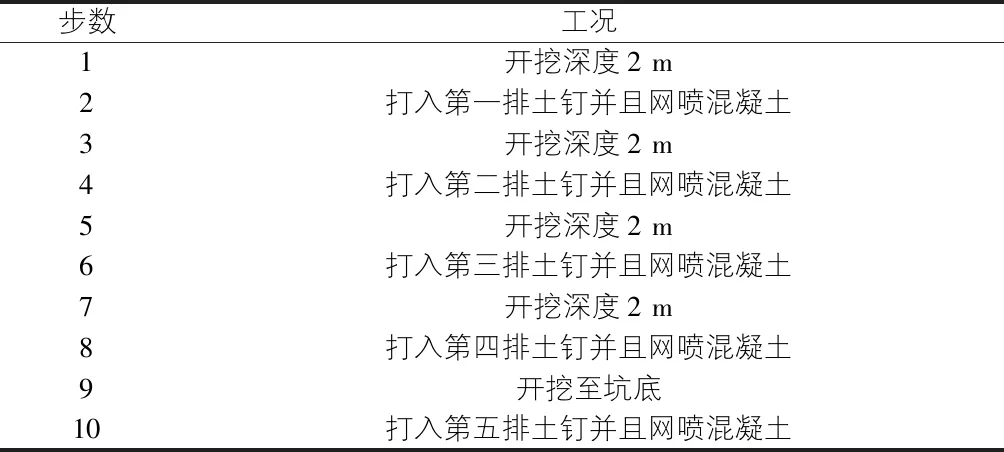
表2 施工工况

3.2 周围建筑物沉降分析

图4为基坑开挖部分工况的竖向位移云图,图5为周围建筑物沉降实测值与模拟值对比曲线。

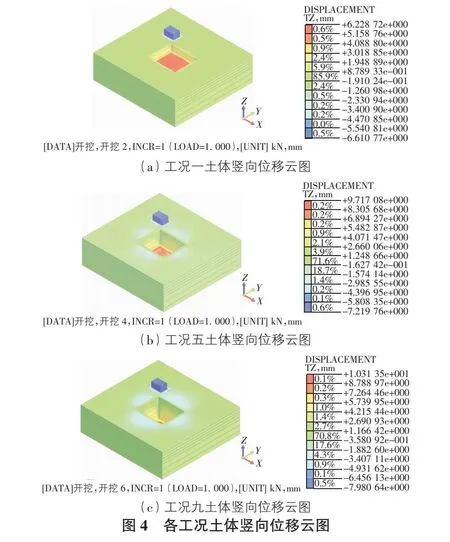
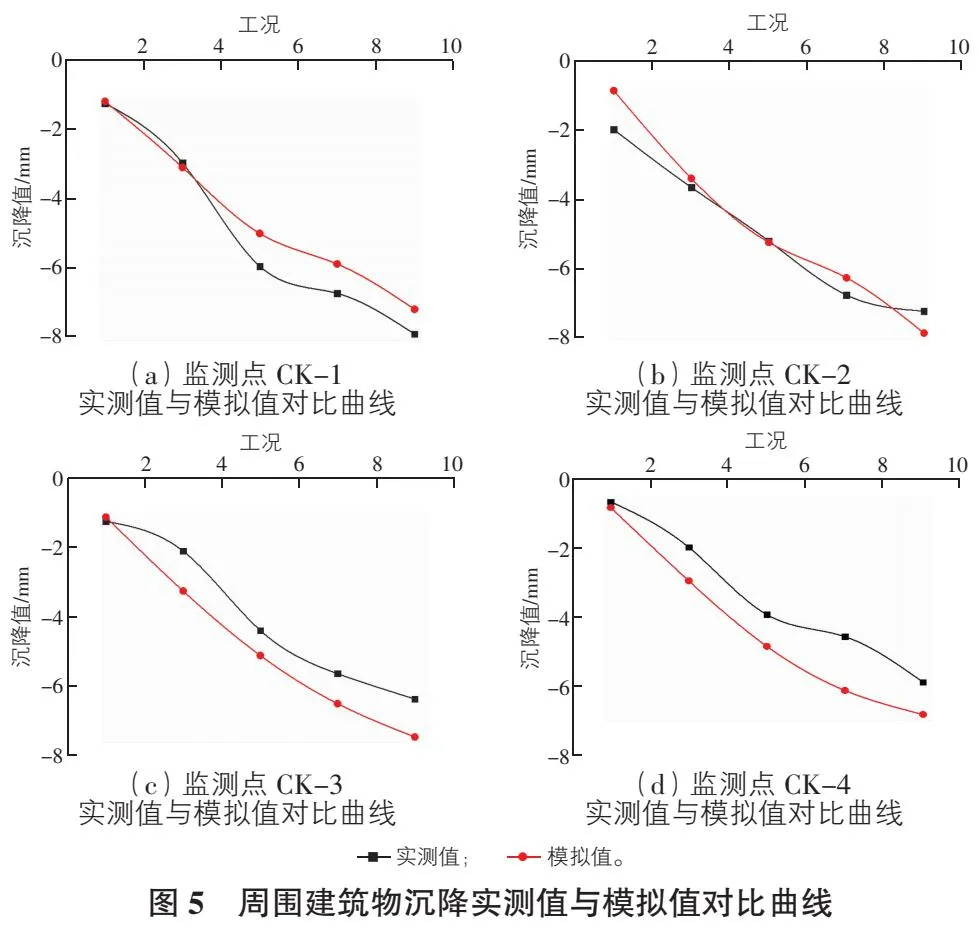
由图4,图5可知,随着施工的进行,基坑西北侧车库沉降逐渐加大。实际值变化曲线与模拟值变化曲线形态大致相同,但仍然存在一定偏差,总体来说模拟值要略大于实测值,可能是软件具有一定预警保护作用。监测点CK-1实测值要略大于模拟值,原因是监测点CK-1离基坑较近,受基坑开挖影响最大,有些临近荷载和周围施工的影响在软件中没有考虑到。实际监测的最大值为7.93 mm,有限元模拟的最大值为7.870 9 mm,均未超过预警值15 mm,表明支护结构施加及时有效。

3.3 深层水平位移分析

图6为基坑开挖部分工况土体深层水平位移云图,图7为开挖完成后土体深层水平位移实测值与模拟值对比曲线。

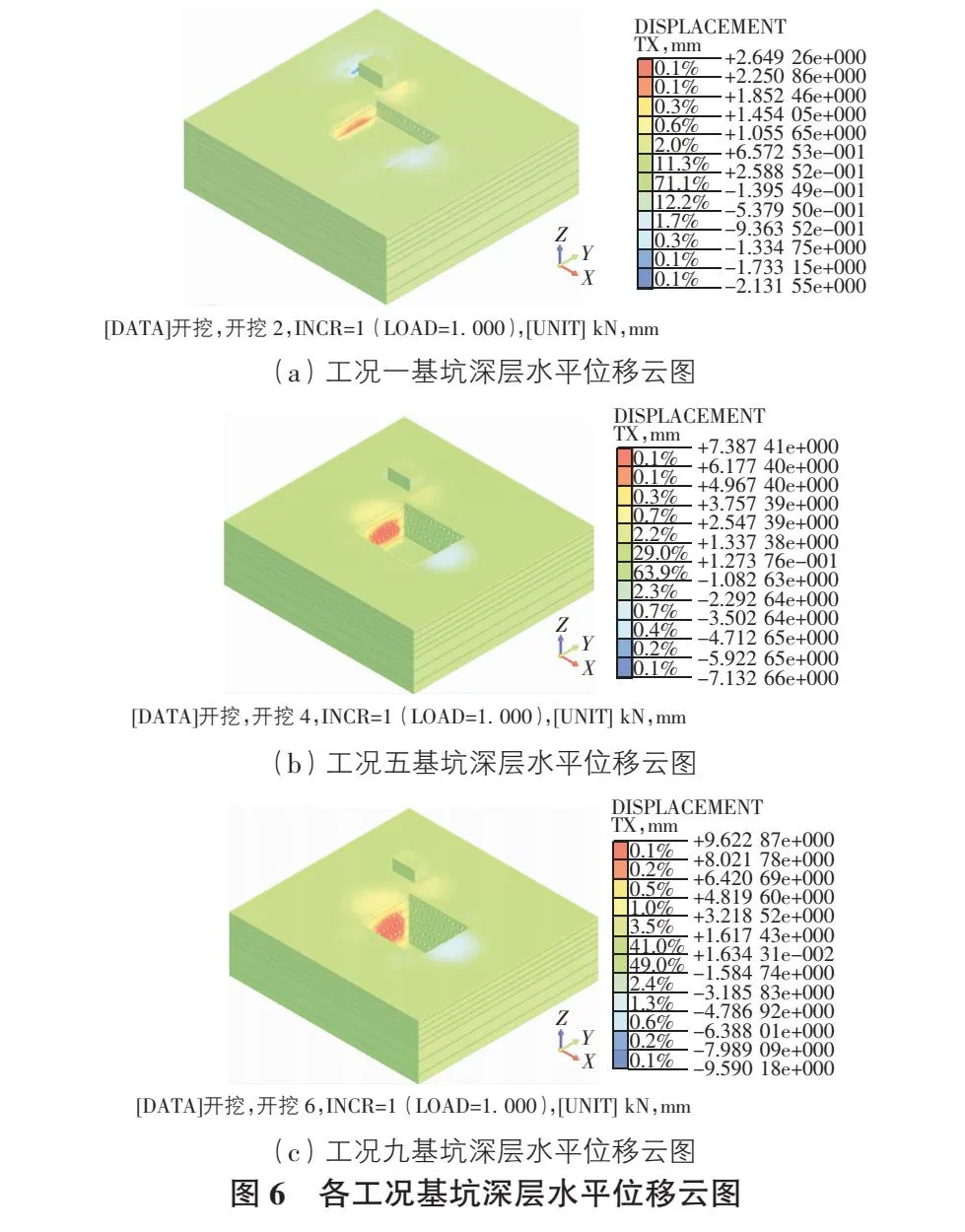
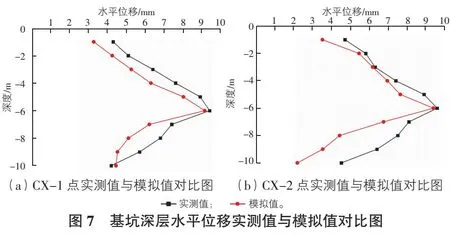
由图6可以看出,随着基坑的开挖,基坑侧壁各点都向着基坑内部移动,水平位移逐渐增加。并且同一工况各点的水平位移差值不超过10 mm。基坑侧壁最大水平位移位于边坡中部,并随着基坑开挖逐渐下移,开挖至坑底水平位移达到最大值。由图7可以看出,基坑深层水平位移实测值与模拟值整体趋势大致相同,均随着基坑深度的增加先变大后减小,但模拟值与实测值仍有偏差,其中最大差值为3.088 7 mm。模拟值整体小于实测值,原因是在模拟过程中没有考虑到机械振动、车辆流动等因素。

综上所述,本文从周围建筑物沉降和土体深层水平位移两个方面对比分析了实测值与有限元模拟值。从结果上看,模拟值仍与实测值有一定误差,但误差较小,可以作为神经网络的输入数据。

3.4 地表沉降预测

选取基坑北部监测点DB-2作为地表沉降预测点,以开挖深度、土钉数量及建筑物沉降作为输入因子,以监测点DB-2沉降值作为输出因子,建立神经网络数据集。具体预测过程如下:1)数据归一化处理。为消除数据量纲不同的影响,将开挖深度、土钉数量及沉降值预测归一化到[0,1]区间。2)模型参数设置。选取开挖深度、土钉数量、建筑物沉降作为影响因子,故输入层节点设置为3;模型输出为地表沉降值,故输出层节点数设置为1;隐含层神经元节点数设置为20。应用灰狼优化算法优化了ELM神经网络中的输入权重和隐藏层阈值。狼群大小为40个,迭代次数为100。同时,将结果与相同条件下未优化的ELM预测模型结果对比。3)模型预测结果分析。使用GWO-ELM预测模型得到地表沉降预测值,测试集结果如表3所示。监测点DB-2预测值对比图及误差曲线对比图如图8,图9所示。不同模型的预测精度如表4所示。

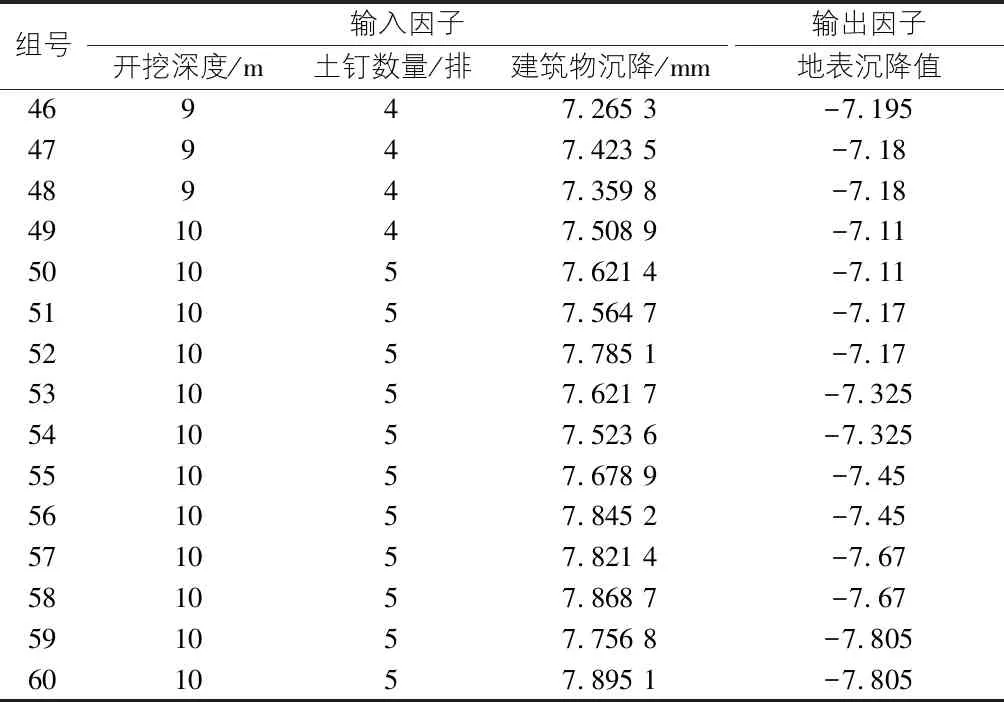
表3 神经网络测试集

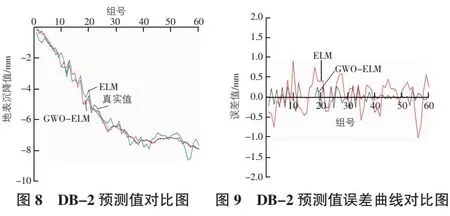
表4 模型精度对比

由图8,图9及表4可以看出GWO-ELM预测模型要优于ELM预测模型,在RMSE和MAE评价指标中,得到的均方根误差和平均绝对误差分别为0.312 58和0.261 45,相比于ELM预测模型更接近于实际地表沉降并且误差较小,判定系数R2=0.987 25,高于ELM预测模型,表面拟合效果较好,预测精度较高,具有相对可靠性。

4 结论

本文以深基坑地表沉降为研究对象,基于深基坑开挖过程中地表沉降预测精度问题,提出使用灰狼优化算法优化了极限学习机神经网络中的输入权重和隐藏层阈值,建立了GWO-ELM深基坑开挖变形预测模型。并以保定市汽车科技产业园深基坑工程进行验证,同时与未进行优化的ELM预测模型进行对比,得出了以下结论:1)本文以有限元模型开挖深度、土钉数量及周围建筑物沉降为输入因子,以地表沉降为输出因子,不同于以实际监测数据为样本,可以实现超前预测。2)以灰狼优化算法优化了极限学习机神经网络中的输入权重和隐藏层阈值,建立了GWO-ELM深基坑地表沉降预测模型,提高了预测模型的精度。3)本文以保定市汽车科技产业园深基坑工程证明,经过灰狼优化的极限学习机神经网络平均绝对误差为0.261 45,均方误差为0.312 58,R2=0.987 25,均优于未优化的极限学习机神经网络。