螺栓球节点对钢管杆件屈曲特征值的影响

吴志豪 ，张辰啸 ，贾冬云 ，王鸿宇 ，傅 阳

(安徽工业大学 建筑工程学院, 安徽 马鞍山243032)

随着钢结构的发展，空间网格结构因美观性较佳、施工安装便捷、造价低廉，越来越多地应用于实际工程[1]。作为一种广泛应用的结构形式，空间网格结构需有良好的整体性和承载力，才能保证结构在生产使用过程中不发生破坏。杆件屈曲对空间网格结构整体的稳定性和承载能力有重要的影响[2-4]，且在不同地震波的作用下，整体结构的稳定性对不同杆件屈曲位置有不同的敏感性[5–6]。因此，研究空间网格结构中杆件屈曲对分析空间网格结构的整体承载力和破坏特性有直接的参考价值。

为了研究杆件屈曲对整体结构的影响，国外学者设计一种可识别整体结构中杆件屈曲的有限元程序[7]，提出利用一种高阶单元预测杆件的屈曲荷载[8]和使用大位移非弹性分析的方法分析杆件屈曲和结构失稳的极限荷载[9]。螺栓球节点作为一种半刚性节点[10]常用于空间网格结构中杆件之间的连接，杆件屈曲特征值与杆件两端约束有密切的联系[11]。目前国内外学者多集中于螺栓球节点特性方面的研究，如刘红波等[12]研究不同温度下螺栓球节点的承载力；喻晓晨等[13]研究不同节点参数对节点刚度的影响并推导出考虑多参数影响的节点弯矩-转角曲线；Qiu 等[14]、Ding 等[15]、Tian 等[16]分别研究螺栓球节点中高强螺栓的疲劳性能、不同拧入深度时螺栓球节点的力学性能及螺栓球节点构件的超低周疲劳性能。现有研究对于螺栓球节点构件参数对杆件屈曲影响的关注较少，且未分析螺栓球节点的半刚性约束与杆件屈曲的关系。因此，利用ANSYS 软件建立螺栓球节点与杆件组合构件模型，研究螺栓球节点构件尺寸及中间杆件长细比等参数对组合构件屈曲特征值的影响，通过回归分析得到考虑半刚性节点参数和杆件长细比的屈曲特征值计算式。

1 螺栓球节点与杆件组合构件的有限元模型

1.1 几何模型

两侧螺栓球直径120 mm，高强螺栓直径16 mm，钢管杆件截面外径60 mm、内径53 mm、壁厚3.5 mm、截面惯性矩24.885 cm4，封板厚度14 mm，六边形套筒边长15.6 mm、长度30 mm，杆件两侧均有螺栓球节点。选取长细比分别为90，120，150，180，210，240 的6 种杆件，对应的杆件长度分别为1 800，2 400，3 000，3 600，4 200， 4 800 mm。

1.2 有限元模型的建立

螺栓球节点一般由螺栓、套筒、封板或锥头等部件组合而成，在工作时各部件之间的传力、滑移等使得螺栓球节点受力情况复杂。因此，杆件的螺栓球节点是一种复杂的约束，将其简单等效为刚接点或铰接点无法精确描述螺栓球节点的约束特性。考虑到两端螺栓球节点对杆件屈曲特征的影响，采用模拟接触法[17]建立有限模型，选用contact174 接触单元和target170 目标单元模拟各个面之间的接触。螺栓球节点施工安装时拧紧标准为销钉顶入螺栓表面深槽，无标准的预紧过程[18]，所以螺栓球节点有一定的预紧力，但预紧力大小未知，文中出于保守考虑不计入预紧力对杆件屈曲特征值的影响。

为了保证模拟的精确性，采用soild95 实体单元进行网格划分。长细比为150 的杆件有限元模型见图1，其中单元数为44 692 个、节点数为129 602 个，其余模型据杆件长度单元数和节点数在此基础上浮动。杆件、套筒以及封板材料为Q235B 钢材，弹性模量E为2.06×105MPa，泊松比为0.3；螺栓球材料为45#钢，弹性模量E为2.1×105MPa，泊松比为0.3；高强螺栓材料为40Cr 钢，弹性模量E为2.1×105MPa，泊松比为0.31[19]。

图1 螺栓球节点与钢管杆件组合构件有限元模型Fig.1 Finite element model of bolted ball joint and steel tubular component assembly

为使有限元软件接触算法快速收敛，在几何建模时将各构件接触面调整为刚好接触的状态并适当简化模型，将螺栓与螺栓球之间的接触设定为绑定接触代替螺纹间的互相作用，其他接触面的接触方式均设定为标准接触。有限元模型和几何模型会存在一定的偏差，某些接触面之间会出现微小的间隙和渗透，需通过调节接触选项中的关键项使KEYOPT(5)=3 闭合微小的间隙，消除接触面之间的渗透，将接触面调整至刚好接触。节点构件与接触设定见图2。

图2 节点示意图Fig.2 Schematic diagram of node

2 螺栓球节点与杆件组合构件的屈曲特征值分析

考虑螺栓球节点对杆件屈曲特征值的影响，在文中建立的有限元模型上施加合适的约束与荷载。在模型一端螺栓球表面节点施加XYZ3 个方向的约束；另一端螺栓球表面节点施加YZ方向的约束，保留沿杆件方向的自由度，并在螺栓球表面选取位于杆件轴线上的节点施加单位荷载，使中间杆件两端的约束和传力全部由螺栓球节点的接触提供，以实现考虑两端节点接触的杆件屈曲特征值计算。利用ANSYS 求解时，使用子空间缩聚法求得模型前五阶屈曲模态，并扩展求解结果。杆件长度为3 000 mm 时螺栓球钢管组合构件的计算结果和屈曲模态见图3。

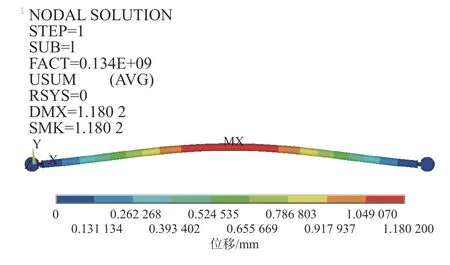
图3 螺栓球节点与钢管杆件组合构件的一阶屈曲模态Fig.3 First-order buckling mode of bolted ball joint and steel tubular component assembly

计算结果中接触面的设置是否合理需通过节点处的工作状态判断，接触面之间是否正常传力可通过节点螺栓与套筒的受力状态判断，套筒和螺栓的受力状态可通过应力分布情况判断，由此分析螺栓球节点在屈曲分析中是否符合螺栓球节点正常工作模式。杆件一阶屈曲模态下，螺栓球节点处套筒和螺栓的应力分布见图4，5。从图4，5 可看出：杆件屈曲时，节点处的套筒应力最大，套筒主要承受压力而螺栓主要承受屈曲时由于偏心产生的侧向力，这种工作模式和构件间的传力情况与螺栓球节点的实际工作状况[20]一致。

图4 套筒应力分布Fig.4 Sleeve stress distribution

图5 螺栓应力分布Fig.5 Bolt stress distribution

计算杆件屈曲特征值的欧拉公式[21]为

式中：Pcr为杆件两端固接时的屈曲特征值；E为杆件弹性模量；I为杆件截面惯性矩；L为杆件长度；µ为长度系数，用以考虑杆件不同约束对临界屈曲荷载的影响，杆件两端为铰接时 µ取1，固接时µ取0.5。

当两端螺栓球节点螺栓为M16 时，通过式(1)计算得到的杆件屈曲理论值与有限元计算值见表1。从表1 可看出：考虑杆件两端螺栓球节点接触的影响时，有限元计算的屈曲特征值处在两端铰接杆件与两端固接的杆件理论值之间，这是由于螺栓球节点是一种半刚性节点，约束的效果弱于固接约束，强于铰接约束；随着杆件长细比的增加，螺栓球节点有限元计算值与固接时的理论值越接近，对应的 µ值越接近固接时的值，表明杆件长细比越大螺栓球节点对杆件的约束能力越强。

表1 杆件的屈曲理论值与有限元计算值Tab.1 Theoretical and finite element calculated values of buckling for the component

3 螺栓球节点对杆件屈曲特征值影响的参数化分析

3.1 螺栓头半径对杆件屈曲特征值的影响

螺栓头是将拉力传递给螺栓的主要接触面，通常螺栓头半径会随螺栓半径的不同而改变，螺栓头与封板接触面的大小取决于螺栓头半径大小。在螺栓半径为8 mm、套筒壁厚为5.5 mm、套筒长度为30 mm、封板厚度为14 mm 的条件下，模拟分析传力面对杆件屈曲特征值的影响，结果如图6。

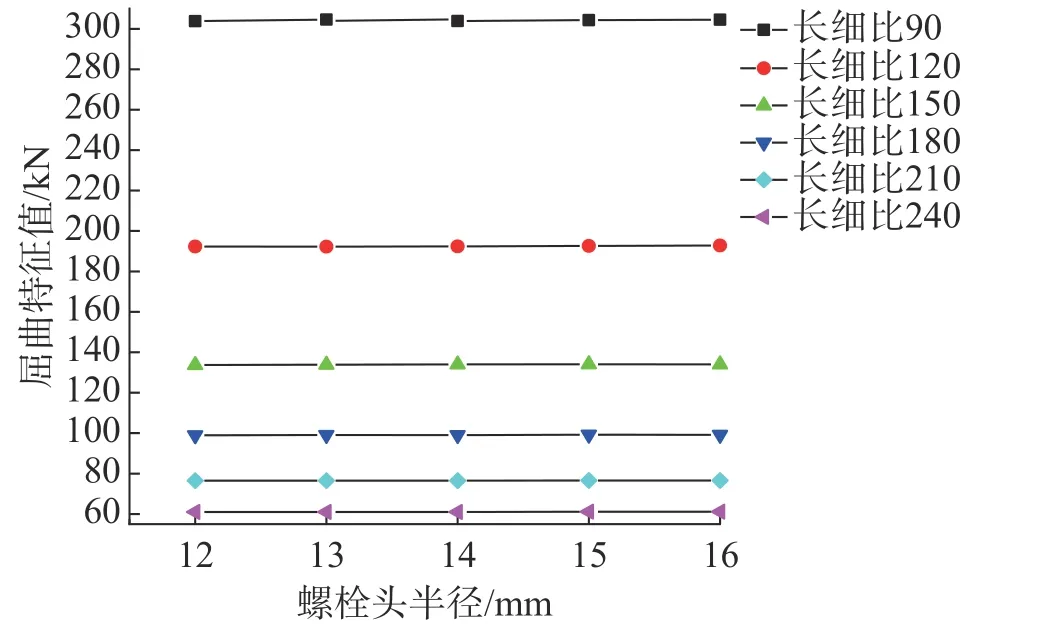
图6 螺栓头半径对屈曲特征值的影响Fig.6 Effect of bolt head radius on flexural eigenvalues

从图6 可看出：随螺栓头半径的增加，杆件屈曲特征值几乎不变，表明螺栓头半径对杆件屈曲特征值几乎没有影响。这是因为在计算杆件屈曲特征值时，螺栓头与封板之间仅传递很小的拉力，主要受力构件依次为套筒、螺栓，与封板不同，螺栓头在屈曲分析计算中基本不主动传力，接触面的力是由于杆件屈曲使得螺栓球节点有一定转角后才有接触和力的传递，所以此处的传力面积对杆件屈曲特征值的影响可忽略不计。

3.2 螺栓半径对杆件屈曲特征值的影响

高强螺栓是螺栓球节点的主要连接构件，对节点性能有显著影响。由上文知螺栓头半径对钢管杆件屈曲特征值几乎无影响，故取螺栓头半径4 mm，在套筒壁厚5.5 mm、封板厚度14 mm、套筒长度30 mm 时，模拟分析螺栓半径对杆件屈曲特征值的影响，结果如图7。从图7 可看出：杆件屈曲特征值随螺栓半径的增加而增加，两者几乎呈线性关系。这是因为螺栓半径增加时螺栓球节点的刚度增加，致使杆件屈曲特征值增加。因此，可通过加大螺栓球节点的螺栓半径增强螺栓球节点的刚度来提升杆件承载力。从图7 还可看出，螺栓半径对杆件屈曲特征值的影响随杆件长细比的增加而逐渐减小。

图7 螺栓半径对屈曲特征值的影响Fig.7 Effect of bolt radius on flexural eigenvalues

3.3 套筒壁厚对杆件屈曲特征值的影响

在螺栓半径为8 mm、封板厚度为14 mm、套筒长度为30 mm、螺栓头半径为12 mm 时，套筒壁厚(取套筒最薄处的厚度为套筒壁厚)对杆件屈曲特征值影响的有限元分析结果如图8。

图8 套筒壁厚对屈曲特征值的影响Fig.8 Effect of sleeve wall thickness on flexural eigenvalues

从图8 可看出：杆件屈曲特征值随套筒壁厚的增加而增加，随杆件长细比的增加而增速下降，表明套筒壁厚对杆件屈曲特征值的影响较大。安装螺栓球节点时套筒易更换，故在实际工程中需增大杆件屈曲特征值时，增加套筒厚度相较于增加螺栓半径便捷。

3.4 封板厚度对杆件屈曲特征值的影响

封板是螺栓球节点的重要传力构件，所有的轴力和侧向力都经由封板传递至套筒和螺栓杆。螺栓球节点螺栓半径8 mm、套筒壁厚5.5 mm、套筒长度30 mm、螺栓头半径12 mm 时，封板厚度对杆件屈曲特征值的影响如图9。从图9 可看出：杆件屈曲特征值随封板厚度的增大而增大，但增幅不大，封板厚度对杆件屈曲特征值的影响较小。这是由于封板厚度增加，只增大了侧向力传递面的面积，对螺栓球节点的刚度几乎没有影响。

图9 封板厚度对屈曲特征值的影响Fig.9 Effect of seal plate thickness on flexural eigenvalues

3.5 套筒长度对杆件屈曲特征值的影响

螺栓球节点处的高强螺栓会配置不同长度的套筒，套筒长度对螺栓球节点的刚度也有一定影响。螺栓半径8 mm、套筒壁厚5.5 mm、封板厚度14 mm、螺栓头半径12 mm 时，套筒长度对屈曲特征值影响的有限元分析结果如图10。

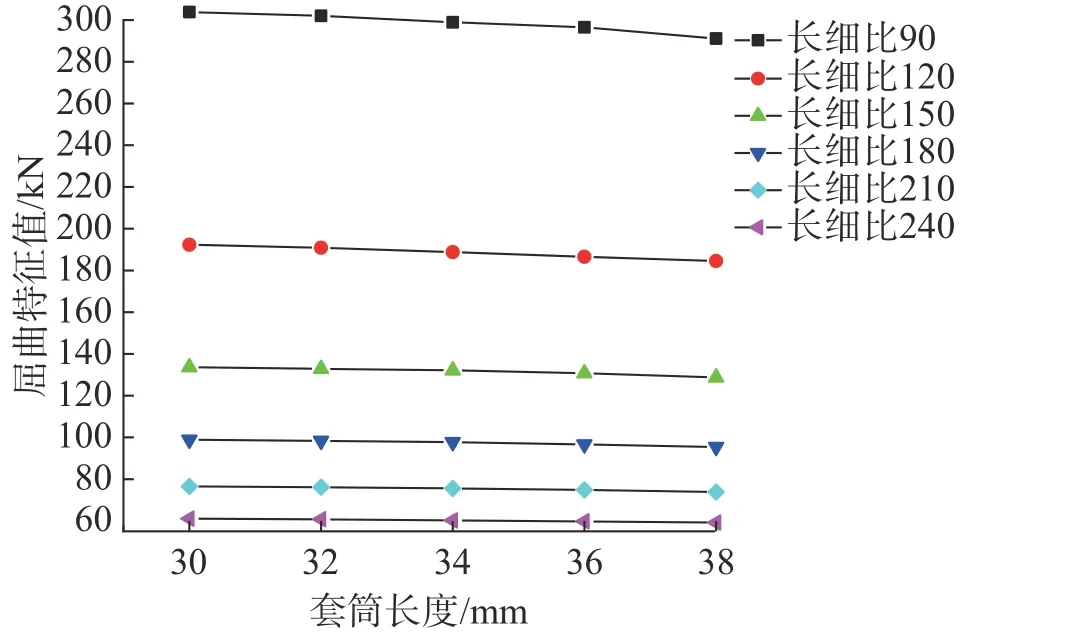
图10 套筒长度对屈曲特征值的影响Fig.10 Effect of sleeve length on flexural eigenvalues

从图10 可看出：杆件屈曲特征值随套筒长度的增大而下降，这是由于在其他参数不变的情况下增加套筒长度使螺栓长度增加，螺栓球节点的刚度下降，节点对杆件的约束能力下降，从而杆件屈曲特征值下降；随杆件长细比的增加，杆件屈曲特征值的降幅越来越小，套筒长度增加对其的影响逐渐下降。总体看，套筒长度对杆件屈曲特征值的影响较小。

4 组合构件屈曲特征值的回归分析

由前文分析可知螺栓球节点约束处在固接约束和铰接约束之间，因此可将螺栓球节点的约束看作削弱的固接约束，削弱系数 α=P/Pcr，P为考虑螺栓球节点影响有限元计算的屈曲特征值。鉴于螺栓头半径对杆件屈曲特征值几乎无影响，故不考虑螺栓头半径因素，考虑其他因素建立回归方程：

式中：β0，β1，β2，β3，β4，β5为常数；x1为长细比；x2为螺栓半径；x3为套筒壁厚；x4为封板厚度；x5为套筒长度。利用最小二乘法求得式中β0，β1，β2，β3，β4，β5的值，得到回归方程：

为验证该回归方程的准确性，以螺栓半径为8，9 mm 的2 组数据为例，将有限元计算值代入α=P/Pcr，计算得出的削弱系数α 与式(3)的拟合值见表2。表2 中相对误差为α 的拟合值与计算值的差值除以α 的拟合值。

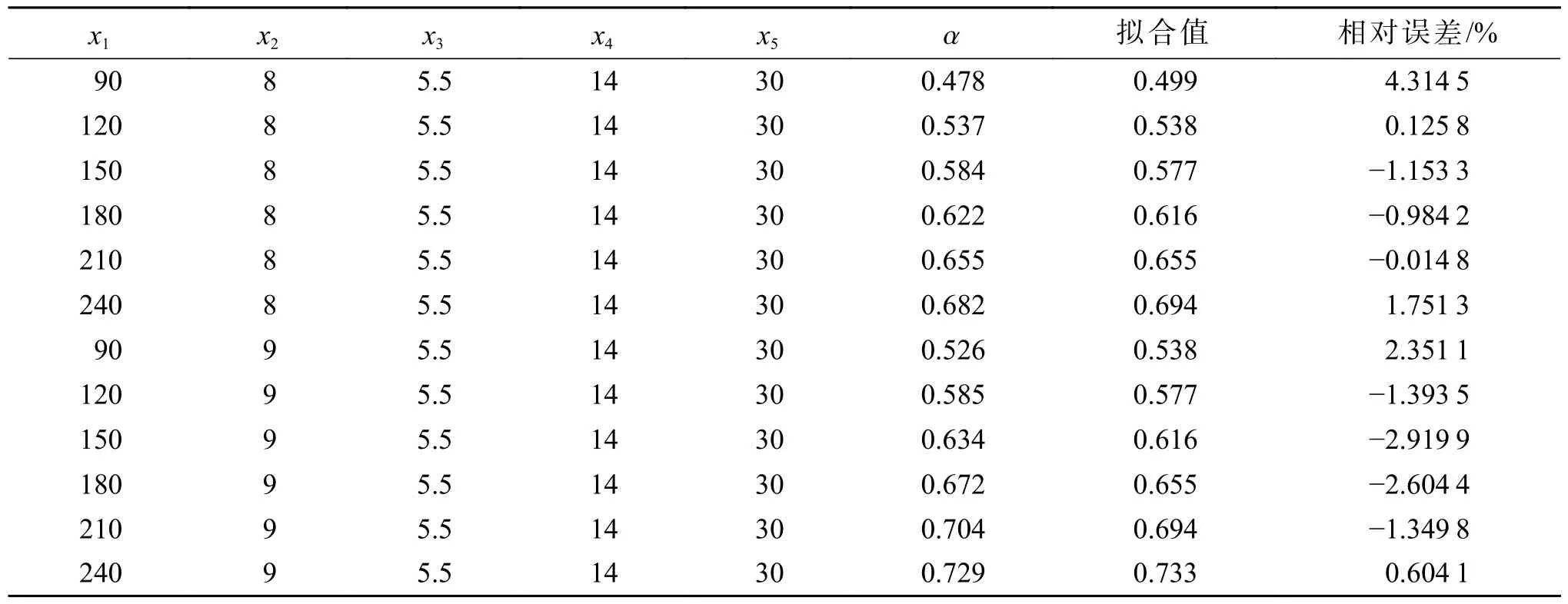
表2 削弱系数与回归公式拟合值对比Tab.2 Comparison of attenuation coefficient and regression formula fitting value

从表2 可看出，有限元计算值与回归方程计算值的相对误差均小于5%，两者得到的计算值相差不大。由MATLAB 计算得出本文确定系数R2为0.98(大于0.95)，证明了回归方程式(3) 的准确性。由式(3)，(1)得到考虑螺栓球节点影响的杆件屈曲特征值计算式：

式(4)较复杂，难以在实际工程中应用。将上文研究的构件屈曲特征值影响因素分为两类：将杆件自身长细比作为一个影响因素，将螺栓半径、套筒壁厚、封板厚度和套筒长度等节点尺寸作为另一类影响因素。利用MATLAB 与Excel 对数据进行处理后发现，可将螺栓球节点的4 个影响因素统一为一个影响因素，称为节点综合参数η，计算公式为

将式(4)中削弱系数替换为式(7)后，该回归公式可表达为

以螺栓球节点综合参数η 为X轴，杆件屈曲特征值为Y轴绘制有限元计算屈曲特征值的散点图，且与式(8)对应拟合值的曲线进行比较，结果如图11。

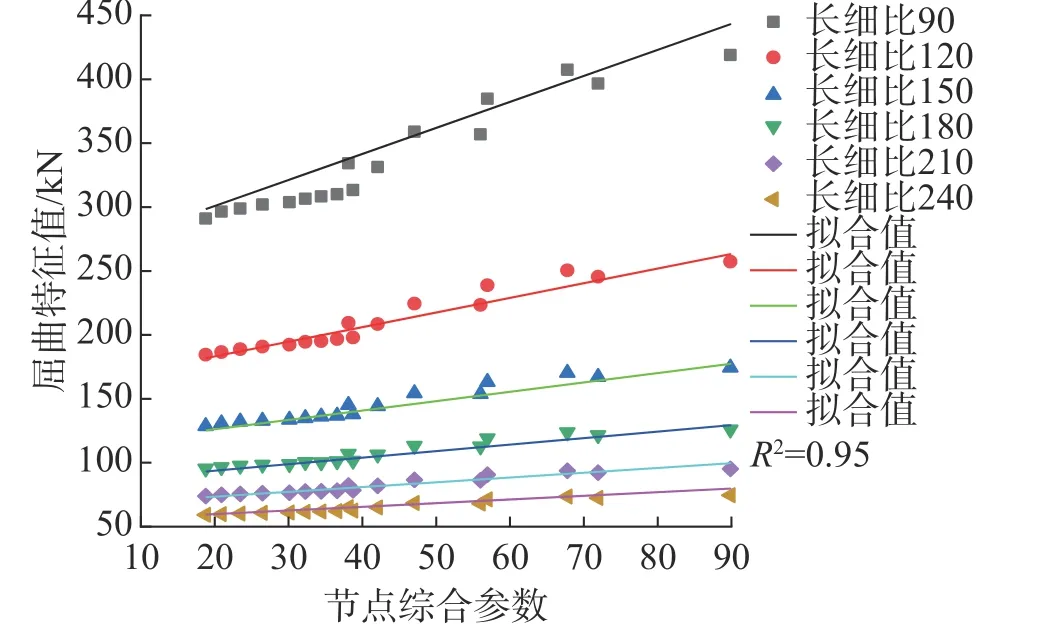
图11 屈曲特征值拟合曲线Fig.11 Buckling eigenvalue fitting curves

从图11 可看出：屈曲特征值随节点综合参数的增大而增大；节点综合参数对屈曲特征值的影响随长细比增大而减小。长细比较大时拟合值与有限元计算值偏差较小；长细比较小时拟合值与有限元计算值出现一定的差异，但总体趋势一致，说明式(8)能够较精确地计算屈曲特征值，确定系数R2为0.95，精确性可达到要求，可用于实际工程计算。

5 结论

利用ANSYS 软件对螺栓球节点与钢管杆件组合构件进行有限元建模，分析螺栓球节点构件尺寸对中间杆件屈曲特征值的影响，通过回归分析获得组合构件的屈曲特征值计算式，得到以下主要结论：

1) 螺栓半径、套筒壁厚对杆件屈曲特征值的影响较大，随两者的增加杆件屈曲特征值有所增加；杆件屈曲特征值随封板厚度、螺栓头半径的增加而增大，但螺栓头半径对杆件屈曲特征值的影响可忽略不计；杆件屈曲特征值随套筒长度的增加而减小。此外，随杆件长细比增加，上述几种因素对杆件屈曲特征值的影响均逐渐减小。

2) 确定了半刚性节点对于杆件屈曲特征值的削弱系数，提出了考虑半刚性节点影响的杆件屈曲特征值计算式，该式相较于传统计算方法考虑了半刚性节点不同构件尺寸的影响，能够较好地预测螺栓球节点与钢管杆件组合构件的屈曲特征值。

文中对于螺栓球节点与钢管杆件组合构件的有限元屈曲特征值分析，未考虑材料非线性及几何非线性的屈曲分析，对于材料、几何非线性对组合构件失稳荷载的影响还需进一步研究。