长三角港城协调水平对城市经济增长影响的空间效应研究
方 惠 ,常志朋
(安徽工业大学 商学院, 安徽 马鞍山 243032)
我国进入新发展时代,统筹融合推动联运高质量发展,港口和城市的协调发展是极为重要的一项发展任务,协调好港城关系对港口城市的可持续发展意义重大[1]。随着长三角地区产业结构的转型升级、港口资源整合和港区功能的不断调整以及城市对运输等要求持续提高,需进一步探究长三角港城关系及其对城市经济增长影响的空间效应,以促进长三角港口和港口城市经济持续高质量发展。
1 理论分析与研究假设
近年,随着我国经济发展从重“速”转变为重“质”,港城关系逐渐演变为相互融合、协同共进的系统共同体。初期,港口作为城市的“运输中转站”起到先导和驱动作用,同时兴起向前向后的相关产业,为城市提供配套服务、就业岗位、贸易机会等红利,城市经济借机不断提升[17];中期,城市开始对港口提供支撑,港口的基础建设、相关人才、资金需求得到满足,2 个子系统更多呈现相互正向反馈关系,形成良性循环[18];后期,港城关系出现瓶颈,港口发展缺乏深水航线、深水岸线,难以满足国际大型船舶的发展趋势,而城市经济结构较为固定,港口发展同步的产业结构优化升级等问题逐步凸显[19]。港城关系发展出现较为明显的不匹配,损耗了港城系统发展的效率,港口发展受到限制,城市经济增长也受到影响。
港城协调水平对城市经济增长的影响涉及增长极理论和外部性理论。增长极理论认为,经济增长通常是从“增长中心”向其他地区传导,从而影响整个区域经济增长,应选择特定的“增长中心”作为增长极,带动区域经济发展[20]。外部性指经济主体对其他主体产生一种外部影响,包括正外部性和负外部性[21]。在港城关系中,城市依靠港口功能及港航业实现快速发展,港口依赖城市经济、人才、科技的支撑,体现正外部性;但城市由于自身发展而挤占港口用地、工业排水等,造成港口作业拥挤、水域污染等问题,同时港口运转对城市的噪音污染、生态破坏等属于负外部性。因此,长三角地区港城协调发展是否能够作为“增长中心”,对城市经济增长起到积极作用,有待实证考察。
基于以上分析,提出理论假设:在控制其他变量的前提下,长三角港城协调发展对城市经济增长具有空间溢出效应。
2 研究对象与数据来源
将长江三角范围内的41 座城市及港口作为研究对象,但在收集、整理数据过程中,发现宁波市和舟山市港口于2006 年合并、部分港口建成通航时间晚于本文研究的起始时间以及部分小型港口的数据统计不全、无处求证等问题。考虑以上情况,选取33 个主要港口为研究对象,具体如表1。

表1 长三角主要港口Tab.1 Major ports in the Yangtze River Delta
基于长三角主要城市与港口的数据,评估2011—2020 年长三角港口及城市的发展状况。研究过程中港口相关5 项指标数据来自《中国港口年鉴(2011—2020)》,城市相关7 项指标数据来自2011—2020 年各城市统计年鉴、《中国交通运输年鉴(2011—2020)》。
3 计量模型与实证分析
3.1 港城协调水平测度
3.1.1 测度指标体系的选取与构建
刘厂长说,企业有了问题对你们政府官员也不利,即便不追责,别人也会说你们领导无能。你还年轻,出头的日子在后头,干革命工作不要太较真儿,不能操之过急,恨不得像我一样结婚就生娃。有些事只能大事化小,小事化了。工作中要多积累政绩,要注重成效,要像这门楼一样有与众不同的地方。再说,企业经营行为与政府工作不可同日而语,即使都是在追求最大效益,效益的概念也不尽相同。他一直用一种不阴不阳又充满自信的口吻教训我,俨然他是我的上级领导。也是,像我们突击从教育部门选拔的干部要进入行政管理角色确实还需要一个适应过程,至于企业管理更要在实践中重新加强学习。
根据可得性、科学性等原则,从港口设施条件和港口运营规模层面对港口子系统进行综合实力评估;选择城市经济规模、城市外向能力层面评价城市子系统,保留临港产业特色指标,对港口城市进行综合评价。借鉴已有研究成果[22],构建的评价指标体系如表2,由熵权法处理得到表中各指标权重,部分数据不全采取插值法补充。
3.1.2 测度模型的建立
港城协调度是度量港口和城市良性互动关系的定量测度指标,分为静态、动态协调度。为对港城协调水平进行准确的测度,建立两者结合的协调度模型进行综合考量。
1) 静态协调度模型。根据表2 所示指标权重,分别计算第i个港口子系统综合评价指数S1、城市子系统综合评价指数S2。
其中: σ为 港 口子系统的某个指标;h为城市子系统的某个指标;wσ为港口子系统各项指标的权重值;riσ为港口子系统每项指标标准化后的数据;vh为城市子系统每项指标的权重值,gih为城市子系统每项指标标准化后的数据。
耦合在物理学中是指2 个或2 个以上的体系通过相互作用而彼此影响以至联合起来的现象,文中将物理耦合的模型引入测度长三角港城静态协调水平,其计算公式为:
其中:C为耦合度;D为静态耦合协调度;T为港城协调水平的综合发展指数;a和b为各个子系统的权重,且a+b=1,一般认为港口与城市同样重要,因此设定a=b=0.5。根据均匀函数分布法划定的标准(表3) 确定静态耦合协调度的类型,D的取值范围为0~1。

表3 静态协调度的划分标准Tab.3 Classification standard of static coordinationdegree
2) 动态协调度模型。动态协调度能够反映2 个子系统协调状况的发展趋势,表达式为
其中:Dd为动态协调度;Dt为t时刻港城静态协调度;Dt-1为t-1 时刻港城静态协调度,动态协调度划分为以下标准进行判断,如表4。

表4 动态协调度的划分标准Tab.4 Classification standard of dynamic coordinationdegree
3.1.3 测度结果与分析
由式(1)~(5)计算长三角沿海港城协调度,通过ArcGIS 软件制图可观察到2012—2020 年主要年份长三角各港城静态协调水平空间差异及变化,如图1。2012—2020 年长三角港城动态协调度如表5。

图1 主要年份长三角港城协调水平Fig.1 Coordination level of ports and cities in the Yangtze River Delta in major years

表5 2012—2020 年长三角港城动态协调度Tab.5 Dynamic coordination degree of ports and cities in Yangtze River Delta from 2012 to 2020
由图1 可看出,2011—2020 年长三角地区港城协调水平迅速发展。从增速看,安徽省亳州市的港城协调水平涨幅明显,江苏省盐城市、扬州市的协调水平也增长迅速,但安庆市、常州市的港城协调水平无明显增长。从区域角度来看,截至2020 年长三角地区达极度协调水平的港城仅1 个、高度协调港城2 个、中度协调港城6 个、低度协调港城数量最多为18 个、极低协调港城6 个均在安徽地区,其中苏浙皖交界处港城协调水平有跨越性提升,空间差异明显。引入动态协调度分析(表5),从动态发展角度看,区域整体动态协调度基本稳定在1 以上,说明港城协调水平正逐年优化。安徽省亳州市、六安市、阜阳市的港城动态协调度年均最高,虽仍处于低度协调水平,但发展潜力可观;安庆市的港城动态协调度小于1 的年份最多,这可能是由于城市、港口发展水平均未出现显著提高,港城协调水平未能得到明显提升。
总的来说,2011—2020 年期间,随着长三角一体化水平不断提升,长三角绝大部分港城协调关系在逐步改善,在积极发展港口产业的前提下,城市经济和港口能级都在迅速提升,但整体仍处于较低协调水平。近年外部环境的复杂和产业结构的调整导致港口的不稳定发展、港口发展过程中出现的追求规模扩大和城市无序竞争等因素都在一定程度上限制了港城协调水平;同时恶意竞争、政策倾向、港城发展不匹配等问题也会造成港城协调水平的较大差异,港城协调水平与城市经济增长具有明显空间差异,但两者之间的空间效应还需进一步研究。
3.2 空间效应实证分析
3.2.1 变量选取与相关检验
1) 变量选取。考虑到人均国内生产总值(gross domestic product,GDP)是城市经济指标核算的核心,选择人均GDP 代表城市经济增长指标,参考范厚明等[11]的研究,将港城静态协调度作为外生变量引入(简称港城协调度);依据《长江三角洲区域一体化发展规划纲要》对城市经济增长的规划及经济学原理,确定其他控制变量,各变量符号及说明如表6。
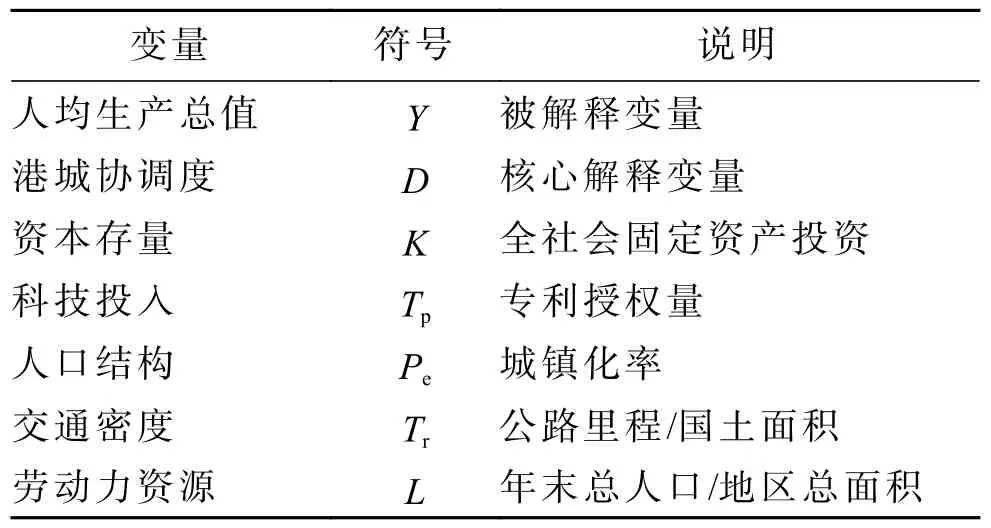
表6 变量符号及说明Tab.6 Variable symbols and descriptions
2) 平稳性检验。为避免出现“伪回归”现象,选取LLC 和ADF 对各变量进行平稳性检验,同时通过两类检验判定该序列是否平稳,未通过检验的原序列进行一阶差分后再次检验,结果如表7。

表7 单位根检验结果Tab.7 Unit root test results
3) 协整检验。经过一阶差分后各变量均为同阶单整,需进一步进行协整检验来检测各变量之间是否具有长期稳定关系。在协整检验方法中,Pedroni检验和Kao 检验对于本文具有适用性,故采取该方法进行检验,结果如表8。表8 显示各变量均存在协整关系,可构建模型来验证变量关系。

表8 协整检验结果Tab.8 Results of cointegration test
3.2.2 空间模型选取与构建
1) 空间相关性分析。采用Moran’sI指数对空间相关性进行分析,观察区域总体的空间相关性及区域内空间集聚特征,结果如表9。
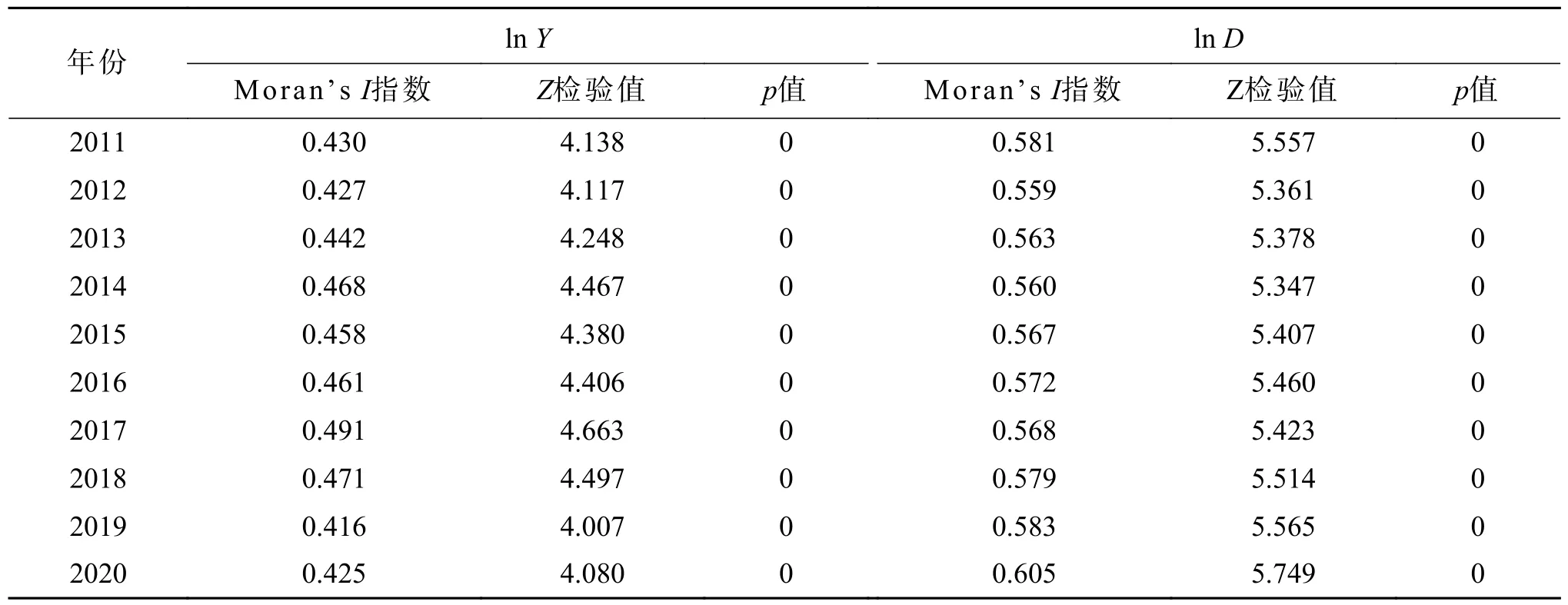
表9 长三角城市经济及港城协调度的全局Moran’s I 指数Tab.9 Global Moran’s I index of urban economy and port city coordination degree in Yangtze River Delta
由表9 可看出:2011—2020 年长三角港口城市经济及港城协调度的全局Moran’sI指数均为正数,且均在1%的水平下显著。说明城市经济增长、港城协调水平均存在较强的空间相关性,也存在空间聚集的趋势。
2) 模型选取与构建。长三角港城协调度与城市经济在空间上存在显著的正相关性,因此选择空间计量方法更科学准确。空间计量模型包括3 种形式:空间滞后模型(spatial lag model,SLM),探究的是因变量之间的内生交互效应,在空间依赖性极强的情况下,自变量均可借助空间传导机制直接作用于因变量;空间误差模型(spatial error model,SEM),探究的是误差项之间的交互效应,认为空间相关性是由误差项引起的;空间杜宾模型(spatial Dubin model,SDM),同时包含空间滞后和空间误差影响,可同时体现外生交互效应和内生交互效应。SLM,SEM,SDM 的基本结构分别为:
其中:i,j为样本个体,指第i,j个港口;t为时间; α为常数项参数; ρ为空间回归系数,反应其他地区解释变量对本地区被解释变量的作用;wij为空间权重矩阵,本文所用空间权重矩阵为地理邻接矩阵,城市接壤取1,不接壤则取0; β为解释变量的回归系数,反应本地区解释变量对本地区被解释变量的作用;X为解释变量; µ为空间效应; λ为时间效应; ε为残差项; φ为随机误差项; θ为未知参数。
为选取合适的空间计量模型,经LM 检验,显示空间滞后模型的LM 统计量和空间误差模型均显著,但空间误差模型的Robust-LMERR 统计量比空间滞后模型的Robust-LMLAG 统计量更显著。根据LM检验结果,空间误差模型更合适。空间滞后模型与空间误差模型均是一种特殊的空间杜宾模型,可验证空间杜宾模型是否可以退化成空间滞后模型与空间误差模型,空间滞后模型与空间误差模型的Wald检验统计量、LR 检验统计量均强烈拒绝原假设,故选择空间杜宾模型。本文构建的空间杜宾模型如下:
3.2.3 空间效应实证结果与分析
经Hausman 检验强烈拒绝随机效应模型(模型4)的原假设,对空间杜宾模型采取固定效应估计。利用STATA13 分别对时间固定(模型1)、空间固定(模型2)和双向固定(模型3)效应进行不同形式的空间面板杜宾模型估计,发现时间固定模型(模型1)更适合(表10)。构建包含时间固定效应的空间面板杜宾模型,对模型中的直接效应和间接效应进行分解,各变量对城市经济的效应分解如表11。
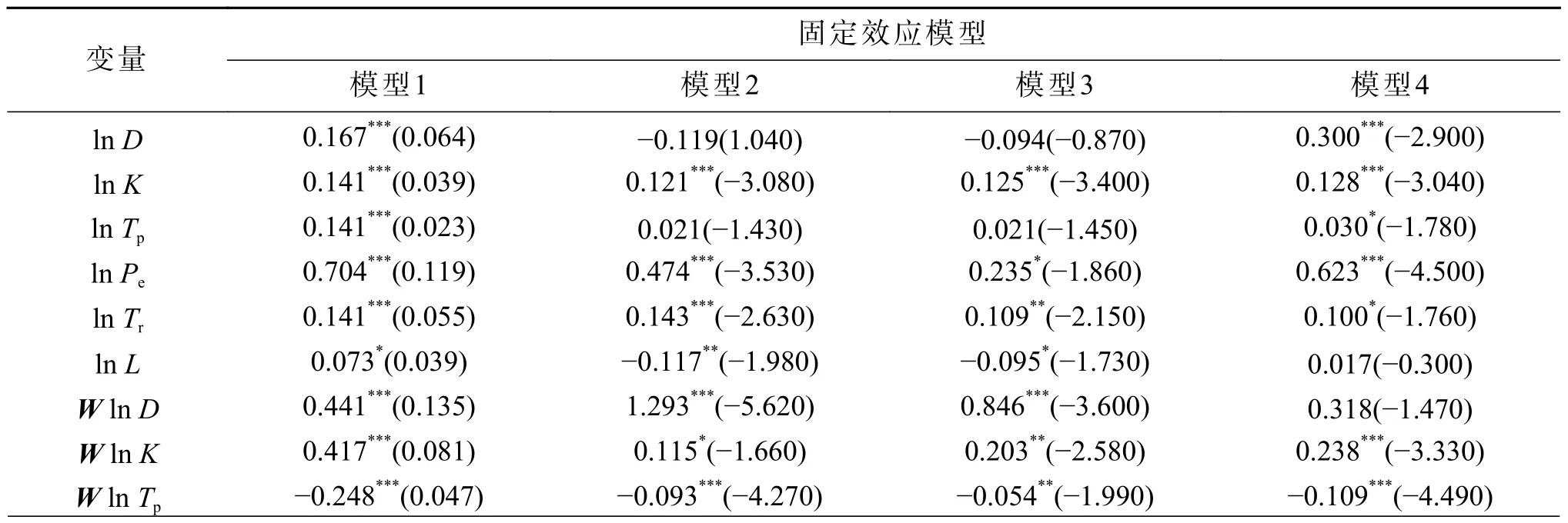
表10 空间杜宾模型实证结果Tab.10 Empirical results of spatial Dubin model

表11 空间面板杜宾模型系数的空间溢出效应分解Tab.11 Spatial spillover effect decomposition of coefficients of spatial panel Dubin model
表11 结果显示,长三角港城协调水平明显与城市经济增长呈正向空间相关性。在空间面板杜宾模型的直接效应中,港城协调度的回归系数为0.139,在5%的置信水平上显著,说明长三角港城协调度每提升1%,城市的人均GDP 就会提高0.139%,随着港城协调水平的提高,城市经济发展水平会随之提高;在间接效应中,港城协调度的回归系数为0.338,1%的置信水平上显著,可见一个城市港城协调水平的提高对周边城市的经济增长具有较强的辐射作用和空间溢出效应。由此可验证本文理论假设,即在控制其他变量的前提下,长三角港城协调发展对城市经济增长具有空间溢出效应。
控制变量中,资本存量、人口结构、交通密度的直接效应和间接效应系数均为正,这是因为城市的资本、人力、交通等方面的支持会使城市经济和产业进入快速发展阶段,提升城市集聚产业、集聚资源、集聚人口的功能[23];科技投入、劳动力资源指标的直接效应显示与城市经济存在正向关系,但间接效应均显示为负。这是因为科技进步和充足的人口密度能为城市经济的发展提供重要保障,但在科技创新投入给创新主体带来巨大利益的同时,会对周围地区带来直接的、显性的负面影响,如环境污染、消耗稀缺资源等问题[24];且科技投入又具有一定的滞后性,地区间存在的一系列组织壁垒和制度壁垒导致科技创新的承接转移存在一定的滞后效应[25]。此外,城市发展过程中会存在城市虹吸效应[26],使得周边地区的劳动力等资源向中心城市靠拢,造成周边城市劳动力资源流失。但间接效应的回归结果显示其未通过显著性检验,这是因为城市虹吸多发生在拥有经济、政治或区位优势的核心城市、中心城市和省会城市,在本研究的港口城市占比较轻,效果不明显。
4 结论与建议
选用2011—2020 年长三角地区33 个地级市的面板数据,运用耦合协调模型对港城协调水平进行测度,通过构建空间杜宾模型探究长三角港城协调水平对城市经济增长影响的空间效应,结果表明:长三角地区港城协调水平整体不高,低度协调港城数量较多,但协调水平迅速发展,动态协调水平逐年优化,具有巨大的潜力和提升空间;长三角地区港城协调水平与城市经济增长均存在较强的空间相关性和空间聚集趋势;长三角地区港城协调水平对城市经济增长的影响存在显著的空间溢出效应,且间接效应大于直接效应,港城协调水平不仅对其所在城市的经济具有显著的促进作用,同时能够带动周边城市经济增长,从而推动区域经济发展。根据以上结论,为进一步提高长三角港城协调水平和促进区域经济一体化发展,提出以下建议:
1) 统筹布局港城建设,提高港城协调水平。港口建设要注意与城市经济规模相匹配,在此基础上进一步完善港口基础设施,扩大港口运营规模,减少同质化现象,拓展新型港口功能;港口城市要根据自身资源禀赋探索构建与现代港口经济配套的先进产业体系,建立配合临港产业的设施;鼓励开展航运金融、航运保险和航运信息等高端服务业,提升产业附加值,增强城市外向能力,充分打造港口城市经济增长新引擎。
2) 加强区域联动分工,联合统筹港城协调。成立三省一市联合群体协同委员会,加强流域资源整合与要素共享,建设区域联动示范区;规划建设跨省域区域投资与联合贸易区,减少行政壁垒,打破地方保护主义,加强区域联动分工;破除体制和技术障碍,增强区域一体化程度,发挥不同地区产业固有优势,实现长三角港城由内部竞争向外部竞争的转变。
3) 发挥空间溢出效应,促进区域经济增长。一方面,可通过高协调港城与低协调港城之间的功能互补,明确功能定位,实现错位发展;另一方面,可构建以高协调港城为中心的区域联运新机制,将高协调港城作为节点构建新航运网络,促进长江黄金水道与东南沿海外向港口的互联互通,带动中、低协调城市经济增长;同时鼓励先进港口进行知识外溢,实现先进管理经验共享,并形成行业标准和规范,带动区域整体进步。

