基于双重控制策略的故障检测方法

刘晓强 ，李 飞 ，李雨婷

(安徽工业大学 a.电气与信息工程学院；b.安徽省智能破拆装备工程实验室；c.安徽省特种重载机器人重点实验室，安徽 马鞍山 243032)

随着社会的不断发展和进步，现代工业生产过程的规模越来越大、复杂程度越来越高，工业过程的运行状态不断向智能化、自动化、集成化等方向发展[1]。现代工业过程各环节相互关联，任一环节出现故障会导致生产过程中部分功能出现故障，甚至导致整个生产过程瘫痪。对于化工生产、高炉炼铁、火力发电和高精密加工等工业过程，若不能及时对过程进行故障检测与识别会造成重大事故[2]。因此，对复杂工业过程进行有效的故障检测是保障工业过程安全生产的有效手段，也是当前过程控制领域的研究热点。

过去几十年，多变量过程监控方法广泛用于故障检测并在工业过程监控中取得巨大成功，如主成分分析(principal component analysis，PCA) 方法[3-7]、独立成分分析(independent component analysis，ICA)方法[8-9]、核主成分分析(Kernel principal component analysis，KPCA)方法[10]、基于核独立成分分析(Kernel independent component analysis，KICA) 方 法[11]等。上述方法可看作是与霍特林T2统计量(简称T2统计量)相结合的数据处理办法，适用于变量间有强相关的数据，不能反映所有变量的故障信息，若原始数据的相关性不强则达不到很好的降维效果，需与其他方法或统计量结合来监控工业过程。为此，研究使用控制图的多变量过程监控方法用于工业过程。Crosier[12]提出一种多元累积控制图法用于检测正态分布变量均值的变化，Runger 等[13]提出一种累积和控制图的多元扩展方法，Liu 等[14]提出一种基于改进欧氏距离控制(improved Euclidean distance control，IEDC)的多变量过程故障检测方法。此类方法是基于控制图的观点并加以改进而提出的，中心性参数值依赖于基础均值向量和协方差矩阵，过程失控时易出现均值向量偏移延迟的现象，致使故障检测效果不佳。为探寻一种能反映过程更多变化信息的多元统计量，并对复杂工业过程进行直接监控，提出一种基于双重控制策略(dual control strategy，DCS)的故障检测方法，统计过程中所有监控变量的故障信息，以期达到良好的故障检测效果。

1 偏差变量与统计量的生成

在复杂的工业过程中，控制变量特性会随机变化进而导致表征信息的数据发生改变，从中可得到所需要的控制信息。为此，对采集的工业过程数据进行预处理，利用偏差变量的计算方法将其生成新的辅助监控统计量，得到参量正常与不正常数据之比，据此调节统计量阈值。

1.1 数据的预处理

数据包含大量信息且各数据的数量级相差很大，无法直接进行计算，需对其进行标准化处理，以保证各样本数据的维度处于同一水平。假设整个工业过程中的多元变量X=(x1,x2,...,xT) ， 其中xi∈R(N×1)(i=1,2,...,T)，T表示观测变量的个数，N表示观测数据的数量。变量相互独立且服从高斯分布xi∼ψ(ui,σ2i)，ui为均值， σ2i为方差。标准差标准化法的定义为

其中x′i为标准化后的数据。

1.2 偏差变量的计算

1.3 统计量的生成

2 基于双重控制策略的多变量过程监控

给定变量的上下限从而确定偏差变量的表达式，实现第一重控制；对偏差变量进行绝对值处理并通过累计求和的方法得到新的辅助监控统计量，实现第二重控制；针对辅助监控统计量阈值不易确定的现象，提出一种基于反馈调节的参数自适应方法设置统计量的阈值。

2.1 变量上下限的选取

其中： µ1， µ2为大于零的系数；Exi，Sxi分别为xi的均值和标准差。若xi的控制区间关于均值对称，则有µ1= µ2；若xi的控制区间不服从均值对称，则系数可由置信区间的原理来确定。当变量服从正态分布时，可根据 3δ原则判断上下限参数的大小，根据置信区间的原理，变量落在 3δ范围内的概率高达99.74%，可信度高，因此可确定系数 µ1和 µ2的值为3。

2.2 统计量阈值的计算

Q的阈值限由置信区间原理确定，表示如下：

其中：Qup，Qdown分别为Q的 阈值上下限；EQ，SQ分别为Q的均值和标准差； η为大于零的系数，由置信区间的原理确定，与上述确定系数 µ1和 µ2的方法相同，设置 η为3。对辅助监控统计量Qa进行分析，该统计量不满足高斯分布，阈值表示如下：

式中：Qa-up，Qa-down分别为统计量阈值的上下限；EQa，SQa分别为Qa的均值和标准差； ρ为大于零的系数。为分析变量上下限对Qa的影响，设置一个新的参量K，为Qa正常数据与不正常数据之比(ratio of normal and fault data，RNFD)。将在Qa阈值限内的数据个数统计到Qa-n中，在阈值限外的数据个数统计到Qa-f中。参量Qa的阈值范围与正常数据和错误数据的个数由参数 ρ确定。一般情况下，正常数据比错误数据多才能使过程数据具有可靠性，即K≥1。从置信区间的原理可知，如果K值太大，会导致多数数据落点在 3δ原则外，不具说服性，在这种情况下需适当降低K值。为保证过程数据的合理性，提出一种基于反馈调节的参数自适应方法稳定K在1～3 之间，设置初始系数 ρ=1。

2.3 故障检测流程

引入偏差变量的概念，并对偏差变量进行绝对值处理，再通过累积求和得到辅助监控统计量Qa。绝对值的存在不会出现均值抵消的情况，同时在统计量控制图中体现出来的效果落差较大，更易观察。使用Qa对工业过程进行故障检测，其流程如图1，具体步骤如下：

图1 基于双重控制策略的多变量过程监控方法流程图Fig.1 Flow chart of multivariate process monitoring method based on dual control strategy

1) 导入训练与测试数据，计算训练数据的均值和方差并进行标准化处理；

2) 确定变量的上下限，并通过计算得到偏差变量；

3) 使用基于双重控制的方法获得Qa，先通过步骤2)得到偏差变量实现第一重控制，再通过对偏差变量进行绝对值处理并通过累计求和得到所需的Qa，实现第二重控制；

4) 确定初始系数 ρ并通过参数自适应策略将参量K稳定在1～3 的范围内；

5) 确定Qa的阈值限；

6) 计算Qa数据的故障检测率和误报率；

7) 比较Qa与设置阈值限的大小得出是否发生故障的结论。

3 TE 过程的实验及结果分析

3.1 仿真实验

依据实际化工反应过程，美国Eastman 公司开发化工模型模拟仿真平台[15]，即田纳西伊斯曼过程(TE 过程)。此平台是一个开放的、具有挑战性的化工过程实验平台，平台产生的数据具有时变、非线性和强耦合的特征，能较好地模拟实际复杂工业过程系统的典型特征[16-17]。产物冷凝器、反应器、产物汽提塔、循环压缩机和汽液分离器是TE 过程的5 个主要操作单元[18]，所有反应都伴随热量的释放，因此反应器中额外的热量由水冷系统进行传递。TE 过程的工艺流程图如图2。

图2 TE 过程工艺流程图Fig.2 TE process flow chart

TE 过程共可收集52 个测量值，包括41 个过程测量变量和11 个过程操纵变量，分为6 种故障类型，共计21 个故障。其中：故障1～7 的主要特征为过程变量的阶跃变化；故障8～12 由过程变量的随机变化引起[19]；故障13 由反应动力学的缓慢变化引起；故障14，15 由阀门黏滞导致；故障16～20 的故障类型未知；故障21 由进料通道4 的阀门固定在恒定位置引起[20]。TE 过程的数据集分为训练集和测试集，训练集数据用于完成标准化处理等工作，总数为500；每个测试集包含960 个样本。为验证文中所提双重控制策略(DCS)故障检测方法的监控性能，采用DCS、改进欧氏距离控制(IEDC) 和主成分分析(PCA) T2和SPE 统计量方法用于TE 过程的故障检测，并进行比较分析。

3.2 仿真结果分析

TE 过程每个测试集包含960 个样本，所有故障从第161 个样本引入直至结束，统计量超过阈值会触发警报。提取TE 过程中具有阶跃故障特征的故障4 与随机变化特征的故障12 进行分析， DCS 方法、IEDC 与PCA 方法对统计量的检测结果如图3～4。图中虚线为阈值线。

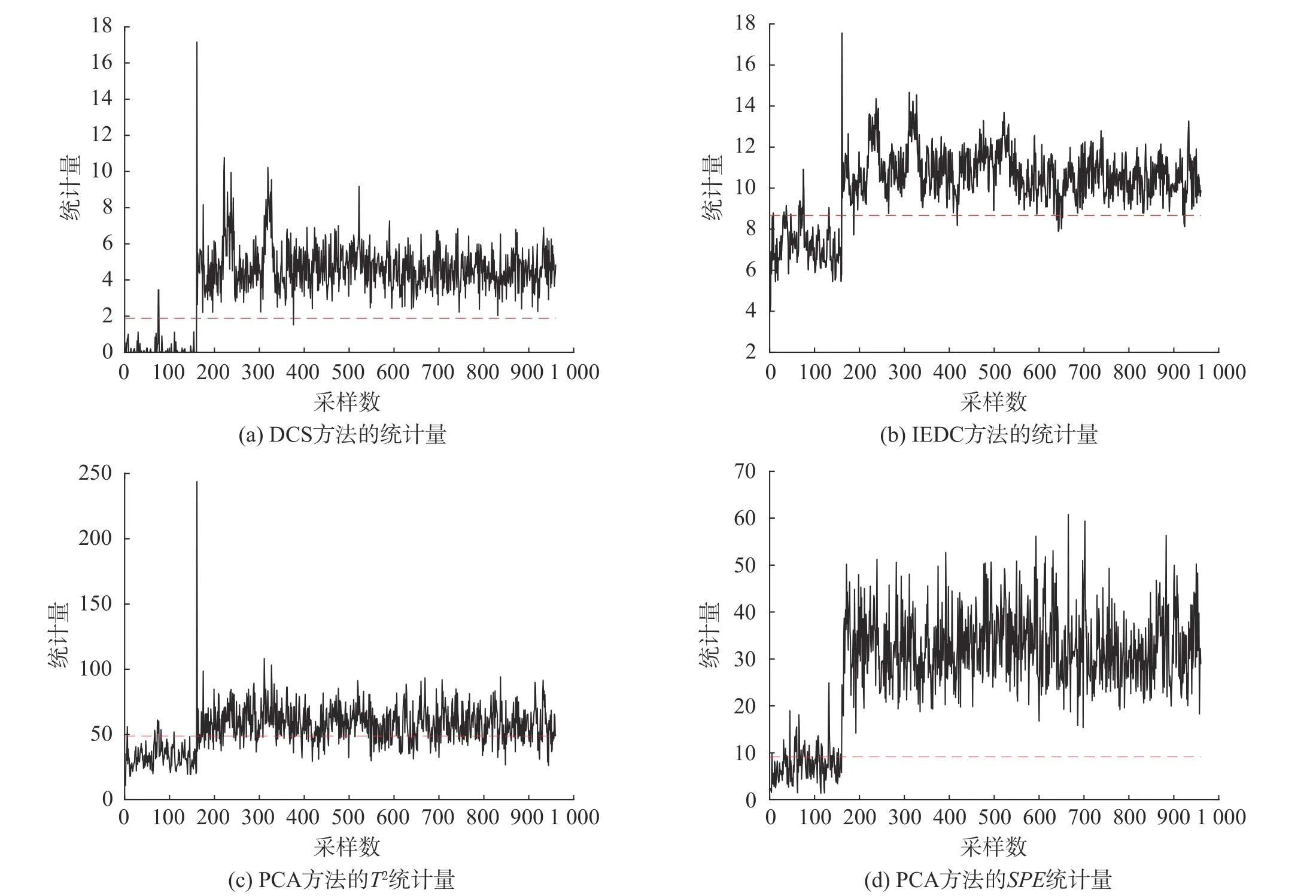
图3 故障4 不同检测方法统计量的检测结果Fig.3 Detection results of different detection methods statistics for fault 4

由图3 可看出：对于故障4，DCS 方法中的Qa可较好地反映内部变量的振动，故障发生时能及时保存故障信息并检测出故障；与IEDC 方法相比，DCS方法在整个测试样本中表现较好；与传统PCA 方法中T2统计量检测相比，DCS 方法在故障发生或不发生时检测效果较好；与SPE 统计量检测结果相比，DCS 方法在故障未发生时检测优势更显著。

由图4 可看出：对于故障12，DCS 方法在故障产生区间里的检测效果比PCA 和IEDC 方法统计量略差，主要是因为随机变化特征导致数据产生波动，对偏差变量的生成产生影响，使其不能完整地收集故障信息；但对于未发生故障的样本范围，DCS方法的检测效果比其他2 种方法更具优势。

图4 故障12 不同检测方法统计量的检测结果Fig.4 Detection results of different detection methods statistics for fault 12

对于工业过程的故障检测，检测指标一般为产品误报率(false alarm rate，FAR)与故障检测率(false detection rate，FDR)。产品误报率指未发生故障时报警的概率，在TE 化工过程为在前160 个采样数据中统计量超过阈值限的概率；故障检测率指发生故障时报警的概率，在TE 化工过程表现为采样数在161～960 中统计量超过阈值限的概率。对TE 化工过程的21 个故障进行检测，分别计算DCS 方法、IEDC 和PCA 方法的故障检测率与误报率，结果如表1。考虑到PCA 方法一般使用T2统计量作为工业过程的检测统计量，表中将DCS 方法数据故障检测率和误报率优于IEDC 方法与PCA 方法的T2统计量检测的数据标黑加粗处理。

表1 不同检测方法的故障检测率与产品误报率Tab.1 Fault detection rate and false alarm rate of different detection methods

由表1 可看出：对于故障3、故障9、故障15、故障19，DCS 方法检测时表现不敏感，故障检测率与产品误报率的效果均不理想，但与IEDC 和PCA方法相比，DCS 方法能反映过程中更多的变化信息，在故障检测率与产品误报率具有优势。原因在于TE 过程变量的相关性是非线性的，且变量中存在噪声，非线性偏差变量的均值和标准差不能仅通过累积求和相互抵消，导致故障检测效果不显著。对于具有阶跃变化特征的故障7，DCS，IEDC，PCA 方法的T2和SPE 统计量的故障检测率均为100%；产品误报率分别为0，4.4%，3.1%和16.3%，DCS 方法在面对阶跃变化特性的故障时能发掘更多的数据信息，对产品误报率检测更敏感。对于黏性变化特征的故障14，DCS 方法、IEDC 方法、PCA 方法的T2和SPE统计量的故障检测率分别为100%，100%，100%和99.6%；产品误报率分别为0，3.1%，9.4% 和21.9%，DCS 方法对产品误报率检测更敏感。对于具有黏性变化特征的故障， DCS 方法先将信息统计到偏差变量再通过累计求和传递给Qa，可减小黏性变化带来的影响并保存更多的数据信息，达到良好的故障检测效果。

4 结论

针对工业过程故障检测效果不佳的问题，提出一种基于双重控制策略的多变量过程监控方法。从变量本身出发提取偏差变量，对偏差变量进行绝对值处理并通过累积求和将得到的故障信息统计到辅助监控统计量；使用基于反馈调节的参数自适应策略确定辅助监控统计量的阈值。将提出的故障检测方法用于TE 过程的仿真分析，并与IEDC 和PCA方法的检测结果进行比较，结果表明所提方法着重统计过程中的多个故障信息，可达到良好的故障检测效果。但变量存在的噪声及工业过程存在的延迟会导致产生更复杂的故障检测问题，下一步研究需考虑这些因素对故障检测的影响。