基于BP-ANN与RBF-ANN的钢筋与混凝土黏结强度预测模型研究

李 涛,刘 喜,李振军,赵小琴

(1.西安交通工程学院 土木工程学院,陕西 西安 710300;2.长安大学 建筑工程学院,陕西 西安 710061;3.西南油气分公司采气二厂,四川 阆中 637400)

钢筋与混凝土能够共同工作的条件是二者间具有良好的黏结,黏结应力为二者间的共同工作提供了保证,当黏结应力过低或丧失时,钢筋与混凝土发生分离,进而影响钢筋混凝土结构的工作性能[1]。因此,钢筋与混凝土的黏结性能在钢筋混凝土结构的裂缝控制中起着至关重要的作用。

考虑到钢筋与混凝土间的黏结强度对于混凝土结构的研究与实际工程应用均有着重要的意义。为此,国内外学者开展了大量的试验研究与理论分析,提出了黏结强度的经验或半经验公式、纯理论计算模型。基于中心拉拔试验,徐有邻[1]、Gao等[2]和相关规范[3]分析了黏结强度的5个主要影响因素,对此提出了黏结强度经验计算式。基于黏结破坏机制,Tepfers[4]分析了内裂缝发展的全过程,提出了内裂缝不同发展阶段所对应的黏结强度理论模型。目前,预测钢筋与混凝土黏结强度的理论模型与经验公式主要考虑混凝土强度、保护层厚度、钢筋直径、锚固长度及配箍率等重要影响因素,基于试验数据进行回归分析得到黏结强度的计算式显然无法表达各因素间的复杂非线性关系,而诸多研究均表明人工神经网络方法具有强大的非线性映射能力[5-6]。

人工神经网络(ANN)具有强大的非线性拟合能力、自主学习能力等优点,已被广泛应用于强度预测[7]、评标环节[8]、老年驾驶员事故的性别特征预测[9]等领域。王毅红等[7]利用人工神经网络方法对生土砖的抗压强度进行预测,表明神经网络方法预测精度优于回归分析方法。瞿王健等[10]认为,反向传播(BP)神经网络优化方法能很好地防止污闪事故的发生。宋早雪等[8]研究发现,运用ANN科学地评价多因素下的投标方案,便于招标商快速选择最佳单位。

收集290组钢筋与混凝土间黏结性能试验数据,以归一化和标准化处理的混凝土强度、保护层厚度、钢筋直径、锚固长度和配箍率为输入参数,建立了基于反向传播人工神经网络(BP-ANN)和径向基函数神经网络(RBF-ANN)的黏结强度预测模型,对比分析预测模型与现有经典模型(徐有邻模型、Tepfers模型)预测值的精度和离散性,验证预测模型的可行性与有效性,以实现ANN对黏结强度的合理预测。

1 黏结强度模型

1.1 BP-ANN预测模型

1.1.1 BP-ANN模型建立

BP-ANN是基于数据集,在输入变量与输出变量间建立一定关联的神经网络方法[9]。BP-ANN有着推导过程严谨、通用性广、物理概念清楚等优势。3层(输入层、输出层、隐含层)的神经网络即可映射任意非线性关系[9],因此本文通过MATLAB软件[11-12]建立3层BP-ANN,网络训练选用神经元内部的sigmoid函数(式(1)和(2))[13],能获得最优拟合效果,其训练过程见图1。考虑到增加隐含层节点数目可获得较低的误差,其训练效果易实现。因此,为测试不同隐含层神经元数目对人工神经网络模型性能的影响,依次建立隐含层神经元数目为5、10、15、20、25、30的3层BP-ANN,对黏结强度数据进行拟合。为提高样本集的利用率,将数据库随机分成3个数据集,即70%训练数据集、15%验证数据集、15%测试数据集。

神经元之间的信息主要由权值与阈值调整。在训练过程中,根据误差函数的赋值来调整权值与阈值,更新后的权值与阈值分别由式(3)和(4)表示[7,9]。

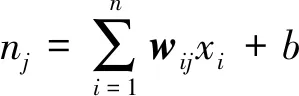
(1)

yj=F(nj)=(1+e-nj)-1

(2)

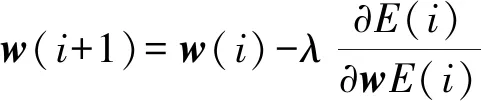
(3)

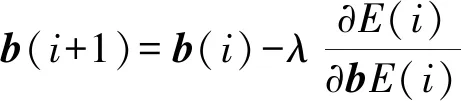
(4)

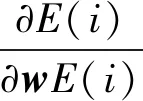
1.1.2 参数选取与处理

笔者收集了290组钢筋与混凝土间的黏结性能试验数据,选取混凝土强度、保护层厚度、钢筋直径、锚固长度以及配箍率作为影响黏结性能的主要因素,样本集详见表1。由于部分文献的混凝土轴心抗拉强度缺失,采用《混凝土结构设计新规范》[3]计算公式,由混凝土立方体抗压强度进行折算得到。虽然钢筋与混凝土间的黏结强度主要考虑的是混凝土抗拉强度,但考虑到混凝土抗拉强度具有较大离散性,故本文提出的神经网络方法将混凝土抗压强度亦作为影响因素进行考虑。

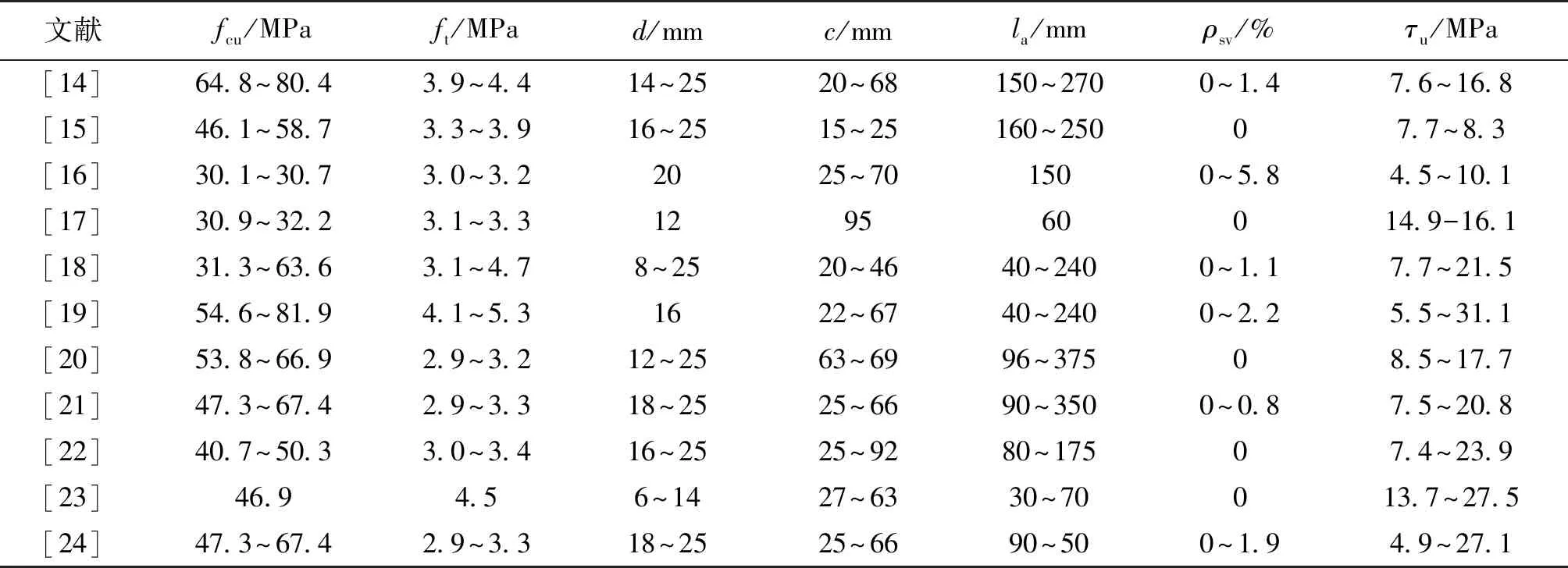
表1 黏结-滑移试验数据汇总

为提高BP-ANN的训练效率,将样本集进行预处理,使黏结强度的预测结果更具有精确性。为避免输入或输出向量中数值大的绝对误差大、反之误差小,部分学者[5,7,25]对输入和输出向量进行归一化处理,但归一化处理依赖于所有的样本集,当有新样本加入时,会影响最大值与最小值。而标准化处理只依赖于当前的数据,并且目前将标准化作为预处理方法的研究很少。因此,为比较两种预处理方法对预测结果的影响,本文采用归一化和标准化两种方法对样本集进行预处理。

在对黏结强度进行神经网络预测后,再根据式(5)和(6)反演计算,得到黏结强度实际预测值。

归一化计算公式为

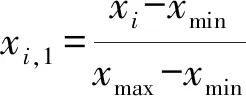
(5)

标准化计算公式为

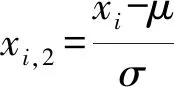
(6)

式中:xi为原始样本集;xmin和xmax分别为样本集的最小值与最大值;μ和σ分别为平均值与标准差;xi,1和xi,2分别为归一化和标准化以后得到的数值。

1.1.3 BP-ANN的检验

为防止训练、测试和验证模型在学习过程中出现局部优化的现象,在训练开始前,应当把黏结强度数据的顺序打乱,排除原始数据的规律性。按照上述BP-ANN训练过程,采用归一化和标准化两种预处理方法得到的数据对黏结强度进行训练,其预测结果详见表2。为了更直观地比较两种预处理方法对黏结强度预测结果的影响,本文选取平均值(μ)、标准差(σ)、变异系数(δ)作为评价指标。

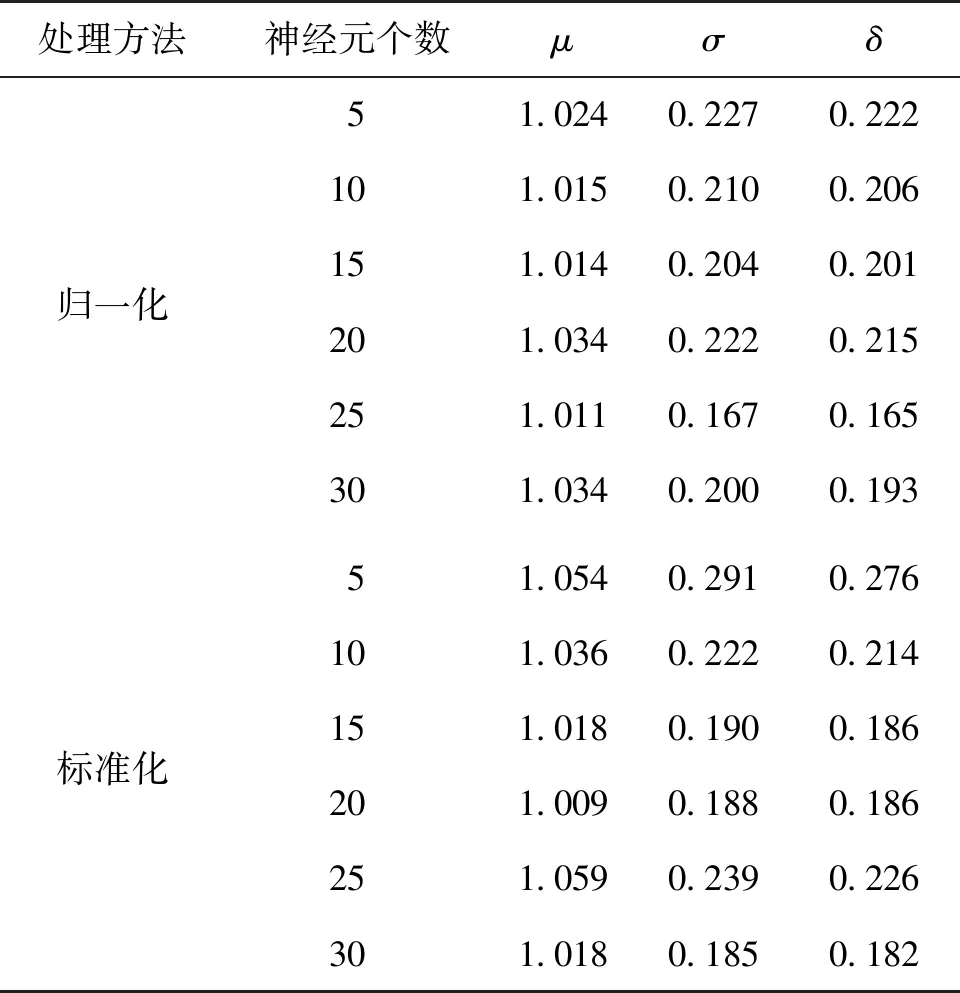
表2 基于BP-ANN的黏结强度预测结果

由表2可知:采用归一化和标准化两种方式进行数据预处理时,利用前一种方法得到的平均值略小于后者,表明数据更为集中,更能提高精度。但当采用min-max的归一化方法处理数据时,当有新数据加入,可能会导致min和max的数值发生变化,需要多次重新定义。

选取归一化和标准化各自对应的最优神经元个数(25和20),绘制黏结强度预测值(τcal)与实测值(τtest)的关系(图2)。由图2可发现:基于BP-ANN的黏结强度模型训练集的数据点都均匀分布在x=y(图中的虚线)的两侧,且拟合结果均接近虚线,表明BP-ANN模型的预测值与实际值的偏差较小,且神经元个数为25(归一化处理)和20(标准化处理)的模型训练效果均表现良好。由表2还可看出:相比之下,经过标准化处理的BP-ANN模型(神经元个数为20)的黏结强度平均值(1.009)更接近1,表明标准化最优神经元个数少,精度更高,且数据预处理更符合实际分布。

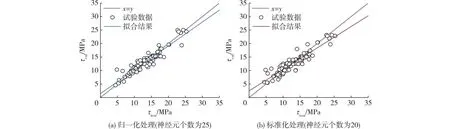
图2 BP-ANN的黏结强度预测值与实测值的关系Fig.2 Relationship between predicted and actual values of bond strength in BP-ANN

1.2 RBF-ANN预测模型

1.2.1 RBF-ANN模型建立

RBF-ANN同样也是由输入层、隐含层、输出层组成,具有强大的非线性映射能力[6]。与BP-ANN不同的是,其收敛速度快、隐含层神经元数目在训练过程中能够自适应调整,最终可获得连续函数的最优预测结果。RBF-ANN基本结构见图3。

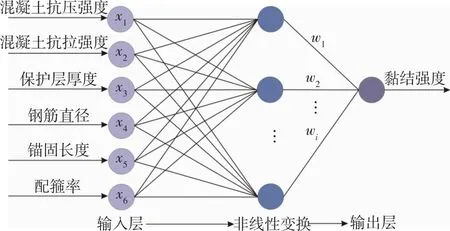
wi为第i个隐含层到输出层的权值图3 RBF-ANN的基本结构Fig.3 Basic structure of RBF-ANN

采用RBF-ANN预测钢筋与混凝土的黏结强度时,使用MATLAB软件自带的径向基函数,只要调用函数,使用sim仿真函数即可获得预测值。考虑到影响模型性能的参数主要是扩展常数Spread的取值,通过对Spread不断地进行试算,发现当Spread为0.085时,预测结果最优。网络训练具体流程为

1)选择数据。分析变量间的相关性,将选取的6个变量作为RBF-ANN预测黏结强度的输入,输出为黏结强度。

2)数据预处理。为提高网络的训练精度和速率,在输入样本前,对样本集进行预处理。

3)初始化。确定好RBF-ANN输入层的变量数目与隐含层的神经元数目。

4)开始训练。将选取的6个变量数据输入到网络中训练,产生6维向量,让6维向量与阈值相乘,再通过径向基函数传递,获得黏结强度预测值与试验值的误差,通过不断地进行调整与修正,达到设定的误差范围为止。

5)测试RBF-ANN。将290组试验值输入到训练好的预测模型中,对比分析输出的结果与实测值。

1.2.2 RBF-ANN的检验

与BP-ANN训练方式类似,同样在训练前将样本数据集顺序打乱,对数据进行预处理。采用两种预处理方法得到的平均值均为1.016、标准差均为0.161、变异系数均为0.158,说明两种预处理方法任选取一种用于RBF-ANN中均是可行的,均能很好地提高预测精度。

由上述可知两种预处理方法获得的评价指标一样,因此选取标准化方法下的预测值与实测值来表征黏结强度预测值与实测值的关系(图4)。由图4可知:基于RBF-ANN的黏结强度模型训练集的数据点都均匀分布在x=y(图中虚线)的两侧,且拟合结果均接近虚线,数据点只有少数偏离虚线,表明数据离散程度较小、波动不明显,更加接近实测值,进而说明RBF-ANN模型的预测值与实测值偏差较小,模型训练效果良好。

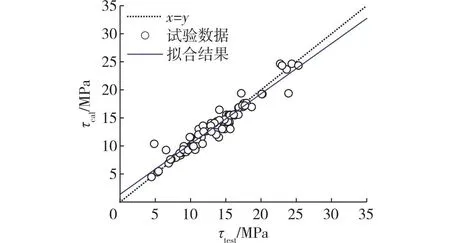
图4 RBF-ANN的黏结强度预测值与实测值的关系Fig.4 Relationship between predicted and actual values of bond strength in RBF-ANN

1.3 模型对比

利用3种评价指标对预测模型与徐有邻模型[1]、Tepfers模型[4]进行对比(表3)。由表3可知:采用标准化处理的BP-ANN(隐含层神经元个数为20的3层神经网络)与RBF-ANN预测的黏结强度预测值与实测值比值的平均值(1.009和1.016)更接近1、标准差(0.188和0.161)更接近0。结果表明:预测模型的预测值与实测值相对接近,且离散性较小。

表3 计算模型对比结果

图5给出了各模型的预测结果与实际测量结果的分布。由图5可知:与现有典型模型相比,BP-ANN与RBF-ANN的黏结强度预测值与实测值吻合良好,预测模型精度较高、离散性较小,结果表明,神经网络能有效筛选出了对黏结强度影响显著的关键因素,进一步说明神经网络方法的泛化能力更强。相比之下,徐有邻模型[1]表现出较大的离散性和偏差,而Tepfers模型[4]的预测结果相对保守一些。

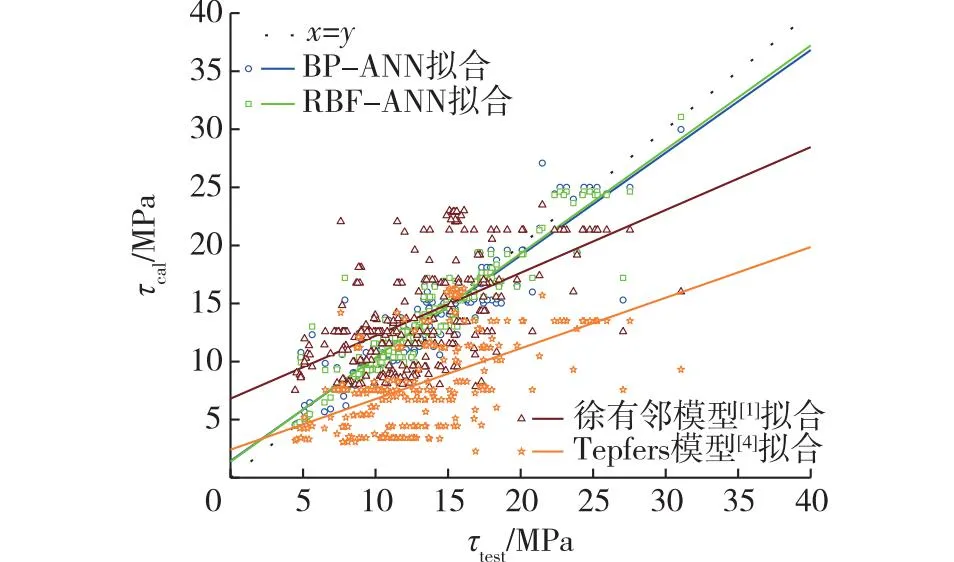
图5 神经网络与现有典型模型的对比Fig.5 Comparison between neural network with the existing typical models

2 临界锚固长度

钢筋锚固长度的确定对混凝土结构的应用和推广具有重要意义,而锚固长度建议值的取定需基于临界锚固长度进行可靠度分析。将钢筋达到屈服条件时但未发生锚固破坏的锚固长度作为钢筋的临界锚固长度,其计算式为

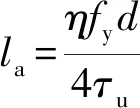
(7)

式中:la为钢筋的临界锚固长度;fy、η和d分别为钢筋的屈服强度、应力丰度系数和直径。

《混凝土结构设计新规范》[3]中给定了钢筋的基本锚固长度,如式(8)所示。

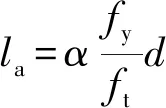
(8)

式中:α为钢筋的外形系数。

基于样本集,得到普通混凝土α的取值范围为0.010～0.140。为保证安全,α取值为0.100,代入式(8)可得出钢筋与普通混凝土的临界锚固长度计算式,如式(9)所示。

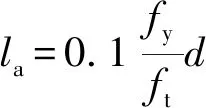
(9)

3 结论

基于收集的黏结锚固试验数据库和黏结强度经典计算式,采用BP-ANN与RBF-ANN两种神经网络方法进行预测,可得到以下结论:

1)与传统回归方法相比,神经网络方法预测结果更为精确,具有较强的泛化能力。

2)基于BP-ANN与RBF-ANN两种神经网络方法预测黏结强度,均具有较高的精度;而RBF-ANN预测的平均值(1.016)大于前者的平均值(1.009),因此BP-ANN预测黏结强度的准确度更高。

3)经过标准化处理的BP-ANN模型(神经元数目为20)的预测精度最高,且数据预处理更符合实际分布;经过归一化和标准化处理的RBF-ANN模型的预测精度基本相同。

4)利用样本集统计分析得出,钢筋与普通混凝土的α取为0.100较为合适,并提出了钢筋与普通混凝土临界锚固长度的计算式。