层状地基土水平抗力比例系数反演的杂交粒子群算法

朱伟鑫,孙前林,吕 乐,王旭东

(1.南京工业大学 岩土工程研究所,江苏 南京 211800;2.中建八局 第三建设有限公司,江苏 南京 210046)

基坑支护结构水平位移是评价基坑设计合理性和基坑工程安全性的重要指标,地基土水平抗力系数的比例系数(m,即水平抗力比例系数)直接影响基坑工程中支护结构的水平位移。由于地基土水平抗力比例系数影响因素众多,合理取用地基土水平抗力比例系数已成为基坑支护结构变形计算的难题。

地基土水平抗力比例系数取值的主要方法有单桩水平荷载试验法[1]、考虑土类和水平位移的规范查表法[2-4]、利用土体强度参数的公式计算法[5]。由于单桩水平荷载试验中单桩与基坑工程中支护桩的受力特性和位移模式不同,由单桩水平荷载试验法确定的m值应用于基坑工程设计时存在局限性;基于经验总结的各类规范查表法,地基土的m值的取值范围宽泛,同一地基土采用不同规范得到的m值存在差异;土体强度参数的公式计算法虽然体现了土性对m值的影响,但计算中涉及基坑底面处支护结构水平位移量的经验值,给m值带来不确定性,易造成基坑工程设计的不安全。

文献[6-8]研究表明,利用支护结构水平位移实测数据的地基土水平抗力比例系数反演分析法,真实反映基坑工程中支护结构与地基土相互作用特性,是合理获取地基土水平抗力比例系数的有效途径。

反演分析的实质是目标函数的极值和参数“最优值”的求解,高效的优化计算方法是反演分析合理求解的关键。单纯形法[6-7]、拟牛顿法[8]、修正Gauss-Newton法[9]等最优化方法在地基土水平抗力比例系数反演分析中得到应用,但这些方法也存在计算稳定性不足和计算收敛慢等局限性[10],尤其是在层状地基的多参数反演中更为突出。

仿生算法[11]为多参数复杂问题的优化求解提供了有效途径,粒子群算法(PSO)[12]模仿了鸟群以最优途径寻找食物的捕食方式,实现了最优化问题的高效求解。粒子群算法与支持向量回归机结合,在深基坑变形预测模型的参数优化[13-15]、地基土弹性模量反演[16]中得到了应用,提高了基坑水平位移的预测精度。为了避免粒子群算法易陷入局部极值,引入遗传算法交叉策略的杂交粒子群算法在含水层导水系数、贮水系数和越流因数的多参数反分析中得到应用[17],验证了杂交粒子群算法求解多参数优化问题的有效性和反演参数的合理性。文献[15-17]研究表明,粒子群算法的原理简单且计算效率高,适用于多参数拟合的最优化问题求解,可为层状地基土水平抗力比例系数反演提供高效的优化计算方法。

为此,基于基坑支护结构水平位移监测数据和支护结构杆系有限元法,以支护结构水平位移离差平方和为目标函数建立地基土水平抗力比例系数反演计算模型,通过引入粒子群优化算法,以实现基坑工程中层状地基土水平抗力比例系数的反分析求解。

1 基坑支护结构计算方法

1.1 基坑支护结构计算模型

现有《建筑基坑支护技术规程》[5]中采用平面杆系弹性支点法作为基坑支护结构计算方法,基坑支护结构计算模型如图1所示,以弹性地基梁理论为基础,基坑支护结构挠曲微分方程可表示为式(1)和(2)。

(1)

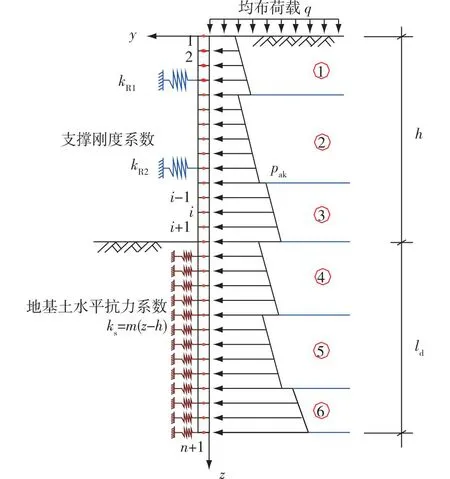
图1 基坑支护结构计算模型Fig.1 Calculation model of supporting structure in excavations

(2)

式中:y为支护结构水平位移,m;z为土层深度,m;EI为支护结构计算宽度范围内的抗弯刚度,kN·m2;m为地基土水平抗力比例系数,kN/m4;h为基坑开挖深度,m;ld为支护结构入土深度,m;pak为主动土压力强度标准值,kN/m2;b0为地基土水平抗力的计算宽度,m;bs为土压力计算宽度,m。

对于墙后土压力模式分布简单且无锚杆/支撑的基坑工程问题,可由式(1)和(2)支护结构挠曲微分方程,结合支护结构顶、底两端边界条件,求得支护结构挠曲微分方程解析解,计算支护结构位移和内力。

1.2 基坑支护结构杆系有限元法

对于层状地基基坑工程,墙后土压力模式分布复杂且设置有锚杆/支撑的基坑工程问题,无法直接求得支护结构微分方程解析解。为了计算复杂工况下基坑支护结构水平位移,需要依据基坑支护结构计算模型和支护结构挠曲微分方程,建立考虑基坑开挖和支撑施工过程的基坑支护结构有限元计算方法,计算支护结构位移和内力。

将图1中支护结构剖分为n个梁单元,在地基土与支护结构的相互作用满足变形协调和静力平衡条件下,考虑基坑开挖和支撑施工过程的支护结构杆系有限元整体平衡方程,见式(3)。

(K+KS+KR)y=P+KRy0

(3)

式中:K为支护结构整体刚度矩阵;KS为墙前地基土整体刚度矩阵;KR为支撑整体刚度矩阵;P为支护结构墙后土压力荷载和预加支撑轴力组成的整体荷载向量;y为支护结构整体水平位移向量;y0为支撑设置前支护结构整体水平位移向量。

K、KS、KR由单元矩阵集成,相应的矩阵系数计算方法参见文献[5,18]。P由单元荷载向量集成,结点荷载的计算方法参见文献[19]。

由于梁单元的结点自由度为2,土单元的结点自由度和支撑的结点自由度皆为1。故K为2(n+1)×2(n+1)阶矩阵,而KS和KR为(n+1)×(n+1)阶矩阵,因此在形成(K+KS+KR)整体刚度矩阵时,需将KS和KR的矩阵阶数扩充一倍,以适应支护结构刚度矩阵的阶数,并将地基刚度和支撑刚度的矩阵系数叠加到支护结构刚度矩阵相应位置。

式(3)可建立与施工工况相适应的基坑支护结构杆系有限元整体平衡方程,在引入支护结构边界条件后,即可求得基坑支护结构的水平位移、转角和内力。

2 水平抗力比例系数的位移反分析法

2.1 位移误差目标函数

地基土水平抗力比例系数反演是一个非线性误差函数最小化的优化问题,通过寻求地基土水平抗力比例系数的最优解,使得有限元正分析得到的支护结构水平位移计算值最大限度地接近支护结构水平位移实测值。位移误差目标函数(ΔY)用支护结构水平位移实测值和计算值的离差平方和表示,见式(4)。

(4)

式中:M为测点个数;yi为第i个测点的水平位移实测值,m;yi(ξ)为第i个测点的水平位移计算值,m;ξ为基坑开挖面以下地基土的水平抗力比例系数(m1,m2,…,mi,…,mk),kN/m4;k为基坑开挖面以下土层数。

当位移误差目标函数取得最小极值时,即得到地基土水平抗力比例系数的最优解。

2.2 水平抗力比例系数约束条件

为了合理、有效地反演地基土水平抗力比例系数,通过对地基土水平抗力比例系数辅以适当约束条件来保证最优解的稳定性与唯一性,水平抗力比例系数的初值选取和约束条件为式(5)。

mi,min≤mi≤mi,maxi=1,2,3,…,k

(5)

式中:mi,min和mi,max为地基土水平抗力比例系数的上限值和下限值,可根据地基土性质和规范给定的地基土水平抗力比例系数的取值范围确定[2-5]。

由式(4)和(5)构建了地基土水平抗力比例系数反分析计算模型,计算模型为多参数非线性规划问题,需要采用最优化方法寻找地基土水平抗力比例系数的最优解。

2.3 粒子群算法

高效的最优化计算方法是反分析的关键,粒子群算法等克服了传统算法的不足,提高了计算效率,为多参数优化反演分析提供了新的有效途径。

对于k层地基土的水平抗力比例系数寻优反演问题,粒子群算法假设在k维空间中有N个粒子Xi={mi1,mi2,mi3,…,mik}(i=1,2,…,N)组成的粒子群,每一粒子即为层状地基土的一组水平抗力比例系数潜在解,通过计算每一粒子的位移误差目标函数值,确定粒子的自身历史最优极值与粒子群其余粒子的历史最优极值,并据此不断动态调整粒子的位置和速度,粒子位置调整意味着地基土水平抗力比例系数的变化,粒子速度调整意味着地基土水平抗力比例系数变化的大小和方向,从而生成新的粒子群体。通过上述寻优机制,在k维空间中不断搜索地基土水平抗力比例系数的最优解,直至寻优计算满足收敛条件。

为了避免粒子群算法陷入局部最优解的问题[20],在粒子群算法的基础上,引入遗传算法中的交叉策略,对粒子进行随机杂交,通过优化粒子位置和速度的调整规则,形成了杂交粒子群算法[21]。

2.4 粒子群算法收敛条件

为了在地基土水平抗力比例系数反演计算中求得最优解,基于粒子群算法的寻优计算采用双控收敛条件,设定地基土水平抗力比例系数和位移误差目标函数前后两次计算值的相对误差均小于1%。地基土水平抗力比例系数反演计算收敛条件可表示为式(6)和式(7)。

(6)

(7)

式中:j为迭代次数。

在满足收敛性的基础上,为了减小反演计算陷入局部极值的可能性,保证最优解的稳定性,寻优计算必须在连续满足收敛条件10次后结束。

2.5 水平抗力比例系数反演计算步骤

地基土水平抗力比例系数反演是利用粒子群算法实现位移误差目标函数最小极限值的寻优计算,具体步骤如下:

1)利用规范[5]给定的水平抗力比例系数经验值范围,结合土性给定地基土水平抗力比例系数的初值,利用支护结构杆系有限元法计算支护结构的水平位移。

2)依据支护结构水平位移计算值和实测值,由式(4)建立位移误差目标函数。

3)利用粒子群算法的寻优机制,逐次调整地基土水平抗力比例系数,使地基土水平抗力比例系数和位移误差目标函数同时满足收敛条件和稳定条件,相应的地基土水平抗力比例系数即为最优解。

3 方法验证和工程应用

3.1 水平抗力比例系数反演的粒子群算法验证

为了验证粒子群算法在地基土水平抗力比例系数反演中的计算效率和参数反演值的准确性,利用如图2所示的基坑工程算例[22],开展地基土水平抗力比例系数的反分析。

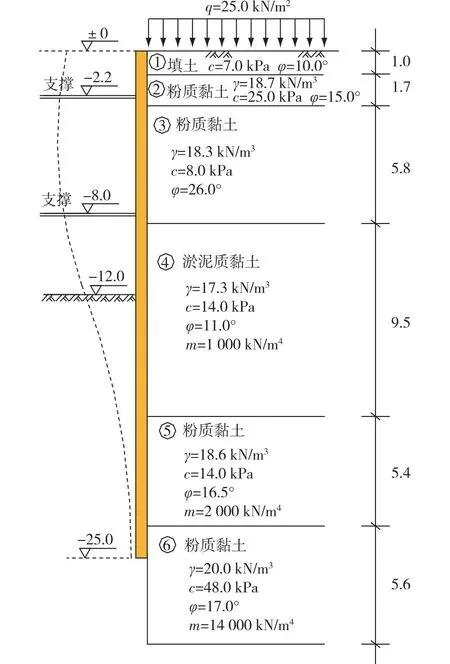
γ—土的重度;c—土的黏聚力;φ—土的内摩擦角图2 地基土分布和基坑支护结构[22](m)Fig.2 Foundation soil distribution and supporting structure in excavations[22](m)

基坑开挖深度为12.0 m,支护结构采用钻孔灌注桩,桩长为25.0 m,桩径1 200 mm,桩间距1 300 mm。在-2.2和-8.0 m处设置两道混凝土支撑,支撑截面分别为800 mm×1 000 mm和800 mm×800 mm,支撑间距分别为8.0 m和16.0 m,支撑长度为61.0 m。钻孔灌注桩和支撑的混凝土等级为C25,地面超载为25 kPa。粒子群算法和杂交粒子群算法的计算参数见表1。

表1 粒子群算法和杂交粒子群算法的计算参数

基坑底面以下的④淤泥质黏土、⑤粉质黏土和⑥粉质黏土的水平抗力比例系数分别取1 000、2 000和14 000 kN/m4。

首先,将支护桩剖分为100个梁单元,建立基坑支护结构杆系有限元整体平衡方程,计算基坑开挖深度12.0 m工况下支护结构的水平位移;其次,将有限元正分析得到的支护结构水平位移作为位移目标函数中的水平位移实测值,建立位移误差目标函数;最后,利用粒子群算法和杂交粒子群算法实现地基土水平抗力比例系数反演计算模型的求解,获得地基土水平抗力比例系数反演值。

图3为层状地基土m和ΔY的收敛过程。由图3可知:m和ΔY均随粒子迭代次数的增加而逐渐收敛,但收敛过程中m呈现一定的起伏变化,ΔY呈现阶梯状减小。

分析收敛过程发现,当m和ΔY满足收敛性时,m并非都收敛于给定的真值,存在阶段性“假稳定”现象。为了防止优化计算出现阶段性“假稳定”进而导致m陷入局部极值,有必要在满足收敛条件基础上进一步观察m反演值的稳定性。根据对本算例中m的收敛过程分析,优化计算连续10次满足收敛条件是保证最优解稳定性的基本条件。

表2为层状地基土的m反演值。由表2可知:满足m稳定条件时,粒子群算法和杂交粒子群算法的迭代次数分别为52次和35次,m反演值的最大相对误差分别为4.75%和1.74%。总体上,2种最优化方法在m的反演分析中都具有较好的适用性,但杂交粒子群算法具有更高的计算效率和计算精度。

3.2 工程应用

文献[6]中的基坑工程开挖深度为10.0 m,采用φ800@1 000的钻孔灌注桩作为挡土结构,桩长为18.0 m,桩顶位于地表下1.5 m处,设置一道600 mm×700 mm钢筋混凝土内支撑。基坑开挖分两阶段施工:基坑开挖至-4.0 m;设置钢筋混凝土支撑并继续开挖到-10.0 m。基坑开挖过程中对支护结构的水平位移进行了现场监测,已测得基坑开挖至-4.0和-10.0 m时支护结构水平位移的监测数据。地基土分布和基坑支护结构见图4。粒子群算法和杂交粒子群算法的计算参数见表1。

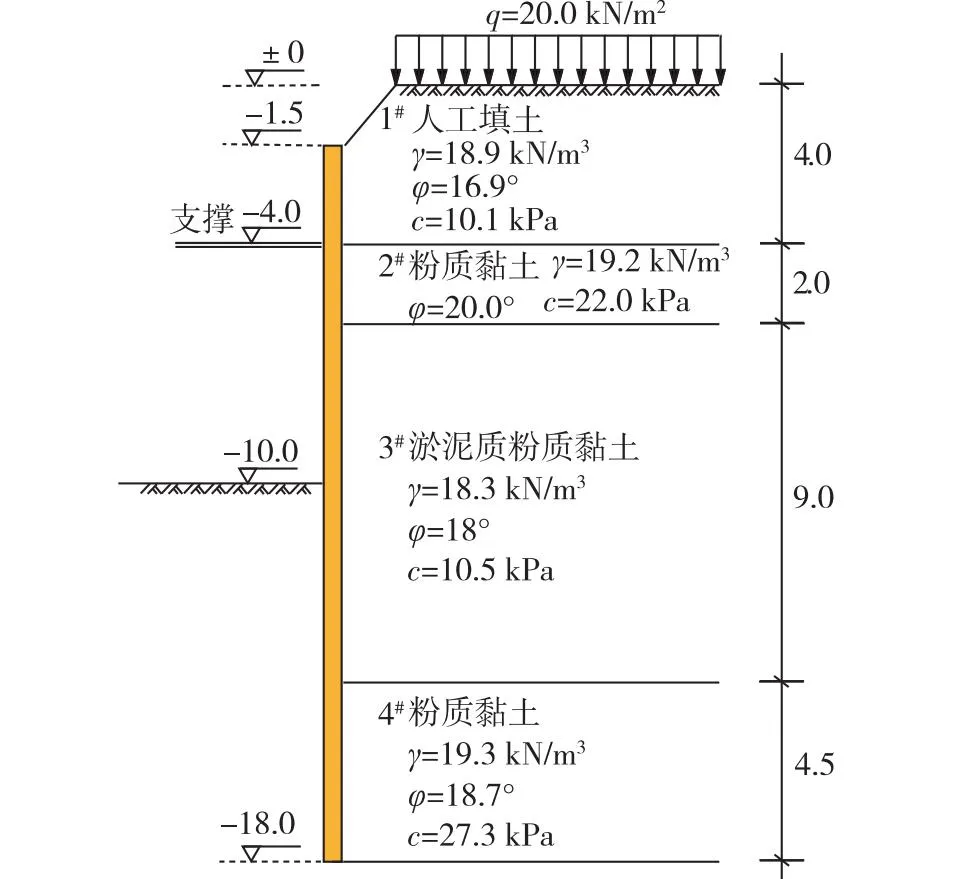
图4 地基土分布和基坑支护结构[6](m)Fig.4 Foundation soil distribution and supporting structure in excavations[6](m)

将支护桩均匀划分为72个梁单元。m初始值均取1 000 kN/m4,然后用支护结构杆系有限元计算支护结构水平位移,结合基坑开挖至-4.0 m时测得的支护桩水平位移建立ΔY,最后用粒子群算法和杂交粒子群算法对基坑底面下m进行反演计算。在此基础上,利用m反演值对基坑开挖至-10.0 m时的支护结构水平位移进行预测,并与水平位移实测值对比,验证水平位移预测结果的合理性。

3.2.1 均匀地基土的m反演值

基坑开挖至-4.0 m时,坑底以下、支护结构范围内有2#粉质黏土、3#淤泥质粉质黏土和4#粉质黏土。为了简化反演计算,可将基坑开挖面以下三层土视为均匀土层,即将反演问题简化为在一维空间中寻找m的最优解。图5为基坑开挖至-4.0 m时均匀地基土的m和ΔY的收敛过程。

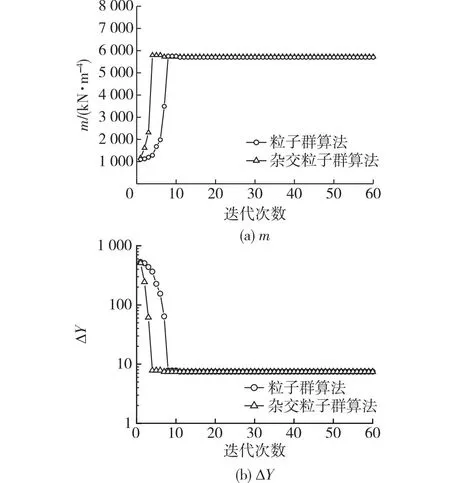
图5 均匀地基土的m和ΔY的收敛过程(基坑开挖至-4.0 m)Fig.5 Convergence process of m and ΔY in uniform foundation soil (excavation to -4.0 m)

由图5可知:2种最优化方法的收敛速度快且稳定。均匀地基土的m反演值见表3。由表3可知,满足收敛要求时杂交粒子群法的迭代次数少,ΔY也小,计算效率更高。以杂交粒子群算法的m反演值为基础,2种优化方法之间m值的差异大约为0.45%,2种方法反演得到的均匀地基土m值均在规范[2-4]参考值的合理取值范围内,说明了m反演值的合理性和工程适用性。

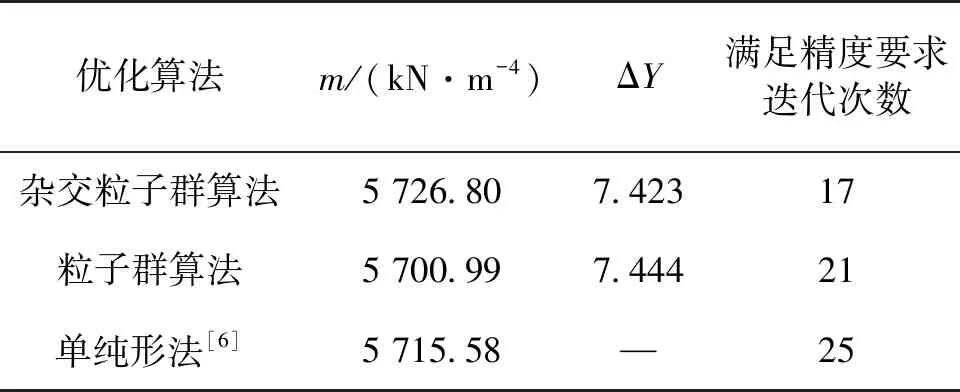
表3 均匀地基土的m反演值

与文献[6]中单纯形法相比,m反演值的一致性良好,从迭代次数的对比可知,粒子群算法和杂交粒子群算法的计算效率高于传统的单纯形法优化算法。

3.2.2 多层地基土的m反演值

m与土的物理力学性质密切相关,将基坑开挖面下土层作为均匀土层反演计算m,虽然简化了计算过程,但在真实反映多层地基土的水平抗力特性上不尽合理。为了更好地反映不同土层的水平抗力特性,充分反映实际土层分布对基坑支护结构工作性状的影响,并与实际土层分布条件下的支护结构水平位移实测值相匹配,有必要建立多层地基土m的反演计算模型,在多维空间中搜寻多层地基土m的组合最优解。基坑开挖至-4.0 m,多层地基土的m和ΔY的收敛过程如图6所示,总体来看,2种最优化方法的收敛速度较快且稳定。

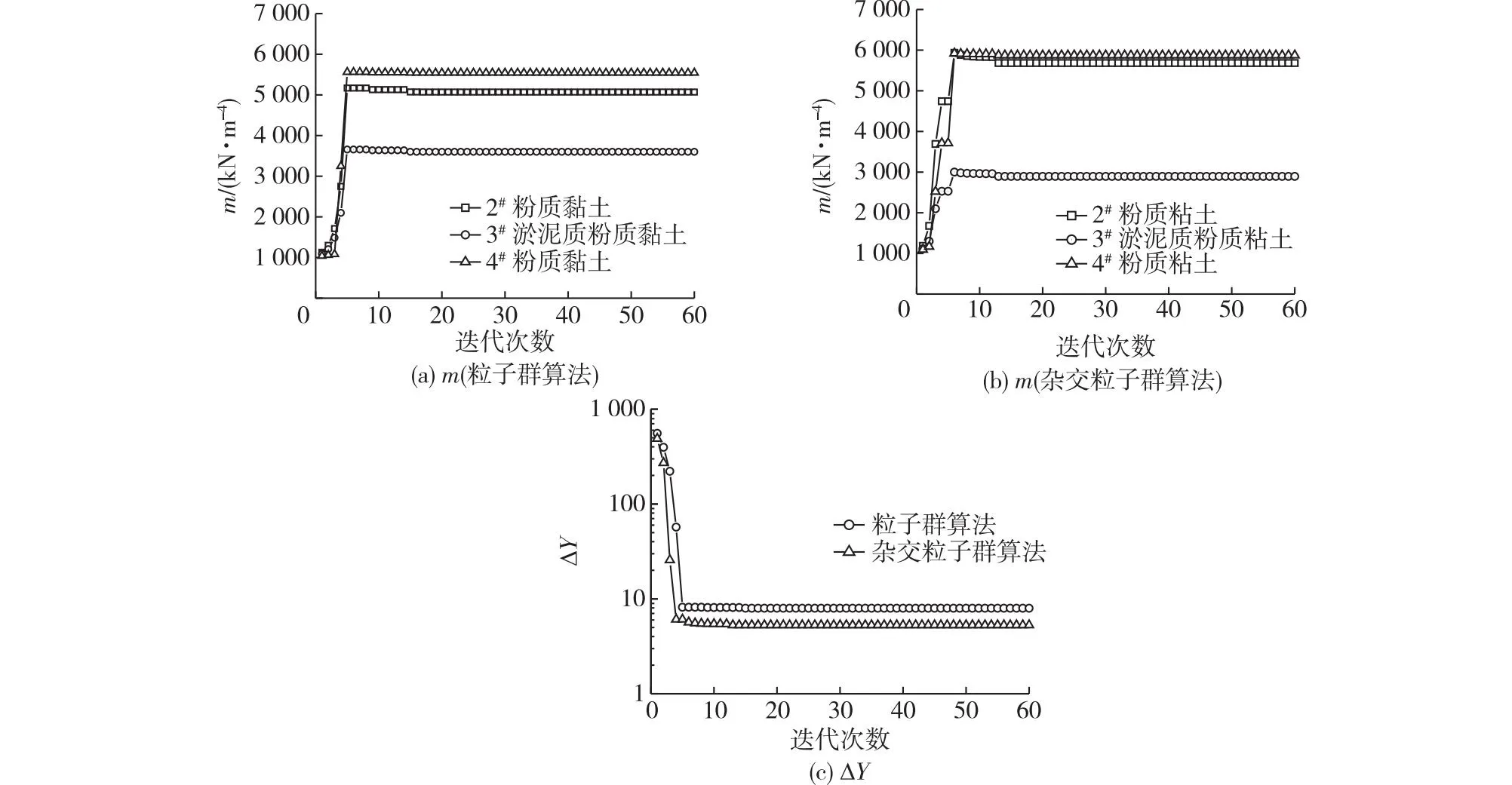
图6 多层地基土的m和ΔY收敛过程(基坑开挖至-4.0 m)Fig.6 Convergence process of m and ΔY of multi-layered foundation soil (excavation to -4.0 m)

多层地基土的m反演值见表4。由表4可知:2种最优化方法得到的m都能较好地反映土性的不同,其m反演值的大小与土的强度参数相匹配。尽管2种最优化方法得到的同一种土的m值存在差异,但都在规范[2-4]给定参考值的合理取值范围内。由此可见,不同最优化方法得到的最优解也存在差异,多参数反演问题存在多解性。依据目标函数值和收敛迭代次数判断,杂交粒子群算法在计算效率和计算精度上都具有一定的优势。此外,满足相同收敛精度要求时,多参数反演的迭代次数较单参数反演迭代次数有所增加。

表4 多层地基土的m反演值

3.2.3 基于m反演值的基坑变形预测

利用杂交粒子群算法得到的地基土m反演值和基坑支护结构杆系有限元模型,分别对基坑开挖至-4.0和-10.0 m时支护桩水平位移进行计算分析,计算结果如图7所示。

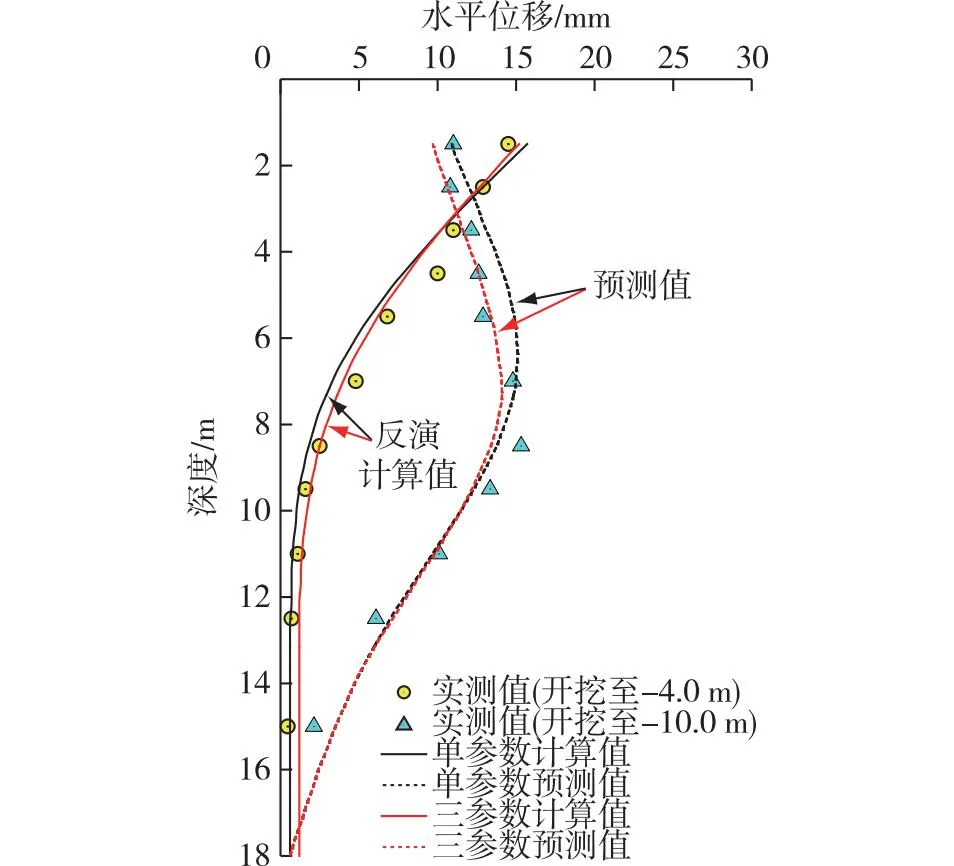
图7 基坑支护结构水平位移Fig.7 Horizontal displacement of supporting structure in excavations

由图7可知:基坑开挖至-4.0 m时,支护桩水平位移计算值与实测结果的一致性良好,表明了杂交粒子群算法反演得到的地基土水平抗力比例系数的准确性,合理反映了地基土的水平抗力特性。

地基土的m反演值的目的是合理计算支护结构的水平位移,利用m反演值对基坑开挖至-10.0 m时的支护结构水平位移进行正分析预测,水平位移预测值与实测值吻合良好,表明了基坑工程中利用前期工况监测数据反演的地基土m值适用于后续相邻施工工况变形预测,预测值合理反映了基坑开挖至-10.0 m时支护桩的实际工作性状,可为基坑工程的信息化施工提供依据。

由图7还可知:无论是均匀地基土(单参数)还是多层地基土(三参数),水平位移计算值与实测值之间均具有良好的一致性,说明了2种计算模型均能较好地反映支护结构的变形特性。因此,对于土层性质差异不大的多层地基,将地基假设为均匀地基进行支护结构水平位移计算也是合理可行的,既能满足工程实践要求,又简化了计算过程、提高了计算效率。对于土层性质差异明显的多层地基,采用多参数模型更为合理。

4 结语

1) 地基土水平抗力系数的比例系数是基坑工程中支护结构水平位移计算的重要参数,结合支护结构变形实测值和有限元法,提出了基于粒子群算法的地基土水平抗力比例系数反演计算模型,提高了计算效率,实现了水平抗力比例系数的多参数反演。

2) 提出了基于水平抗力比例系数和目标函数精度双控的反演计算收敛条件,给出了连续满足收敛条件次数的水平抗力比例系数最优解稳定条件。由于最优解稳定条件建立在算例计算结果的经验总结之上,缺乏理论依据,因此其合理性还有待进一步验证和研究。

3) 利用算例验证了水平抗力比例系数反演计算模型的正确性和m反演值的准确性,对比分析表明,引入交叉策略的杂交粒子群算法具有更高的计算效率和计算精度,工程实例分析进一步表明了水平抗力比例系数反演计算模型的工程适用性和反演结果的合理性,水平抗力比例系数反演分析能为基坑工程变形预测和信息化施工提供支持。