项目式学习对高一学生数据分析素养影响的实证研究

吴子昊，吴茎洁

（1. 上海市曹杨第二中学，上海 200062；2. 华东师范大学第一附属中学，上海 200086）

一、问题提出

在《普通高中数学课程标准（2017 年版2020 年修订）》（以下简称《2020 修订版课标》）中数据分析素养被列为六大数学学科核心素养之一。①中华人民共和国教育部：《普通高中数学课程标准（2017 年版2020 年修订）》，人民教育出版社2020 年版，第7 页。与数据分析素养最相关的数学内容为概率与统计，而我国的概率统计教育在21 世纪初期比较缺失，学生对于随机现象的理解较差。②张饴慈：《中学教育里的概率与统计》，《数学通报》2006 年第12 期，第17-21 页。经过多次课程改革，概率统计内容在我国中学数学课程中的地位得到了明显的提升，我国数学课程越来越重视学生数据分析素养的培养③史宁中，张丹，赵迪：《“数据分析观念”的内涵及教学建议——数学教育热点问题系列访谈之五》，《课程·教材·教法》2008 年第6期，第40-44 页。，这与新课程标准下的数学课程改革需求相契合。课程改革的目标不仅需要嵌入或增添概率统计教学内容，还旨在通过多样的学习方式培养学生对随机现象的理解，渗透整理、定量分析、推断数据的意识和能力，以达到对数据分析素养的有效培育。

学科核心素养的培养不仅可以在课堂教学中得到落实，还可以通过整合、开发丰富的课程资源，使学生在真实情景中学习得到素养的提升。项目式学习（Project-Based Learning，简称PBL）即是一种基于真实情境的学习方式，PBL 对数学核心素养（或能力）在一定程度上具有促进作用，主要集中于数学建模、数学运算、直观想象以及数据分析这四个领域。④何声清，綦春霞：《国外数学项目学习研究的新议题及其启示》，《外国中小学教育》2018 年第1 期，第64-72 页。从学科知识的特征来看，与数据分析素养高度相关的概率统计是一门兼具理论性与应用性的学科，与日常生活紧密相关，这个领域具有更强的情境性和直觉性，从理论上说应对PBL 有良好的适应性。①S. Sharma，“Cultural Influences in Probabilistic thinking”，Journal of Mathematics Research，Vol.4，no.5（2012），pp.63-77.从已有的研究来看，PBL 确实可以对概率统计内容的学习产生积极的影响。②T. Koparan，B. Güven，“The Effect of Project-Based Learning on the Statistical Literacy Levels of Student 8th Grade”，European Journal of Educational Research，Vol.3，no.3（2014），pp.145-157.相关研究多集中于国外，而国内缺少主题为PBL 对学生数据分析素养影响的相关研究，在现阶段国内PBL 领域中课程的建设、开发、实施等环节并不成熟，课程体系亟待完善。③李林，邹子韬，苏晓虎，潘慧明：《指向核心素养的项目式学习课程建设与实施》，《现代教育》2019 年第3 期，第20-23 页。基于数据分析素养培育的PBL 课程具有广阔的研究与开发前景。本研究以上海市的高一学生为研究对象，通过设计实施概率统计PBL 课程，聚焦参与PBL 的高一学生与未参与PBL 的高一学生在数据分析素养上的表现差异，通过实证数据，为一线教师培养学生数据分析素养以及改善概率统计内容的教学提供实践依据。

二、概念界定

1. 数学PBL

在国外，美国巴克教育研究所（Buck Institute for Education）清晰地界定了PBL 的概念：它是一种以课程标准为核心的系统的教学方法，这是一个学生面对精心设计的项目或任务，从而对一系列复杂、真实的问题进行探究的过程，学生在这一过程中以小组为单位规划项目目标，执行项目计划，最终设计出项目作品。④巴克教育研究所：《项目学习教师指南——21 世纪的中学教学法》，教育科学出版社2007 年版，第4 页。数学PBL 在PBL 的基础上加入了学科背景，使其蕴含数学学习的特质。与PBL 类似，数学PBL 也是一套系统教学法，它是对复杂、真实的数学问题的探究过程，同时也是设计数学项目任务、规划并实施、精心制作项目成果的过程。⑤薛红霞：《PBL 下数学项目化实验教材的编写与实践》，《教育理论与实践》2016 年第8 期，第42-44 页。⑥徐斌艳：《学科教学中学习文化的培育》，《开放教育研究》2007 年第4 期，第19-22 页。

2. 数据分析

《2020 修订版课标》将数据分析界定为：数据分析是指针对研究对象获取数据，运用数学方法对数据进行整理、分析和推断，形成关于研究对象知识的素养。⑦中华人民共和国教育部：《普通高中数学课程标准（2017 年版2020 年修订）》，人民教育出版社2020 年版，第7 页。基于国内外学者对数据分析内涵的讨论可以发现数据分析、数据收集、数据整理、推理判断是数据分析素养最主要的内涵。本研究将数据分析素养内涵界定为三大核心维度，并由此展开对学生的数据分析素养的调查，具体如下：对不同的研究问题进行数据的收集，即数据的收集；对收集得到的数据运用各类统计分析方法对数据进行整理与分析，即数据的整理与分析；最后用数据对研究对象进行推理、判断、解释说明，形成相关知识，即推理判断。

三、研究设计与实施

1. 研究假设

以PBL 进行“综合与实践”领域的学习，到了高中则演变为“数学建模活动与数学探究活动”，其内核都是真实情境下的问题解决，重要作用包括发展学生核心素养，强化学科关联，增强课程的综合性和实践性。⑧郭衎，曹一鸣：《综合与实践：从主题活动到项目学习》，《数学教育学报》2022 年第5 期，第9-13 页。从这个意义来说，高一学生进行PBL，不仅可以为后续开展数学建模活动做好铺垫，还可以有效落实核心素养的提升。研究假设：概率统计PBL 课程能有效提升学生的数据分析水平，发展其数据分析素养。

2. 研究对象

选取上海市某普通高中高一学生作为研究对象，其中参与PBL 课程的学生25 人，不参与PBL 课程的学生50 人，共75 人。由于两类学生的样本数量差较大，研究将分别对他们进行前测并比较均分、标准差等统计量，以观察其是否满足准实验研究的条件。

3. 研究问题与方法

研究旨在以PBL 理论为依托，设计并实施了概率统计PBL 课程，并对课程进行评价、反馈。同时基于文献的梳理，提炼出数据分析素养主要维度，开发水平框架，编制测试题并将其运用于高一学生数据分析素养的调查中。探究PBL 对高一学生数据分析素养的影响，并提出培养学生数据分析素养的教学策略。研究将聚焦于关键问题：PBL 对高一学生数据分析素养有怎样的影响，即参与PBL 的高一学生数据分析素养表现如何？未参与PBL 的高一学生数据分析素养表现如何？

研究主要采用准实验研究法以及调查研究法。准实验研究法涉及概率统计PBL 课程设计与实施，观察记录学生从设计项目任务、规划并实施，到最后精心制作出项目成果的一系列过程；调查研究法涉及PBL 后的数据分析素养调查，运用SPSS 统计软件对问卷调查得到的数据进行相关性分析。

4.PBL 课程的设计

研究基于PBL 理论以及高一学生自身认知与数学知识基础，设计并实施5 个旨在培养学生数据分析素养的概率统计PBL 活动，提供若干驱动问题供学生小组选择并进行研究。

活动一：数学，让我欢喜让我忧

所需数学知识或能力：抽样统计，数据的收集、整理、分析。

活动二：一起撒豆子，扔牙签

所需数学知识或能力：几何概型，随机试验，测量与读数，数据处理及误差分析。

活动三：我们现在使用的键盘合理吗

所需数学知识或能力：频率与概率，样本估计总体，统计图表的绘制。

活动四：神奇的高尔顿钉板

所需数学知识或能力：二项分布，正态分布，大数定律。

活动五：不可思议的本福特定律

所需数学知识或能力：抽样统计，概率分布，对数函数。

5 个活动的开展均需要概率统计知识作为理论基础。

5. 素养水平框架的搭建与测试卷的编制

素养水平框架主要分为维度水平框架和综合水平框架。

（1）维度水平框架

基于SOLO 分类法①吴有昌，高凌飚：《SOLO 分类法在教学评价中的应用》，《华南师范大学学报（社会科学版）》2008 年第3 期，第95-99 页，第160 页。，结合数据分析素养各个维度思维特点的复杂性将其水平划分为不同的层次，现提出数据分析素养维度水平的概念，其定义是：数据分析素养各维度表现出来的水平，分为最低水平、中间水平、最高水平。

（2）综合水平框架

根据个体的数据分析素养不同维度水平的组合可得到其数据分析综合能力与素养水平。个体的数据分析素养（能力）是随数据分析素养结构复杂性呈现层次变化的，且这种层次变化是循环出现的，可将其划分为水平1、2、3（见表1）。

表1 综合水平框架

本研究基于上述框架编制测试卷。试卷依据《2020 修订版课标》中对于数学问题的分类，选取三类情境，分别是现实情境、数学情境、科学情境，并依据3 个情境依次设置了3 道大题。在题目内容方面，每道大题下属都有3 个小问题，分别对应学生在解决数学问题时体现出的数据分析素养的3 个维度，其难度依次递增。题目不涉及明显的、记忆性的概率统计知识与相关数学概念，以免学生可凭题目所给材料与信息推断出所有答案。题型包括填空题、选择题、解答题。测试卷旨在调查学生脱离具体知识内容的数据分析素养与能力。测试卷考查的重点依次对应先前提炼出的3 个数据分析内涵维度，题目难度及考查的数据分析素养维度水平呈阶梯状递增。

6.PBL 课程与测评的实施

2022 年9 月，设计并实施时长为10 课时，为期5 天的概率统计PBL 课程。为了分析PBL 对学生数据分析素养的影响，研究选取平行班级作为对照班，对他们进行常规的概率统计教学与同样的数据分析素养调查。参与PBL 课程的学生群体为A 班，未参与PBL 课程的学生群体为B 班。为保证研究的相对准确性，在研究开始时选取2009 年PISA 测试中涉及统计素养的8 道实测题①李俊，黄华：《PISA 与上海中考对统计素养测评的比较研究》，《上海教育科研》2013 年第12 期，第39-42 页。对A 班与B 班学生进行前测，发现两班表现相当，可认为A 班与B 班的数据分析素养水平大致相同，基本符合准实验研究的条件。

A 班25 名学生被平均分为5 组，各小组选择一个项目活动进行学习和探究。在PBL 活动中，某些项目仅仅依靠学生现有的知识能力是不够的。出现这种情况时，学生的内部动机可能会受到影响，对自己的能力产生疑问。因此，需要让学生意识到：在PBL 中除了使用已经熟悉的学科工具，还应该正视陌生的问题，请求专家帮助或者进阶学习，最终以某个有形的作品呈现活动结果。②徐斌艳：《数学素养与数学项目学习》，华东师范大学出版社2021 年版，第54 页。课程具体安排见表2。

表2 PBL 课程安排

在活动过程中，各小组成员分工协作，一起确定活动目标、设计活动过程、制作活动成果、交流展示成果的过程。以第二小组为例，第二小组探究活动为“一起撒豆子，扔牙签”。学生依据几何概型设计了两个随机试验来估算圆周率π的数值。

其一是投掷绿豆试验。由于圆面积和圆外切正方形面积的比值等于随机掉下的绿豆落在圆内的概率比落在圆外切正方形内的概率，即：

根据此原理，小组成员设计并实施了投掷绿豆试验，在一边长为20cm 的正方形区域内均匀撒豆，采取两种办法（分别测得绿豆的数量和重量）得到了一系列圆周率π的近似值。接着，小组成员对结果进行误差分析并改进试验，进一步使用米粒进行试验，得到更精确的数据。

其二是蒲丰投针试验。小组成员设计并再现了18 世纪数学家蒲丰依靠随机投针法计算圆周率的经典试验。根据蒲丰投针试验的原理①1777 年，法国数学家蒲丰正式提出“投针问题”：在平面上画有一组间距为a 的平行线，将一根长度为L（L≤a）的针任意掷在这个平面上，求此针与平行线中任一条相交的概率。蒲丰通过微积分证明了这个概率为：其中π 为圆周率）。由于它与π 有关，于是就利用投针试验来估计圆周率的值。蒲丰惊奇地发现：如果使得针的长度等于，那么扔出的概率为扔的次数越多，由此能求出越为精确的π 的值。，当牙签长度L与平行线间距d的关系满足L= 0.5d时，得出：

根据此结论，小组成员分别投掷了50 根、217 根牙签，得到了圆周率π的近似值。学生还试验了不同数量的平行线（4 根、5 根、11 根），试验发现平行线数量对结果并无影响。

在PBL 课程结束之后，分别对A、B 班进行施测，两个班级的测试过程与要求保持一致，测试时间为40 分钟，共收回有效问卷70 份，其中A 班23 份，B 班47 份。对测评结果进行编码，运用统计分析软件SPSS 对数据进行描述统计、信度以及方差分析。在分析之前首先对测试题进行Cronbachα系数计算，得出量表的信度达到0.786，说明试卷各条目之间的一致性较好，具有一定的同质性信度。运用KMO检验法得到测试题的KMO 值为0.692，表明是可以接受的，试题具有较好的效度。

四、研究结果

1.A 班与B 班数据分析素养调查结果比较分析

根据测评结果的编码数据，A 班与B 班学生在数据分析素养各维度的表现与得分情况分别见表3。A 班学生在“数据的收集”“对数据的整理与分析”上要优于B 班学生，体现出更强的对数据收集、整理、分析的能力。在“推理判断”维度上，两类群体表现均不理想，能力较弱。

表3 各维度得分情况

2.PBL 对高一学生数据分析素养的影响分析

效应量是一种度量效应大小的指标，效应量具有与测量单位无关、单调性、不受样本容量的影响等基本性质。②温忠麟，范息涛，叶宝娟：《从效应量应有的性质看中介效应量的合理性》，《心理学报》2016 年第4 期，第435-443 页。效应量可以解决P 值无法刻画相关程度大小和差异大小的问题。③王光明，李健，张京顺：《教育实证研究中的P 值使用：问题、思考与建议》，《教育科学研究》2018 年第2 期，第59-65 页。在教育研究的统计推断中引入效应量，对于提高教育研究的科学性具有重要意义。研究采用效应量来刻画PBL 对高一学生数据分析素养的影响。采用赫奇斯（Hedges）对效应量的计算定义，其中Hedges 的d 评价标准参考科恩（Cohen）的ds标准④J. Cohen，“Statistical Power Analysis”，Current Directions in Psychological Science，Vol.1，no.3（1992），pp.98-101.，计算结果为0.2，表示有效应且效应量较小；计算结果为0.5，表示有中等的效应；计算结果为0.8，表示效应非常显著。

（1）维度分析

对于“数据的收集”“对数据的整理与分析”这两个维度，效应量d分别达到了0.392、0.384，介于小效应（0.2）与中效应（0.5）之间，说明PBL 对这两个维度都产生积极的效应，效应量介于“较小”和“中等”之间，其中对“数据的收集”维度的促进作用略强于“对数据的整理与分析”维度。对于“推理判断”维度，效应量d 为-0.086，是负效应，取绝对值之后|d|=0.086，数值非常小，未达到小效应标准（0.2）。

（2）情境分析

用同样的方法研究问题情境的效应量见表4。对于现实情境与数学情境，效应量d 分别达到了0.253、0.290，属于小效应（0.2），说明PBL 对这两种情境的问题都产生积极的效应。其中对数学情境的促进作用略强于现实情境。对于科学情境，效应量d 为-0.091，是负效应，取绝对值之后|d|=0.091，未达到小效应标准（0.2）。

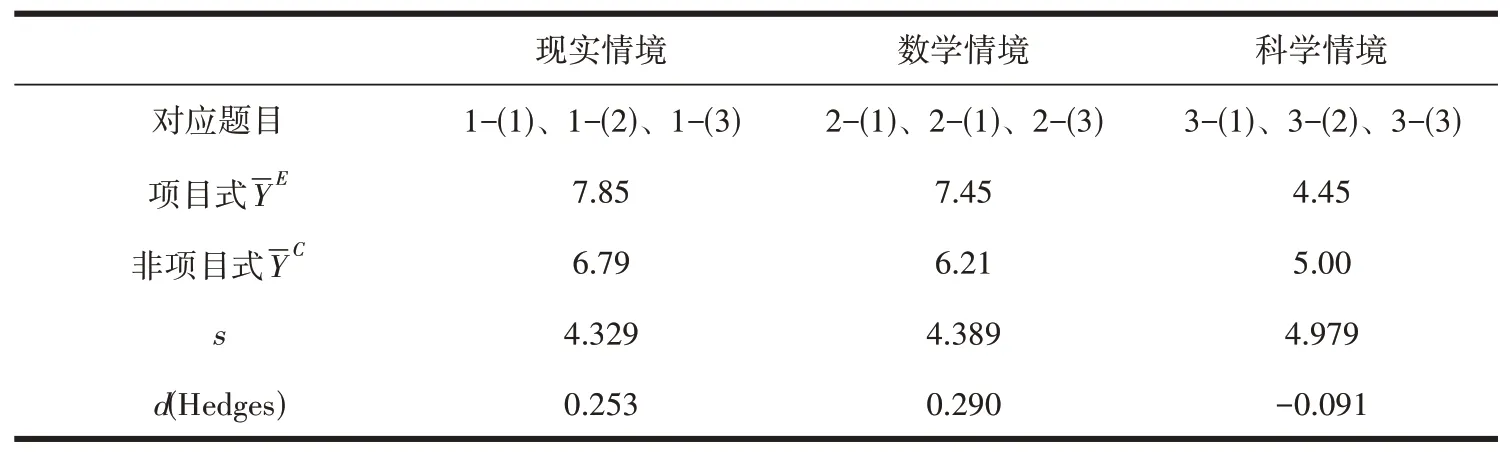
表4 各问题情境效应量大小

3. 数据分析素养水平分布

将数据分析素养各个水平的思维特点具化为测试题的评分，得到素养水平评分编码表。总分分别达到6、21、45，则认为数据分析素养分别达到水平1、2、3。对调查试卷进行逐一编码、赋分、一致性检验等操作，得出被试样本的数据分析素养水平分布。表5 展示了A 班学生和B 班学生的数据分析素养水平分布。A 班学生达到数据分析素养水平1、水平2 的比例均超过了B 班学生，分别超出5.94 和2.34个百分点，水平1 的比例差异最大。且在未达到最低水平的学生比例中，A 班学生低于B 班学生5.02个百分点。

表5 数据分析素养水平分布

五、研究结论

1.PBL 能有效提升高一学生数据分析素养

结果显示，参与PBL 课程的高一学生在数据分析素养总体表现上优于未参与PBL 课程的高一学生。参与PBL 课程的高一学生达到水平1 与水平2 的人数比例高于未参与PBL 课程的高一学生。通过对“效应量”的分析可知，在维度方面，概率统计PBL 课程可以较好地促进数据分析素养中较为基本的能力，主要包括数据的收集、整理、分析；在问题情境方面，概率统计PBL 课程对学生解决具有现实背景或是纯数学背景的问题有较好的促进作用。

2.PBL 有助于将概率统计知识迁移至活动过程中

经过对概率统计PBL 课程的设计、实施、评价、反馈可以总结出，旨在培养高一学生数据分析素养的PBL 课程具有小组探究、多样的成果形式、多种评价方式相结合等特点，项目活动以其多样性、情境性为学生提供了一个广阔的学习平台，使学生在分析与解决问题的过程中融合新知识、新技能。活动较好地将概率统计知识迁移至项目推进过程中，学生在每个项目活动中都运用了统计方法，对数据中的有用信息进行收集、整理、分析、推断，培养了数据分析素养。

本研究设计的概率统计PBL 课程以其情境性契合高一学生的认知基础，较好地促进了高一学生的数据分析素养水平，尤其对数据分析素养中基础能力（数据的收集、整理、分析）的提升有较好的效果。建议教师在概率统计教学中适当引入PBL 活动，在教学中重视情境的创设，通过挖掘丰富的实际案例，将数学知识内隐于情境中，通过将现实问题抽象为数学问题进而建立数学模型的过程，催化数学项目活动，培养学生用数学知识解决实际问题的能力，感受数学的应用价值。同时我们也应注意，在设计PBL课程时应尽量避免项目活动通常会带来的知识离散化、碎片化问题，尽量使知识的传授具有其原有的逻辑体系。