基于扩展卡尔曼滤波的传感器融合SLAM研究

杜俊峰,郁汉琪,刘义亭,张 昊

(南京工程学院,江苏 南京 211167)

0 引言

在当今世界,自主移动机器人技术的发展正以前所未有的速度蔓延到多个领域,如自动驾驶汽车、无人机、扫地机器人等多种自主移动导航系统[1],这些机器人需要准确的导航和地图构建技术,以适应各种环境完成任务。SLAM是指移动机器人在未知环境中从未知位置移动[2],它在移动过程中根据位姿估计和传感器数据进行自我定位,同时创建增量地图,SLAM技术的研究已经成为移动机器人定位导航领域的热点,基于多传感器融合的定位方法引起了广泛研究,也是实现机器人真正自主运动的关键。

尹皓等[3]提出一种基于高斯牛顿方程的多传感器非线性融合定位算法,但存在运算量大、运行速度慢等问题;朱忠祥等[4]提出了一种基于置信度加权的组合导航融合定位方法,但计算较复杂;何珍等[5]提出了一种视觉与激光雷达组合的导航定位系统,有效提高了定位精度,但相机的工作环境要求较高且计算复杂。Zhang等[6-7]提出利用二维码辅助定位,用激光雷达辅助避障算法,有效提高了定位精度,但是需要提前布置二维码路标,应用场景局限。

针对上述问题,本文以履带式机器人为对象,建立了机器人运动学模型,提出了通过线性变换函数的方法和用IMU角速度作为里程计角速度的方法来减小履带运动误差,利用扩展卡尔曼滤波融合里程计和IMU数据的方法减小机器人累积误差。最后搭建了里程计的误差测试实验和不同场景下的SLAM建图实验,本文改进后的里程计误差降低了91.72%,且SLAM地图更加完整准确,验证了本文算法的可行性与可靠性,提高了机器人定位精度。

1 算法设计

1.1 履带式机器人运动学模型

本文使用的机器人为履带式结构,单侧驱动轮只有一个,建立运动学模型时对机器人做出以下2个假设:(1)机器人履带运动时与地面不发生相对滑移。(2)机器人质量分布均匀且质心位于几何中心;其运动学模型可以简化等效成两轮差速驱动机器人模型[8]。选取几何中心作为原点O建立右手坐标系,机器人向前运动方向为x轴正方向,垂直x轴向左为y轴正方向,垂直xOy平面向上为z轴正方向,如图1所示。其中机器人轮距为L,转弯半径为R,右轮到圆心距离为D(假设机器人此时向右做移动转向运动),机器人运动线速度为v,角速度为ω。

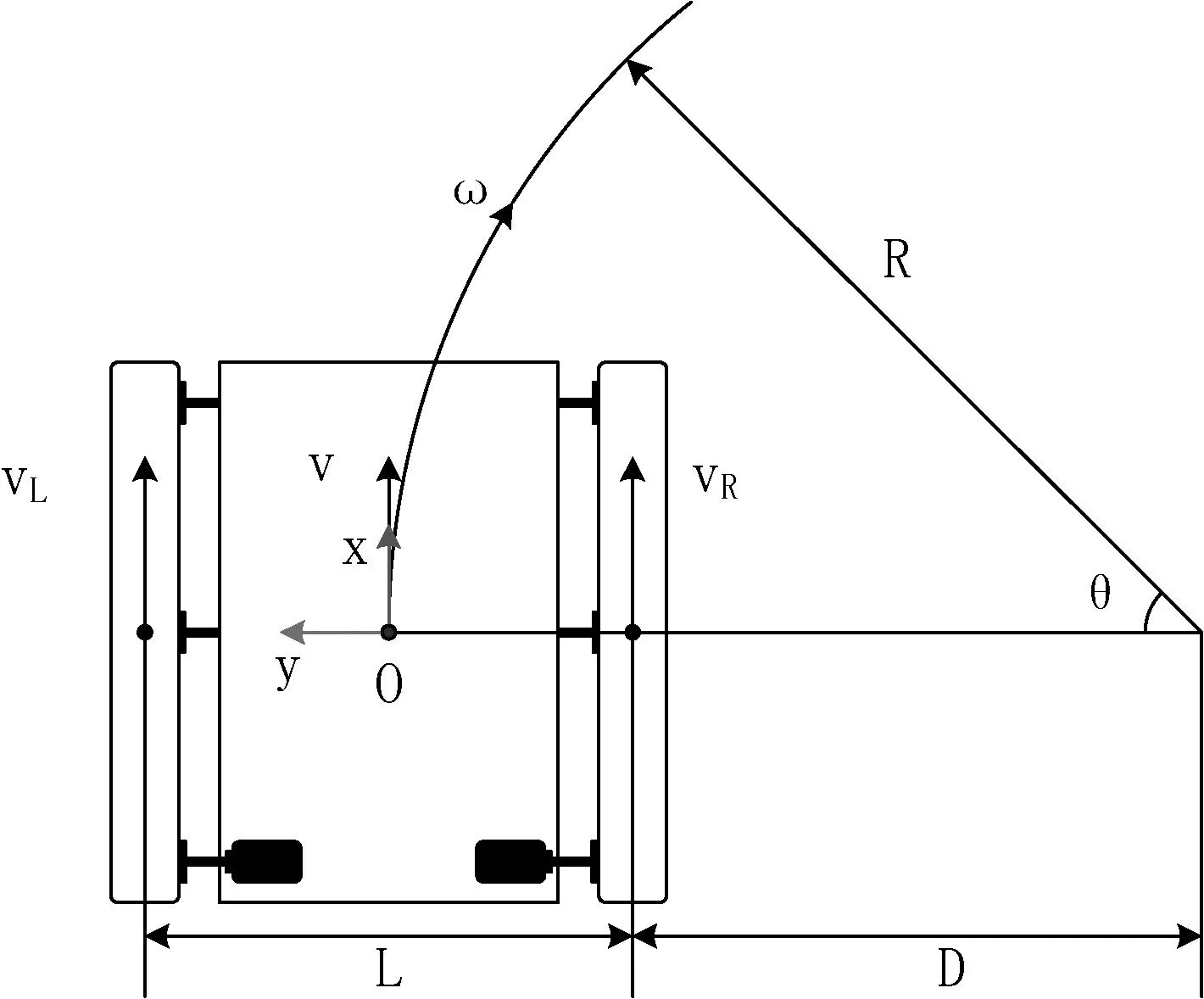
图1 履带机器人运动学模型

机器人运动线速度v的解算如式 (1)。

(1)

机器人左轮运动速度vL、右轮运动速度vR的求解如式 (2)。

(2)

由式 (2)可以得到机器人运动角速度ω如式 (3) 。

(3)

式 (1)和式 (3)为机器人正运动学公式,写成矩阵形式为:

(4)

对式 (4)中系数矩阵求逆运算可以得到机器人的逆运动学公式,如式 (5)。

(5)

在机器人运动控制过程中,正运动学公式可以描述为根据左右轮转速计算得到机器人的线速度和角速度,逆运动学公式可以描述为向机器人发送线速度和角速度数值,解算成左右轮转速。里程计是在正逆运动学基础上,配合航迹推演算法来确定机器人的位姿信息P,包括了x轴坐标X、y轴坐标Y和航向角θ,与机器人线速度v、角速度ω的关系由式 (6)确定。

(6)

将式 (6)在时间t上进行积分就可以求出底盘实时位姿,也就是里程计信息。实际情况下,需要在离散时间域上进行计算,由于底盘相邻两位姿相隔时间Δt很小,积分运算可以用式 (7)的累加运算来替代。

Pt=Pt-1+PΔt

(7)

1.2 线性变换法

针对直线运动过程中的履带滑移现象,本文采用实验逆推法求取线性变换函数。首先移动机器人,分别记录下机器人里程计值和使用激光测距仪所测的实际位移,然后利用MATLAB函数拟合工具箱,将机器人里程计值作为输入x,实际位移作为输出y,进行直线拟合,最后拟合得到的函数图像如图2所示。

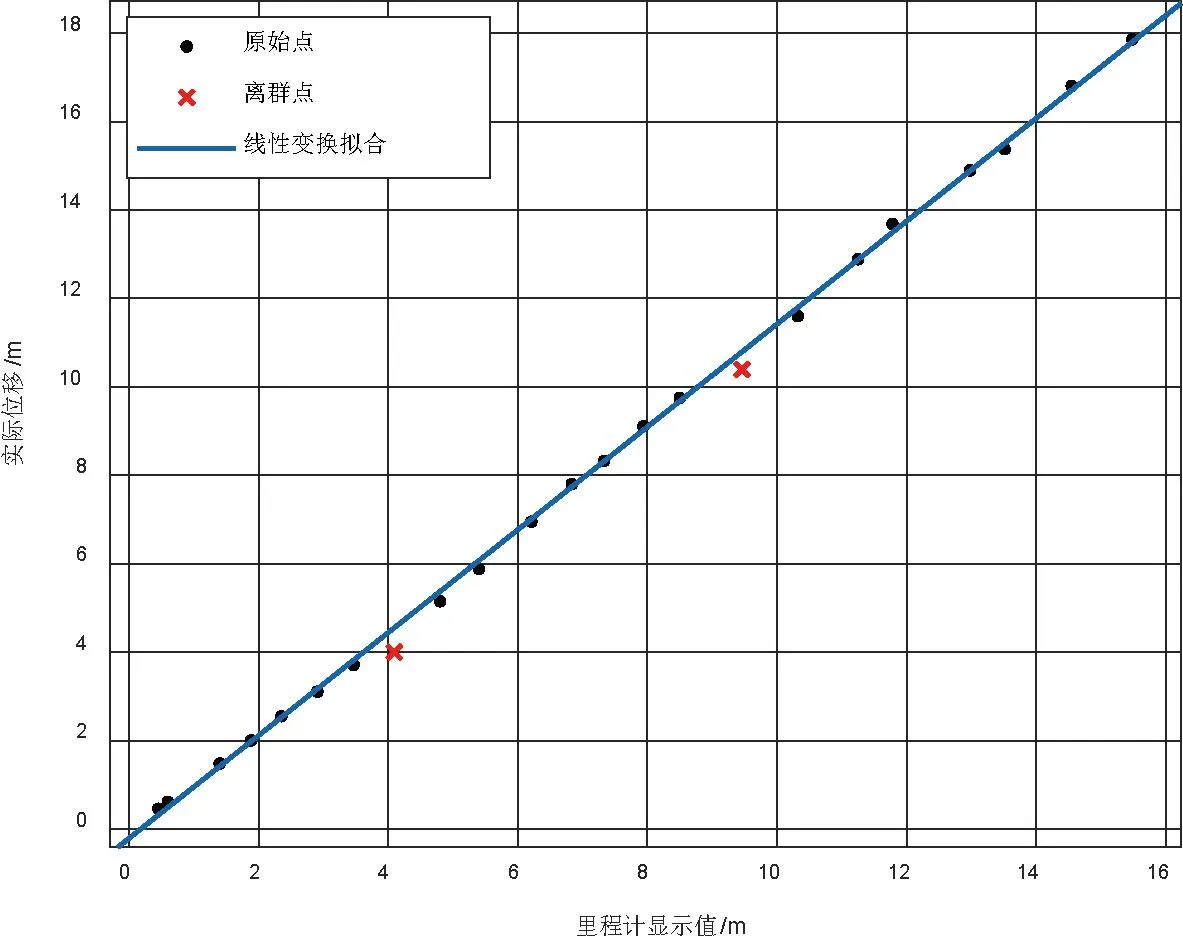
图2 线性变换函数拟合

手动剔除掉离群点,最终确定的线性增益函数如式 (8)所示。

f(x)=1.155x-0.1857, (|x|≥0.1608)

(8)

里程计模型中的角速度ω由左右两轮速度差和轮距计算得来,但是机器人在实际转向运动过程中,机器人质量分布不均匀、与地面发生不同程度的滑移和编码器精度较低等因素都会增大里程计航向角的累积误差,严重影响机器人的定位。针对角速度ω的误差修正,提出融合IMU的方法:先利用低通滤波对IMU原始数据进行滤波,然后使用IMU角速度ω′作为里程计计算过程中的角速度ω,新的里程计位姿P′的计算方式如 (9)。

(9)

1.3 EKF多传感器融合

为了进一步减小里程计的累积误差,提高机器人的定位精度,本文使用扩展卡尔曼滤波对里程计和IMU进行多传感器融合,k-1时刻机器人里程计数据输入的位姿估计为xk-1=[xk-1,yk-1,θk-1]T,由xOy平面上x轴坐标、y轴坐标以及机器人的航向角确定。

系统状态方程描述为:

xk=f(xk-1,uk)+wk

(10)

其中,xk是系统在时刻k的状态向量,f为非线性状态转移函数,uk为控制输入量,wk为过程噪声。系统测量方程描述为:

zk=h(xk)+vk

(11)

其中,zk是在时刻t测量得到的观测向量,h是非线性观测模型函数,vk是测量噪声。初始状态估计为:

(12)

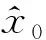
(13)

(14)

其中,Fk为状态转移矩阵的雅可比矩阵,Qk为过程噪声的协方差矩阵。k时刻的卡尔曼增益Kk为:

(15)

其中,Hk是观测模型的雅可比矩阵,Rk是测量噪声的协方差矩阵。

最后,更新卡尔曼滤波状态,将计算得的最优状态向量xk设为下一次计算中的xk-1,协方差矩阵Pk也进行同步更新,更新过程中的最优状态和协方差矩阵可以表示为:

(16)

(17)

本文使用的传感器融合算法步骤可以总结为:

步骤1 拟合一个线性变换函数来修正机器人直线移动中的里程计误差;使用IMU滤波后的角速度值作为里程计的角速度,发布初步处理后的里程计。

步骤2 通过里程计数据和IMU对卡尔曼滤波状态进行联合预测。

步骤3 计算卡尔曼增益并计算最优状态向量与协方差。

步骤4 更新卡尔曼滤波器状态与里程计。

2 实验设计与结果

2.1 硬件与软件平台

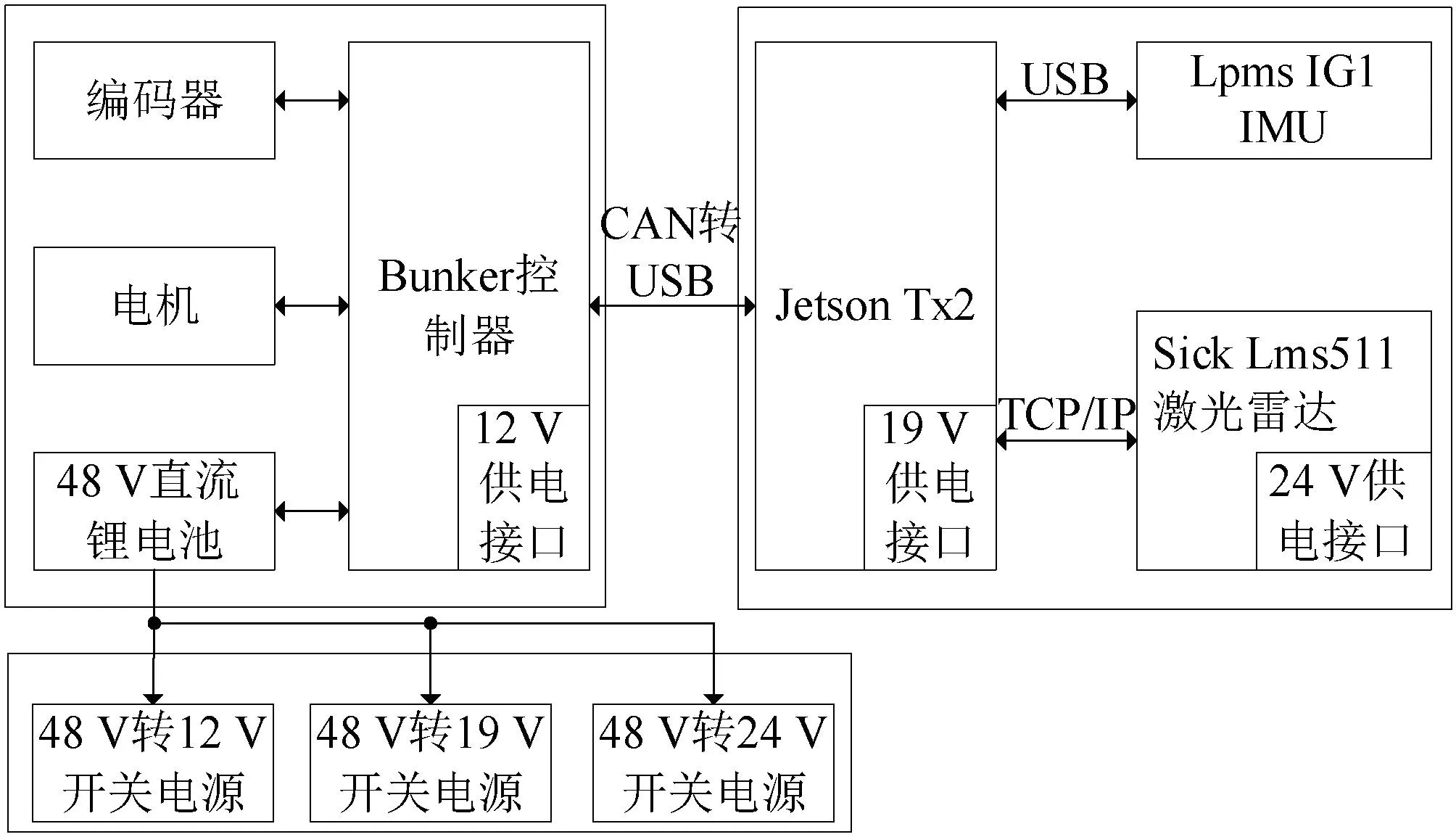
图3 硬件组成

图4 硬件组成机器人实物

软件开发环境使用以Linux为内核的Ubuntu 18.04系统,安装ROS Melodic版本机器人开发环境,Jetson TX2与本地PC通过SSH建立远程通信,运行机器人底盘与传感器等设备,完成SLAM地图构建并通过rviz可视化显示。

2.2 里程计误差实验

移动机器人从起点到距离15 m处,分别使用原始里程计模型和本文改进融合后里程计算法,每次间隔1 m记录一次激光测距仪测量机器人位置的真实值,与里程计话题数值相减得到里程计误差,对比原始误差和融合后误差,重复10次实验并记录平均值,最后的里程计误差如图5所示,里程计误差最大降低了91.72%。

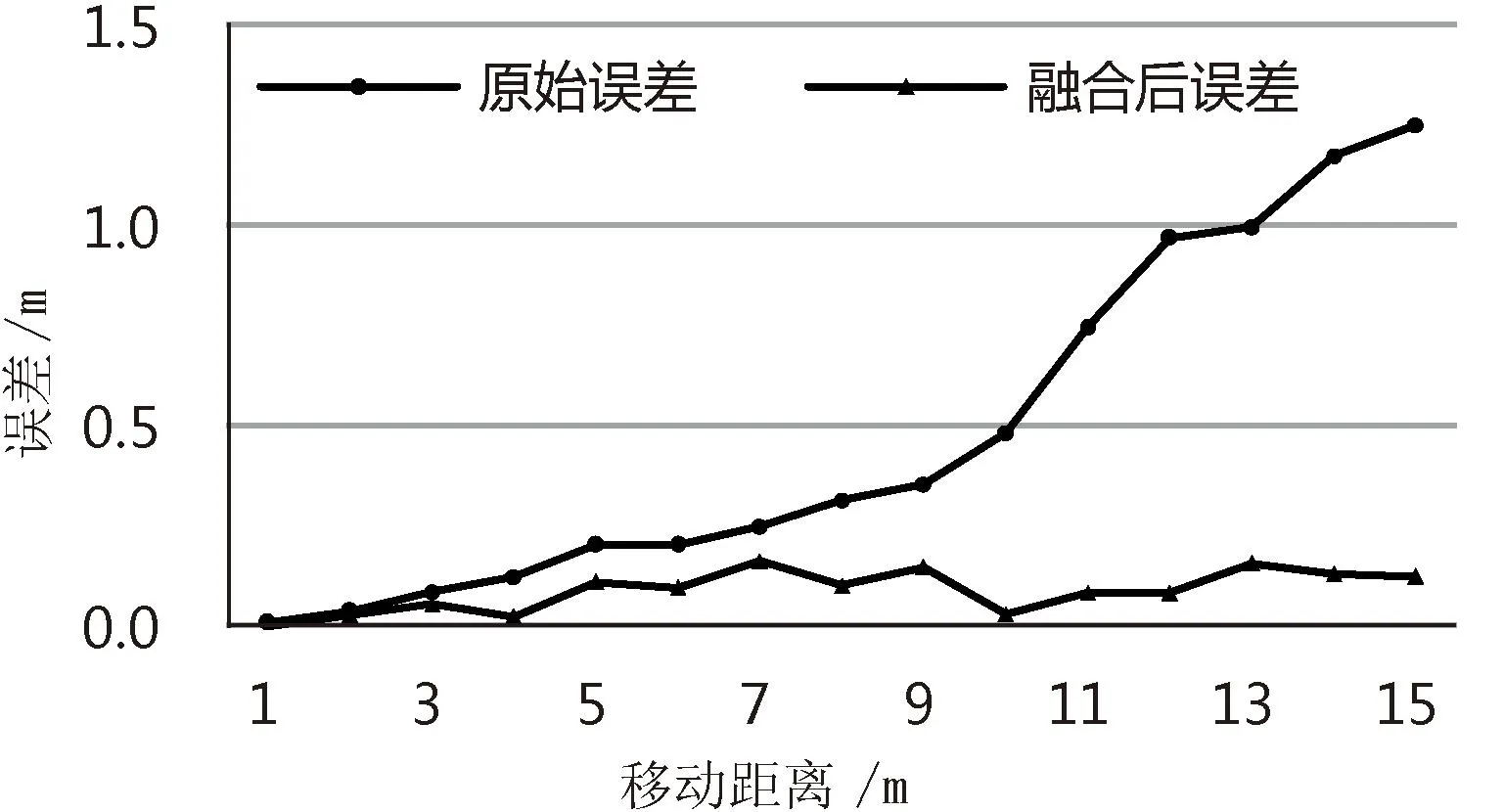
图5 里程计误差

2.3 复杂室内SLAM实验

本文选取2个场景进行实验,其一为室内实验大楼1楼,包含长廊退化环境、多角点特征环境、大范围空旷环境等;另一场景为半封闭实验楼,主要由4条长走廊组成,形成闭环。在本地PC上利用SSH远程控制Jetson TX2运行机器人程序,录制包含所有设备话题的试验数据集,其中主要有:雷达话题/scan、IMU话题/imu/data、里程计话题/odom。然后,进行SLAM对比实验,使用的SLAM算法均为Cartographer,在传感器方面,第一次使用未融合的里程计和激光雷达,第二次实验使用经本文算法融合改进后的里程计和激光雷达,所得到的实验楼地图如图6-9所示。

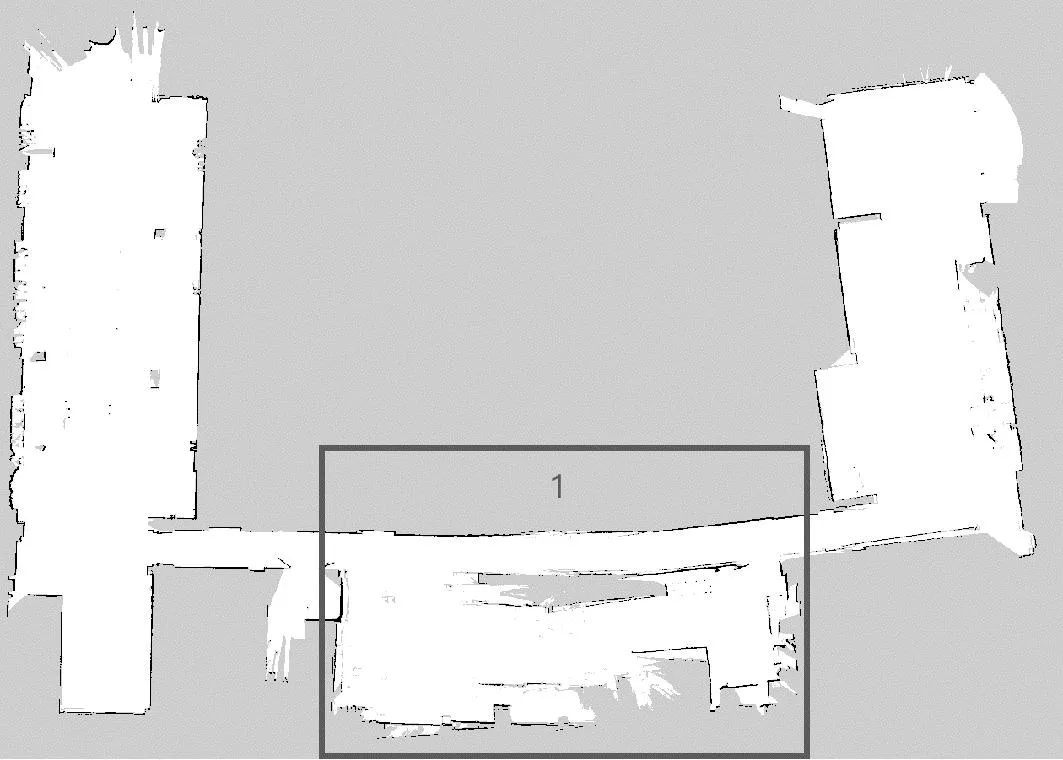
图6 场景一:未使用传感器融合的SLAM地图

在场景一下,图6区域1中,激光雷达应对长廊环境时发生退化,里程计累积误差使机器人定位丢失,构建的SLAM地图发生严重的漂移,造成地图不匹配;图7中使用本文融合多传感器改进算法进行定位和构建地图,机器人定位准确,整体地图完整,地图信息构建全面,对长廊、多角点环境以及大范围空旷地图等能良好构建出地图。在场景二下,图8构建的地图尽管能通过Cartographer后端回环进行优化,但仍然存在严重扭曲部分,无法满足SLAM的要求;图9中SLAM效果显著,提高了里程计准确性,对环境特征重现更加准确。

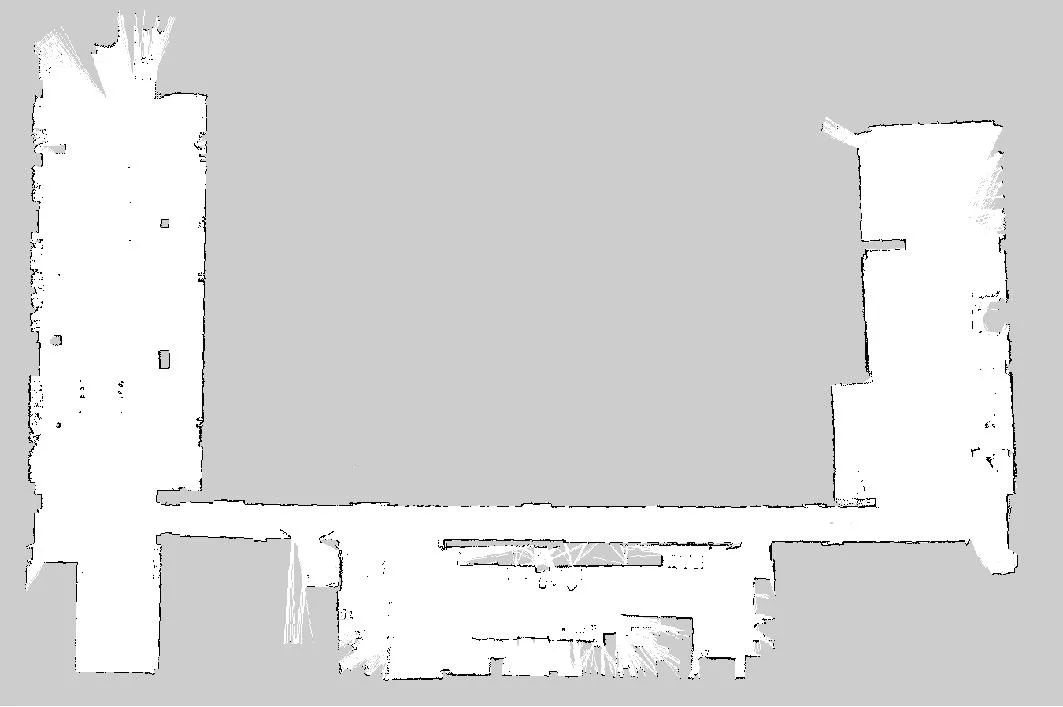
图7 场景一:使用本文算法后的SLAM地图

图8 场景二:未使用传感器融合的SLAM地图

图9 场景二:使用本文算法后的SLAM地图

3 结语

本文针对履带式机器人在SLAM过程中的里程计误差导致定位丢失问题,提出了基于线性变换函数和扩展卡尔曼滤波融合改进方法。经实验表明,该方法里程计误差最大减少91.72%,提高了SLAM过程的机器人定位精度。在未来,利用多传感器融合进行不断改进算法将是SLAM的发展方向,提高SLAM精度,才能实现真正可靠的自主导航。