Model-based assessment of muscle forces and strain distribution in the femur of Cabot’s Tragopans (Tragopan caboti)

Xinsen Wei, Zihui Zhang

aInstitute of Geology and Paleontology,Linyi University,Linyi,276000,China

bCollege of Life Sciences,Capital Normal University,Beijing,100048,China

Keywords:Cabot’s tragopan Femur Finite element analysis Inverse simulation Muscle force Strain

ABSTRACTThe hindlimbs play a crucial role in bird locomotion, making the biomechanical properties of the musculoskeletal system in these limbs a focal point for researchers studying avian behaviour.However, a comprehensive analysis of the mechanical performance within the long bones of hindlimbs during locomotion remains lacking.In the present study, the strain and deformation of the femur of Cabot’s Tragopans (Tragopan caboti) were estimated.We employed inverse simulation to calculate the force and moment of femoral muscles during mid-stance terrestrial locomotion and conducted finite element analysis to calculate femoral strain.Results showed that during mid-stance, the femur experiences combined deformation primarily characterized by torsion, bending,and compression.It emphasises the importance of considering the influence of varying loads on bone adaptation when investigating bone form-function relationships.Muscles were found to play a significant role in offsetting joint loads on the femur, subsequently reducing the deformation and overall strain on the bone.This reduction enhances femoral safety during locomotion, allowing birds to meet mechanical demands while maintaining a lightweight bone structure.Notably, the M.iliotrochantericus caudalis significantly reduces torsional deformation of the proximal femur, protecting the vulnerable femoral neck from high fracture risk induced by rotation load.Given that the femur torsion during terrestrial locomotion in birds is associated with changes in hindlimb posture due to their adaptation to flight, the characteristics of M.iliotrochantericus caudalis may provide insight into the locomotor evolution of theropods and the origin of avian flight.

1.Introduction

Hindlimbs play a crucial role in the locomotion of birds.While wings are specially used for flying, the hindlimbs are responsible for various functions in different modes of locomotion, such as walking, running,paddling, and arboreal movements (Abourachid and H¨ofling, 2012).In birds of different lifestyles, the long bones of the hindlimb can vary greatly in size, morphology, and other characteristics (Gatesy and Middleton, 1997; Zeffer et al., 2003; Habib and Ruff, 2008).The researchers studied many aspects of bird movement through hindlimbs,including the relationship between the geomorphology of bones and lifestyles (Habib and Ruff, 2008; Bell and Chiappe, 2011; Falk et al.,2021), the ontogenetic changes of the locomotion pattern (Carrier and Leon, 1990; Wei and Zhang, 2019, 2021), and the changes in appendage posture during evolution (Allen et al., 2021).Bone form, to some extent,reflects its mechanical loading history.The mechanical performance,encompassing factors like strain, stress, and deformation, provides insights into a bone’s adaptability during locomotion (Currey, 2002).Therefore, detailed studies on the mechanical performance of long bones will help to deepen our understanding of the unique adaptations that have allowed birds to achieve such a remarkable diversity of locomotor behaviours.

An accurate assessment of bone mechanical performance relies on a thorough understanding of the bone’s loading environment, i.e., conditions in which bones are loaded during locomotion.In the context of long bones, this involves a detailed examination of physiological loads,predominantly consisting of joint loads and muscle forces (Judex and Carlson, 2009).The vast majority of detailed studies on physiological load in bones have been conducted on humans.These studies involve measuring stress and strain within bones during specific sports or daily activities (Martelli et al., 2014; Khassetarash et al., 2022), as well as for medical purposes such as analysing fractures (Geier et al., 2019).In contrast, only a few investigations that have considered the mechanical performance of bones under physiological loads in animals have been published (Shahar et al., 2003; Lee et al., 2020).Regarding birds, Bishop et al.(2018) built a musculoskeletal model of the hindlimb of chickens and analysed the mechanical performance of the femur and tibiotarsus.However, the author’s focus was on the relationship between cancellous bone architecture and principal stress trajectories of long bones; the mechanical performance of the bones was not analysed in detail.Additionally, several studies have calculated the hindlimb muscle forces or muscle moment arms of birds (Smith et al., 2007; Goetz et al., 2008;Hutchinson et al., 2015; Rankin et al., 2016), none of them have measured the stress or strain of bones.Our understanding of the skeletal loading environment of birds is still limited.

An important factor that impedes the study of bone strain is the complex muscle forces on bones.Given that multiple muscles are often attached to a single bone, determining the physiological load experienced by bones presents a significant challenge.To overcome this issue,studies typically adopt optimization technologies, with inverse simulation being a commonly used method (Anderson and Pandy, 2001;Erdemir et al., 2007; Bishop et al., 2021).Measuring stress and strain within bones can also be challenging due to their irregular geometry and complex loading environment.Finite element analysis (FEA) is a powerful tool for addressing biomechanical problems related to bones.FEA allows researchers to create detailed computational models of bones, taking into account their complex geometry.These models can then be used to simulate various mechanical loads and predict stress,strain, and deformation within the bone structure, providing valuable insights into bone biomechanics (Rayfield, 2007; Bright, 2014).

In this study, we employed inverse simulation to calculate the forces and moments of the femoral muscles in Cabot’s Tragopan (Tragopan caboti) during mid-stance terrestrial locomotion.Subsequently, finite element analysis was employed to estimate femoral strain and deformation.The study aimed to clarify the loading environment and mechanical performance of Cabot’s Tragopan’s femur during locomotion,to support further study on the form-function relationship of bones and the locomotion mechanism, etc.Cabot’s Tragopan, a vulnerable species endemic to China, cannot be used in animal experiments due to its conservation status.However, comprehensive data and models are available to support in-depth research on its long bone strain.Zhang and Zheng (1996) and Wang et al.(2021) have provided detailed anatomical descriptions of the hindlimb muscles of Cabot’s Tragopan, while Wei and Zhang (2021) have built finite element models of their femora with anatomically accurate and inhomogeneous material property.These resources were crucial in conducting the present study.

To guide our analysis, we develop the following hypotheses regarding femoral loading environment and mechanical performance during mid-stance.Firstly, we test the hypothesis that the femur of Cabot’s Tragopans experiences combined loadings and deforms in complex ways during mid-stance.It has long been assumed that the limb bones of vertebrates primarily endure bending forces during locomotion, with the orientation of the diaphysis’ maximum bending rigidity often presumed to align with the direction of peak bending forces experienced by the bone (Lieberman et al., 2004).However, in vivo strain studies indicate that the diaphysis of long bones does not necessarily bend along the planes where it offers the most resistance to bending (Cubo and Casinos, 1998; Lieberman et al., 2004; Demes,2007).This suggests that long bones are subjected to a variety of loads,not limited to bending, or at least not primarily dominated by bending.Furthermore, strains observed in vivo in vertebrate long bones reveal a complex loading regimen that includes bending, torsion, tension, and compression (Biewener and Dial, 1995; Carrano, 1998; Lieberman et al.,2004; Main and Biewener, 2006; Young et al., 2017).Therefore, we predict that the femur of Cabot’s Tragopans experiences combined loadings during mid-stance.

Secondly, we test whether muscles reduced femoral deformation and strain during mid-stance.It is widely considered that muscles act as tension chords to minimize bending strain in bones (Witzel and Preuschoft, 2005; Lipphaus and Witzel, 2019; Krahl et al., 2020).This promotes the homogenization of bone strain, which, in turn, facilitates the construction of lightweight bone structures (Witzel and Preuschoft,2005).Furthermore, Duda et al.(1997) proposed that muscles play a substantial role in balancing loads within the femur, encouraging axial loading rather than bending.Lutz et al.(2016) have calculated muscle forces of a human femur by minimization of bending strain, and their results have been validated using finite element simulation, electromyography, and hip reaction force calculation.Additionally, beyond human studies, Shahar et al.(2003) found that the canine femur exhibited slight bending under physiological loads compared to joint load alone.Hence, we expect that muscle forces may reduce the deformation and strain of Cabot’s Tragopan femur during mid-stance.

Thirdly, we test the hypothesis that the M.iliotrochantericus caudalis (ITC) has a significant effect in reducing femoral torsional deformation during mid-stance.In birds, the femur experiences lateral rotation due to knee loading during terrestrial locomotion.This rotation results from both bipedalism and the sub-horizontal orientation of the femur (Carrano, 1998; Carrano and Biewener, 1999; Hutchinson and Gatesy, 2000), and is closely related to their flight adaptation.As theropods evolved along the lineage leading to birds, their enhanced flight capabilities coincided with a shift in femur position towards a more horizontally oriented posture, giving their hindlimbs a crouch posture(Carrano, 1998, 2000; Hutchinson and Gatesy, 2000).Besides, bipeds must position the supporting foot near the sagittal midline to stabilize the body during the single support phase of a gait, and the supporting leg is thus adducted by the vertically-oriented ground reaction force(Gatesy, 1990; Hutchinson and Gatesy, 2000; Allen et al., 2021).Given the sub-horizontal orientation of the femur, this adduction moment leads to the lateral rotation of the femur.Because the femur is sub-horizontally oriented, the adduction moment will rotate it laterally.Throughout theropod evolution, as their femora became more horizontally oriented, the lateral rotation moment acting on the femur increased accordingly (Hutchinson and Gatesy, 2000; Hutchinson and Allen, 2009; Allen et al., 2021).To counteract the increasing lateral rotation of their femora, theropods underwent various modifications in osteology, myology, and neural control (Hutchinson and Gatesy, 2000;Allen et al., 2021).Allen et al.(2021) discovered that, during the evolution of the bird-line, the combined medial rotator moment arms of the hindlimb muscles increased by 146%, with the ITC contributing the most among all muscles.Additionally, extant birds’ ITC exhibits high contraction force during mid-stance (Goetz et al., 2008; Rankin et al.,2016).Consequently, when considering muscle force, ITC appears to have an even more substantial role in resisting femur rotation than previously estimated.We therefore predict that ITC may play a central role in reducing femoral torsion.

2.Materials and methods

2.1.Animals

A total of three adult Cabot’s Tragopans were acquired from the Tragopan Breeding Centre of Beijing Normal University.They were numbered A1 (body mass =1469 g), A2 (body mass =1141 g), and A3(body mass =871 g).The birds all died of natural causes that were not related to musculoskeletal pathology or nutritional deficits, and could not affect the size of muscles and the biomechanical properties of bones.Muscles of the birds were exposed and dissected by Wang et al.(2021).Bones were then soaked in normal saline solution and frozen at -20◦C to keep its physical properties constant (Pelker et al., 1983).

2.2.Inverse simulation for calculating muscle forces

2.2.1.Protocol for solving muscle forces

In this study, we employed inverse simulation to estimate the forces exerted by femoral muscles (i.e., muscles attached to the femur) at midstance during terrestrial locomotion.To achieve equilibrium, the forces generated by these muscles must counterbalance joint loads.Hence,muscle forces were determined by resolving the equations that govern their equilibrium (Shahar and Banks-Sills, 2002).To solve this statically indeterminate problem, we introduced a static optimization technique that minimizes a given performance criterion in the inverse simulation.Consequently, the calculation of muscle forces can be represented by a nonlinear objective function; the general form is:

minf(x)

wherexirepresents the unknown variable to be solved, and in the present study, the muscle force (Fm) is considered as the unknown.Aeqiand beqiare the coefficients of the equality equation (i.e., the equilibrium equation).The lower boundary (lbi) is set to zero to assurexito be positive.The upper boundary (ubi) is determined by 30 N/cm2times the PCSA (physiological cross-sectional area) of each muscle (Close, 1972).The term minf(x) is the performance criterion; minimising the sum of muscle stresses cubed is adopted in the present study (Erdemir et al.,2007).This term can be expressed as:

The equality equation is established such that the sum of the moments generated by muscle forces and the moment of the knee load balance each other at the femoral head.Because the hip joint is a balland-socket joint, the moment from the acetabulum to the femoral head is ignored (Shahar and Banks-Sills, 2002; Bishop et al., 2018).The equilibrium equation is:

whereMmiis the moment of each muscle force to the femoral head andMkis the moment of the knee load to the femoral head.Because the knee load consists of a knee force and knee couple,Mkconsists of the knee force moment (Mk1) and the knee couple (Mk2).The moment equals the force multiplied by the moment arm, and Equation (3) thus can be expressed as:

Fmof each muscle is the parameter to be solved.To solve Equation(5), PCSA,Lm,Fk1,Lk1, andMk2need to be determined in advance.

2.2.2.Muscle measurements and architectural quantification

The insertion and origin sites and PCSA of each muscle were determined through muscle anatomy experiments by Wang et al.(2021).In Wang et al.(2021), the hindlimb muscles of the three adult Cabot’s Tragopans were dissected in detail; the anatomical data for our study were either obtained or derived from their findings.Our study focused solely on muscles directly attached to the femur, and therefore, 21 muscles were picked (see Table 1 for details and muscle abbreviations).Out of these, 13 muscles originate from the femur, while the remaining eight insert into it (Table 1).The origin and insertion sites of each muscle were considered as the points of action for muscle force, with the line between the origin and insertion representing the action line of the muscle force.Certain muscles, such as the M.iliotibialis lateralis and M.iliofibularis, which do not attach to the femur, do not directly influence the stress and strain of the femur.Consequently, the forces exerted by these muscles are not incorporated into our calculations.

The mass and fascicle length of each muscle were obtained from Wang et al.(2021).The muscle volume was calculated by dividing muscle mass by density (1.06 g/cm3) (Mendez and Keys, 1960).Then,the PCSA was calculated by dividing muscle volume by fascicle length.

2.2.3.Establish and solve equilibrium equations

According to published electromyography data for living birds(Gatesy, 1999; Marsh et al., 2004; Cuff et al., 2019) and the setting of Bishop et al.(2018), ITCR and OL were set to be inactive at the stance phase; they were excluded from the calculation.OM, IFE, and IFI were also ignored due to their extremely small size.FPD2, FPD3-M, and FPD4 originate from similar sites and share a similar angle of orientation.The three muscles were thus consolidated into a single entity in the calculation, referred to as the other flexor digit (ODF).Eventually, a total of 14 muscle forces were contained in our equilibrium equations.

To establish the equilibrium,Lm,Fk1,Lk1, andMk2should be determined.Since there is no data available on knee load in Cabot’s Tragopan, we estimate theFk1andMk2of tragopans based on the knee load of chickens (Bishop et al., 2018) and the weight ratio between the two birds.LmandLk1are moment arms of the muscle force and knee force,respectively.Their values were determined by the posture of the femur and the action line of forces.According to Bishop et al.(2018), the general mid-stance posture of ground-dwelling birds is as follows: hip extension of -30◦below horizontal, hip abducted 5◦from midline, hip rotated 20◦externally, knee flexed 93◦from neutral position, ankle flexed 46◦from neutral position, metatarsophalangeal joint extended 16◦from neutral position.

For this study, the hindlimb skeletons of three tragopans were positioned to mimic the mid-stance posture, and photographs were captured from dorsal, lateral, and cranial perspectives using a digital single-lens reflex camera (Nikon D7100) (Fig.1).A right-handed,orthogonal, anatomically based coordinate system was established(Fig.1): the centre of the femoral head was set as the origin of the coordinate system, thex-axis directed caudally, they-axis dorsally, and thez-axis laterally.

The origin and insertion sites of each muscle were located on each skeleton image, guided by the anatomical data from Zhang and Zheng(1996) and Wang et al.(2021).Each pair of sites were connected with straight lines to represent the action line of muscle force (Fig.1).The vertical distance between the action line and the center of the femoral head was measured, providing the moment arm of the muscle force,LmSimilarly,Lk1was determined by measuring the vertical distance between the action line ofFkand the femoral head.

Once the PCSA,Lm,Fk1,Lk1, andMk2have all been determined through the previously described process, the only unknowns in the equilibrium equations are the muscle forces.At this point, the ‘interiorpoint’ algorithm from the Optimization Toolbox of MATLAB (v.R2018a,The Math-Works, Inc.) was used to solve Equation (5), which represents the equilibrium equations, and consequently, the muscle forces are obtained.The muscle moments were then calculated by multiplyingFmbyLmto enable comparisons between individuals of different size, muscle forces and moments were converted to dimensionless quantities.The unit of muscle forces is N, they were thus normalized by dividing by the individual’s body weight (it is calculated by multiplying the body mass by the acceleration of gravity).The unit of muscle moments is Nm, and they were normalized by dividing by the product of body weight and femur length (Jepsen et al., 2015).

2.3.Finite element analysis for estimating femoral strain and deformation

A previously published anatomically accurate, three-dimensional finite element model of the femur of A2 was used (Wei and Zhang,2021).The A2 was chosen because his weight was median among the three individuals.The model was meshed with 10-noded tetrahedral finite elements (C3D10) using an advancing-front algorithm.The element nominal size for the model was 0.4 mm, and the model was meshed into 354,864 elements.The setting of the material properties of the model followed Wei and Zhang’s (2021) method, that is, the elastic modulus of each part is set according to the density distribution of the bone.The model is solid inside, but the regions of very low density(lower than 0.01 g/cm3) were treated as interspaces with in the tissue,and their elastic modulus was set to 0.0001 Mpa to simulate the marrow cavity (Crawford et al., 2003).The hip joint was modelled as a ball-and-socket joint (Bishop et al., 2018); all three translational degrees of freedom of femoral head were restricted while rotational degrees of freedom are unrestricted.Three different loading conditions were simulated independently: 1) case-phys: physiological load, i.e., the femur is loaded by all the muscular and joint loads (Fig.2), to estimate the femoral strain during locomotion; 2) case-eITC: the femur is loaded by all muscle and joint loads except ITC.ITC is the largest muscle attached to the proximal femur of Cabot’s Tragopan (Wang et al., 2021),and it may play an important role in preventing femoral torsion, which is closely related to the adaptation of birds to flight (Allen et al., 2021).Case-eITC aims to reveal the effect of ITC on femoral strain to further clarify the function of this muscle; and 3) case-knee: all muscle forces are removed from the model, and the femur was only loaded by knee loads to reveal their effect on the femoral strain.

The muscle and knee loads were applied to the model in the following manner: The attachment area of each muscle and the action area of knee load were selected on the femur model according to the anatomical experiment records.Then the centre point of the area was determined and the coupling relationship between the centre point and the attachment area was defined in the ABAQUS software (v.2018,Simulia, Dassault Syst`emes).Each load was applied on the corresponding centre point.This approach allows the load to act evenly on the attachment area, which is closer to the actual effect of muscle and joint loads.

For all simulations, the maximum principal strain and minimum principal strain within the femoral models were calculated.The two parameters are measurements of the degree of tensile and compressive deformation, respectively (Goodno and Gere, 2018; Wei and Zhang,2021).Strain is a good predictor of fracture risk and can be used to assess the safety of bone locomotion.It operates under the assumption that higher strain levels indicate a more significant risk condition (Currey,2002; Ulivieri and Rinaudo, 2021).

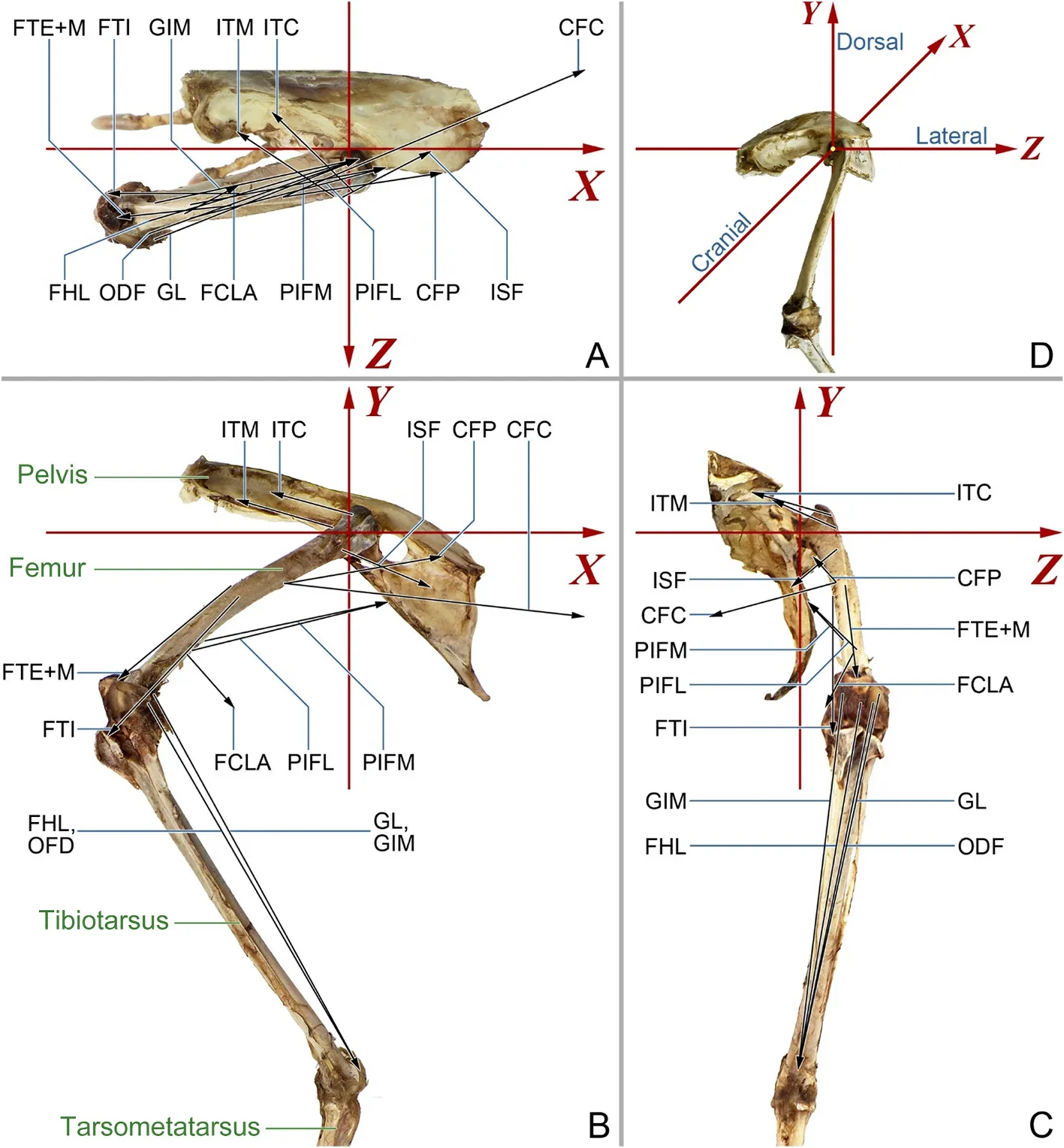
Fig.1.Left hindlimb skeleton and force lines of femoral muscles in Cabot’s Tragopan.(A) Dorsal view; (B) Lateral view; (C) Cranial view; (D) Overview of the coordinate system.The red arrow lines indicate the coordinate system of the hindlimb, with the origin located at the center of the femoral head.Thex-axis points caudally, they-axis points dorsally, and thez-axis points laterally.The black arrow lines represent the femoral muscles, and arrows indicates the direction of muscle forces on the femur.Green texts in (A) indicate skeleton elements.Muscle abbreviations are listed in Table 1.

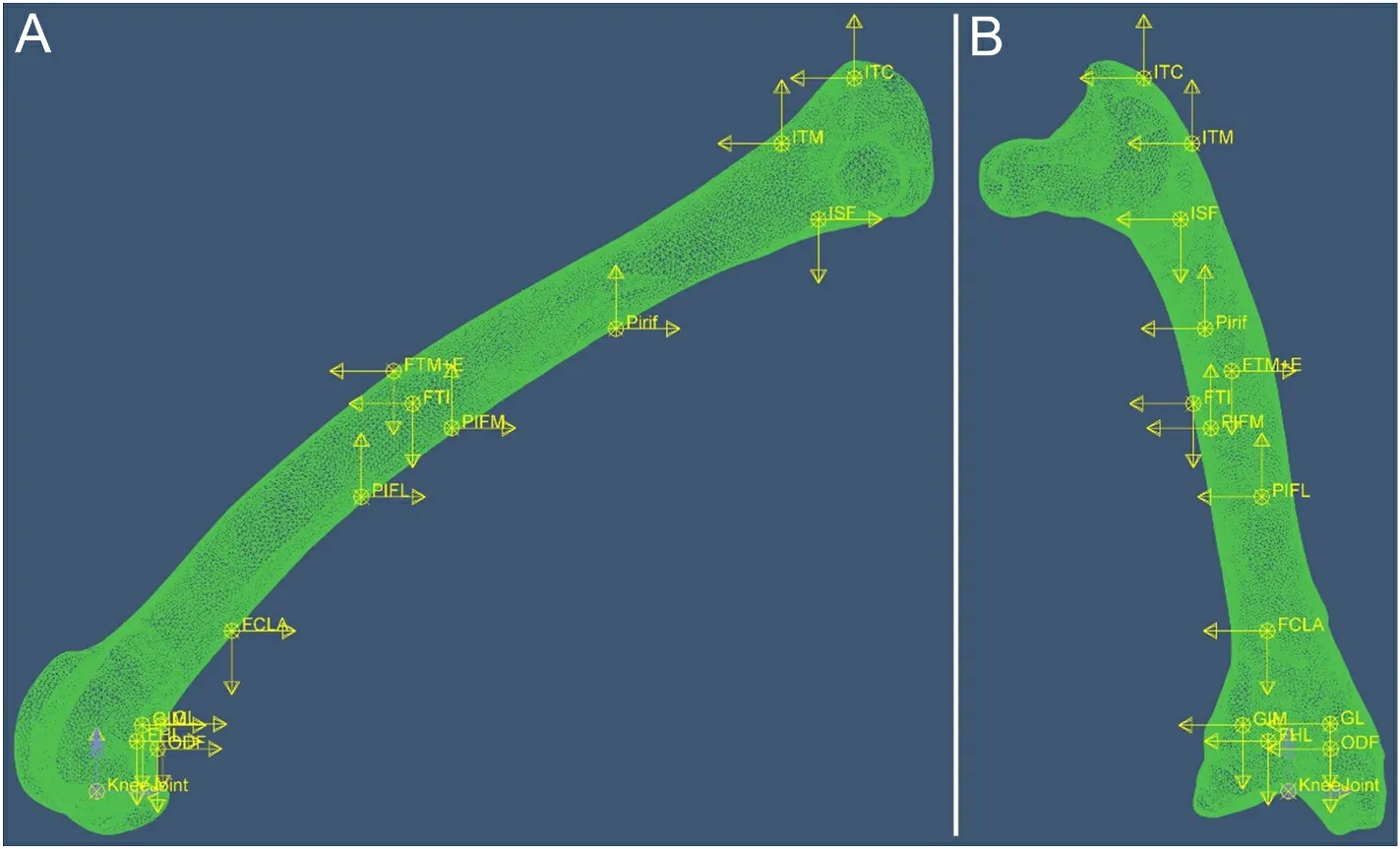
Fig.2.Finite element model of the femur with muscle and knee loads applied.(A) Lateral side of the femur; (B) Cranial side of the femur.Each muscle force is expressed as three components along three orthogonal directions in ABAQUS, represented by yellow arrows in the figure.Blue arrows are knee couples.Arrows indicate the direction of loads; their lengths are not to scale with actual load values.See Table 1 for muscle abbreviations.

3.Results

3.1.Muscle force at the mid-stance

Fig.3A shows the normalized muscle forces during mid-stance.Muscle forces across the three Cabot’s Tragopans display remarkable similarity.Notably, the forces of the ITC (2.59 ±0.10), FTE + M (2.31± 0.25), FCLA (1.07 ± 0.19), and ODF (0.96 ± 0.33) stand out as considerably high.Among these, only the ITC is attached to the proximal femur.

3.2.Muscle moment to the hip joint

Each muscle force has three projections (Fxy,Fyz, andFxz) in theXY,YZ, andXZplanes of the coordinate system, respectively.The moments produced byFxy,Fyz, andFxzon the femur are denoted asMZ,MX, andMY, respectively, and they cause the femur to rotate about theZ-,X-, andY-axes, respectively.

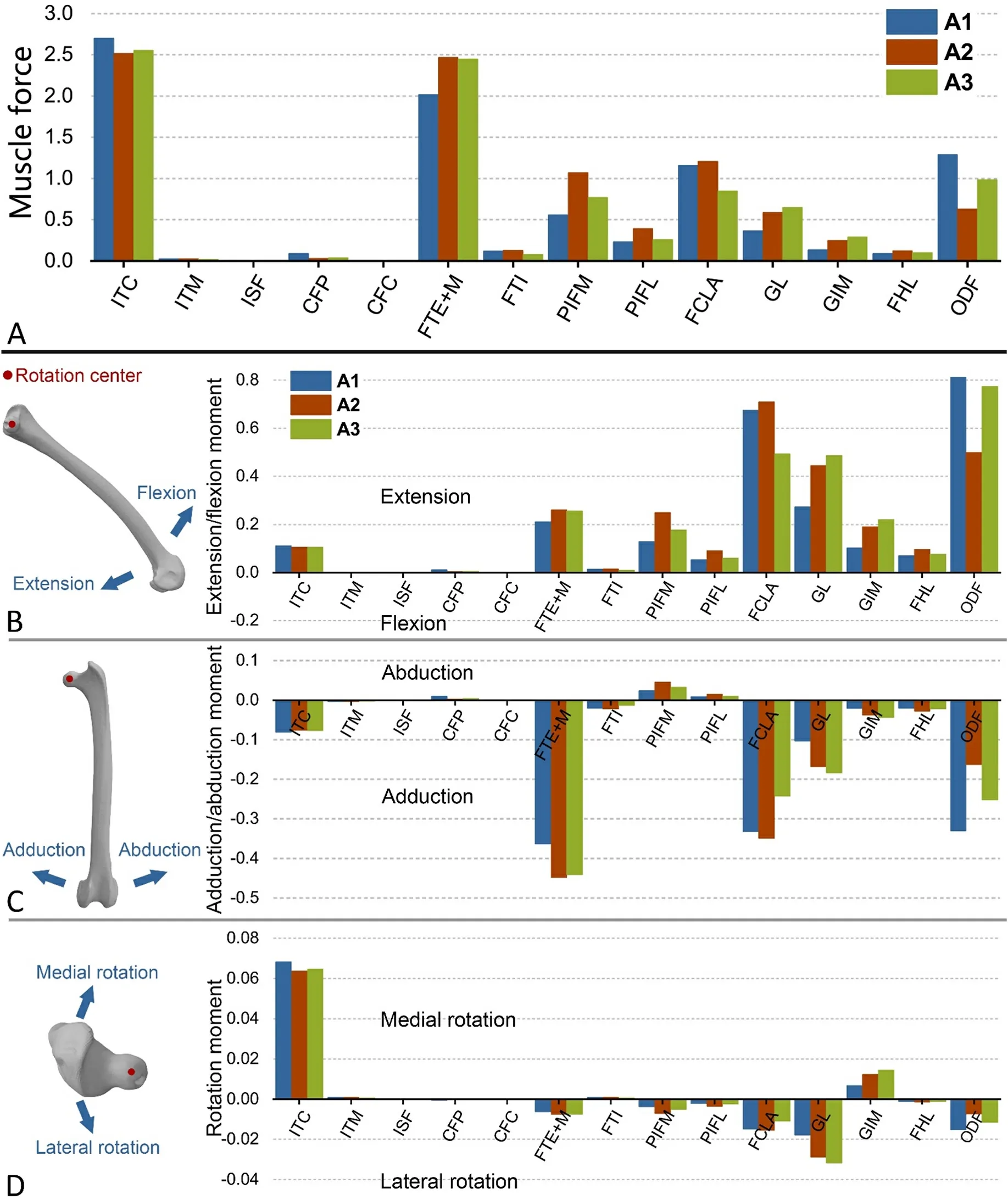
Fig.3.Normalized muscle forces and normalized muscle moments for hip motion.(A) Normalized muscle forces; (B–D) Normalized muscle moments of flexion/extension (MZ), abduction/adduction (MC), and rotation for hip motion (MR), respectively.Femora in B, C, and D are shown from medial, dorsal, and top sides,respectively.See Table 1 for the muscle abbreviations.

MZcauses the femur to rotate about theZ-axis, resulting in hip flexion or extension.MZof each muscle is shown in Fig.3B.The summed muscle moments act as the hip extensor at the mid-stance.Only the ITM is a hip flexor, and its moment is extremely low.FCLA, GL, and ODF have the highest moment of hip extension, followed by FTE +M and GIM.

In the established coordinate system, rotation of the femur about theX- andY-axes causes the thigh to move towards or away from the body.Therefore, bothMXandMYcontribute to hip abduction or adduction,and we therefore addMXandMYto compute the resultant momentMC.Results ofMCshow that muscles generally adduct the femur during midstance (Fig.3C).FCLA, FTE +M, GL, and ODF are strong hip adductors,whileMCvalues of other muscles are extremely low.

Additionally, the component of muscle force (FR) perpendicular to the longitudinal axis of the femur produces a rotational moment (MR),which causes the femur to rotate about its longitudinal axis.The moments produced by each muscle are shown below (Fig.3D).MRof each muscle was calculated by multiplyingFRby the femoral radius at the site of muscle attachment.As shown in Fig.3D, four out of 13 muscles cause the hip to rotate medially.Among them, ITC has the highest moment,followed by GIM.Nine muscles rotate the hip laterally, of which the GL,FCLA and ODF have high moments.

3.3.Finite element analysis

In case-phys, the distal femur shifted ventrally and rotated laterally(Fig.4), indicating that it underwent bending along the dorso-ventral orientation and twisting laterally due to physiological loads.Both the maximum and minimum principal strains were high at the proximal and distal femur (Fig.5A–D), suggesting that these two regions mainly suffered from shear or torsional deformations.In the femoral diaphysis,most areas exhibited high minimum principal strain, with only the lateral side showing a higher maximum principal strain (Fig.5A).This suggests that compression dominates the deformation of the diaphysis,with low bending deformation.Hence, our first hypothesis, that the femur experiences combined deformation during mid-stance, was supported.

Fig.4.Deformation of the femur in three load cases.(A) Distal femur from the bottom view; (B) Whole femur from lateral and dorsal views; (C) Proximal femur from the top view.Meshed and smooth models indicate unload and load scenarios, respectively.To enhance visibility, the femur deformation in the figure has been scaled up by a factor of 5 for load cases 1 and 2, and scaled down to 0.3 times the original deformation for case-knee.

In case-eITC, the femur was loaded by all muscle and joint loads except the ITC.The results show that the femur experiences a greater degree of twist compared to case-phys (Fig.4).However, the strain distribution in the femur is very similar to that of case-phys, except in the proximal part (Fig.5E and F).This indicates that the removal of the ITC has a significant effect on the deformation of the proximal femur.The maximum and minimum principal strains were measured for all the elements (containing 33,572 nodes) on the surface of the femoral neck,and their averages were calculated.In case-phys, the maximum and minimum principal strains of the femoral neck were 2.46 × 10-3and-3.36 × 10-3, respectively.In case-eITC, they were 4.95 × 10-3and-5.60 × 10-3, respectively.Excluding the ITC resulted in a 2.01-fold maximum strain in case-eITC and a 1.67-fold increase in minimum strain compared to case-phys.The results indicate that ITC significantly reduced strain in the proximal femur rather than the entire femur, thus providing partial support for our third hypothesis.

When the femur is only loaded by knee loads (case-knee), there are high minimum and maximum principal strains on the dorsal and ventral sides of the femur, respectively (Figs.4 and 5).The strain values are significantly higher than those in case-phys, the maximum and minimum principal strains of the femoral neck were 6.68 ×10-2and -7.38× 10-2, respectively.The results showed that the femur is predominantly bent along the ventral-dorsal orientation in case-knee, and it experiences more deformation compared to case-phys.It demonstrates that muscle forces can mitigate femoral deformation and strain under physiological loads, thereby supporting our second hypothesis.

4.Discussion

In the present study, we computed the forces exerted by the femoral muscles of Cabot’s Tragopan during the mid-stance phase of terrestrial locomotion using inverse simulation.Subsequently, we determined the moments generated by each femoral muscle on the femur.Utilizing these calculations, we developed a finite element model that accurately represents the femur’s loading conditions during mid-stance, allowing us to measure both maximum and minimum principal strains of the femur.

Combined deformation occurred in femur during locomotion, which mainly involves bending, torsion and compression, supporting our first hypothesis.The results align with the in vivo bone strain data observed in emu femora (Main and Biewener, 2007) and several birds’ tibiotarsus(Biewener et al., 1986; Main and Biewener, 2004, 2006).The complex deformation reflects the intricate loading environment of long bones,which may impede the comprehension of the bone’s form-function relationship.A notable example is the relationship between the cross-section shape of long bones and their habitual loads in locomotion.Several studies have revealed that the orientation of maximum bending rigidity in the cross-section of mammalian and avian long bones does not consistently align with the orientation of habitual bending loads experienced by the bones (Cubo and Casinos, 1998; Demes et al., 2001;Lieberman et al., 2004).Another example is that the cross-sectional structure of hindlimb bones does not allow for the distinction between birds and non-avian theropods, despite their different hindlimb postures during terrestrial locomotion, which result in varying angles of the femur relative to the ground reaction force (Farke and Alicea, 2009).These studies solely considered bending loads when exploring the form-function relationships.As our results show, bones are subjected to combined loads during locomotion, and their form can be influenced by multiple loads.The relationship between bone cross-section shape and specific mechanical requirements can become obscured.A thorough understanding of the bone’s loading environment is imperative to establish a comprehensive form-function relationship of bones.Given the relatively limited research on bone physiological loads in animals,further testing is necessary to collect data that can support more extensive analysis.

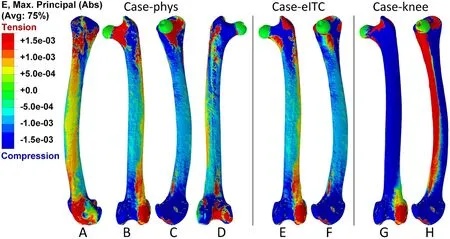
Fig.5.Contour profiles of maximum principal strain (Abs) of the femur in three load cases.(A–D) Femur strain from lateral, dorsal, medial, and ventral views,respectively, under physiological loads (case-phys); (E, F) Femur strain from dorsal and medial views, respectively, under physiological loads except ITC (case-eITC);(G, H) Femur strain from dorsal and medial views, respectively, under knee loads (case-knee).E refers to elastic strain.Abs refers to the absolute value; the contour profiles show the strain with the largest absolute value among the three principal strains at each node of the model.Avg refers to averaging threshold; 75% is a default averaging threshold of ABAQUS in calculating node scalars.

The knee load induced dorsal and lateral bending of the femur, along with lateral torsion.Conversely, muscle loads acted antagonistically to the knee load, resulting in ventral and medial bending, as well as medial torsion of the femur.As a result, the bending moment generated by knee loads was effectively counteracted by muscle loads, leading to a substantial reduction in femoral deformation and strain under physiological loads (case-phys).Therefore, our second hypothesis was supported.This characteristic enhances the safety of bones during motion, and may allow birds to meet mechanical requirements with lighter bones.Similar phenomena have long been studied in humans, particularly in the femur.Studies have suggested that muscle loads can balance the bending moment of the femur, reduce femoral strain, and create a more uniform strain distribution (Taylor et al., 1996; Duda et al., 1997, 1998; Rudman et al., 2006; Sverdlova and Witzel, 2010; Lutz et al., 2016).While only a limited number of studies have measured stress and strain on animal bones under physiological loads, similar conclusions have been reached(Shahar et al., 2003; Krahl et al., 2020).Shahar et al.(2003) found that the canine femur exhibited slight bending under physiological loads compared to joint load alone.Furthermore, the stress and strain were significantly reduced when considering both muscle and joint loads.Birds adopt a more crouched hind limb posture compared to humans and canines (Gatesy and Middleton, 1997; Shahar and Banks-Sills, 2002;Allen et al., 2021), resulting in a higher moment exerted on the femur by the ground reaction force.However, even in this scenario, our study demonstrates that muscle forces substantially reduce femur bending in Cabot’s Tragopan.Therefore, the bone deformation reducing function of muscles may be a common trait at least in birds and mammals.

The femoral diaphysis of Cabot’s Tragopan mainly experiences compressive deformation under physiological loading (Fig.5A–D).This phenomenon has also been observed in femora of human and canine(Duda et al., 1997; Shahar et al., 2003; Sverdlova and Witzel, 2010).Bones have higher resistance to compressive load than to tensile and shear loads (Currey, 2002).Their favourable material properties are most effectively utilized in loading environments predominantly characterized by compressive forces.This optimization further enhances the locomotion safety of bones.Sverdlova and Witzel (2010) suggests that this condition may indicate bone adaptation to the specific loads they are subjected to, potentially enabling the musculoskeletal system to form a light-weight mobile structure.Muscle forces can not only decrease bone strain but also influence the type of strain experienced by the bone.Considering the direct relationship between strain and the likelihood of fractures, this muscle function showcases its capability to optimize the skeletal loading environment.Furthermore, such phenomena can be observed even when focusing on individual muscles.Milne and O’Higgins (2012) found that in xenarthran, gluteus maximus and tensor fasciae latae, attached to the third trochanter of the femur,can reduce the bending deformation of the femur.These conclusions suggest that the effect of muscle on skeletal load should also be considered in functional studies of muscles.Furthermore, it is necessary to approach musculoskeletal research in an integrated manner, considering the entire system.

Our third hypothesis that ITC has a significant effect in reducing femoral torsional deformation during mid-stance was partial supported by our results.The knee couple (MK2) rotates the femur laterally during mid-stance.However, our findings reveal that only the ITC produces a substantial medial rotation moment to counteract femur rotation.The rotational moments generated by other muscles appear to be relatively low, with the most of the femora muscles even contributing to lateral femur rotation (Fig.3D).ITC can only reduce the torsional deformation in the area to which it is attached, i.e., the proximal femur.Besides, the FEA results unambiguously demonstrate that when the ITC muscle force is excluded (case-eITC), the femoral neck undergoes more pronounced twisting, and the strain significantly increases, but no obvious change in other regions.Since the cortical bone at the femoral neck is thin, it is more susceptible to fractures and inherently vulnerable (Ford et al.,1996; Abe et al., 2016).We hypothesize that the substantial rotation moment generated by the ITC serves to protect the femoral neck.As the femoral head extends beyond the diaphysis, the femoral neck experiences shearing forces between the acetabulum and diaphysis during femur rotation.It results in stress concentration on the femoral neck,increasing the risk of fractures.The medial rotation moment provided by the ITC can counterbalance or mitigate the lateral rotation moment on the proximal femur, consequently protecting the femoral neck from fractures.Other sections of the femur may possess adequate strength to withstand rotational moments, and the diaphysis is relatively smooth and lacks structures that cause the stress concentration.This could explain the low rotational moments observed in most femoral muscles.

As mentioned in the introduction, the lateral torsion of the femur of birds is related to their adaptation to flight.During the evolution of theropods to birds, the torsion moment on the femur increased with the development of their flight ability.ITC plays a crucial role in counteracting the increasing lateral rotation of their femora.In ancestral archosaurs, M.iliofemoralis (IF) (homologue of the dinosauromorph/avian ITC) is active at the swing phase, and it acts as a hip abductor during locomotion (crocodiles still retain this trait) (Hutchinson and Gatesy, 2000; Reilly and Blob, 2003).Throughout the evolution of theropods, IF/ITC activity shifted from the swing phase to the stance phase, with its primary function changing from abduction to medial rotation (Hutchinson and Gatesy, 2000).Allen et al.(2021) reported a remarkable 146% increase in the combined medial rotator moment arms of hindlimb muscles during the evolution of the bird-line, signifying a substantial enhancement in resistance to femur lateral rotation.Notably,ITC contributed significantly to this increase, accounting for 45% of the total increment, the highest among all muscles.Moreover, if we exclude muscles that are inactive during the stance phase [i.e., M.iliotibialis cranialis (IC), ITCR, and OM], as well as smaller-sized muscles (i.e., IFI and IFE), the ITC moment arm alone constitutes 82% of the total increase.In addition, as observed in our study and supported by previous research (Goetz et al., 2008; Rankin et al., 2016), ITC exerted substantial contraction force during mid-stance.This observation indicates that ITC plays an even more significant role in resisting femur rotation than previously estimated.Our findings align with this assumption, as we found that ITC has the highest medial rotation moment among the femoral muscles of Cabot’s Tragopan and a significant impact on reducing strain on the femoral neck.

ITC mainly reduced the deformation of the proximal femur instead of the whole femur, suggesting that the proximal femur may be particularly influenced by alterations in the femoral loading environment during the evolution of flight.As previously mentioned, ITC functions as a medial rotator of the hip, which helps protect the vulnerable femoral neck from fractures.The evolutionary changes in ITC may also due to the protection to the femoral neck.Since theropods adept at flight experience high proximal femur rotation during bipedal locomotion, resistance to lateral rotation of the proximal femur could potentially serve as an indicator of the hindlimb posture adopted by bipeds in terrestrial locomotion, and subsequently, their flight capabilities.This offers another perspective for studying the origin of bird flight.Allen et al.(2021) calculated the changes in the ITC moment arm of bird-line archosaurs during evolution.Future research should investigate the muscle force of the ITC to calculate muscle moments more accurately, allowing for a better assessment of the evolutionary changes in theropods’ ability to resist femur rotation.

A limitation of our study should be noted.There have been no studies collecting kinematic and kinetic data for Cabot’s Tragopan.As these birds are a vulnerable species, invasive in vivo tests involving them are not be allowed by law.Consequently, the kinematic data used in our muscle force calculations, such as joint angles, are derived from a generalized mid-stance posture of extant ground-dwelling birds as summarized by Bishop et al.(2018).This may differ from the actual posture of Cabot’s Tragopan.This also raises the question of whether kinetic and kinematic data can be accurately inferred from homologous or analogous species.As the locomotion of extinct species cannot be directly tested, this issue remains a challenge for paleontological research.A study by Meilak et al.(2021) demonstrated that passerines may exhibit similar take-off behaviour, enabling efficient locomotion.This finding suggests that bird locomotion may adhere to certain physical principles and offers insights for reconstructing the locomotion of extinct species.Furthermore, in the context of that the long bone’s mechanical performance of birds (or even most animals) in locomotion has not been explored in detail, the purpose of this study is to explore the general pattern of the femora deformation and strain of ground-dwelling birds more than to get accurate results for Cabot’s Tragopans specifically.The use of Bishop et al.(2018)’s data in our experiments has a limited impact on our conclusions.Besides, Cabot’s Tragopan is more arboreal than other pheasants.It may have the muscle activity pattern different to species of more ground-dwelling lifestyle.However, due to the lack of data for comparison, this hypothesis needs to be explored by further research.

5.Conclusions

Cabot’s Tragopan’s femur underwent combined loadings and deformed in a combination of bending, compression, and torsion during mid-stance.The complex loading environment of bones complicates the study of the form-function relationship.The actual physiological loads experienced by bones during locomotion should be fully considered to ensure that the conclusions are credible.Muscle forces reduced the strain/deformation of bones during locomotion, and make the femur loaded mainly in the form of compression.The trait improved the locomotor safety of femora, and allowed the bones to meet mechanical requirements with a lighter weight.It also highlights the close connection between muscles and bones.Muscles and bones work together as a cohesive unit during locomotion.It reminds us to understand the function of muscles and bones from the perspective of the musculoskeletal system.ITC showed high resistance to femoral torsion that significantly exceeds that of other muscles, which may be an adaption to protect the vulnerable proximal femur (femoral neck).Femur torsion is the result of a combination of the bipedalism and the crouch posture of the hindlimb of birds.Given that the crouched hindlimb posture of birds is closely related to their adaptation to a flight lifestyle, the characteristics of ITC may be an important component in exploring the origin of avian flight.

Funding

This work was supported by the National Natural Science Foundation of China (No.31471951, No.31970411).

Ethics statement

The project was approved by the Animal Care and Ethics Committee of Capital Normal University.

CRediT authorship contribution statement

Xinsen Wei:Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft,Writing – review & editing.Zihui Zhang:Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Writing – original draft, Writing – review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors thank Yanyun Zhang from the College of Life Sciences,Beijing Normal University, for providing bird samples; Qunbo Fan from the School of Materials Science & Engineering, Beijing Institute of Technology, Baoqing Pei from the School of Biological Science and Medical Engineering, Beihang University, Yangwei Wang and Tao Sun for technical support; Peter Bishop from Museum of Comparative Zoology, Harvard University, for providing detail kinetic data on birds.Maja Mielke and an anonymous reviewer for constructive comments that improved the study.