一种面向低成本轻量级雷达的单比特复用阵列信号收发框架
冯力方 黄 磊 周汉飞 李 强 刘仕奇 张沛昌
①(深圳大学电子与信息工程学院 深圳 518060)
②(深圳大学射频异质异构集成全国重点实验室 深圳 518060)
1 引言
随着小载荷无人机频繁运用于军事活动,寻求低成本轻量化的雷达系统以满足稳定获取目标的应用需求日益迫切。特别是,在保证探测性能的前提下,如何降低数字阵列雷达的成本、能耗与重量,一直是雷达领域的研究热点。
数字阵列雷达,通过将每个天线阵元信号进行数字化收发,获得了极大的信号处理自由度,是一种理想的雷达方案。然而,其高昂的成本、较大的能耗与重量,通常让其难以在小载荷无人机中得到应用。根据雷达组成原理,发射机与接收机是数字阵列雷达系统主要的成本与重量来源之一。因此,如何在保证雷达性能的前提下,减少发射机与接收机的数量是实现低成本轻量级雷达设计的关键难题之一。
稀疏阵列[1,2]与稀布阵列[3]的优化设计技术可以删除阵列雷达中的冗余通道,从而达到降低成本与重量的目的。但是,为了保证雷达波束的低旁瓣特性,其删减通道的数量也极为有限。并且,剩余的每个收发阵元需配置独立的发射/接收机,使得系统的成本与重量仍然居高不下。基于子阵结构的阵列优化技术[4]可以让多个阵元共享同一个接收机,但会降低空域维的信号处理自由度[5],从而影响了雷达的探测性能。互质阵[6]与嵌套阵[7]技术可以采用较少的接收通道,合成较大孔径的等效阵列,然而每个接收阵元也需配置独立的接收机。时分复用-多输入多输出(Time Division Multiplexing -Multiple Input Multiple Output,TDM-MIMO)技术[8,9]可以减少发射机的数量,缩小阵列天线的实孔径,但每个接收阵元仍需配置独立的接收机;在TDM-MIMO的基础上,文献[10]对发射信号的相位进行调节,实现了虚拟孔径的扩展,从而减少了收发通道,但该技术只能在较小的角度范围内提高角度分辨,其应用场景常常受到限制。文献[11]利用多个阵元时分复用同一个通道的形式来减少接收机的数量,然而其复用次数常常受到模数转换器(Analog-to-Digital Converter,ADC)采样速率与成本的限制。
近年来,随着单比特采样量化技术的发展,出现了大量关于单比特信号处理的研究,例如,单比特量化器设计[12],单比特信号检测[13-19],单比特正弦参数估计[20,21],单比特到达角(Direction of Arrival,DOA)估计[22-24],单比特波束形成[25],单比特压缩感知[26,27]等。伴随上述研究,也出现了许多基于单比特采样量化的雷达系统,例如,单通道的单比特雷达[28-30],单比特线性调频连续波(Linear Frequency Modulation Continuous Wave,LFMCW)阵列雷达[31],单比特共置MIMO雷达[32-36],单比特分布式MIMO雷达[37]和单比特合成孔径雷达[38-41]等。总的来说,上述研究旨在利用单比特采样量化来降低数据量和系统载荷,并在匹配滤波时提升信号处理的计算效率,从而达到降低系统成本的目的。然而,在面向小载荷无人机雷达的应用时,单纯的通过置换单比特ADC的途径,对数字阵列雷达低成本轻量化设计的贡献十分有限。
基于上述的研究现状及其存在的问题,本文提出了一种联合单比特采样量化和接收机复用的阵列雷达信号收发框架,以满足低成本轻量级雷达的应用需求。本文主要创新点如下:
(1) 针对低成本轻量级雷达的应用需求,利用单比特采样的高速特性和接收机复用的低成本特点,构建了一种基于单比特复用阵列 (Single-bit Multiplexing Array,SMA)的LFMCW信号收发框架。通过介绍SMA的工作原理,并将其运用于TDMMIMO,阐述了该框架在节省接收机数量方面的优势。更重要的是,本文从雷达资源配置的角度,分析了单比特采样量化在SMA中的重要性,以及SMA可以利用时间换空间获得比经典LFMCW雷达更好的探测性能。
(2) 推导了基于SMA框架的雷达测距、测速和测角公式,以及目标参数估计的克拉美罗界(Cramér-Rao Bound,CRB)。通过对CRB的仿真,验证了SMA利用时间换空间带来更好探测性能的理论。同时,分析了多目标探测场景中,强目标对弱目标的影响,并给出了多目标稳定探测的信噪比(Signal to Noise Ratio,SNR)条件。
(3) 将单比特多重信号分类(Multiple Signal Classification,MUSIC)算法[24]推广为单比特2DMUSIC算法,并利用一种基于单比特2D-MUSIC的速度维配对算法,验证了SMA雷达获取目标原理的正确性,以及采用CRB对SMA进行分析的可靠性。
为了避免词汇概念的混淆,在本文中,采样指的是对连续时间信号在时间上进行离散化,其离散化的频率即为采样频率;量化是指将采样得到模拟域中的数值映射到一个离散数值集合的过程;采样与量化实现的工具为ADC。由于ADC的最高采样频率受量化位数的限制,通常量化位数越低,其最高采样频率越高。因此本文约定:当涉及单比特ADC的高速采样特性时,采用术语“单比特采样”;当只涉及数值映射时,采用术语“单比特量化”;当涉及以上两种情况时,采用术语“单比特量化采样”;当涉及采样与量化的实现工具时,采用术语“单比特ADC”。
2 系统模型
2.1 SMA框架的基本组成
本文以线性阵列为例,提出了一种基于SMA的FMCW雷达信号收发框架,其原理框图如图1所示。该框架通过发射机与天线阵元向外辐射LFMCW信号,同时利用接收阵元接收目标反射的回波信号,并通过时分复用的方式将多个接收阵元的信号接入零中频接收机。随后,阵元信号经过限幅调理、低噪声放大、正交解调和抗混叠滤波之后,将变成I,Q两路信号。最后再将信号送往单比特ADC进行采样量化以及后续的信号处理。

图1 SMA框架示意图Fig.1 The schematic diagram of SMA framework
与传统阵列雷达不同,由于采用了时分复用的方式来接收多个阵元信号,因此SMA雷达仅含1个接收机,也可以实现阵列信号的数字化接收,极大地减少了数字阵列雷达的接收机数量,降低了系统的负荷与成本。同时,SMA采用了单比特采样量化的方式,不但简化了信号的采集方式,其较高的采样速率还可以进一步升提接收机的复用次数,进而提升雷达的性能。接下来,本文利用SMA在TDMMIMO雷达中的应用,来介绍SMA节省接收机数量的特点,然后从雷达资源配置的角度,来分析SMA中单比特采样量化的必要性以及SMA的先进性。
2.2 SMA框架的应用方式
在基于通道复用的阵列雷达中,由于时间资源的限制,单个接收机通常只能复用有限个数的阵元。因此,在实际场景中,可以同时应用多个SMA框架。例如,与TDM-MIMO结合,可以得到SMAMIMO雷达收发框架,如图2所示。发射机以复用方式与多个发射阵元相连接,接收机以复用方式与多个接收子阵列相连接。每个接收机分时接收1个子阵内的多个阵元信号。发射机和接收机的复用过程是协同进行的。接下来,本文将通过一个具体的例子来说明SMA-MIMO信号收发的流程。在该例子中,假设系统有2个发射阵元,分别命名为T1和.T1.;有2个接收子阵,每个子阵列含3个接收阵元,总共6个接收阵元,分别命名为R1-R6.;有1个发射机和2个接收机,每个接收机复用3个阵元。

图2 SMA在TDM-MIMO中应用的示意图Fig.2 Schematic diagram of SMA application in TDM-MIMO
SMA-MIMO天线工作原理如图3所示。首先,其天线的工作时序如图3(a)所示,图中用红色表示发射/接收阵元处于接入状态,用黑色表示未接入状态。发射阵元和接收阵元以循环轮转的方式,分别接入接发射机和接收机。在单个的循环轮转中,可以分6个时刻来描述天线接入状态。从t1至t3时刻,发射机接入发射阵元T1,两个接收机分别依次接入阵元R1,R2,R3和R4,R5,R6。从t4至t6时刻,发射机接入发射阵元T2,接收机接入阵元的方式与t1至t3时刻一致。从t1至t6,发射机重复发射6次相同的LFMCW信号。因此,远场条件下,在一个相参处理间隔(Coherent Processing Interval,CPI)内,各阵元R1-R6接收到回波信号之间的相位差可以被认为由目标的DOA和径向速度、收发阵列的阵列布局以及复用间隔决定。这样,与TDMMIMO天线孔径的等效原理类似,在t1至t6内,6个阵元接收到的信号在经过合理的补偿处理(见第3节) 之后,可以等效为12个阵元接收到的信号,其等效接收阵列如图3(b)所示。假设发射阵元之间的间距为D1,接收阵列实孔径为D2,则等效接收阵列的孔径为D1+D2。

图3 SMA-MIMO天线工作原理Fig.3 Working principle of SMA-MIMO antenna
从上述例子可以看出,SMA-MIMO收发框架仅需要2个接收机就可以实现12个阵元的等效阵列,而传统SIMO数字阵列雷达需要12个接收机,现有最新的TDM-MIMO框架也需要6个接收机,如表1所示。因此,SMA框架可以节省大量的发射机和接收机,从而减轻系统载荷,降低系统成本。另一方面,假如发射机复用更多的发射阵元,每个接收机复用更多的接收阵元,则该框架可以获得阵元更多、孔径更大的等效接收阵列,从而进一步提升雷达的角度分辨率。此外,增加的发射/接收阵元通常都是无源器件,载荷较轻,成本较低。

表1 不同收发框架需要收发机的数量Tab.1 Number of transceivers required for different frameworks
2.3 SMA框架的资源配置
从雷达资源配置的角度上来看,SMA采用多个阵元复用接收机的方案,是一种时间换空间的雷达资源配置策略,即在保持接收机数量不变的前提下,通过开销更多的时间,以复用的方式,来获得更多空间上的阵元数据。然而,雷达的时间资源是极为宝贵的,如何用较少的时间来获取更多的阵元数据是亟待解决的难点问题。在这方面,SMA框架采用了单比特ADC,使得SMA在雷达资源配置方面具有较大优势,主要体现在以下两个方面:
(1) 单比特采样可使SMA雷达更好地实现时间换空间的雷达资源配置策略,理由如下:
基于SMA的雷达发射机和接收机在经过多次复用后,为了保证雷达测量的数据率(即每分钟对雷达覆盖范围探测的次数),通常会缩短雷达信号的脉冲宽度。LFMCW零中频接收机输出差频信号(即I路和Q路信号)的频率正比于Bτ0/T,其中,B为信号宽带,τ0为目标回波延时,T为脉冲宽度。当T成倍数地减少时,差频信号的频率将以相同倍数增加,则相应ADC的最高采样速率也需要成倍数增加。通常ADC的最高采样速率会随着ADC比特位数增加而降低,其成本也会以指数形式增加。因此,传统多比特ADC的采样速率及其成本将会限制发射机与接收机的复用次数。SMA采用单比特ADC恰好可以克服上述采样速率与成本的问题,可以更好地实现利用时间换空间的雷达资源配置策略。
(2) 单比特采样量化可使雷达资源配置更细精、更灵活、更均衡,理由如下:
(a) 在一个CPI内的接收数据中,快时间维、慢时间维、空域维中的数据量分别代表着雷达资源在距离维、速度维、角度维的配置情况。某一维的数据量越大,则表明该维的资源配置占优,测量性能通常较好。经典LFMCW雷达和SMA雷达的数据资源配置情况可以总结在图4中,图中立方体的长、宽、高分别表示了雷达在快时间维、慢时间维和空域维中的数据量。

图4 雷达资源配置对比示意图Fig.4 Schematic diagram of radar resource allocation comparison
(b) 当ADC采样频率保持为最远探测距离对应差频信号频率的2倍时(即最高差频信号所对应的奈奎斯特频率),采用单比特采样和多比特采样在快时间域内获得的采样点数是一致的(因为采样点数是由最远探测距离和距离分辨率决定的)。就单个阵元而言,多比特采样量化得到的数据比特量远大于单比特采样量化。前者相对于后者,在时间维上存在着大量的数据冗余。后者相对于前者,在时间维上损失了部分数据资源。然而,在SMA的框架中,利用复用得到的多个阵元数据,不但可以弥补单个阵元在时间维上数据资源的损失,还可以增加空域维的数据量,克服了传统雷达空域维数据资源不足的缺点,使雷达资源配置更均衡。
(c) 综上所述,SMA雷达利用单比特ADC的高速采样特性,在快时间域获得了更精细的时间碎片,并通过复用的方式,在这些时间中获得了更多的空域维数据资源,弥补了空域资源的不足,同时还删除了时间维中的冗余数据。因此,单比特采样量化在SMA中的应用,可以提高每个比特数据在空域维、快时间维和慢时间维中的利用率,使雷达资源配置更细精、更灵活、更均衡,如图4中红色虚线部分所示。SMA以时间换空间的方式获得更好的雷达探测性能,可以从后面的仿真验证中得到证实。
3 系统估计性能
本节将通过推导雷达目标参数估计的CRB,来进一步验证SMA利用时间换空间所带来的性能优势。为了使本文主题更加聚焦,本节主要以SMA的基本框架(即雷达只含1个发射机、1个发射阵元、1个接收机和多个接收阵元)为对象进行讨论。此外,该框架适用于接收阵元均匀或非均匀排列的线阵或面阵,为了模型描述上的简洁,本文以均匀线性阵列为例进行讨论。
3.1 信号模型
考虑一个具有M个接收阵元的SMA框架,其发射LFMCW信号的时频曲线如图5所示,发射信号的脉冲宽度为Tw,脉冲周期为Tc,信号带宽为B。SMA以循环轮转的方式,将M个阵元分时接入接收机,接入一轮所花的时间为Tr=MTc,Tr也表示SMA雷达信号的脉冲重复周期。图5用不同的颜色区分了各接收阵元,在M个发射周期内分时接入接收机的持续时间。
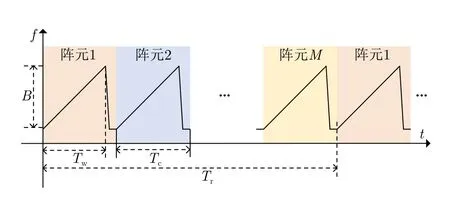
图5 发射信号的时频曲线和接收阵元分时接入的时序Fig.5 Time-frequency curve of the transmitting signal and sequential of the time-division access of receiving elements
根据LFMCW雷达原理[30],该SMA框架接收的零中频信号可以建模为式(1)的形式。
其中,ym(l,p)为第m个阵元接收p个脉冲中第l个采样点的复信号,m=1,2,...,M,p=1,2,...,P,l=1,2,...,L,P和L分别为脉冲个数和单个脉冲周期的采样点数。Ts为ADC的采样周期。αi,γi,βi,δi和φi分别为第i个点目标回波信号的幅度、距离维频率、方位维空间频率、速度维多谱勒频率和初始相位,i=1,2,...,I,I为目标个数。γi=2riB/(Twc),βi=dsin(θi)/λ,δi=2vi/λ。ri,θi和vi分别为第i个点目标的距离、方位和速度。c为光速,d为阵元间距,λ为载波波长。wm为第m个阵元零中频信号中的噪声分量。此外,csign(x)=sign(ℜ(x))+jsign(ℑ(x)),ℜ(·)和ℑ(·)分别表示取实部和取虚部操作,sign(·)为符号函数,对应单比特量化。
此外,每个接收阵元收到的信号可能还会引入由系统误差引起的相位误差,这可以利用实验测量,并通过控制阵元接入时刻来得到补偿。
由于复用接收方式的引入,空间频率βi与多谱勒频率δi也存在着耦合关系。为了处理方便,本文引入3个数字角频率bi,gi和hi,将它们表示为
这样,式(1)可以重新表达为
其中
3.2 CRB推导
当假定各个阵元中噪声分量为功率相同的复高斯噪声时,其噪声功率可以设置为不为0的任意正实数。这是因为在式(1)中,对 csign(x)中的x乘以任意大于0的数,均不会对ym(l,p)产生任何影响。通过将噪声功率参数进行归一化操作,可以将未知的噪声参数合并至αi,此时αi表示第i个目标回波信号信噪比的平方根。这样,待估计的参数可以简化为向量φ=
通过将M个阵元接收采样的零中频信号进行排列,可以得到数据向量y=[y1(1,1),...,y1(L,1),...,y1(L,P),...,yM(L,P)]T∈RLPM。这样,SMA采样数据的似然函数可建模为
其中
待估计参数φ的费希尔矩阵F(φ)可以表示为
其中,式(10)中的数学期望是对p(y|φ)求取的。
对于任意的1 ≤u,z≤LPM,利用ℜ(yu)与ℑ(yz)之间的独立性和正则条件,有
将式(11)代入式(10),经整理可以得到[26]
式(13)中的数学期望是对p(ℜ(yk)|φ)求取的,式(13)中第3个等号是在导数项与ℜ(yk)无关的前提下得到的,其求导运算可以由式(14)-式((21)给出。此外,可以通过将式(1 3)中 的ℜ(sk(φ))替换成ℑ(sk(φ))来获得。
式(23)中雅可比矩阵∂χ(φ)/∂φ由式(24)给定。
其中,Blkdiag(·)为块对角化操作,
3.3 验证分析
本节将利用CRB来验证SMA利用时间换空间所带来的性能优势,并分析了SMA应用的SNR边界条件。
在仿真中,雷达参数按最远探测距离为50 m,最快目标速度为10 m/s进行设置。雷达工作的载波频率77 GHz,射频带宽为100 MHz。为了进行对比,设置了10组雷达案例,如表2所示。TMLR为传统1发1收的、多比特采样的LFMCW雷达(Traditional Multi-bit LFMCW Radar,TMLR)。SMAR为本文所提出的SMA雷达(SMA Radar,SMAR),SLAR表示如文献[31]中不采用复用技术的单比特阵列雷达,即直接用多个单比特ADC分别替代传统LFMCW阵列雷达中多比特的ADC的雷达,为了方便,称之为单比特LFMCW阵列雷达(Single-bit LFMCW Array Radar,SLAR)。案例名中的后缀 -x表示采用了x个阵元。为了对比上的公平,设置雷达信号处理的CPI均为1.2 ms,其脉冲重复周期按照最快目标速度所对应多谱勒频率的2倍来计算,即为97.4026 μs。用总的CPI与脉冲重复周期相除,可以计算出脉冲重复的个数为12个。为了计算上的方便,我们假设脉冲宽度Tw与脉冲周期Tc是相等的。这样可以得到TMLR的脉冲宽度也为97.4026 μs,SMAR随着复用阵元数增加一倍,其脉冲宽度也缩短一半。TMLR采用传统多比特ADC,在计算时采用了无量化的方式。TMLR和SMAR的采样率为最远目标回波的差频信号频率的2倍。快时间域和慢时间域中的采样率均按照奈奎斯特频率来设置,可以使硬件资源的利用率达到最大。在这样的设置原则下,TMLR与SMAR单周期采样点数是相等的,均为66。为了对比复用技术对雷达测角性能的影响,SLAR的参数与SMAR保持一致。此外,设置目标个数为2,其目标参数对(距离,速度,方位角)分别为(22 m,8 m/s,-20°)和(37 m,5 m/s,8°)。此外,我们定义第i个目标的SNR为其中为白噪声功率,在仿真中设置为1,SNR由αi给定。

表2 不同雷达类型的参数Tab.2 Parameters of different radar types
3.3.1 相同SNR目标的估计性能
在本节中,设置两个目标SNR相等,绘制出CRB随SNR变化的曲线如图6-图8所示。

图6 距离估计性能Fig.6 Distance estimation performance
如2.3节所述,在相同的CPI内,SMAR通过合理配置可以获得比TMLR更好的探测精度,实现了利用时间换空间带来探测性能上的增强。特别是针对的微弱目标,SMAR更具优势。从图6和图7可以看出,当阵元数小于等于2时,SMAR由于单比特采样带来单个阵元信号信噪比损失,进而导致测距与测速精度相对TMLR有所下降;当SMAR的阵元数增多时,其测距与测速精度将明显提升。图中当阵元数为4,8,16时,SMAR在目标信噪比小于0 dB时的测距与测速精度明显优于TMLR。

图7 速度估计性能Fig.7 Velocity estimation performance
SMAR采用1个接收机也能获得较高的测角精度。如图8所示,随着阵元数的增多,SMAR的测角精度明显提升。当阵元数大于8时,SMAR几乎可以实现在目标信噪比大于-18 dB条件下1°以内的角度估计误差。这是1发1收的TMLR难以达到的。此外,尽管复用机制的引入使得接收信号模型出现了角度与速度耦合,但SMAR也可以获得与SLAR几乎一致的理想测角精度。此外,由于两目标的SNR一致,因此这两个目标在测距、测速和测角上具有几乎一致的CRB曲线。

图8 DOA估计性能Fig.8 DOA estimation performance
3.3.2 不同SNR目标的估计性能
在本节中,设置第1个目标的SNR为0 dB或为-10 dB,第2个目标的SNR在-20 dB与16 dB之间变化。绘制出CRB随第2个目标SNR变化的曲线如图9-图11所示。图例中后缀名-1st与-2nd分别表示第1个目标的探测精度与第2个目标的测探精度。
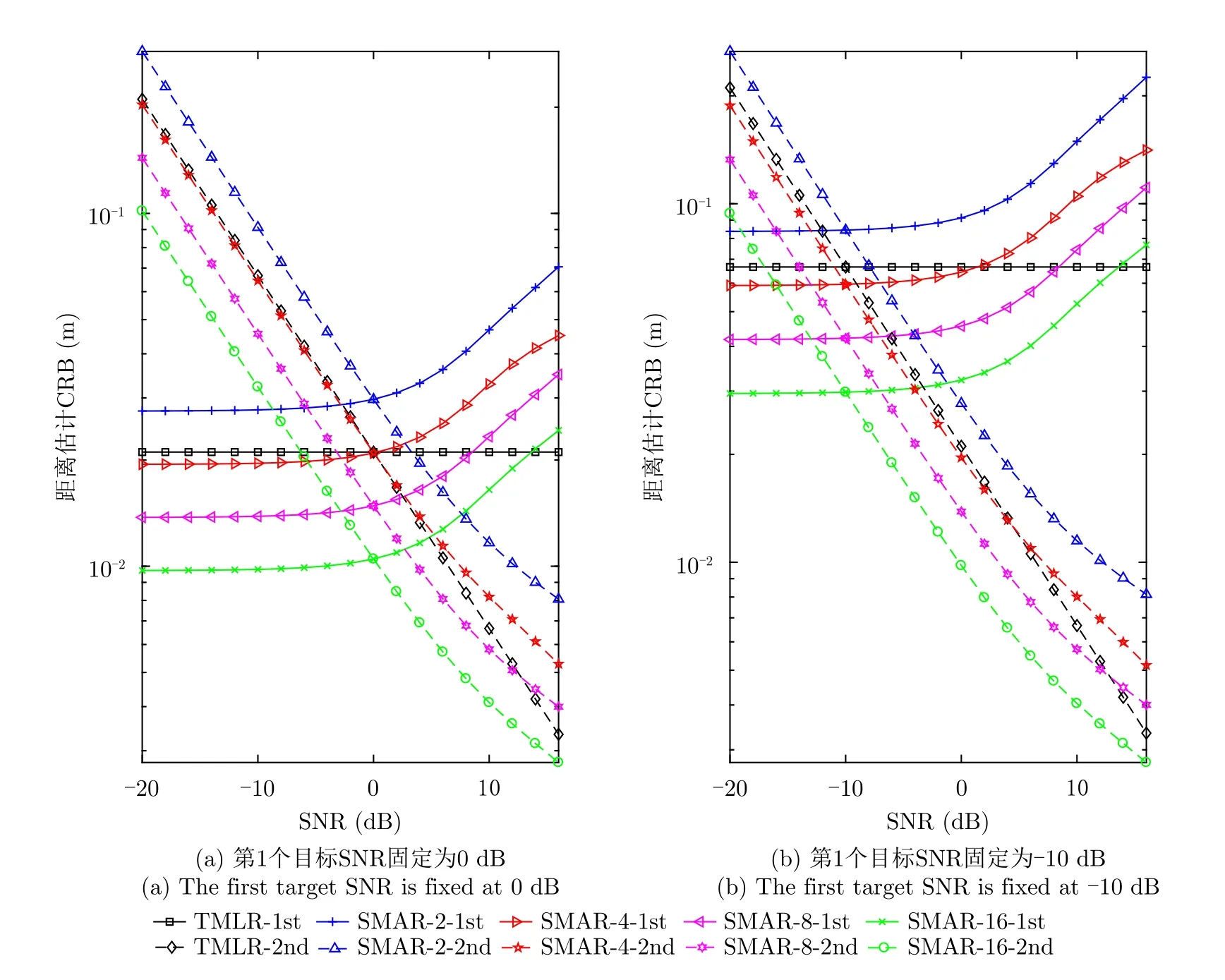
图9 固定第1个目标SNR下的距离估计性能Fig.9 Distance estimation performance under fixed first target SNR

图10 固定第1个目标SNR下的速度估计性能Fig.10 Velocity estimation performance under fixed first target SNR

图11 固定第1个目标SNR下的DOA估计性能Fig.11 DOA estimation performance under fixed first target SNR
单比特采样量化下,当SNR大于等于0 dB时,强目标的存在会降低弱目标的探测精度,当SNR小于0 dB时,强目标并不会影响弱目标的探测精度。这里的强弱是相对的,SNR较大的目标称之为强目标,较小的称之为弱目标。当第1个目标的SNR固定为-10 dB或0 dB时,两个目标测距、测速与测角的CRB曲线均在-10 dB或0 dB处相交,如图9-图11中相同颜色的曲线在-10 dB或0 dB处相交。固定SNR目标的CRB曲线,在第2个目标SNR小于0 dB时,与TMLR一样,保持不变。但当第2个目标的SNR大于等于0 dB时,SNR固定不变的第1个目标的测距、测速与测角精度将随着第2个目标SNR的增加而变差。增加阵元数量,两个目标的探测精度都会显著提升,但也不会改变第2个目标SNR大于0 dB时,第1个目标探测精度会降低的现象。因此,为了保证多个目标的探测性能不会相互干扰,应保证被测目标的SNR均小于0 dB。这是因为当存在SNR大于0 dB的目标时,弱目标信号的波形变化被调制于强目标的信号上,基于过零比较的单比特量化,难以采集到弱目标信号的符号变化,故而弱目标的探测性能受到削弱。
4 数值验证
为了进一步验证SMA获取目标原理的正确性,以及上述理论推导与分析的可靠性,还需要用具体的目标参数估计算法对该系统进行数值验证。
然而,作为一种雷达信号收发的新方式,基于传统滤波理论的目标参数估计方法并不适用于该系统。由于单比特量化方式的引入,经典滤波处理无法消除单比特雷达信号频谱中谐波、交调等分量对真实目标参数估计的干扰。因此,还需寻求一种新的适用于该系统的目标参数估计算法。受文献[24]中单比特MUSIC算法可以有效估计一般阵列信号DOA的启发,本文将其推广到SMA雷达目标多维参数估计上,并用于新系统的数值验证。
4.1 验证算法
步骤1 将第m个阵元接收的单比特信号ym(l,p) 排列成矩阵Ym ∈RP×L,其中Ym的行表示单个脉冲周期内在快时间域的采样数据,列表示多个脉冲周期内在慢时间域采样的数据。
根据反正弦定律[42],式(26)中Y的协方差矩阵RY与X=AS+W的协方差矩阵RX有如下关系:
其中,R Y=YHY/(M(P-Mr+1)(L-Mr+1)),p′为所有目标信号与噪声功率之和。由于arcsin(x)与x在x=0附近十分接近,这使得在低SNR的条件下[24],RY与 2RX/(πp′)中非对角元素近似相等。此外,RY的对角元素均为1,2RX/(πp′)的对角元素均为 2/π。因此,在低SNR的条件下有
其中,E为与R Y同阶数的单位阵。式(30)表明,RY与RX具有相同的特征向量。这进一步说明,式(26)中X对应的噪声子空间可以通过对RY进行特征值分解得到,即RY=UΛUH,其中,Λ和U分别为特征值对角矩阵其及对应的特征向量组成的矩阵。通过取出最小的个特征值对应的特征向量,可以得到噪声子空间接下来,构造二维的MUSIC伪谱函数
可以看出,本文是利用2D-MUSIC来估计两个二维数字频率对,然后在速度维对目标参数进行配对。因此,该验证算法可被称为基于单比特2DMUSIC的速度维配对算法。由以上的讨论可知,该算法最多可以同时估计个目标,目标各维度的参数分辨率受Mr控制。滑窗Mr≤M,同一个bi或gi或hi上的目标个数应均小于或等于Mr。算法的计算复杂度由维矩阵的特征值分解和二维的谱峰搜索决定。
4.2 验证结果
在本节中,我们设置验证算法的参数Mr=8,接收阵元个数为16,目标个数及其参数对与3.3节的保持一致,并设置两个目标的SNR相等。接下来,我们首先绘制当SNR为-10 dB时的慢时间-快时间维和空间-慢时间维的二维MUSIC伪谱图,伪谱的幅度以dB的形式呈现,最亮处表示0 dB,如图12所示。然后,利用4.1节的验证算法估计目标参数,并计算其均方根误差(Root Mean Square Error,RMSE),绘制成如图13所示的曲线。距离估计的RMSE为

图12 归一化2D-MUSIC伪谱俯视图Fig.12 Normalized 2D-MUSIC pseudospectral top view
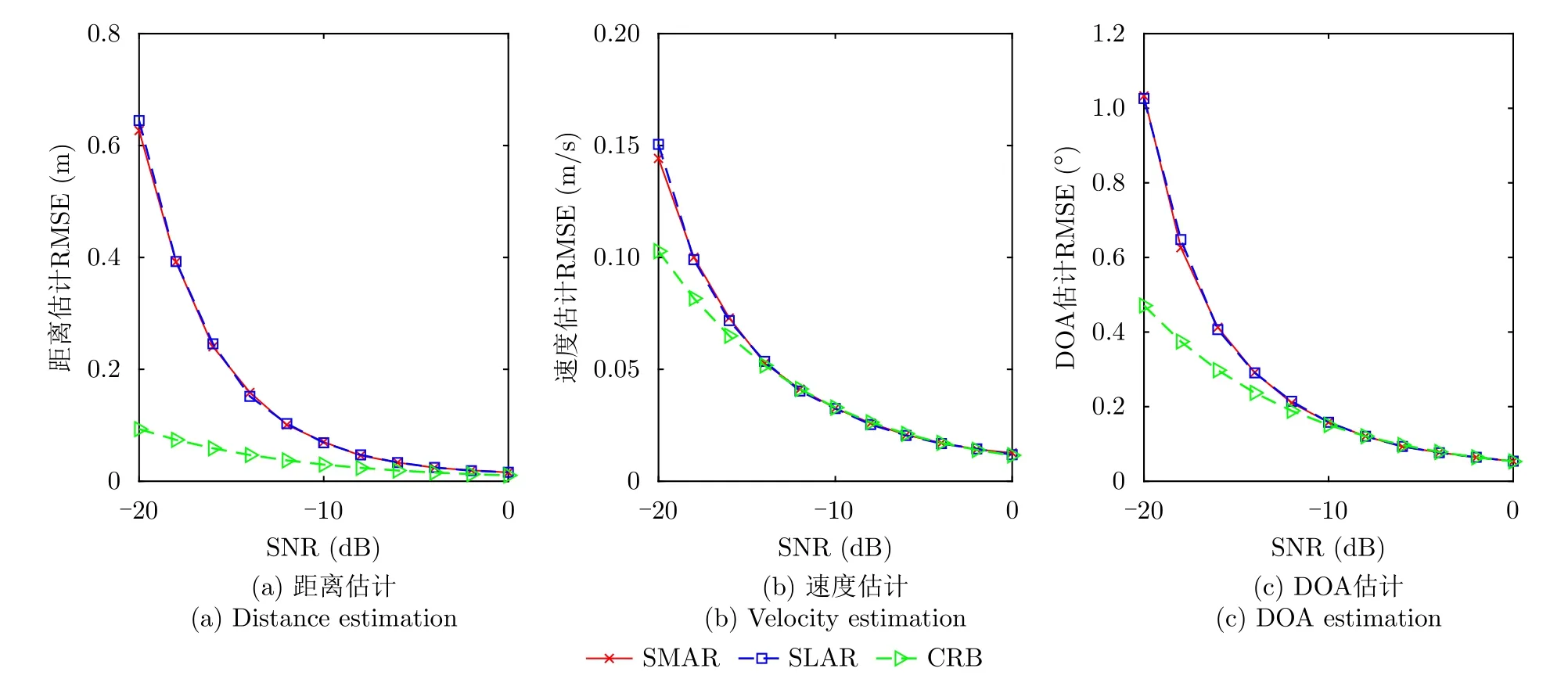
图13 提出算法的估计性能Fig.13 The estimation performance of the proposed algorithm
从图12可以清晰看出两个目标,表明本文提出的单比特二维MUSIC可以用于估计二维频率对从图中可以搜索出h-b维的两个目标分别为(1.5629,2.3303)和(2.5064,1.3994),g-h维的两个目标分别为(0.6573,1.5755)和(-0.7453,2.5064)。根据式(4)和提出的验证算法的配对原则,可以得到估计的两个目标参数对分别为(22.1975 m,7.9780 m/s,-19.6919°)和(37.0404 m,4.9950 m/s,8.4254°),该结果与真实的目标参数对十分接近,这表明了提出的SMAR获取目标原理上的正确性。
图13中SMAR与SLAR估计的RMSE曲线几乎完全重合,与3.3.1节中SMAR与SLAR估计的CRB曲线几乎完全重合的结果一致。这进一步从数值上验证了复用技术的引入,对探测精度的影响较小。此外,随着SNR升高,其目标参数估计的RMSE逐渐逼近CRB曲线,特别是速度维和角度维的估计在SNR大于-10 dB时,和CRB曲线几乎完全重合。这也从数值仿真上验证了第3节中理论推导及其基于CRB分析的可靠性。
5 结语
本文面向低成本轻量级雷达的应用需求,提出了一种SMA雷达信号收发框架。通过对该框架工作原理、应用方式及其资源配置特点的阐述,分析了其低成本、轻量化和高性能目标探测的优势。利用CRB工具,验证了SMA在目标(特别是微弱目标或SNR小于0 dB的目标)参数估计方面的优势,并指出了其稳定工作的SNR应小于0 dB。最后,通过提出一种适用于该框架的目标参数估计算法,并利用数值仿真,验证了该框架目标获取原理的正确性,以及性能分析的可靠性。
尽管框架稳定工作的条件,会降低雷达系统的普适性和通用性,但其低成本、轻量化的特点,以及在相同代价下可获得相比传统雷达更好的探测性能,使得该框架特别适合于小载荷无人机雷达对微小目标探测之类的特殊场景。具体应用例如巡飞弹弹载雷达对炮弹、火箭弹等微小目标的探测。此外,在实际应用中,通过控制雷达作用在不同距离处的发射功率,使其工作在目标SNR小于0 dB的范围内,这对于降低系统能耗具有积极的意义。该特性也进一步表明了SMA在低成本轻量级雷达中的应用潜力。
由于篇幅限制,本文未对目标参数快速估计,以及如何协同控制SMA雷达发射功率等问题进行更深入的阐述,未来的研究工作将聚焦在这些科学问题上。
利益冲突所有作者均声明不存在利益冲突
Conflict of InterestsThe authors declare that there is no conflict of interests

