基于IHPO-KELM 的冷轧带钢板形模式识别①

周亚罗， 张少川， 刘文广， 张瑞成

（1.华北理工大学 电气工程学院，河北 唐山 063210； 2.首钢京唐钢铁联合有限责任公司，河北 唐山 063200）

随着我国经济发展和人民生活水平的提高，板带材的需求量逐渐增加，质量不断提高。 板形模式识别作为板带材产品质量控制的关键技术，成为学术界和行业关注的焦点，同时板形模式识别在板形控制策略的制定中至关重要。

板形模式识别的常见方法有最小二乘法板形模式识别、模糊分类板形模式识别、神经网络板形模式识别等。 在这些方法中，最小二乘法板形模式识别操作简单，但它无法清晰地识别板形较为复杂的浪形。 模糊分类法板形模式识别具有抗干扰能力强、快速稳定的性能，但面对高精度轧机，识别精度不高，达不到高精度轧机的控制要求。 神经网络板形模式识别法具有鲁棒性强、识别速度快等优点［1］，但存在易陷入局部最优解、网络模型建模复杂和网络训练精度较低等缺点。将智能算法与神经网络结合［2-11］已成为当前板形模式识别的主要技术。 虽然这些方法在板形模式识别中均提高了板形识别的精度，但提升效果仍有限，还需进一步研究。

为了解决收敛速度慢、易陷入早熟等缺点，本文提出一种基于改进猎食者算法优化核极限学习机神经网络板形模式识别方法。 在核极限学习机神经网络建模过程中，采用改进的猎食者算法对核极限学习机的正则化系数和核参数同时进行优化，改善板形模式识别的效果。

1 建立板形模式识别

板形是带钢内部残余应力沿板宽方向分布的直观反映，板形模式识别是板形闭环控制的基础，精确的板形模式识别结果是板形控制研究的前提。

1.1 板形基本模式

在冷轧板带生产中常见的板形缺陷基本模式有左边浪、右边浪、中间浪、双边浪、左三分浪、右三分浪、四分浪以及边中浪等8 种。 在板形缺陷基本模式分析中，选择勒让德正交多项式作为板形基本模式，板形缺陷基本模式的归一化方程为：

式中x为归一化板宽，x∈［－1，1］；Yi（i＝1，2，…，8）为各种板形基本模式归一化的板形值。

8 种标准归一化的板形基本模式如图1 所示。

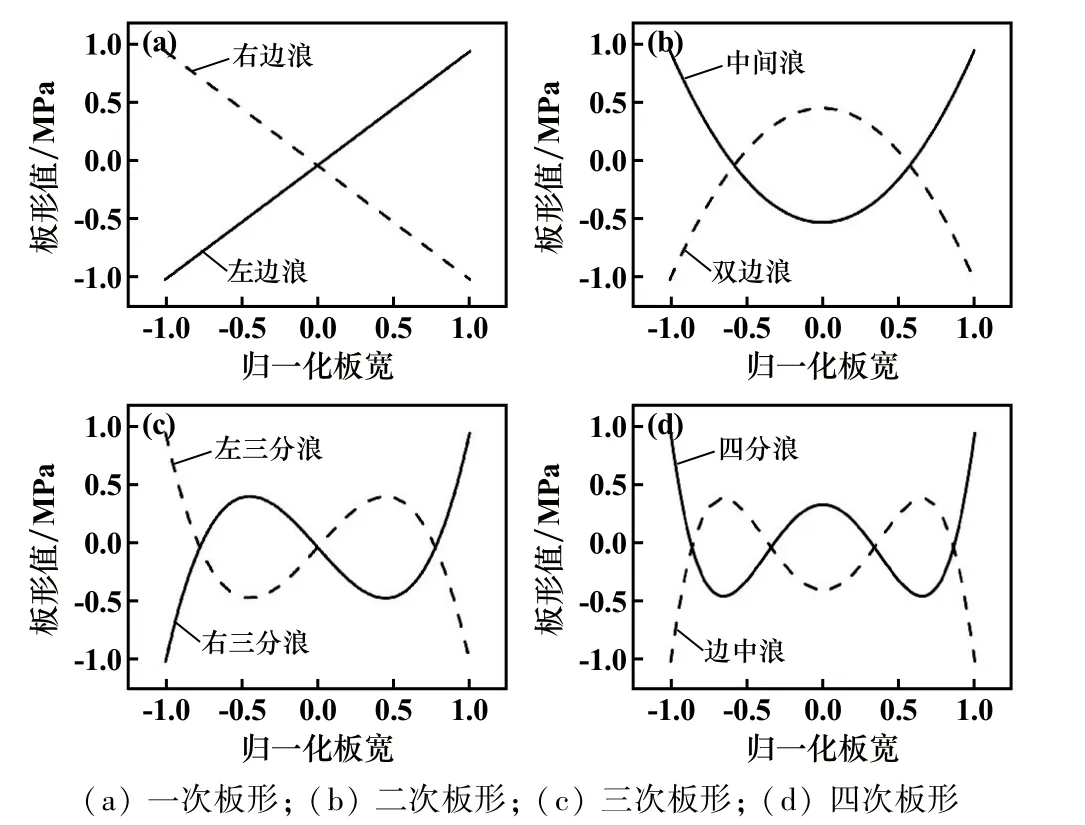
图1 标准归一化的板形基本模式

在实际板形识别中，同一种板形中互反模式不可能同时出现，所以轧后板材的板形可由下列基本板形模式的线性组合表示：

式中a1，a2，a3，a4均为板形特征参数，分别代表一次，二次，三次，四次板形偏差；Yk（k＝1，3，5，7）为板形基本模式归一化的板形值。

1.2 核极限学习机网络

极限学习机（ELM）是一种新型单隐层前馈神经网络，具有输入层、隐含层和输出层三层网络结构。ELM 在学习速度和泛化能力方面具有较大的优势，但容易出现训练结果不稳定以及泛化能力不理想的问题。 核极限学习机（KELM）将核函数思想引入ELM，采用核映射取代ELM 的随机映射，增强了系统的鲁棒性。 将核极限学习机网络应用于板形模式识别中，具有参数少、学习速率快、结果稳定和识别速度快等优点。

KELM 的标准输出F（x）为：

式中δ为核参数。

1.3 基于KELM 网络板形模式识别模型

在板形模式识别中，识别模型的输入采用待识别样本与板形基本模式的欧氏距离。 将实测板形应力值离散为m个点位，待识别样本归一化为X＝［σ（1），σ（2），…，σ（m）］，第k个基本模式为Xk＝［σk（1），σk（2），…，σk（m）］（k＝1，2，3，…，8），计算待识别样本X与第k个基本模式Xk之间的欧氏距离：

式中Dk和Dk＋1为两个互反模式的欧式距离差。

因此将DD1，DD2，DD3，DD4作为IHPO-KELM 网络的输入，网络的输出为板形特征参数的隶属度μ1，μ2，μ3，μ4，如果要得到实际的板形特征参数a1，a2，a3，a4，则需要对μ1，μ2，μ3，μ4反归一化处理：

式中i＝1，2，…，m；j＝1，2，3，4；Δσi为待识别板形与目标板形的板形偏差。

综上所述，KELM 网络结构为4 个输入层结点和4 个输出层结点。 其中，待识别样本与板形基本模式的欧氏距离DD1，DD2，DD3，DD4为KELM 网络的输入，板形特征参数a1，a2，a3，a4为KELM 网络的输出。网络的拓扑结构如图2 所示。

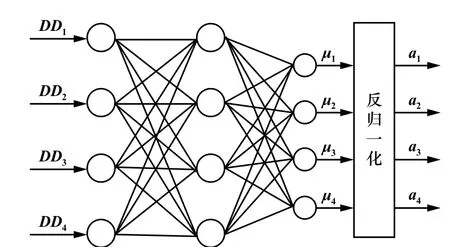
图2 KELM 网络拓扑结构

2 改进猎食者算法优化核极限学习机网络的板形识别模型

在板形模式识别中，核极限学习机网络的形式取决于核参数以及正则化系数。 在基于核极限学习机网络的板形模式识别［10］方法中只针对核函数的核参数进行寻优，而正则化系数需要依靠人为的经验选取，这对板形模式识别的精度有一定影响。 因此，采用改进的猎食者算法对核极限学习机网络中的核参数δ和正则化系数λ同时进行优化，提高板形识别的速度以及精度。

2.1 猎食者算法

猎食者算法（HPO）［12］是2022 年提出的一种基于种群的新优化算法，具有收敛速度快、寻优能力强等优点。 首先HPO 算法在解空间中随机初始化种群位置，种群初始化公式为：

式中xi为第i个猎人或猎物的位置；ub和lb分别为搜索空间的最大值和最小值；d为搜索空间的维度。

猎食者和猎物的位置更新公式为：

式中Ppos（j）为猎物的位置；μ为所有位置的平均值；x（t），x（t＋1）分别为猎物当前位置和下一次迭代位置；Tpos为全局最优位置；R4为［－1，1］的随机数；R5为［0，1］的随机数；β为一个调节参数，若R5＜β，则搜索代理被视为猎食者，若R5≥β，搜索代理将被视为猎物；C为探索和开发之间的平衡参数，其值在迭代过程中从1 减小到0.02；Z为自适应参数，其计算公式为：

2.2 基于改进猎食者算法

猎食者算法在寻优过程中易陷入局部最优，种群多样性少，进而影响算法的全局最优值，导致板形模式识别的精度不足。 需对猎食者算法进行改进，提高算法的寻优能力。

2.2.1 Sine 混沌映射初始化种群

Sine 映射［13］由正弦三角函数变换得到，由于Sine映射分布不均匀、概率密度差异较大，采用一种改进型Sine 混沌映射［14］，其产生的序列初始化种群，在增强种群多样性的同时，提升算法前期的收敛速度。 具体如下：

式中γ为常数；gbest为个体最佳位置。

2.3 基于IHPO-KELM 的板形模式识别

利用IHPO 算法优化KELM 网络的核函数δ和正则化系数λ，能够有效避免人工选择参数的随意性和盲目性。 将KELM 网络中待优化的两个参数核函数δ和正则化系数λ映射到改进的猎食者种群中，待优化的两个参数转化成猎食者个体的当前位置，通过不断更新迭代，寻得猎食者种群中最优位置，最优位置的数值代表待优化参数的取值，即最优解为IHPO-KELM板形模式识别模型的参数。

算法步骤如下：

1） IHPO 种群数量选取为N个，将其位置作为待优化参数，根据改进型Sine 混沌映射初始化种群。

2） 将粒子的位置作为核极限学习机的正则化参数和核参数，通过式（10）计算出板形模式识别的结果，求得与真实值的均方根误差（RMSE）。

3） 通过线性组合与莱维飞行机制改进的猎食者位置更新公式，根据每组RMSE 更新猎食者和猎物的位置。

4） 重复步骤2）和3），同时记录N组粒子中的最优位置，直到满足RMSE 达到设定的范围或达到最大迭代次数的要求。

5） 将最优位置作为最优参数应用到式（11）中，求出核极限学习机中的核函数。

6） 计算IHPO-KELM 板形模式识别模型的输出，即板形特征参数。

适应度函数选取为板形特征参数的真实值与板形模式识别结果的均方根误差（RMSE）：

式中yreal为标准输出；ypre为识别结果；n为样本集个数。

基于IHPO-KELM 板形模式识别的流程如图3所示。

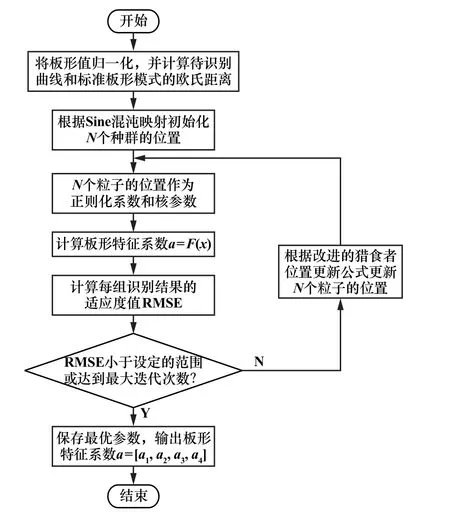
图3 基于IHPO-KELM 板形模式识别流程

3 仿真实验结果对比分析

采用基于IHPO-KELM 板形模式识别模型，本次实验构造了10 000 组板形标准样本数据集，其中的70%用作网络的训练数据，剩下的30%作为测试数据，检测点选取为37 个，适应度函数选取为均方根误差（RMSE）。

IHPO-KELM 算法主要参数选择：种群规模N为50，最大迭代次数Maxit为50 代，种群的上下界ub和lb分别为［1 000，1 000］、［0.001，0.001］，步长因子α为0.01，莱维飞行机制中参数γ为1.5，控制参数u为1 500，调节参数β取值0.1，维度d为2。

通过50 次迭代优化运行，最后寻得最优的正则化系数为531.16，最优核参数为0.088。 参数未优化的KELM 正则化系数和核参数分别取4 和20。 表1 为随机选取3 组未经过训练的测试集输出结果以及与标准输出的均方误差（MSE）。 从表1 可以看出，基于IHPO-KELM板形模式识别模型在识别板形特征参数和均方误差MSE 均优于麻雀算法优化的核极限学习机识别模型（SSA-KELM）和参数未优化的KELM 模型。 这表明改进的猎食者算法识别的精度更高。 MSE 的计算公式为：

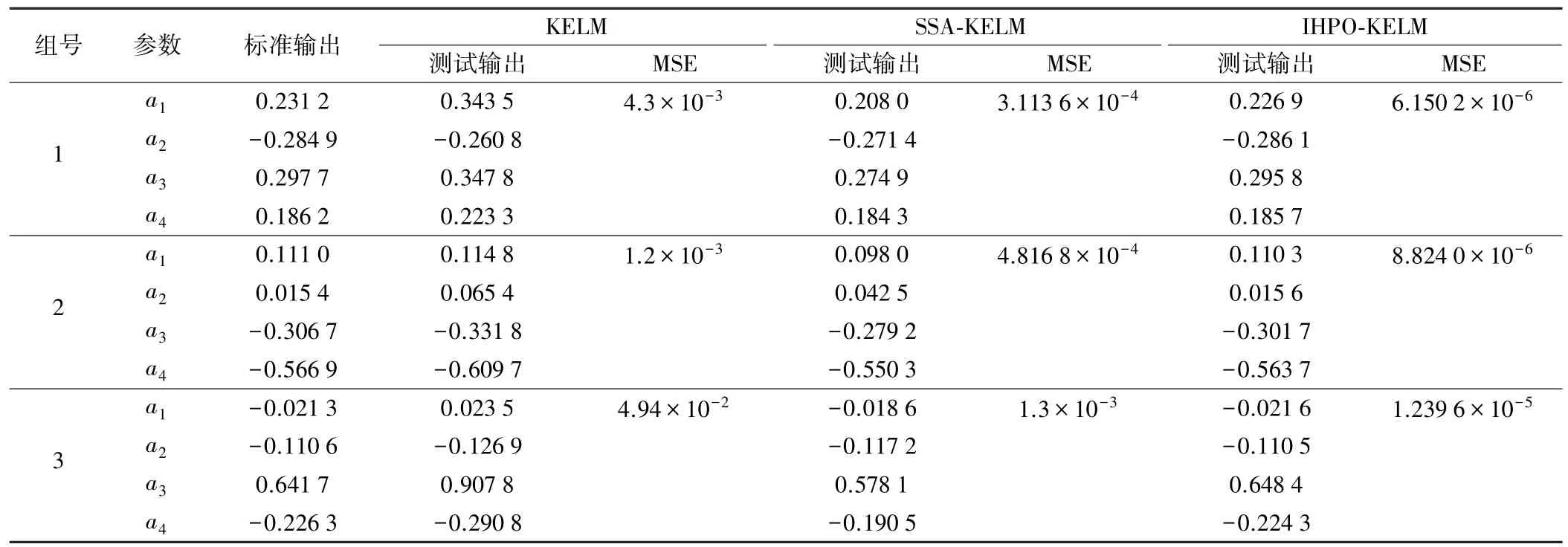
表1 3 种方法板形模式识别结果及均方误差

式中yreal和ypre分别为标准输出和测试输出；n为样本集个数。

图4 为SSA-KELM 的收敛曲线，达到收敛稳定需要17 代，适应度曲线趋近于0.009 5。 图5 为IHPO-KELM的收敛曲线，达到收敛稳定只需要6 代，适应度曲线趋近于0.007。 通过比较，IHPO-KELM 网络训练性能优于SSA-KELM，训练时间更短，收敛速度更快。

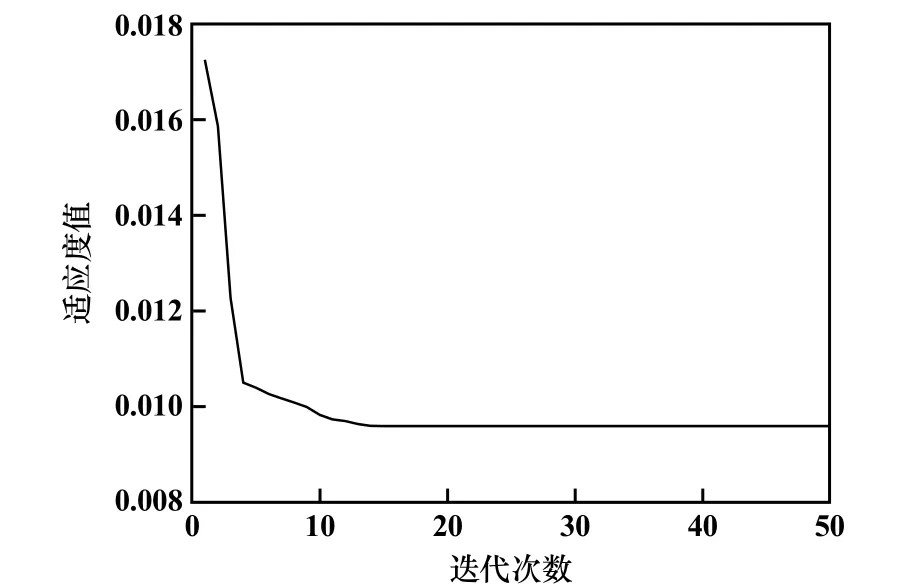
图4 SSA-KELM 收敛曲线

图5 IHPO-KELM 收敛曲线

以表1 第1 组样本为例，将IHPO-KELM、SSA-KELM、KELM 以及标准输出绘制成曲线，如图6 所示，可以看出，IHPO-KELM 的拟合效果最好。

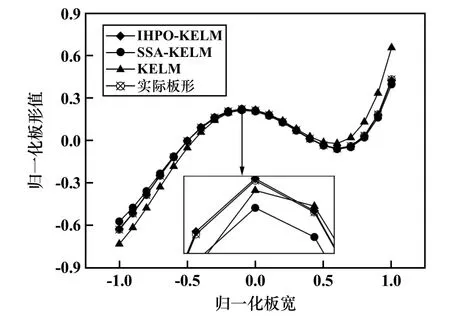
图6 板形识别对比曲线

为了验证IHPO-KELM 在实测数据中的识别能力，在MATLAB 2021a 环境下，将上述训练后的IHPOKELM 板形识别模型应用到某钢厂900HC 可逆冷轧机第五道次的板形识别中。

第1 组样本的归一化板形数据为［0.197 1，－0.077 4，－0.191 8，－0.193 1，－0.122 6，－0.015 2，0.099 9，0.200 0，0.268 0，0.293 3，0.271 2，0.202 9，0.096 0，－0.036 2，－0.174 0，－0.291 8，－0.357 8，－0.334 4，－0.177 7，0.162 2，0.741 4］，将实测数据通过不同的板形识别模型进行仿真分析，识别结果如表2 和图7所示。

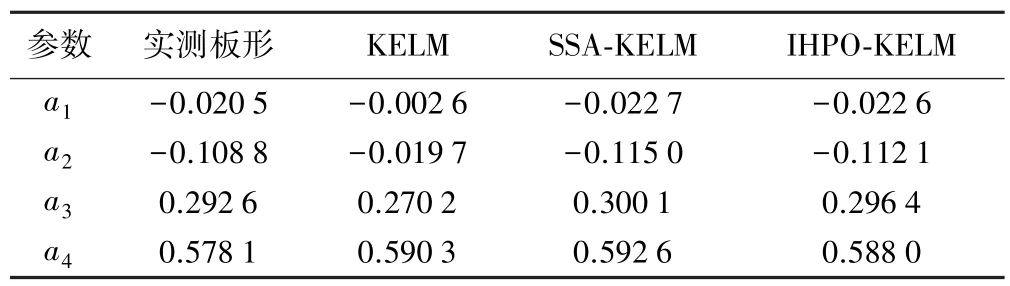
表2 3 种方法的板形缺陷识别结果

图7 识别的板形整体曲线

根据式（25），计算得到IHPO-KELM 模型、SSA-KELM模型、KELM 模型的均方误差MSE 分别为3.19×10－5、7.75×10－5和0.004。 IHPO-KELM 识别精度比SSA-KELM识别精度提高了58.8%。

通过图7 可以看出，3 种板形模型中，参数未优化的KELM 识别效果最差。 由于SSA-KELM 与IHPO-KELM曲线相近，通过局部放大可以清楚地看到IHPO-KELM 模型拟合效果最好，最接近真实信号，表明IHPO-KELM 模型在实际应用中具有识别精度高、识别速度快及良好的泛化能力等优点。

由图7 识别的整体曲线可知，板形缺陷是由图8所示的右边浪、双边浪、右三分浪和四分浪4 种缺陷组合而成的，在后续的板形控制中可以根据识别的板形不同分量采取相应的调控手段。

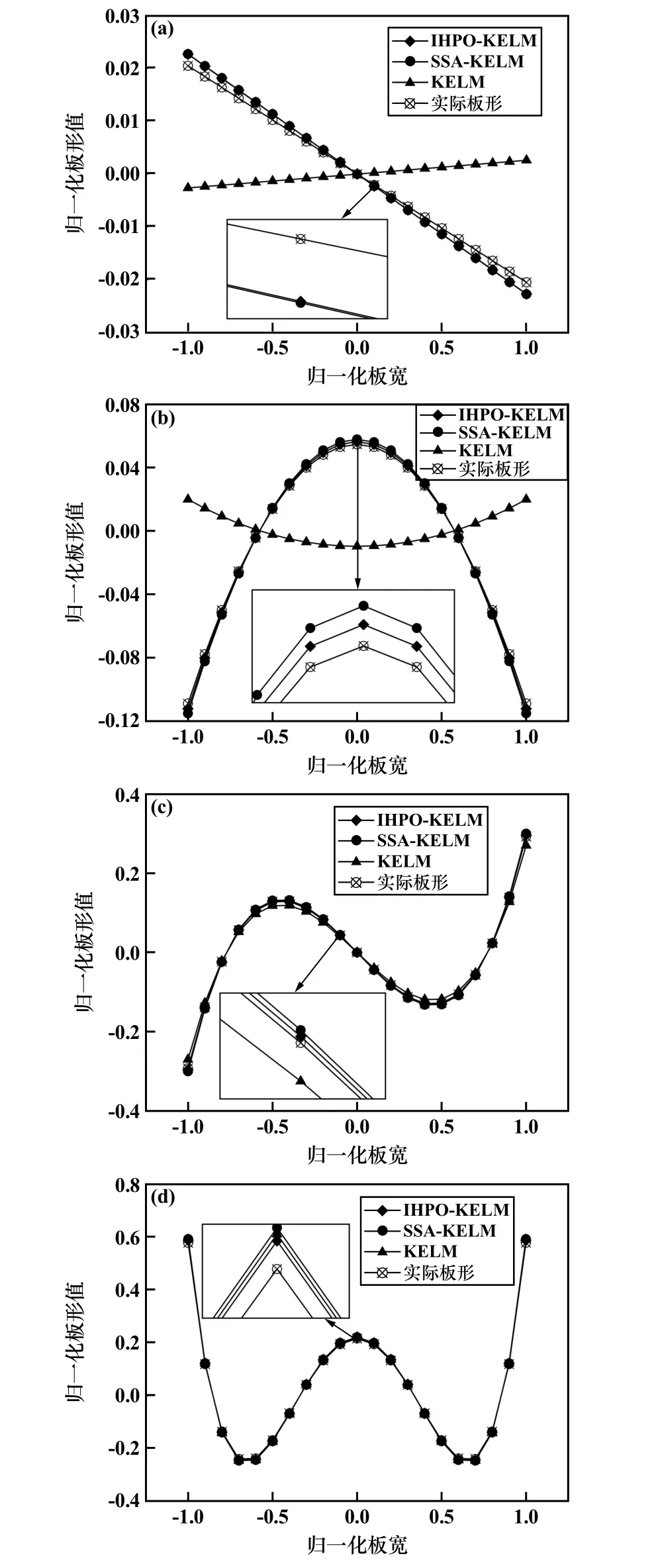
图8 不同板形识别曲线

4 结 语

1） 引进Sine 混沌映射和改进位置更新公式的猎食者算法提高了种群的多样性，增强了算法的全局寻优和局部开发能力，收敛速度更快。

2） 采用改进猎食者算法同时优化核极限学习机的正则化系数λ和核参数δ，构建了基于改进猎食者算法优化核极限学习机的板形识别模型，为板形缺陷的高效智能识别提供了新思路。

3） 仿真实验验证了IHPO-KELM 冷轧带钢板形识别模型具有识别精度高和泛化能力强的优点，对于今后的板形控制有积极的指导作用。