应用统计法解决晶体结构相关问题的探索——基于模型认知素养水平的视角

陈达明 张贤金

(1.福建省惠安第一中学;2.福建教育学院化学教育研究所)

模型认知是指借助模型认识事物及其变化,或通过建构认知模型形成解决问题的思考方法。模型认知是化学学科核心素养之一,也是化学学习的重要手段。模型认知不但使化学学习具有体验性与过程性,而且它生成的结论、规律与方法可直接应用于化学问题的解决。

晶胞分摊法是长期以来解决晶体结构相关问题的基本模型,该模型的关键是推断一个晶胞中某种微粒的实际个数,即等于晶胞中某微粒的数目除以共用该微粒的晶胞数。课堂教学中教师会与学生一起对这一基本模型进行建构与认知、验证与应用,在解决实际问题时却发现其局限性明显,具体表现在:晶胞分摊法用于解决微粒与微粒之间的关系及数目比进而推断化学式是很方便的,但是在推断微粒与化学键或微粒与微粒形成的环的关系时就不好入手。教学过程中生成的问题往往是可利用的资源,基于对旧模型应用广泛性的怀疑进而产生在模型拓展基础上建构新模型的源动力,新的模型又是如何应运而生的呢?

长期的教学实践告诉我们,新的方法、规律结论、模型一般都来源于教材的二次开发,基于教材又高于教材的知识更具有实用性,其生成的过程无疑对于发展能力、形成核心素养是非常有效的。有了这样的认识,笔者就组织学生阅读教材相关内容,设置情境进行思考,总结归纳形成结论。人教版高中化学选修3《物质结构与性质》(2009版)第78页至第79页关于配位数的探究除了要懂得影响微粒配位数的原因和如何确定配位数外,似乎还隐含着建构统计法这一模型的基础。师生互动中完全可以得出这样的推理:1个Na+周围距离最短且相等的Cl-有6个,即Na+的配位数为6;1个Cl-周围距离最短且相等的Na+有6个,即Cl-的配位数也为6;所以两种微粒的个数比为6∶6=1∶1,则氯化钠晶体的化学式为NaCl。基于教材的探究活动内容的二次开发应用形成了新的解决晶体结构的模型,该模型是通过统计晶体中距X微粒最近且距离相等的Y微粒数(即X的配位数a)和距Y微粒最近且距离相等的X微粒数(即Y的配位数b)从而求得化学式为XbYa,可以称之为统计法,实际应用中,统计法不但可以确定化学式,还广泛地用于推断晶体的各组成成分之间的关系。

《普通高中化学课程标准》(2017年版2020年修订)关于化学学科核心素养教学的模型认知又分为四个素养水平,有了统计法并结合晶胞分摊法,我们在解决实际问题的教学时就能充分体现这四个素养水平,下面对试题教学略作探讨。

一、推断构成微粒之间的关系

素养水平1:能识别化学中常见的物质模型和化学反应的理论模型,能将化学事实与理论模型之间进行关联与合理匹配。

首先,必须掌握教材中各类晶体代表物的结构模型,如NaCl、CsCl、干冰、晶体碘、金刚石、晶体硅、SiO2、石墨等,实际解题时才能将未知模型与已知模型进行关联与匹配;其次,应用统计法这一解题的基本模型去直接进行推理、得出结论并与晶胞分摊法进行融合使用。

【例1】高温下,超氧化钾晶体呈立方体结构,晶体中氧的化合价部分为0价,部分为-2价。如图甲为超氧化钾晶体的一个晶胞(晶体中最小的重复单元),则下列说法中正确的是________。

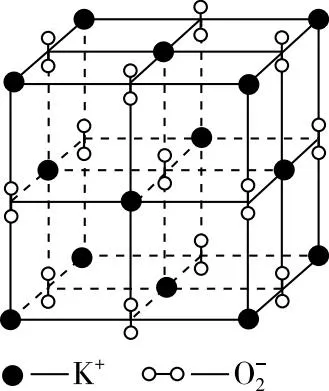
甲

乙

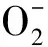
C.晶体中与每个K+距离最近的K+有8个

D.晶体中,0价氧与-2价氧的数目比为3∶1

【答案】AD

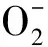
本题的教学不仅可以引导学生复习典型离子晶体结构模型,还可让学生就具体案例建构统计法模型,充分感受统计法模型原型认知的过程,并直接就教材模型与试题模型进行关联与匹配,进而达成素养水平1。

素养水平2:能理解、描述和表示化学中常见的认知模型,指出模型表示的具体含义,并运用模型解释或推测物质的组成、结构、性质与变化。

这仍然是就模型本身的内容而言的,根据模型的内涵回答相关问题并作出解释,但明显在知识综合运用及思维能力方面的要求比素养水平1高。

【例2】如图表示锌与某非金属元素X形成的化合物晶胞,其中Zn和X通过共价键结合,该化合物的化学式为________;该化合物的晶体熔点比干冰高得多,原因是________________;距一个X原子最近且距离相等的Zn原子有________个,Zn形成的空间构型是________。

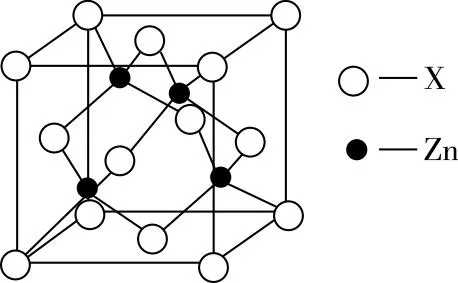
【答案】ZnX ZnX是共价晶体而干冰是分子晶体 4 正四面体形

本题教学先引导学生联系金刚石晶体结构模型进行匹配推断该晶体为共价晶体,再由共价晶体模型与分子晶体模型知识解释物理性质;由统计法模型的含义迁移到X的配位数的推断,进一步推理其周围4个Zn形成的空间构型,从而达成素养水平2。

二、推断构成微粒与微粒间化学键之间的关系

素养水平3:能对模型和原型的关系进行评价以改进模型,能说明模型使用的条件和适用范围。

基于教材的统计法模型原型解决的是构成晶体的微粒之间的关系并推断化学式,如果题型要解决的是构成微粒与化学键的关系,只需对原模型稍加改进,把微粒与微粒的类比关系改为微粒与化学键或化学键与正六边形的类比即可,具体看下面的例题解析。

【例3】(1)金刚石晶体结构如图甲所示,则12 g金刚石晶体中含有的化学键数目为________。

(2)石墨晶体结构如图乙所示,每一层由数个正六边形构成。平均每个正六边形所占有的碳原子数目为________,平均每个正六边形所占有的共价键数目为________。

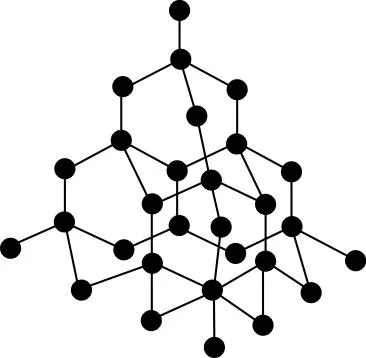
甲

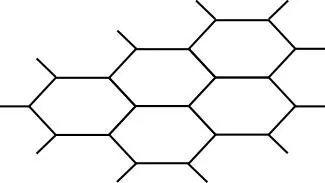
乙

【答案】(1)2NA(2)2 3

【解析】(1)观察甲图可知:1个C原子周围有4个碳碳键,1个碳碳键周围有2个C原子,所以碳碳键与C原子的数目比为4∶2=2∶1;12 g金刚石含1 mol C原子,则碳碳键数目为2NA(NA为阿伏加德罗常数)。(2)观察乙图可知:1个正六边形有6个C原子,1个C原子周围有3个正六边形,C原子与正六边形数目比为6∶3=2∶1,故平均每个正六边形所占有的碳原子数目为2;1个碳碳键周围有2个正六边形,1个正六边形周围有6个碳碳键,正六边形与碳碳键的数目比为2∶6=1∶3,故平均每个正六边形所占有的共价键数目为3。

教学时先提出问题,让学生清楚本题要探究的是碳原子与碳碳键的关系及碳原子与碳原子形成的六元环的关系,而统计法模型原型解决的是微粒与微粒间的关系,两者貌似不同,但类比、讨论后发现它们实际是相似的。因而在原型基础上得出改进模型,那便是统计法模型研究的对象可以拓展到两个相关因素的关系而不单单是微粒间的关系,这样素养水平3就形成了。

三、推断构成微粒与微粒所形成的环之间的关系

素养水平4:能对复杂的化学问题情境中的关键要素进行分析以建构相应的模型,能选择不同模型综合解释或解决复杂的化学问题;能指出所建模型的局限性,探寻模型优化需要的证据。

在教学中建构统计法模型本身就体现了这一素养水平,它高于前面三个素养水平层级,在解决实际问题时,也需要在基本模型的基础上建构改进模型,并就模型原型及其几个改进模型在不同问题情境中进行切换;就如我们这里所举的四个例题一样,解决微粒间关系、微粒的配位数、推断化学式使用统计法模型原型便可,但要解决微粒与化学键或微粒与微粒形成的环等之间的关系就得使用原型基础上改进的模型。

【例4】单质硼有无定形和晶体两种,已知晶体硼结构单元是由硼原子组成的正二十面体,其中有20个等边三角形的面和一定数目的顶点,每个顶点上各有1个B原子。通过视察图形及推算,此晶体结构单元由________个硼原子构成,其中B—B键的键角为________。如果把每个顶角整齐切去,形成由一些五元环与六元环构成的足球烯,则五元环有________个,六元环有________个。

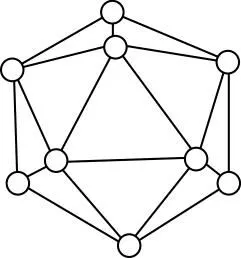
晶体硼

【答案】12 60° 12 20

【解析】如图,切去顶角便由图Ⅰ变为图Ⅱ,直接应用统计法求B原子数目,即1个B原子周围有5个三角形,1个三角形周围有3个B原子,可见三角形与B原子的数目之比为5∶3;设B原子数为a,三角形有20个,故20∶a=5∶3,求得a=12。切去顶角,12个顶角就形成12个五元环,20个三角形就形成20个六元环。

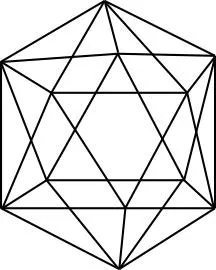
图Ⅰ

图Ⅱ

实际上,素养水平4是在具备前述三个素养水平的基础上综合形成的,教学时既要应用统计法模型原型,根据B原子与三角形两个关键因素建构相应模型后列式计算得出B原子数;又要根据模型含义回答相关问题;还要选择不同模型迁移解决体现五元环与六元环等因素的化学问题。

当然,化学学科核心素养的五个方面以及每个方面的若干素养水平只是相对独立进行划分的,往往不是一一对应、割裂清楚,而是互相交叉、普遍联系、彼此交错在一起的。教学内容以及问题情境的设置只能突出而不可能全部是某一素养或某一素养水平的发展,所以对于模型认知的四个素养水平的教学问题设置只是相对的,不可能完全绝对地体现某一素养水平。上述的四个例题只是突出某个素养水平的教学的分析,而同一个问题的不同方面的设置通常以不同角度来体现不同的素养水平,它们在同一内容、情境或问题中通常会同时具备。

综上所述,如果不注重核心素养的学习,不在体验学习中建构统计法模型,单靠分摊法要解决结构问题是比较困难的。有了统计法这一模型,上述这些困扰我们很久的具有代表性的晶体问题的解决就比较容易了。让学科核心素养在课堂落地,体验基于模型认知的学习,感受解决问题式学习的价值,这是师生完成由知识、能力到核心素养发展的途径之一。