双馈风电机组次同步振荡自主学习控制方法设计

李宗泽，胡桂军

（河北新天科创新能源技术有限公司，张家口 075000）

引言

国内的用电量每年大幅度攀升，为了提高电力功率的开发，增加电力传输的距离，近年来逐渐开始实行风电并网，不仅能大大提高输电能力，还能在一定程度上减少网损率，满足大量的电力需求。经过多方实践和研究证明，风能作为一种清洁能源，在与电力系统融合时，能有效地改变电力的逆向分布特征，同时改善传统发电带来的环境污染。利用双馈风电机组实现风电并网，能提升电能输送能力，但存在的弊端则是很容易产生次同步振荡，影响风电网系统的稳定性，对电网产生一定的危害，因此有效地控制次同步振荡是必要的。相关学者一直深耕该领域，也取得了一些较好的办法。

吴熙等人[1]在研究双馈机并网过程中产生的次同步振荡控制方法时，提出自适应控制方法，建立精度控制模型，通过对参数结构的有效固定，通过改变附加阻尼的实时强度，在动态线性环境相爱，通过输入双馈风电机组的数据特征，完成动态控通过制；马天辉等人[2]在研究中电平换流器实现对风电机组的柔性输电，建立协同控制策略，在柔性直流输电条件下，有效地增加针对次同步振荡的控制能力，搭建风电场的阻尼控制方案，实现对次同步振荡的有效控制。

上述方法缺少一定的自主学习能力，虽然也能取得一定的控制效果，但是对次同步振荡的控制参数的关联性分析，还缺少一定的理论支持。本文提出一种双馈风电机组次同步振荡自主学习控制方法，力图在传统研究的基础上，给出优化解决方案。

1 双馈风电机次同步振荡问题的提出

考虑到双馈机组中风能的分布特征，风电场通常建于较为偏远的区域，这导致输电线路相对较长，在研究双馈风电机的次同步振荡问题过程中，需要将线路电感考虑进去，线路长短直接影响输出端电压，为了抵消线路感抗，增加相应的串联补偿电容，研究中假设额定功率为1.5 MW 的双馈风电机共有n台，并组成机组与电网对接[3]。

为了有效地分析双馈风电机组运行过程中产生的次同步振荡问题，在这一节首先分析次同步频段内的振荡等效电路机理：

通常情况下双馈风电机运行支路对应的等效阻抗为正，对应的变化幅值大于定转子运行支路阻抗，此时运行支路对谐振频率的影响极小，可以暂时忽略。因此在双馈风机的分析中，将运行支路视为开路[4]。建立简化后的双馈风机对应阻抗[5]：

式中

Zdfi—双馈风电机的运行等效阻抗；

ωp—谐振电流的振动角频率；

ωs—定子角频率；

ωr—转子角频率；

Rs、Rr—定子和转子的电阻；

Lls、Llr—定子和转子的运行漏感；

Kip、Kii—短路电阻电流内部调节器的调节比例和调节系数；

Kd—d、q轴之间存在的交叉耦合项；

σp—双馈风电机的次同步转差率[6]。

将双馈风电机的电阻和电感表示为Rd、sLd，这有利于在复频域条件下对风电机串联补偿的研究，这种条件下获取的等效阻抗电路图为图1。

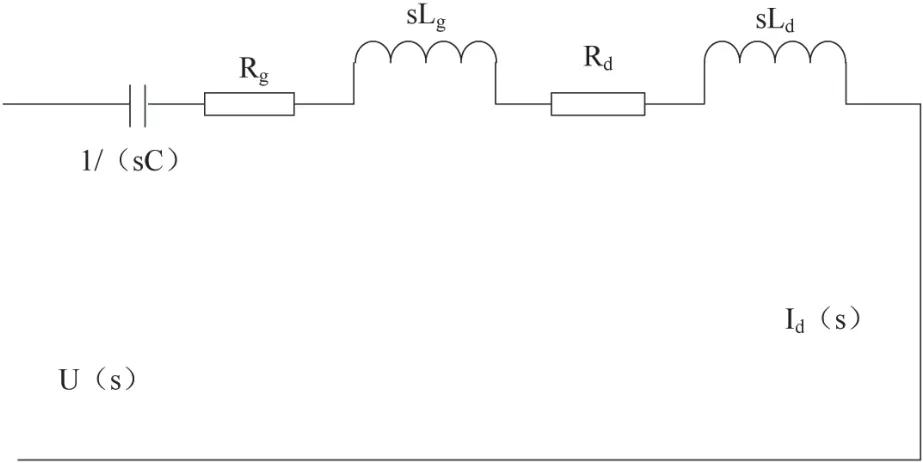
图1 等效阻抗电路图

根据图1 可知，R g、Lg对应的是线路的电阻和电感，C表示双馈风电机的串联补偿电容，Isub(s)表示双馈机的次同步电流，U(s)表示幅频域条件下与同步电流对应的总电压。

式中：

sLg—风电机组电感。

双馈风电机正常运行状态下，发生谐振频率时对应的容抗和感抗之和应为0，考虑到这一点可以得到正常运行状态下谐振点的等效阻抗[7]：

当Rd+Rg＜ 0时，谐振电流受到负电阻影响，逐渐放大后导致发生功率次同步振荡。通过分析简化的双馈风机对应阻抗和等效阻抗电路图，描述了双馈风电机的运行等效阻抗、谐振电流、串联补偿电容等参数。并且指出了在正常运行状态下，谐振点的等效阻抗应为0，但由于谐振电流受到负电阻影响，逐渐放大后会导致发生功率次同步振荡。因此，阻抗调整是解决次同步振荡的主要方法。

2 双馈风电机次同步振荡控制中的转差率约束关系分析

通过上一章节可以看出，当双馈风电机在完成串联补偿时，可能会发生电气的自激振荡情况，双馈风电机整体的次同步振荡将会增加，由于其中包含了感应发电机效应的振荡路径，此时，次同步振荡频率受到多方面因素的影响：其中包括串联补偿效应、变压器状态以及线路的等效容感参数，为了使次同步振荡的控制能更加全面，需要准确掌握次同步振荡中，这些参数存在耦合关系，不能同时作为约束条件，带入到控制方法中。本文以转差率作为约束条件，下面证明其可行性：

双馈风电机的次同步振荡转差率为：

式中：

fs—风电机定子侧三相电压对应的频率；

fm—转子的机械转动频率[8]。

考虑到同步振荡转差率中存在的振荡分量，假设对应的交流频率在7 Hz 左右，那么此时双馈风电机组的转子范围在（40～60）Hz 范围内，次同步转差率的数值均为负，风机转速较低时，相对应的fm值也会较小，此时获得的R rσp绝对值则会变大，间接使双馈风电机组中的电阻成分更容易被抵消，导致风电网中的弱阻抗现象更加严重[9]。

在风电网的回路中，如果存在一定程度的次同步转差率分量，那么双馈风电机组中将会产生扰动电流，此时导致的变流器的输出电压发生波动[10]：

式中：

n—风电网的回路数量；

Δis—谐振频率变化量；

Kp—双馈逆变器的电路回流比例次数。

在双馈风电机组的运行中，产生的激磁电抗相对于定转子漏抗[11]会更多，此时可以得到总等效电阻并表示为：

式中：

Rr—转子电阻；

Rs—定子电阻；

R—风电机组的实施变化电阻。

根据公式（7）中对总等效电阻的求解，在其中增加了一定的负阻尼，表明逆变器额实际作用对象为感应发电机效应产生的次同步振荡，而振荡中的具体成分受到变流器控制后，逐渐形成正反馈，次同步电流在这个过程中逐渐增大，形成双馈风电机正向激励，当感应发电机效应不再产生振荡时，风电网的运行振荡也会更快发散，双馈电机的负阻尼大小跟随风电机的转速而发生实时变化，转速越低时负阻尼的绝对值会越大，此时双馈风电机组系统的阻尼相对薄弱，考虑到次同步成分在转子电压上的作用情况，获得定转子之间的电压关系[12]：

式中：

N—双馈风电机组的定转子匝比；

ur—转子电压；

ur—定子电压。

通过上述分析可知，正常运行状态下的双馈风电机组中转子对应的全频率范围在（40～60）Hz，实际的转差率范围在正负0.2 之间，而当次同步范围在7 Hz 时，实际的转差率范围在-7.5 到-4.6 之间，即使是微小的次同步分量，也会在双馈风电机的转子侧产生较为严重的电压压力，在一定程度上增加风电网的适应难度。次同步频率的高低，对转差率有着一定的、影响，当频率越低时，导致转子电压的次同步成分越大。研究中得出次同步振荡时针对转差特性[13]的研究结果，如表1 所示。

表1 转差特性放大效应研究

通过分析双馈风电机的转差率、转子电压与定子电压之间的关系，了解不同频率范围下次同步振荡的特性和影响。在次同步频率较低的情况下，转差率范围较大，导致双馈风电机转子电压承受较大压力，增加了风电网的适应难度。同时，表1 中给出了针对转差特性的研究结果，进一步揭示了次同步振荡时的转差率特性，因此，以转差率作为控制约束，是可行的。

3 转差率约束下次同步振荡控制方法设计

基于上述的双馈风电机次同步振荡机理与特性分析结果，文中选择利用多目标深度学习进行次同步振荡控制，由于深度学习具备较强的自适应分析能力，能通过简单的结构完成难度较大的训练，由于双馈风电机组的数据较多，因此深度学习模型中，除了基础的输入层、隐含层和输出层之外，将隐含层的数量设置为6 层。深度学习状态可表示为：

式中：

w—深度学习迭代权重；

b—偏置条件；

f(· )—深度学习的激活函数；

a—学习层数；

wi—输入层神经元；

xi—输出层神经元；

j—深度学习状态；

ym—针对双馈风电机组的多目标深度学习目标；

wim—分析提取风电机组次同步振荡所须的迭代权重；

bm—机组偏置[14]。

选择合适的转差率数据作为约束，将振荡中的串联补偿效应、变压器状态以及线路的等效容感参数作为输入，实现多目标深度学习训练。具体的控制过程如下：

通过第一章节内容可知，在转子侧控制阻尼，这在一定程度上可以获得与转速变化相反的电磁转矩[15]，保证次同步振荡为正向阻尼，实现抑制控制效果，加强风电并网的的实时性能。因此，将双馈风电机组的转速偏差作为多目标深度学习的输入约束量，经过隐含层的控制连接，完成对应的滤波平衡，当转速变化在d、q轴上产生电压变化时，则可以直接添加到原始的参考电压中，实时进行阻尼控制。

设定风电机组的转速变化量rωΔ ，在d、q轴上转子侧完成控制过程中，产生的电压变化情况如下：

式中：

ΔVd、ΔVq—d、q轴上的转子侧控制变化过程中的电压变化量；

Vd r、Vqr—附加阻尼条件下的电压变化情况；

Gd r、Gqr—d、q轴上的阻尼分量；

Δφr—隐含层的变化分量。

利用d、q轴上的附加转矩ΔTerd和ΔTerq可以实时改变阻尼，达到控制振荡的效果。

4 实验验证分析

4.1 实验环境

为了验证出本文方法下双馈风电机组次同步振荡控制方法是否有效，进行测试实验。实验中设定基础频率为500 Hz，并在串联补偿中设定40 %的振荡源，风电机组的串联补偿电容值设为35 uF，并在实验的第8 s 发出振荡源，文中研究的控制方法实时出发在转子处。次同步振荡的振源：发电设备（如发电机齿谐波（900～1 500）Hz）、输配电系统用电设备（如晶闸管整流设备）存在宽频带谐波源；共振点：网架与风电并网系统构成的容感回路有固定的振荡频率。次同步振荡种类为欠阻尼。本文设计的控制方法依托DSP 芯片，本文方法下的振荡抑制电路如图2 所示。

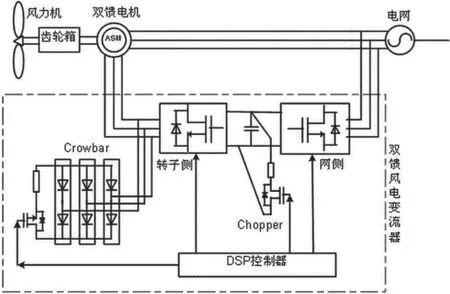
图2 本文方法下设计的次同步振荡抑制电路

在未投入任何控制措施下的双馈风电机组次同步振荡情况如图3 中的波形所示。根据图3 中放大后的波形可以看出，次同步振荡发生在第8 s 的时候，经过1 s 之后，第9 s 后波形开始严重失稳。

图3 双馈风电机组的次同步振荡情况

4.2 实验微观指标

在双馈风电机组的次同步振荡控制中，较高的阻尼比可以表述抑制振荡的有效性，并加速系统回到稳态，降低振荡幅值和频率。表达式为：

式中：

ΔVd、ΔVq—阻尼系数；

Vd r、Vqr—双馈风电机组转动惯量；

Gd r、Gqr—双馈风电机组的刚度。

4.3 实验结果对比分析

在40 %的双馈风电机组串联补偿度下，可以证明附加阻尼对次同步振荡控制是有效的。接下来为进一步测试设计方法的实用性，采用文献[1]方法、文献[2]方法作为对比方法，则三种方法的控制结果如图4 所示。

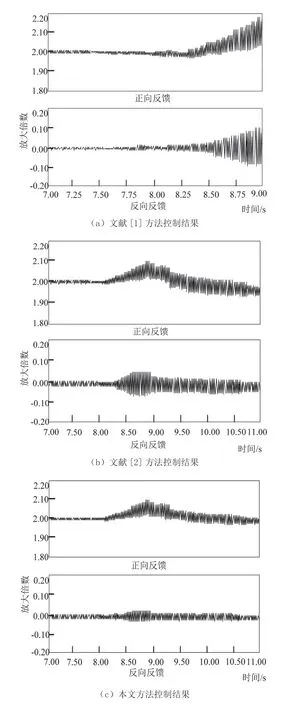
图4 不同方法控制结果对比

对双馈风电机组的次同步振荡投入控制策略，根据图4 中的实验结果表明，设计方法能够有效降低次同步振荡的波动，而对比方法控制后的次同步振荡波动仍较大，说明设计方法的控制效果较好，具有实用性。

为进一步验证设计方法的控制效果，以阻尼比为实验指标进行对比测试，测试结果如图5 所示。

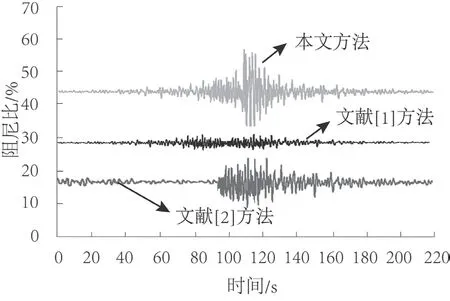
图5 不同方法阻尼比

根据图4 可以看出，本文方法的阻尼比明显高于对比方法，最高时达到43.2 %，而文献[1]方法的阻尼比最高达到了28.4 %，文献[2]方法的阻尼比最高达到了18.7 %。由此可见本文方法的次同步振荡控制效果较好。

为验证设计方法的实效性，进行次同步振荡控制时间测试，测试结果如表2 所示。

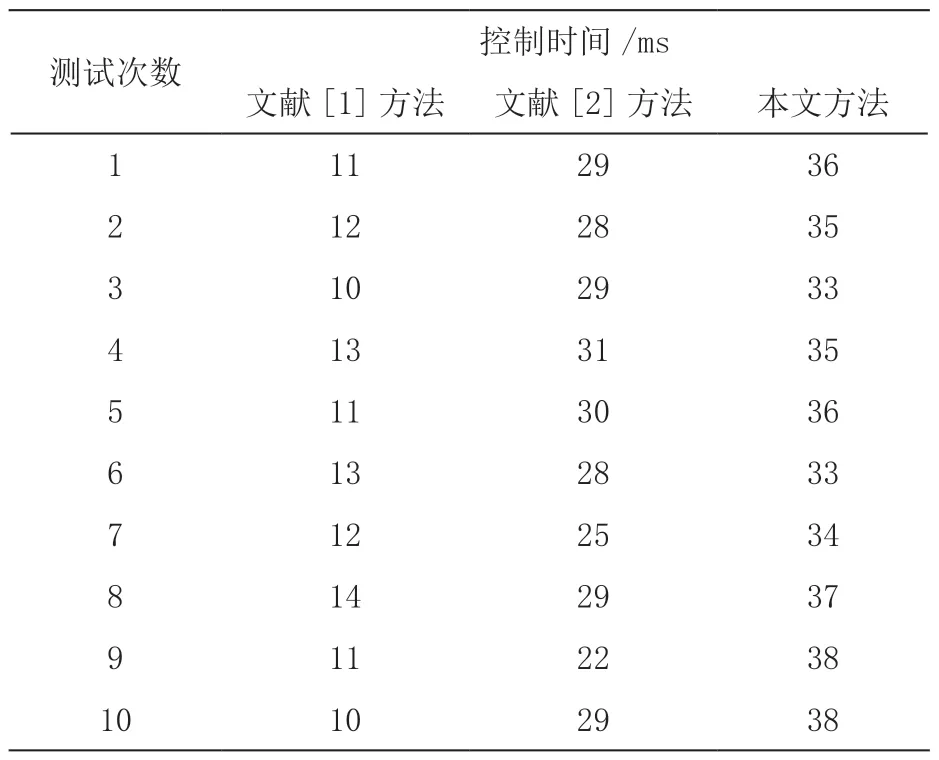
表2 测试结果

根据表2 可以看出，本文方法的次同步振荡控制时间最高为14 ms；而对比方法的次同步振荡控制时间明显高于本文方法，文献[1]方法的次同步振荡控制时间最高达到了31 ms，文献[2]方法的次同步振荡控制时间最高达到了38 ms。由此可见，本文方法的控制效率较高，具有实用性。

5 结论

为提高双馈风电机组在风电并网中的适应能力，提高并网性能，减少风电机组受到的次同步振荡影响，在研究次同步振荡控制方法的过程中，通过分析双馈风电机次同步振荡机理，进行次同步振荡特征分析，基于多目标深度学习，构建输入层、隐含层和输出层，实现对次同步振荡的特征提取和分析，实现迭代控制。实验中验证了投入控制策略的最佳时间，也证明通过控制附加阻尼能有效地实现次同步振荡的控制。