晰错因 明本质 悟方法

陶来舟 吴 跃

安徽省宿城第一中学

荆岫之玉必含纤瑕,骊龙之珠亦有微纇.一道正确(优美)的题目可以让人赏心悦目,一道错误(瑕疵)的题目同样可以令人遐想万千.本文中笔者以一道错题为例,晰错因、明本质、悟方法.

1 原题呈现

本题是华大新高考联盟2023届高三下学期4月教学质量测评(新教材卷)第8题.试题以指数复合函数和余弦函数构造的新函数为载体,考查利用导数研究函数的单调性和恒成立问题,考查学生的逻辑推理和数学运算核心素养.

下面是命题组提供的参考答案:

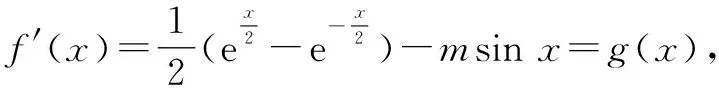
2 晰错因,以往鉴来

2.1 错因分析

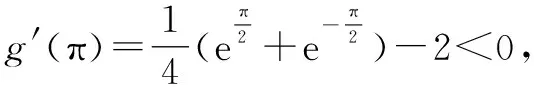
2.2 答案探究

2.3 题目修正

此题只需稍加修正,便可物尽其用,回归命题初衷,起到单选题的把关作用,不失为一道难得的好题.

此题答案为选项D,解答过程参考例1,此处省略.

3 明本质,追根溯源

定理(连续函数的局部保号性)设函数f(x)在点x0连续且f(x0)>0(或f(x0)<0),则存在x0的邻域U,对于任意给定的x∈U,有f(x)>0(或f(x)<0)[1].

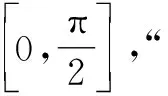
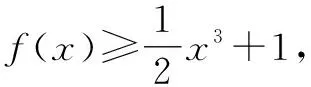
例4(2022年新高考全国Ⅱ卷节选)已知函数f(x)=xeax-ex,当x>0时,f(x)<-1,求a的取值范围.

例3用“端点效应”得到的范围是必要不充分条件(解答略),例4用“端点效应”得到的范围是充要条件(解答略).通过以上分析不难发现,“端点效应”只能给解题提供一个大致的思考方向,得到一个必要条件,然后再结合证明判断是否为充要条件.

4 悟方法,优化教学

试卷讲评是高三教学的主流形式,是发展素养的重要土壤.教学时要善于发现问题,启发学生思考并理解数学本质,引领学生真正喜欢数学.

4.1 激发学生善于思考,做示范者

《普通高中数学新课程标准(2017版2020年修订)》要求:“通过高中数学课程的学习,树立学生敢于质疑、善于思考、严谨求实的科学精神.”2021年4月,习近平总书记在清华大学考察时强调:“教师要成为“大先生”,做学生为学、为事、为人的示范,促进学生成长为全面发展的人.”[2]善于思考不能流于形式,不是教师在课堂上强调几遍就敷衍了事;善于思考也不能放手交给学生,因为学生缺少思考经验只会走入另一误区.教师应该以身作则做示范者,通过精选试题、练习和精心设计教学环节引导学生去思考.

4.2 高屋建瓴指点迷津,做指导者

高中数学试题纷繁复杂,解法灵活多变,学生的思维更是光怪陆离(天马行空).要提高教学效率,就需要教师提高个人专业水平.《中学教师专业标准》要求数学教师要以素养为依托,通过实践,掌握教学所需的基础知识,提升教书育人的基本能力.以其昏昏,使人昭昭,只会让学生越来越迷糊.以导数的教学为例,在这一模块中,存在许多易造成解题思维障碍的问题:①知识间的不等价转化,如“单调性与导函数的符号”“极值点与导函数的零点”等;②方法间的不等价转化,如“端点效应”“拉格朗日中值定理”等;③存在很多高等数学知识,如“洛必达法则”“泰勒展开式”等.这些问题在学习和解题时都会给学生带来不小的困惑,需要教师高屋建瓴指点迷津.打铁还需自身硬,教师应该自己先搞清楚,做个明白人,才能在教学中“不畏浮云遮望眼”.

4.3 引领学生学会学习,做引路者

高三教学因为教学任务重、教学时间紧,很多都是“满堂灌”,笔者有时也不得已而为之.“满堂灌”的教学方式看似完成了教学任务,实际教学效果却不佳,教师课后的心满意足、“扬扬得意”也只是一种自我慰藉而已.讲过的题目学生仍然不会,这种情况屡见不鲜,究其原因就是学生是被动的“接受者”,课堂上看似学习了很多,但真正“动手操作”的太少.因此,教师要做学生学会学习的引路者,引领学生变被动为主动,在教学中践行“一题一课”“深度学习”等新的教学理念,让课堂“慢下来”,让效率“提上去”.