结合注意力机制的BiLSTM电力负荷预测

秦昊禹，董 阳，丁浩申

（1.中国民航机场建设集团，北京 101300；2.中国民航信息网络股份有限公司，北京 101318）

随着我国能源发展进入新时代，促进能源合理配置成为重要任务之一[1]。电力负荷的预测可以归结为时间序列问题，近些年，国内外学者针对时间序列模型的研究和应用非常广泛，相关内容大致可分为三类。第一类是基于统计学模型的预测方法，其中比较常见的是积分整合移动平均自回归（Autoregressive Integrated Moving Average，ARIMA）模型及其变体[2-3]。该类方法的优势在于其可解释性较强，且在建模时不需要大量数据，但很难应对随机性较强且具有非线性变化特点的短期电力负荷数据。第二类是浅层机器学习类算法。浅层机器学习方法中的代表是支持向量回归（Support Vector Regression，SVR）算法[4-5]，该类方法使用浅层的神经网络，尽管可以在一定程度上应对数据的非线性变化，但依然难以准确学习复杂的数据特征。第三类是近年来快速发展的深度学习类的方法[6-7]，相比而言，选择深度学习类方法进行预测时，能够通过深层的神经网络模型实现更复杂的非线性变化，实现更精准的预测。因此，本文提出一种融合注意力机制（Attention Mechanism）的BiLSTM-Attention模型，以提高模型对非线性数据的特征提取能力。

1 模型基本原理

模型的结构如图1所示。

图1 模型结构图

2 数据处理及评价标准

2.1 数据处理

本文所用数据选自某地区2009年1月1日—2015年1月8日的电力负荷数值。在数据处理方面，首先将数据按照7个步长（每个步长为1天）进行切片，得到维度的张量作为输入数据。将输入数据分为训练集和测试集，其中，训练集共2 000条，测试集193条。

为了提升模型的训练效果，减少数据波动较大产生的影响，本文采用z-score标准化的数据处理方法，具体公式如下：

2.2 评价标准

本文的评价标准采用平均绝对误差（Mean Absolute Error，MAE）、均方根差（Root Mean Square Error，RMSE）和平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）。三种误差指标的计算方法如式（5）所示：

RMSE误差计算方法如式（6）所示：

MAPE误差计算方法如式（7）所示：

3 实验分析

本文选取了3种基准方法进行对比，对比的评价标准包括MAE、RMSE和MAPE，得到结果如表1所示。

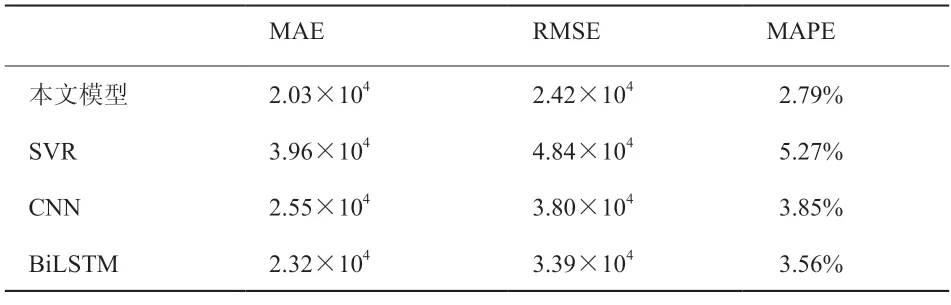
表1 实验结果对比

由表1可以看出，本文提出的模型MAE、RMSE和MAPE误差均优于对比的模型。

最终的电力负荷预测结果如图2所示，可以看出，本文提出的模型与真实值更为接近，尤其在数据波动较大的情况下，本文提出的模型能够更好地预测变化趋势。

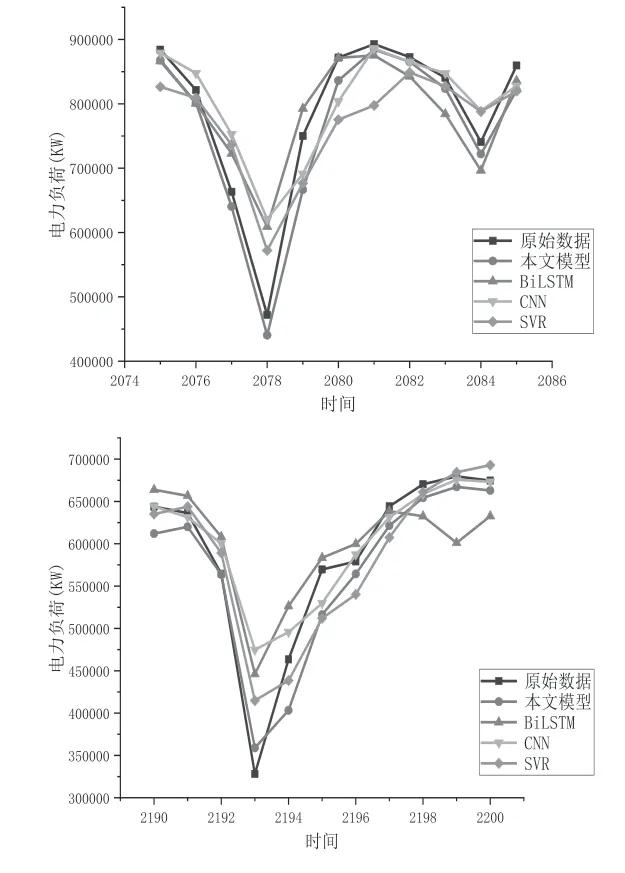
图2 电力负荷预测结果对比图

4 结束语

本文针对电力负荷预测中，以往方法存在关键特征提取能力不强导致的精度不足问题进行研究，在BiLSTM模型的基础上，增加了注意力机制，构建了BiLSTM-Attention模型，增强了模型的特征提取能力。实验结果表明，在面对电力负荷出现多次波动的情况下，本文所设计的预测模型依然能够达到更精确的预测效果。与几种常规的时间序列预测模型进行对比，本文提出的模型误差更小，更加接近真实值。