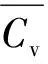格式塔原则下的建筑群空间分布智能理解

张凯业, 汪 逸, 梁勤欧

(浙江师范大学 地理与环境科学学院,浙江 金华 321004)

0 前 言

建筑群的空间分布特征是指多个建筑物在地理空间分布中的形状特征或排列方式,是进行地理空间数据多尺度表达及地图自动综合等的关键因素.因此,让计算机像人脑一样智能理解建筑群的空间分布特征,是地理空间认知领域值得重点关注的问题[1-2].当人们处于空间认知方式时,格式塔原则由于重视视觉认知过程中物体结构的整体性,它既符合人类对地理空间分布的认知,又能让计算机较完整地表达出隐含于建筑群中的空间信息,其在中大比例尺地图自动综合中有着较为广泛的应用[3-4].

在格式塔原则约束下对建筑群聚类是挖掘建筑群空间分布特征、实现建筑群自动综合的首要条件.有许多研究对建筑群的聚类分析方法进行了深入探讨,如在层次聚类方面,刘慧敏等[5]、艾廷华等[6]利用建筑物加密点的Delaunay三角网描述建筑物之间的通视区域,并通过三角网的骨架线和最小生成树(minimum spanning tree,MST)对建筑群进行聚类.在MST基础上,Qi等[7]提出逐个加入建筑物的面积、密度等格式塔因子对建筑群进行分级约束,并根据各个影响因子的重要性,利用MST实现了建筑群的分层聚类.孙前虎[8]通过MST对比建筑物间的质心距离、最近距离、旋转卡壳平均距离等值,并结合方向性和邻近性等探讨了建筑物之间的不同距离约束对建筑群聚类的影响.王安东[9]、Zhang等[10-11]利用建筑物的MST连接边,通过跟踪算法实现了建筑群线性和非线性排列模式的识别,充分表达了建筑物的几何特征和空间分布特征,为聚类后的建筑群进行自动综合奠定了基础.在密度聚类方面,刘呈熠等[12]引入新的面要素分布密度参数——聚集度,利用聚集度识别聚类中心得到初始的面群,并通过建立的边缘检测和群组合并模型,得到空间邻近面的主次关系,从而实现聚类.在划分聚类方面,王真[13]、程博艳等[14]利用SOM(self organizing maps)竞争神经网络对建筑群进行初步聚类,并在格式塔原则的约束下,通过行列扫描法和建筑物之间的因子特征相似性对建筑群进行了二次精细聚类.另外,高晓蓉等[15]、杨俊等[16]基于空间相似性理论提出居民地、土地利用图斑等面实体在多尺度空间中的语义相似度计算模型,为大比例尺下建筑群的聚类与地图自动综合提供借鉴.

上述方法都充分考虑了建筑物自身的几何形态特征和建筑群的空间分布特征,其中MST由于自身只需要设定少量参数便能达到聚类目的,在空间聚类中被广泛应用.相关文献研究大都选用集中均匀排列的城区建筑群(类似图1(a)),并设定合理阈值去对MST进行剪枝、聚类,但都缺乏利用固定阈值对分散均匀排列的城区建筑群(类似图1(b))的聚类讨论.而阈值的设定往往具有较强的人工干预性.因为MST聚类不同于地图自动综合,若点与点、线与线或面与面之间的距离小于地形图图式标准规范的距离,便对目标进行相应的综合操作.相反,MST剪枝边的权值并没有一个固定的标准,需要人为指定.若阈值指定合理,则能提高计算机对建筑群聚类和自动综合的质量,改善人们对地图的认知.但是合理的阈值往往需要大量的人工试验,这并不符合计算机智能化处理的规定.为此,Zahn[17]提出了一种参数检测方法,其不需要指定阈值就能对MST边进行剪枝,但是Zahn只是从算法的角度介绍各个参数设置的合理性,并没有将该方法应用到具有地理空间分布特征的建筑群中去,后续也没有相关的研究将MST参数检测与MST阈值方法进行定量的比较.

(a)集中均匀排列城区建筑群

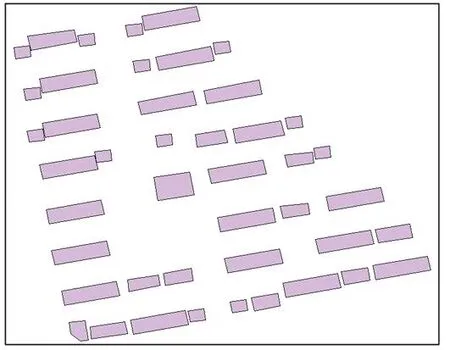
(b)分散均匀排列城区建筑群

因此,本文围绕MST和格式塔原则下的建筑群空间分布智能理解这一主题,期待解决以下2个问题：1)对于分散均匀排列的城区建筑群来说,MST通过固定阈值聚类是否能像集中均匀排列的城区一样维持建筑群的空间分布特征?若不能,原因是什么?2)MST参数聚类和阈值聚类的适应性问题.

1 建筑群空间分布特征挖掘方法

1.1 格式塔约束下建筑物的空间邻近关系及视觉距离表达

如何将格式塔这一心理学原则用于定量描述建筑物之间的特征差异?在描述这种差异之前,需先挖掘建筑物的邻近关系.Delaunay三角网具备的“外接圆规则”和“最邻近连接”特征是空间邻近分析的有力工具[18].因此,本文利用Delaunay三角网将格式塔原则邻近性质对应建筑物间的邻近关系,相似性对应邻近建筑物间的面积差异、形状差异、密度差异,同向性对应方向差异.差异越大,则邻近建筑物视觉距离越大,越不符合格式塔原则,越不能被视为一类.因此,可以将建筑物之间的特征差异问题定量为视觉距离大小问题,具体计算视觉距离的步骤如下：

首先,利用建筑物边界内插生成的加密点构建Delaunay三角网,若建筑物边界与三角形其中一个边界重合,则两建筑物空间邻近,生成邻近矩阵,连接2个建筑物的质心生成无加权值、不受约束的邻近边.其次,参考文献[6]的骨架线连接方法,对连接之后的每条骨架线赋予通视区域,并进行邻近距离的计算,得到加权、不受约束的邻近边.同时,选取建筑物的面积、密度、形状、方向作为格式塔因子来约束邻近边,其对应于格式塔原则的相似性和同向性.表1为各个参数的计算方法.

表1 视觉距离的定量化参数

之后利用式(1)～式(4)对邻近边进行格式塔约束获得加权、受约束的邻近边.

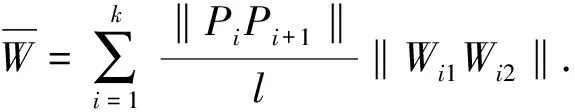
(1)

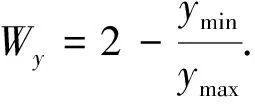
(2)

式(2)中：ymin和ymax分别表示2个邻近建筑物之间最小和最大的面积、密度、形状;Wy表示各因子对应的权重.

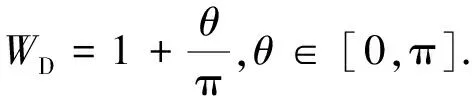
(3)

式(3)中：θ表示建筑物之间的SMBR方向夹角.WD表示方向因子对应的权重.

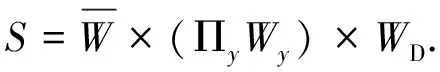
(4)

式(4)中,S表示视觉距离.最后利用Prim算法在空间邻近图的基础上构建MST,此时MST的权值为视觉距离S.如图2(d)所示,虽然计算得到115—155和137—155的邻近距离相当,但是经过格式塔的面积约束,115—155的视觉距离要大于137—155的视觉距离(3个绿色建筑所示).

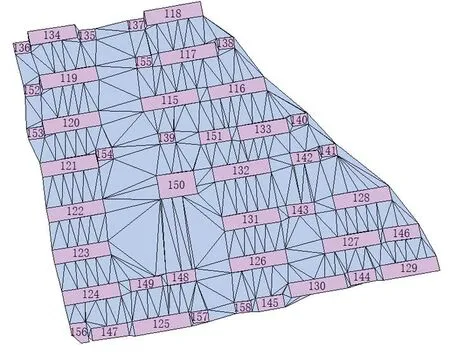
(a)Delaunay三角网

(b)骨架线(红线)

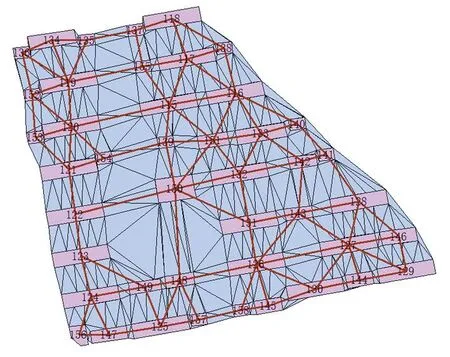
(c)空间邻近图

(d)MST图

1.2 顾及建筑群空间分布的MST参数聚类

最小生成树(MST)是包含原图n个顶点的极小连通子图(图2(d)所示),通过自身的结构特点在空间聚类方面得到广泛应用,它并不用事先预定聚类的数目,而是只通过对边的剪枝达到聚类的目的.大部分剪枝方法都是通过设定一定的阈值,若边的权值大于该阈值,则剪枝该边,Zahn称剪枝边为不一致边.而MST边的阈值剪枝仅仅考虑单条边的权值,忽略了在一定范围内与该边具有相似几何和空间特征的建筑群之间边的关系,即没有考虑建筑群的空间分布特征.为此,Zahn提出一种检测不一致边的方法,即利用参数检测,其定义如下：

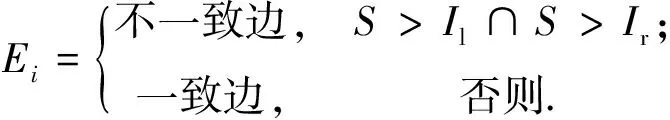
(5)

式(5)中,Il和Ir分别表示左邻近边综合权值和右邻近边综合权值,综合权值为

I=max{f×Smean,Smean+n×Sstd}.

(6)

式(6)中：Smean表示左或右二阶邻近边权值的平均值;Sstd表示左或右二阶邻近边权值的标准差,若左或右不存在第2阶邻近边,则只判断右或左的二阶邻近边;f和n为自定义参数,由前人的研究结果可知,f≥1,n≥3对不一致边的检测有意义,具体原因可查看文献[9].不一致边检测算法如下：

步骤1：将f设为1到2,步长为0.1,将n设为3～4,步长为0.1,即共有121种不同的参数组合.

步骤2：准备A,B,C,D4个列表,A,B列表分别用来存储左、右邻近边权值,C,D列表用来存储检测边的ID码,并将该边标为已访问状态.同时提取检测边两端顶点的ID码作为变量.令L1为A|B列表中元素的个数,L2为C|D列表中元素的个数.

步骤3：在全局范围内搜索未访问的并与一端顶点ID码重合的边,将权值写入A列表中,将边的ID码写入C列表,并将提取的邻近边标为已访问状态.计算L1.

步骤4：遍历C列表,并重复步骤2和3直至所有边都被标为已访问状态.计算L2.若L1=L2,则不存在第2阶邻近边,将A列表及C列表清空.

步骤5：在全局范围内搜索未访问的并与另一端顶点ID码重合的边,将权值写入B列表中,将边的ID码写入D列表,并将提取的邻近边标为已访问状态.计算L1.

步骤6：遍历D列表,并将已遍历的边标为已访问状态,并重复步骤2和步骤3直至所有边都被标为已访问状态.计算L2.若L1=L2,则不存在第2阶邻近边,将B列表及D列表清空.

步骤7：分别对A,B列表计算Il和Ir,并利用式(5)～式(6)判断MST中的不一致边,若是不一致边,则标为False.之后转至步骤2～步骤7,并清空A,B,C这3个列表,将所有边都标为未访问状态.当所有边都判断完毕后,将False边删除,转至步骤1～步骤7.重新调整参数直至所有的参数组合计算完毕.

1.3 建筑群空间分布特征的挖掘质量评价

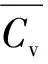
1.4 建筑物语义相似度

建筑物的语义特征在建筑物聚类或者是地图自动综合中起着重要作用.为此,本文先利用建筑物的几何形态特征和空间分布特征,再利用语义特征对建筑群进行二次聚类,通过二次聚类的结果来表达更符合人类认知的建筑群空间分布.在一般的地图数据库中,建筑物语义特征很难获取,而通过高德地图获取POI数据是目前获取建筑物语义特征效率最高的一种方式[20].虽然提取的POI数据能准确描述建筑物的语义信息,但是并不是所有的POI数据点都会落在建筑物内,因此,需要对建筑物进行一定距离的缓冲来覆盖POI数据点,若是建筑物的缓冲区没有覆盖POI数据点,则默认建筑物的语义特征与最邻近建筑物相同.

由于POI数据类别的多样性,高德地图对POI数据进行了分类编码,本文根据试验区域将POI划分为相应的语义类型.然而这些文本类的属性信息并不像建筑物的面积、方向那样能直接进行定量化的描述和比较.为此,文献[5]在语义信息的基础上定义了建筑物的语义向量等指标,其定义为：

1)建筑物语义向量：假设研究区存在N类数据点,那么任意的建筑物bi的语义类型可以通过一个N维向量进行描述,表达为

Fi=(r1,r2,r3,…,rk,…,rN).

(7)

式(7)中,rk为落入bi的第k类数据点的数目与第k类数据点总数的比值.本文中N=7.

2)建筑物语义相似度：通过2个建筑物(bi和bj)的功能向量Fi,采用向量余弦来描述2个建筑物之间的语义相似度Fsim,表达为

(8)

式(8)中：|Fi|和|Fj|为功能向量的模;Fi·Fj为功能向量的内积.

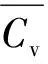
2 试验分析

2.1 试验数据来源

试验区域分别是金华市城区部分分散均匀排列建筑群,美国迈阿密城区部分集中均匀排列建筑群.建筑群矢量数据来源于OSM(open street map,开源平台),前者共包含849个建筑,后者包含395个建筑,比例尺都为1∶6 500.如图3所示.

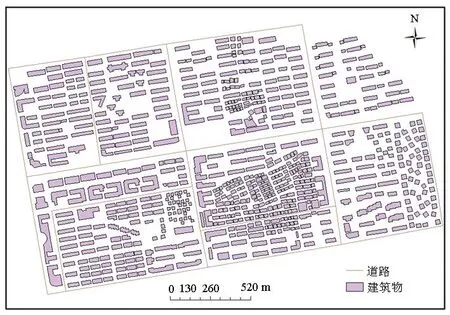
(a)金华市部分分散均匀排列建筑群

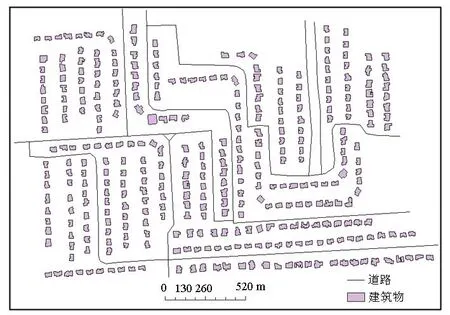
(b)迈阿密部分集中均匀排列建筑群

2.2 试验结果分析

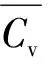
(a)最优参数聚类

(b)阈值聚类

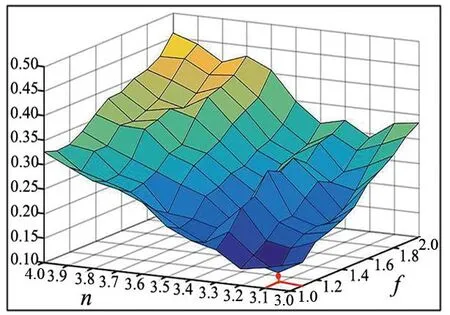
(c)参数聚类值

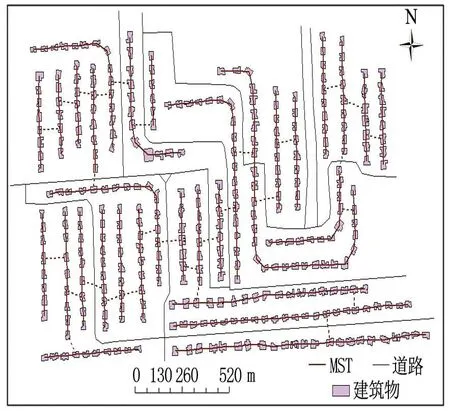
(d)集中均匀排列建筑群聚类结果

(e)最优参数聚类部分区域放大

1)图4(e)中的虚线(ABCDFGH虚线)表示在阈值聚类中被视为不一致边,而在参数聚类中被视为一致边的线.对1区建筑进行参数聚类时,发现建筑群大致呈线性排列,MST边没有被剪枝,可以将这一列建筑群归为一类;若使用阈值聚类,会发现ABCD边由于大于设定的阈值而被剪枝,导致建筑群的空间分布特征被破坏.出现此情况是因为在参数聚类时由于邻近边的存在,会提高式(5)中Il或Ir的值,导致其不容易符合式(5)不一致边的识别条件.

2)对2区建筑进行聚类时,由于F边连接的2个建筑面积及形状的差异大,其视觉距离也增大,从而被阈值聚类和参数聚类同时视为不一致边,维持了2区上方的8个建筑和下方的7个建筑的线性排列,符合格式塔原则.但是E边和G边在阈值聚类中却被视为不一致边,使得建筑群空间分布特征被破坏.原因是,虽然E,G两边的权值大于阈值,但是由于F边的存在,利用参数聚类对E,G两边进行不一致边检测时会提高式(5)中Il或Ir的值,导致其不易符合式(5)不一致边的识别条件.

3)由于3区建筑群的整体排列结构相对整齐,符合文献[21]提到的组合直线模式,因此,3区建筑群往往会被归为一类.但是由于面积、密度差异及邻近距离较大,H边所连接的两建筑物的视觉距离权值会大于其余边的权值,进而在阈值聚类时,H边下方的2个建筑被单独分成了一类.经计算发现,H边的视觉距离为29.146 m,恰好大于27 m的阈值,而在参数聚类中H边的Il为31.913 m,不符合不一致边识别条件.

图4(d)为集中均匀排列建筑群的MST,其利用参数聚类和阈值聚类挖掘建筑群空间分布特征.经试验发现,二者挖掘出的建筑群空间分布特征结果一致,并能很好地展现建筑群线性排列的空间分布特征,符合人类的视觉认知.虚线表示检测出的不一致边.

经过试验分析可以得出,MST的参数聚类不仅适用于集中均匀排列建筑群,且适用于分散均匀排列建筑群,而传统MST的阈值聚类仅仅适用于集中均匀排列建筑群.

2.3 试验原因讨论

1)集中均匀排列建筑群由于排列整齐,同一簇建筑群之间邻近距离小,视觉距离小,变化小,说明簇内Cv值较小.而不同簇之间的建筑群,即图5中MST虚线(不一致边),其邻近距离大,视觉距离权值大,明显大于簇内的视觉平均距离,这使得阈值较容易确定,很少出现在经过格式塔约束后,簇内建筑物视觉距离大于簇间建筑物视觉距离的情况.

2)簇间建筑物视觉距离往往会大于簇内建筑物视觉的平均距离.对于分散均匀排列建筑群,由于簇与簇之间的邻近距离小,簇间建筑物视觉距离与簇内建筑物视觉平均距离的差异会小于集中均匀排列建筑群的差异,并且同一簇内建筑物虽然邻近距离小,但建筑物面积等变化大,视觉距离变化大,说明簇内Cv值较大.这使得阈值不容易确定,导致同一簇内部分建筑物视觉距离大于阈值,如图4(e)的3个区域所示.

2.4 POI二次聚类

利用参数聚类后的建筑群进行POI二次聚类.根据金华市城区部分建筑,将POI数据划分为7种语义类型(具体见图例).语义相似度阈值β1=0.7,建筑缓冲距离设置为5 m,得到二次聚类结果,具体如图5所示.

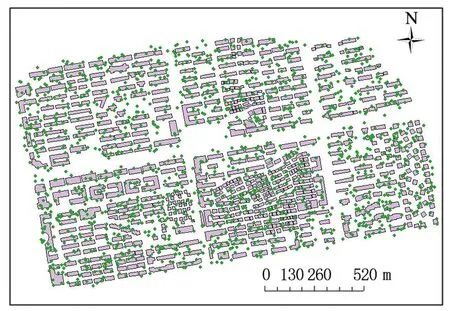
(a)POI数据点

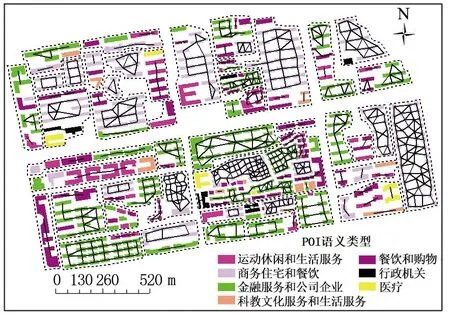
(b)POI二次聚类

3 结 语

实现建筑群自动地图综合首先要挖掘出建筑群的空间分布特征,建筑群聚类是挖掘建筑群空间分布特征的基础.