基于图框架变换的动态图神经网络模型

杨圣鹏, 施建栋, 周斯炜, 李 明

(1.浙江师范大学 计算机科学与技术学院,浙江 金华 321004;2.浙江师范大学 浙江省智能教育技术与应用重点实验室,浙江 金华 321004)

0 引 言

自基于深度学习的数据分析方法在学术界取得系列成果以来,已经有大量的模型应用深度学习技术对各类数据进行分析和处理,并在多个领域取得了广泛的应用.然而,目前大部分的模型仅适用于处理欧氏空间的网格型数据.Kipf等[1]指出,由于非欧结构的图数据不具备欧氏空间中的规则性和均匀性,所以传统的卷积操作无法直接应用于图数据的特征提取;Bruna等[2]指出,由于图数据的频谱特性和传统信号处理中的频谱特性存在差异,所以欧氏空间中的频域处理方法也无法直接应用于非欧结构的图数据;Hamilton等[3]也明确了由于非欧结构的图数据具有复杂的连接关系和异构节点属性,传统的特征聚合方法无法充分捕捉到图数据的全局结构和节点之间的复杂交互.而在数据表现形式繁多的大数据时代,非欧结构图数据的应用背景又非常广泛.例如,在社交网络分析领域,通过分析社交网络中的节点和边的连接模式,可以揭示社会关系、社交影响力、社区发现等信息,从而实现更精准的个性化推荐和媒体营销[4].在交通网络规划中,通过分析交通网络中节点和边的连接关系,可以进行路径规划、交通流量预测等工作,有助于改善交通运输系统[5].此外,图数据还在知识图谱、网络安全、推荐系统等领域得到了广泛的应用,通过构建和分析图数据,能够从复杂的关系中发现隐藏的模式和知识,从而实现智能搜索、语义理解、智能推荐等功能[6].欧氏空间网格型数据与非欧空间图结构数据特征如图1所示.

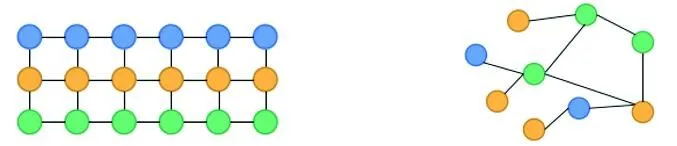
(a)欧氏空间网格型数据 (b)非欧空间图结构数据

动态图是非欧空间图结构数据中一类特殊的数据形式,具有丰富的时间和空间演变特征.在以往的研究中,Wang等[7]提出了通过聚合邻居节点特征来更新中心节点表示的动态图卷积模型,并与传统的静态图卷积模型在分类任务和分割任务上进行了实验对比,发现用图卷积网络等静态图模型对动态图进行表示学习会导致信息丢失,使实验结果变差;Manessi等[8]在静态图中引入时间维度,将静态图扩展为动态图并提出了用邻居节点信息和时间维度的变化更新节点特征的动态图卷积模型,分别完成了图分类和图预测任务,发现静态图卷积模型无法处理动态图数据中节点的新增、删除和连接关系的变化,无法直接对动态图数据的时空演变进行建模;Pareja等[9]提出了将RNN[10]和GCN[11]结合使用的动态图表示学习方法,并指出因为静态图模型无法自适应地学习图结构和特征随时间变化时的演变特征,所以静态图表示学习方法在动态图中并不适用.因此,动态图表示学习领域吸引了众多研究者的关注,提出了各种方法来处理这种动态图数据.例如,Sankar等[12]在动态图表示学习中引入注意力机制,构建不同时间下图演变的时间和空间信息;Liu等[13]在RNN[10]和GCN[11]之中引入Z核结构,进一步考虑了动态图单个时间戳中的同一局部不同细粒度的相似信息,提高了后续任务的效果;Yu等[14]通过深层自编码器和图距离游走方式对动态图进行重新编码,实时更新节点状态并进行图聚类分析;Liu等[15]综合考虑动态图神经网络在同一时刻的全局信息、局部信息和动态演变信息,在多个动态图异常检测基准数据集上取得了最佳效果.

基于上述处理欧氏结构的特征提取方式并不适用于非欧结构,且静态图表示学习模型也无法准确捕获动态图中的时空演变特征的论述,本文提出一种针对动态图表示学习的模型,主要创新和贡献总结如下：

1)将动态图表示学习与非欧空间图框架理论结合起来,提出了一种基于图变换框架的动态图神经网络模型,进一步拓展基于谱方法的动态图表示学习技术;

2)通过兼顾低通滤波器和高通滤波器,所提模型能够有效地挖掘动态图的低频、高频信息及其演变模式,提升了动态图神经网络的表达能力;

3)所提模型在3个动态图公共基准数据集上的精度优于已有动态图表示学习算法,验证了基于图框架变换的动态图神经网络模型的潜在优势.

1 动态图与动态图表示学习的定义

1.1 动态图

根据数据的时序处理角度可以把动态图划分为两大类：一类是在固定的时间戳中记录图数据,称为离散动态图,如图2(a)所示;另一类是记录连续时间下的图数据,称为连续动态图,如图2(b)所示.

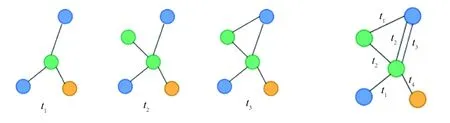
(a)离散动态图 (b)连续动态图

本文基于离散动态图结构,根据离散动态图中顶点和边的动态特性进一步把它划分为如下3类图形.

第1类：图3表示带有动态特征的静态图结构,它是图矩阵G和节点特征矩阵X的有序集合D={(G,X1),(G,X2),…,(G,XT)},其中节点特征矩阵满足Xt∈R|V|×d,∀t∈{1,2,…,T}为时间序列中单个时间戳,V={v1,v2,v3,…},vi(i=1,2,…)为节点,|V|表示节点数量,d表示特征维度.即在该类动态图中,节点特征随着时间的流逝而发生改变,图形的结构在各个时刻中均不发生改变.

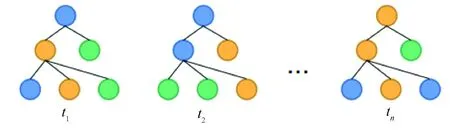
图3 特征演变的动态图结构

第2类：图4表示带有静态特征的动态图结构,它是图矩阵和节点特征矩阵的有序集合D={(G1,X),(G2,X),…,(GT,X)},其中Gt为t时刻的图矩阵,节点集合满足Vt=V,∀t∈{1,2,…,T},节点特征矩阵满足X∈R|V|×d.即在该类动态图中,节点特征在各个时刻中均不发生改变,图形的结构随着时间的流逝而发生改变.

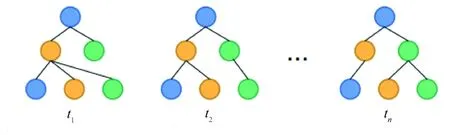
图4 图结构演变的动态图

第3类：图5表示带有动态特征的动态图结构,它是图矩阵和节点特征矩阵的有序集合D={(G1,X1),(G2,X2),…,(GT,XT)},其中节点集合满足Vt=V,∀t∈{1,2,…,T},节点特征矩阵满足Xt∈R|V|×d,∀t∈{1,2,…,T}.即在该类动态图中,节点特征和图形结构在不同时刻均发生改变.

图5 特征及结构同时演变的动态图

1.2 动态图表示学习

动态图表示学习是指从动态图数据中学习节点和边嵌入的任务.给定动态图=(V,E,T)作为模型输入,其中E表示边集合,然后用神经网络的方法设计一个函数F表示可以映射节点和边特征的模型,使得在具体的时间戳t下,动态图中每个节点v∈V和边e∈E,有hv(t)=F(v,t),he(t)=F(e,t)分别对节点v和边e进行嵌入,旨在捕捉动态图中节点和边在时空演变过程中的关联性和变化模式,为后续的图分析、预测和推荐等任务提供有意义的指导.

2 基于图框架变换的动态图神经网络模型

目前大部分的图神经网络都是基于空间建模的,如GCN[11],GAT[16]等,这些方法通过空间消息传递的方式计算邻居节点的信息,并通过图卷积技术将源节点和目标节点的信息汇聚整合,经过多层网络堆叠训练,最终实现全图特征学习.然而,这些基于空域建模的方法存在一些局限性,浅层图卷积技术无法有效传播节点标签,而深层图卷积堆叠会导致特征过度平滑,难以区分不同类别的节点[6,11].另一种建模方法是通过傅里叶变换把信号传入谱域,先将空域信号投影到傅里叶基上,以此确定信号在谱图中的幅值大小,进行系列操作后再通过逆傅里叶变换无差别地将信号传回空域,这种基于谱域的数据分析和建模方法对于频率随着时间发生改变的非平稳信号有着很大的局限性[17].

为了弥补基于空域和谱域建模的缺陷,考虑到小波变换比较适用于处理非平稳过程的信号特点,决定引入小波变换.在现有的研究中,Xu等[18]在传统的图卷积神经网络基础上引入了小波变换,在不同的频率尺度上提取图结构和特征信息,从而实现更全面的图表示学习,但模型整体结构注重局部邻域的信息,对全局图结构表示相对较弱,这导致在一些全局性图任务学习或者具有长程依赖关系的图数据上性能受限.Zheng等[19]提出了用小波图框架来增强图神经网络的性能,将信号分解为不同的频域子空间来更好地表示信号的细节和整体特征,从而提高图神经网络对于图结构的特征提取能力,该模型只考虑了静态图结构,并没有进一步将小波变换用于动态图结构中.本文受此启发,首先将空域信号投影到小波基上,然后对低频信号和高频信号有区分地进行滤波操作,并在谱空间设计激活函数进行信号压缩和去噪,从而构建了一个针对动态图信号提取的谱域卷积模型,再用整个卷积模块替换长短期记忆神经网络中的乘积操作,利用长短期神经网络能够学习数据中长程依赖关系的特性,捕捉动态图的演变特征,构建了基于图卷积框架变换的动态图神经网络模型,即dynamic graph neural network model based on graph frameles transform(GFTLSTM),模型结构如图6所示.

2.1 基于图框架变换的多尺度图卷积

2.1.1 动态图信号转换

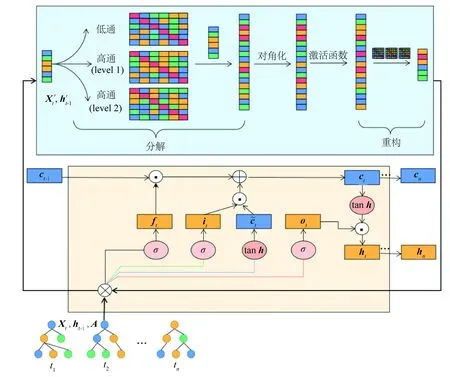
图6 基于图框架变换的动态图神经网络模型框架示意图

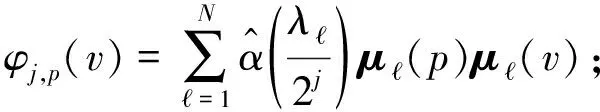
(1)

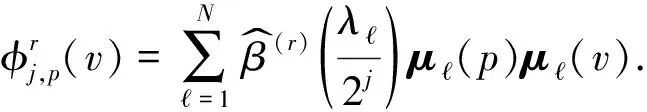
(2)

由于深度学习训练的数据是张量形式,所以式(1)和式(2)在具体实现时将傅里叶变换替换成小波变换后,对于图信号s的转换可以通过信号分解矩阵Wr,j(r=0,1,…,n)和信号重构矩阵Br,j来执行[19].由信号分解矩阵可以构成一个长度为nJ+1的矩阵集合Q,如式(3) 所示[20].

Q={Wr,j|r=1,2,…,m;j=1,2,…,J}∪{W0,J}.

(3)

2.1.2 多尺度图卷积

综合上述动态图信号转换知识,为了更好地捕获动态图演变特征,本文将t-1时刻的隐状态矩阵ht-1与当前时刻的输入特征矩阵Xt作为卷积模型的输入特征,卷积计算过程如式(4)和式(5)所示.

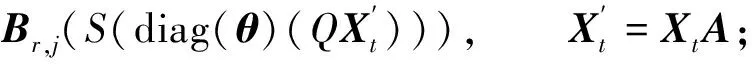
(4)

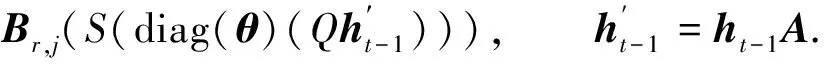
(5)

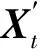
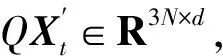
Ss(x)=sgn(x)(|x|-δ)+;

(6)

Sh(x)=x(|x|-δ).

(7)

式(6)和式(7)中：Ss和Sh分别为Shrinkage-soft和Shrinkage-hard信号压缩函数;sgn()为符号函数;x为输入特征;δ作为一个门限值,可以控制信号分量值,进一步压缩信号.

2.2 长短期记忆网络(LSTM)

长短期记忆网络(long short-term memory networks,LSTM)是循环神经网络中的一种,主要用于解决长序列训练过程中的梯度消失和梯度爆炸问题[21].本文将图卷积操作与长短期记忆神经网络相融合,将长短期记忆网络中输入矩阵Xt与上一时刻的外部状态ht-1同权重矩阵Aξ,Uξ(ξ∈{i,f,c,o})的乘积操作替换成基于图框架变换的多尺度图卷积.具体处理过程如式(8)所示.

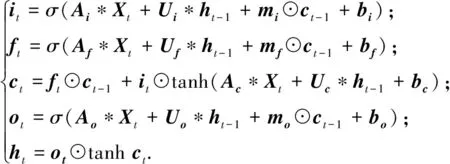
(8)

式(8)中：*表示基于图框架变换的多尺度卷积操作;bξ表示偏置矩阵;mρ(ρ∈{i,f,o})表示对角矩阵;ct-1表示上一时刻的内部状态,记录了时序中到上一时刻为止的所有历史信息;输入门it的作用是对当前输入数据进行选择性记忆,减少不重要信息的输入;遗忘门ft的作用是选择性地忘记上一时刻的内部状态信息,删除不重要的信息;ct表示当前时刻的内部状态,用于更新需要保留的信息;输出门ot的作用是控制当前时刻的内部状态ct有多少信息需要输出给外部状态ht.

3 实 验

3.1 数据集简介

1)Chickenpox Hungary[22]

匈牙利官方报告的2005—2015年匈牙利每周水痘病例动态图数据集,节点是县城,边表示县城之间的邻接关系,预测目标是下一周的患病数量.

2)Pedal Me London[22]

一个描述2020—2021年伦敦货运自行车物流公司每周交付订单量的动态图数据集,节点是地理位置单元,边描述的是节点的空间连接关系,预测目标是下一周的交货数量.

3)Wikipedia Math[22]

一个描述2019年3月到2020年3月用户每天访问维基百科次数的动态图数据集,是一个有向加权的动态图,节点是维基百科中关于数学话题的页面,边的权重表示在源维基百科链接到目标维基百科的数量,预测目标是下一天的页面访问量.

3.2 实验设置

实验在3个动态图数据集上采用如下2种不同的训练方式：

1)Incremental：动态图中的每个时序快照都会更新损失和训练权重.

2)Cumulative：动态图中的每个时序快照中的损失会被累积后再进行反向传播.

在Incremental训练方式上,采用Shrinkage-hard函数,硬性阈值特性能够将较小的权重压缩为0,减少旧数据的影响,使得模型更快地适应新的动态图变化;在Cumulative训练方式上,采用Shrinkage-soft函数,软阈值特性可以对权重进行平滑收缩,减少权重的幅度,但不将其直接压缩为0,有助于保留历史数据信息,综合考虑整个动态图的演变关联特征.本文模型中的超参数设置见表1.

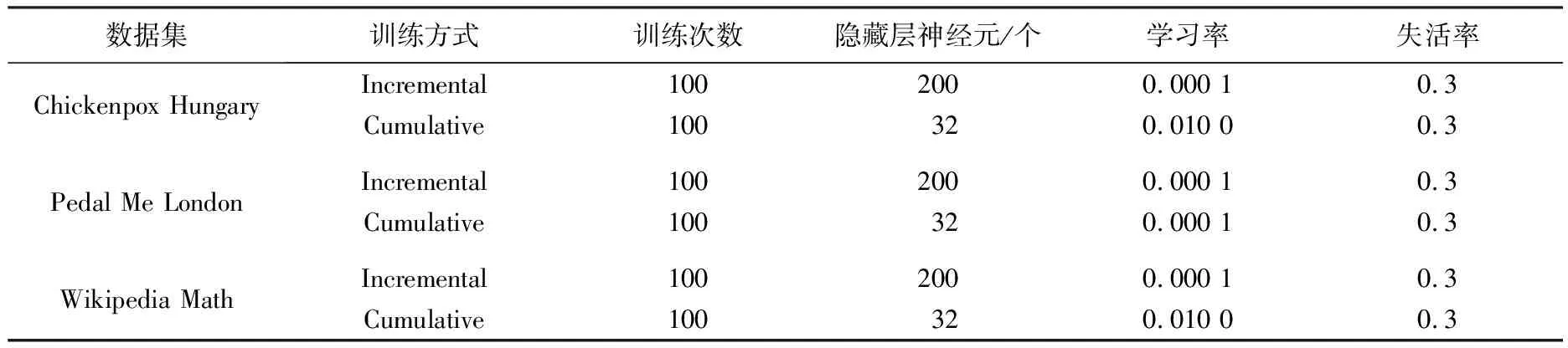
表1 模型超参数

3.3 评估指标

第1个评估指标是均方误差(MSE),是指样本估计值与样本真实值之差平方的期望值.

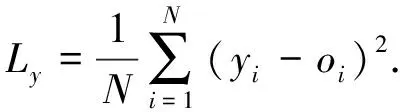
(9)

式(9)中：Ly为样本均方误差;yi表示真实的样本值;o={o1,o2,…,oN}表示模型输出值.

第2个指标是标准差,是用来度量一组数据平均值分散程度的指标,可以反映数据的准确程度.一个较大的标准差,代表大部分数值和其平均值之间差异较大,反之,代表这些数值接近平均值.

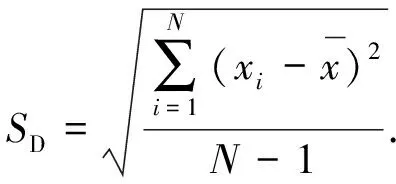
(10)

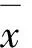
3.4 实验结果与讨论

本文实验的对比数据和对比模型均引自文献[22],以监督学习的方式,把动态图数据集按时序输入模型中,然后输出下一时刻的预测结果.每一个数据集在2种不同的训练方式下重复10次实验,纵向比较其他模型的预测结果,引入均方误差来评价模型的性能并计算标准差用于辅助验证,实验结果见表2.

从表2数据可见,本文提出的GFTLSTM模型在谱域使用Shrinkage作为激活函数后,无论是以Incremental还是Cumulative方式进行训练,在处理离散动态图数据时优于大多数对比模型,这表明本文模型确实可以较好地捕获动态图的内部演化和关联特征,为动态图表示学习提供进一步参考.然而,在Wikipedia Math数据集中,以Incremental为训练方式的实验结果虽然优于绝大多数模型,但并未达到SOTA效果,相比之下,以Cumulative方式进行训练时,实验结果远超其他纵向对比模型.造成这个现象主要有2个原因.首先,Incremental方法是一种基于增量学习的方式,按照时间顺序逐渐添加新的动态图快照进行训练,能够及时捕获图数据的演变特征,适用于实时数据的变化,侧重捕捉数据的动态特性;而Cumulative方法是一种累积式学习方法,将所有动态图快照同时输入模型进行训练,能够综合考虑整个动态图的演变历史,捕捉更全面的动态图特征,侧重捕捉数据的关联关系.由于本文模型在谱域进行低通和高通滤波后,会在空域进行再次整合,并使用长短期记忆网络来捕捉数据中的长程依赖关系,与Cumulative训练方式更契合,这同时也解释了为什么在Chickenpox Hungary和Pedal Me London数据集中,以Cumulative训练方式得到的实验结果优于Incremental训练结果的原因.其次,Wikpedia Math数据集规模庞大,包含大量的节点和边连接关系,因此,在Incremental学习过程中需要处理更大规模的动态数据,每个时序快照中的损失和参数都需要更新,这增加了计算复杂性,加大了模型训练时间和拟合难度,对模型提出了更高的要求.

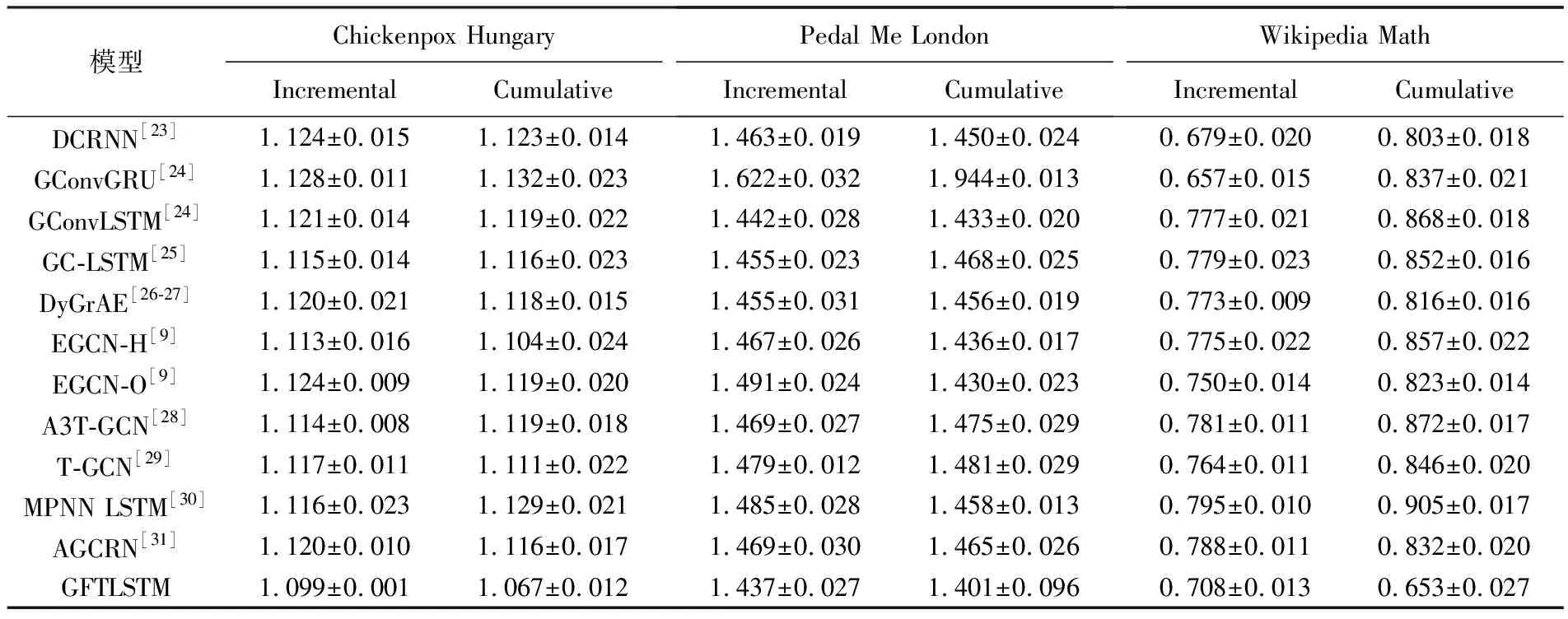
表2 算法比较(均方误差±标准差)

3.5 消融实验及激活函数对比研究

为了验证本文模型在谱域空间中引入Shrinkage函数取代空域激活函数ReLU的有效性,进行消融实验.在实验中,本文将去除函数Shrinkage后的模型标记为GFTLSTM-S.同时,为了进一步验证模型在谱域空间使用多频分析的有效性,在空域中引入了ReLU激活函数,并去除了谱域Shrinkage函数,将该类模型标记为GFTLSTMR.重复进行10次试验,具体的实验结果见表3.

表3 消融实验及激活函数对比实验(均方误差±标准差)

根据表3的结果,在谱域空间去除Shrinkage函数后,通过与表2中的GFTLSTM模型相比,实验结果的均方误差和标准差均有不同程度的提升,这表明模型的性能下降了,验证了引入Shrinkage函数对模型的作用.此外,GFTLSTMR在均方误差或标准差指标上数值都有一定程度的提升,说明实验结果再次变差.因此,在处理离散动态图数据集时,在谱域空间中使用Shrinkage函数来代替ReLU作为激活函数得到的效果更好,这验证了用Shrinkage函数在多频分析中进行信号压缩的价值.

3.6 超参数敏感性实验分析

通过超参数敏感性实验分析可以系统地评估不同超参数对模型性能的影响,从而找到最优的超参数组合.本文模型中的超参数δ用来控制信号压缩的程度,原始信号中大于该阈值的数值才会被输入模型中进行训练;另一个超参数r表示谱域空间中高通滤波器的数量,它与信号刻画程度j共同作用,不同的选择会改变输入特征的维度.

在超参数δ敏感性分析实验过程中,取r=2,设置不同阈值δ后得到的均方误差如表4所示.

表4 超参数δ敏感性分析实验

在超参数r敏感性分析实验过程中,取δ=1e-4,设置不同高阶滤波器数量r后得到的均方误差如表5所示.

表5 超参数r敏感性分析实验

如表4和表5所示,加粗的数值表示不同超参数取值中得到的最优结果.可见在上述2个超参数敏感性实验中,在给定的实验条件下,结果呈现一定的波动,没有明确的最优解,这可能是受到数据集大小、模型的复杂性以及超参数之间的相互影响等因素导致的.在实际应用中,根据具体任务和需求进行超参数的调整更为重要,而不是过于追求单一的最佳设置.

4 结 语

本文提出了一个动态图表示学习的通用框架,初次尝试将小波分析理论、多频分析与动态图表示学习相结合,并在多个动态图数据集上验证了模型的有效性.在未来的工作中,将尝试把模型用于图结构演变的动态图、特征及结构同时演变的动态图及连续动态图中,并结合具体的应用场景,进一步验证模型在不同动态图表示学习任务中的通用性.