城市洪涝风险的多方法组合评估与应用*

王德运，冀承泽，张露丹，吴 祈，郭海湘

(1.中国地质大学(武汉)经济管理学院，湖北 武汉 430074；2.中国地质大学(武汉)自然灾害风险防控与应急管理实验室，湖北 武汉 430074)

近年来，受全球气候变化与城市化进程加速的双重影响，我国城市洪涝灾害事件数呈明显上升趋势[1-3]。据《中国水旱灾害公报》统计资料显示，2006-2018年间，我国平均每年因洪涝灾害导致的受淹城市达164座。由于城市中人口和资产相对集中，导致同等淹没情况下，其损失必然大幅增加[4]。湖北省地处长江中游，辖区年均降水量大，洪涝灾害普发、频发，人员伤亡和经济损失严重[3-4]。仅2021 年8 月8-15 日间，湖北省各市州因强降雨引发的洪涝灾害就造成了158 万人受灾，28 人因灾死亡和31.2 亿元的直接经济损失。长期的理论研究和实践经验均表明，及时、准确的风险评估与预警是有效降低城市洪涝灾害损失的重要途径。

在城市洪涝灾害风险评估领域，目前国内外较为常用的评估方法主要有历史灾情评估法、情景模拟评估法、遥感影像评估法和指标体系评估法[5-7]。历史灾情评估法通过分析历史洪涝灾情数据的数理统计规律，对洪涝灾害风险进行评估和预测。如LANG等[8]结合多学科方法对法国、西班牙两国5个区域展开研究，提出了基于古洪水技术和历史洪水数据的极端洪水风险评估方法。王静静等[9]利用东南沿海四省市50年间的暴雨洪涝资料，绘制了东南沿海地区的暴雨洪涝灾害风险评价图。邱粲等[10]以山东省为研究对象，依据1984-2019年的暴雨洪涝历史灾情及降水量数据，分析了山东省暴雨洪灾的时空变化特征。这种评估方法主要用于早期风险研究，采用的地理数据的质量和精度较低，但需要长时间序列的水文观测数据，评估结论无法显示风险的空间差异[11]。该方法适用于洪涝灾害数据较为全面，时间跨度较大的洪涝风险研究。情景模拟法通过建立不同的情景来模拟洪涝灾害在不同条件下可能产生的影响，以动态评估洪涝灾害的风险程度。WU等[12]基于情景分析，构建一个二维水动力淹没模型，以东莞市为例模拟城市不同情形下的动态淹没。殷杰等[13]结合GIS技术与实地调查，对上海市社区暴雨内涝灾害进行情景分析并评估该研究区的暴雨内涝风险。黄国如等[14]以广州市东濠涌流域为例，通过构建二维耦合的城市洪涝仿真模型，模拟暴雨不同重现期情景下的洪涝过程并评估了洪涝灾害风险。该方法能够基于不同的假设设定不同的情景，从而兼顾了不确定性因素对洪涝灾害风险评估的影响；但其对基础数据要求高，不适用于大空间尺度区域。遥感影像评估法通过卫星遥感监测技术获取淹没区域的灾情信息，结合地理信息系统(GIS)的空间分析技术与地理数据，对洪涝灾害风险进行定量化分析和评估。ISLAM等[15]率先利用孟加拉国洪涝灾害遥感图像数据信息，基于GIS分析数据演示了洪水灾害风险图，并提出了结合洪灾影响频率评估洪灾风险的方法。BURKE 等[16]利用 2000-2015年非洲Chobe流域的红外热成像图像数据，构建多元回归模型，从而识别出洪灾的驱动因素和洪水范围。该方法能直观、实时反映大范围研究区内洪涝灾害的空间分布特征，但其需要大量数据支撑，且有些数据获取难度较大，影像精度也受地形、云覆盖等因素影响。指标体系评估法首先选择影响洪涝灾害风险的因素，建立风险评估指标体系，通过计算权重优化评估体系，最终确定风险指数。DUTT等[17]基于洪水的深度、速度和持续时间等指标，研究构建一个基于概率分布的数学模型用于洪涝灾害损失评估。程朋根等[18]采用随机森林对比分析洪涝指标的重要性，利用层次分析法和熵权法计算指标权重，构建城市洪涝灾害风险评估模型，并以南昌市为例开展实证分析。该方法数据易于获取，能够直观描述洪涝灾害评估指标与洪涝灾害间的相关程度，适用于宏观大区域的洪涝风险评估，但需人为选取指标并且合理设置权重。

在上述多指标综合评价的研究中，由于不同的风险评估方法采用了不同的权重计算模型，因此，所得到的结论往往存在差异，甚至相悖，即“多方法评价结论的非一致性问题”，给决策者进行风险区划带来了较大困难。在已有的研究中，基于单一评估模型的文献在赋权时主要运用专家调查法、层次分析法、二项系数法等主观赋权法，以及主成分分析法、熵权法、CRITIC法等客观赋权法[19]，但不同的单一评估方法往往得出不同的结论。现有研究对于不同评估模型的组合方式也进行了诸多探索，但大多采用的是线性叠加法。但线性叠加法仍然过于主观，未考虑到指标的特异性，很难客观反映指标实际意义，如假设组合权重中不同权重确定方法占有均等的比例[19-21]。

基于一种方法计算的权重可能侧重于反映因变量与某一个或某几个自变量间的相关关系，而无法全面地反映因变量与全部自变量间的相关关系及重要程度，因此，如何通过融合不同方法得到的权重进而得到一套复合权重对于准确评估洪涝灾害风险至关重要。综上，本文以湖北省下辖8个城市为研究区域，首先，建立一套包括城市危险性、暴露性、脆弱性和恢复性的风险指标评估体系，然后，分别采用熵权法和层次分析法计算指标体系的权重并根据Kendall一致性检验结果计算组合权重，最后，基于熵权法、层次分析法、改进组合评价法和加权改进距离系数对不同城市洪涝灾害风险进行定量评估，并结合历史灾情对上述三种评估方法的结果进行对比。对比结果验证了基于复合权重的评估方法相比其他两种方法具有更高的准确性。

1 研究区域与历史灾情概况

湖北省地处中国中部，地理位置位于29°01′53″～33°6′47″N、108°21′42″～116°07′50″E之间，地形地貌呈向南敞开的不完整盆地，中间低平，三面环山，地势以山地、丘陵为主，平原和湖泊面积占少数。该省水系发达(图1)，拥有长江、汉江干流和4 230条河流，总河长6.1万km，其中1 232条河流流域面积50 km2以上，长约4万km。湖北省地处亚热带季风气候区，光照充足，温暖湿润，雨热同季。年平均降水量在800～1 600 mm之间，降水地域分布呈由南向北递减趋势。降水量分布有明显的季节变化，夏季雨量在300～700 mm之间，冬季雨量在30～190 mm之间。2021年湖北省国民经济和社会发展统计公报显示，全省生产总值为50 012.94亿元，人均地区生产总值达到86 416元，完成财政总收入5 745.22亿元，年末全省常住人口5 830万人，城镇化率达到64.09%。鉴于数据可得性原因，本文选取湖北省的武汉市、十堰市、宜昌市、咸宁市、黄冈市、随州市、荆州市及荆门市8个城市作为研究对象，囊括了湖北省东西南北中部，研究区域具有代表性。各城市历史灾情概况见表1。

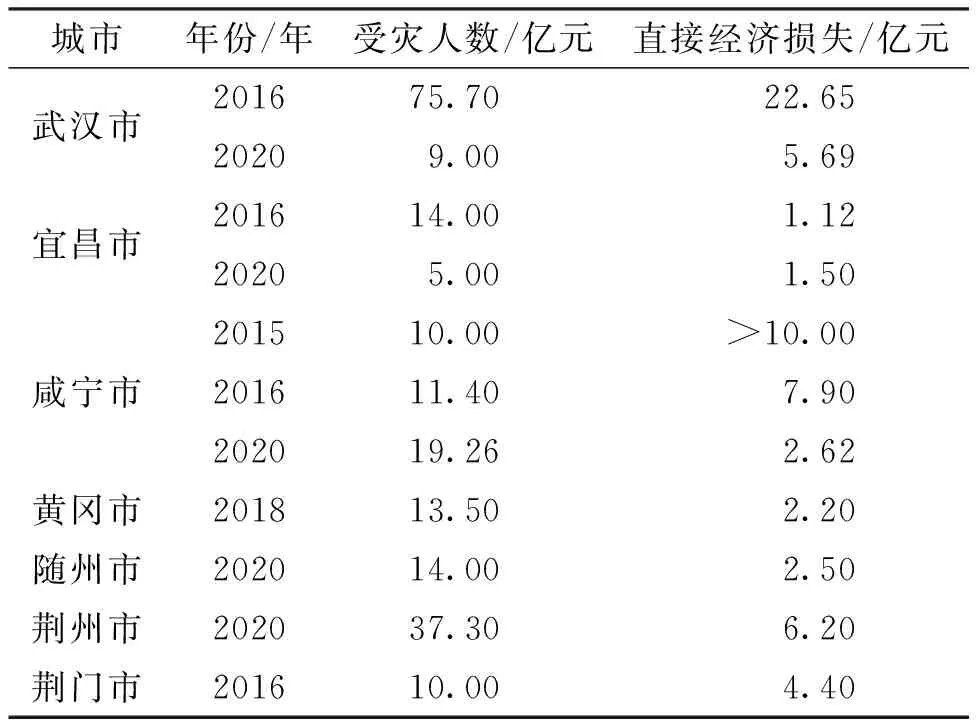
表1 历史灾情概况

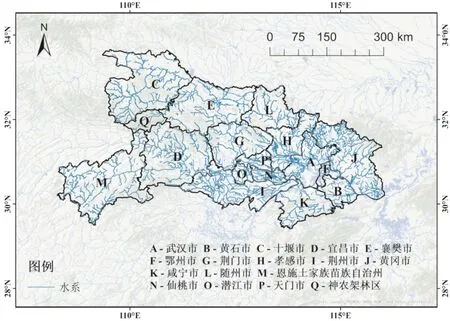
图1 湖北省水系图(审图号：鄂S(2023)009号)

2 研究方法与数据来源

2.1 指标权重的计算方法

2.1.1 熵权法

熵权法根据信息熵的概念来度量指标变异的大小，以此确定指标的权重。一般而言，指标的信息熵越小，即指标提供的信息量越大，其变异程度越大，所占的权重也就越大[22]。基于熵权法计算指标权重的具体步骤如下。

步骤一：数据标准化。X1，X2，…，Xm为n个评估对象及m个评估指标，其中，Xi={x1，x2，…，xn}。记各指标数据标准化后的值为Y1，Y2，…，Ym，则

(1)

步骤二：求各指标的信息熵。

(2)

式中：

(3)

步骤三：确定各指标权重。

(4)

熵权法避免了主观赋权法可能带来的人为偏差，计算结果更为客观和准确。但缺点在于忽略了指标本身的重要程度。

2.1.2 层次分析法

层次分析法通过构建一组层次结构模型，将决策因素划分为不同的层次和因素，然后，通过专家意见打分或以往经验，来判断或衡量同一层次的相对重要性，得到各个指标的权重，进而量化分析比较[23]。层次分析法是一种系统性、简洁实用的定权方法，但是容易受到人为主观性的影响。

基于层次分析法计算指标权重的具体步骤如下：①建立层次结构模型；②构造判断矩阵，采用数字1～9及其倒数作为标度来构造判别矩阵，以衡量各元素之间的重要性程度；③计算指标相对权重；④一致性检验。

2.2 组合权重计算方法

熵权法的计算过程具有严格的数学意义，但忽略了指标本身的重要程度和指标间的相互影响；层次分析法能进行数量化、层次化分析，但很难排除个人主观因素对指标权重的影响。由此，通过将两种方法有机结合，对权重进行修正，可以使其更真实地反映实际情况。基于如上考虑，本文提出了组合权重计算方法，其过程如下。

步骤一：采用Kendall检验对熵权法和层次分析法的赋权结果进行一致性检验[24]。

1)建立假设：H0：n种加权方法结果不一致；H1：n种加权方法结果一致。自由度α=0.01。

2)计算Kendall协调系数

(5)

则Kendall协调系数W为：

(6)

式中：N为指标数，K为赋权方法的个数。

步骤二：根据一致性评估结果计算组合权重。

(1)若Kendall检验结果为一致，则根据以下公式计算组合权重，式中ωj表示第j种方法的指标权重：

(7)

2)若Kendall检验结果为不一致，则采用如下权重组合方法[25]。

①设指标体系共有n个一级指标和m个二级指标，一级指标对应的二级指标个数分别为m1，m2，…，mn，且m1+m2+…+mn=m。利用熵权法确定的权重记为A=(α1，α2，…，αm)。利用层次分析法确定的一级指标权重记为φ=(φ1，φ2，…，φm)，二级指标权重记为B=(β1，β2，…，βm)。

②按照下式将熵权法确定的客观权重αi与层次分析法求得的主观权重βi组合，得到组合权重如下：

Α=(ω1，ω2，…，ωm)。

(8)

式中：

(9)

③将综合权重ωi与对应的一级指标权重φ相乘得到权重如下：

(10)

(11)

④将所得权重A′进行归一化处理，得到：

(12)

其中：

(13)

2.3 基于距离的城市聚类及风险等级划分方法

为准确地划分不同城市的洪涝灾害风险等级，本文结合各城市实际情况将洪涝灾害各指标的风险等级划分为四个等级，即高风险(I)、较高风险(Ⅱ)、中风险(Ⅲ)和低风险(Ⅳ)。标准化后，各指标的不同风险等级矩阵如下所示，其中m为指标数。

(14)

将不同城市的各指标数据按照公式(1)标准化后得到如下矩阵，式中Yim表示第i个城市的第m个指标。

(15)

由此，即可基于下式计算得出不同城市间的距离系数Dij为：

(16)

由于Q型聚类通常认为不同因素对因变量的影响相同，但在实际情况中不同因素对洪涝灾害的影响程度存在较大不同，因此，在计算权重时还要将各因素的比重考虑在内。假设ωi(i=1，2，…，m)表示不同指标的权重，则修正后的距离系数Dij如下：

(17)

根据研究对象的指标值，样本类别由距离系数Dij确定，Dij越小，表明i样本与j样本越相似。因此Dij值最小的列可用来表示研究对象所属的类别。

2.4 数据来源

各指标的数据来源见表2：

表2 数据来源

3 城市洪涝灾害风险评估指标体系构建

参考已有研究[26-27]，本文选取危险性、暴露性、脆弱性及恢复性四个一级指标，并下设13个二级指标，构建城市洪涝灾害风险评估指标体系表(表3)，该指标体系可更为系统全面地评估城市洪涝灾害风险。二级指标的具体数据如图2所示。

表3 城市洪涝灾害风险评估指标体系

图2 湖北省下辖8个城市洪涝灾害风险影响因素

4 基于复合权重的湖北省各城市洪涝风险评估

4.1 基于熵权法的洪涝风险评估

首先，根据式(2)～(4)计算得到各指标的信息熵Ej及权重系数ωj，由此获得熵权法下的二级指标权重：w=(0.043 7，0.043 3，0.032 3，0.034 7，0.125 2，0.139 7，0.047 1，0.074 7，0.052 3，0.088 1， 0.058 3，0.209 3，0.051 3)。然后，根据城市洪涝灾害区划和评估标准，基于加权聚类分析，将城市洪涝灾害风险划分为4个等级。标准化后获得的二级指标的风险等级矩阵如表4所示。

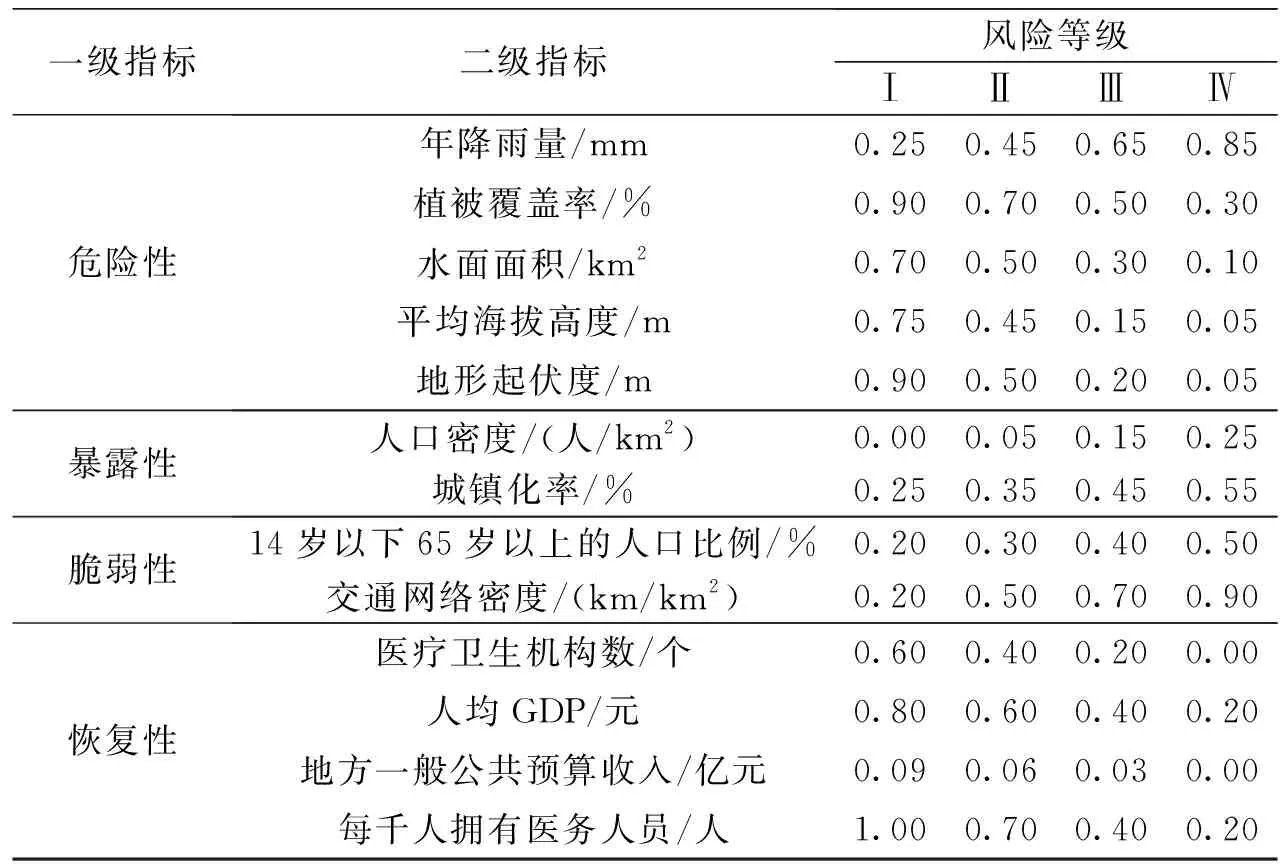
表4 标准化风险等级

计算8个城市标准化后的二级指标数值与熵权法下风险等级系数矩阵的加权聚类系数，得到熵权法的距离系数矩阵如下：

(18)

根据上述距离系数矩阵，以熵权法为例，武汉市所有加权距离系数中最小值的距离系数为0.248 7，据此可将该城市的洪涝风险划入第四类，即该区域的洪涝风险为Ⅳ级。表5显示了各城市风险等级。

表5 熵权法风险等级

4.2 基于层次分析法的洪涝灾害风险评估

4.2.1 指标权重计算

根据以往文献与经验[29-30]，本文确定一级指标重要性排序为：危险性>脆弱性>暴露性>恢复性。进一步根据专家经验法确定一级指标的判别矩阵见表6。

表6 一级指标判别矩阵

由此，计算得出各二级指标权重见表7。

表7 层次分析法得到的指标权重

4.2.2 风险评估结果

同理于熵权法，利用8个城市标准化后的二级指标数值与层次分析法中风险等级系数矩阵的加权聚类系数，得到层次分析法的距离系数矩阵如下：

(19)

根据距离系数得到层次分析法下各城市风险等级如表8所示。

表8 层次分析法风险等级

4.3 基于组合权重的洪涝灾害风险评估

4.3.1 指标权重的一致性检验及组合权重计算

首先，基于Kendall法判断两套权重的一致性程度，过程如下。

步骤一，建立Kendall检验假设：H0为两种加权方法结果不一致；H1为两种加权方法一致。自由度α=0.01。

步骤二，计算Kendall协调系数。

Kendall协调系数的数值很小，接近于0，不能拒绝原假设，因此，由上述结果可得，这两种指标赋权方法所得到的权重结果不一致。由此，需按照第二种方式计算组合权重，计算过程如下。首先，基于式(8)将熵权法与层次分析法所得权重进行组合，得到组合权重：A=(0.179 4，0.012 2，0.066 1，0.031 9，0.082 5，0.349 1，0.039 3，0.031 5，0.110 1，0.058 1，0.007 5，0.017 0，0.015 4)。然后，将组合权重与层次分析法求得的一级指标权重相乘并进行标准化处理，得到最终权重为w= (0.302 7，0.020 6，0.111 5，0.053 9，0.139 2，0.245 0，0.027 6，0.016 7，0.058 6，0.014 3，0.001 8，0.004 2，0.003 8)。

4.3.2 风险评估结果

同理于熵权法，利用8个城市标准化后的二级指标数值与组合权重中风险等级系数矩阵的加权聚类系数，得到组合权重下的距离系数矩阵如下：

(20)

根据距离系数得到组合权重下各城市风险等级如表9所示。

表9 组合权重风险等级

4.4 三种评估方法的比较

对比三种方法的洪涝灾害风险图(图3)，结合各城市历年洪涝灾害历史数据，可以发现基于组合权重的风险等级划分更符合实际情况，较其余两种方法更优。

图3 洪涝灾害风险等级对比

由基于复合权重的湖北省洪涝风险评估结果可知(表9和图3)，咸宁市的洪水灾害风险在8个城市中最为显著，当地洪水灾害属于I级高风险；武汉市、宜昌市、黄冈市属于Ⅱ级较高风险。统计数据表明，位于湖北省东南部的武汉市、咸宁市和黄冈市由于降雨量大、地形起伏较为平缓，在暴雨环境中容易形成汇流区。此外，武汉市人口众多，因此，一旦发生洪涝灾害，社会经济将受到更大影响；而咸宁市和黄冈市经济水平与医疗水平较其他城市相对偏低，洪水灾害的脆弱性无法通过其良好的可恢复性来弥补。位于西南部的宜昌市地形复杂，地形标准差大，容易引起山洪、泥石流等灾害。

洪水灾害风险中等的荆州市和荆门市总体风险不大，但仍存在局部风险。例如，荆州市的植被覆盖率过低，排水能力弱，地形起伏度较小。因此，一旦形成积水，该城市将很难及时排水。但荆州市恢复性良好，可弥补部分洪涝灾害的危险性。荆门市降水量相对其他城市而言较少，危险性较低，但医疗水平不高，恢复性差。

洪水灾害风险较小的十堰市和随州市为低风险区域。统计数据显示，十堰市位于湖北省西北部，降雨量少，植被覆盖率高，地形起伏度大，难以形成大面积积水。此外该城市恢复性不存在明显短板，因而，洪涝灾害风险等级较低。随州市位于湖北省北部，降雨量较少，人口密度低，经济发展较为缓慢，总体来说洪涝灾害风险较低。

综上所述，湖北省下辖的上述八个城市中有一个高风险地区，三个较高风险地区、两个中风险地区和两个低风险地区。评估结果与城市实际情况较为一致，表明组合评估方法具有更高的准确性。

5 总结与讨论

本文通过梳理国内外城市洪涝灾害风险评估的相关研究，从城市暴雨的危险性、暴露性、脆弱性和恢复性出发，建立了湖北省下辖8个城市的洪涝灾害风险评估指标体系。针对指标体系评估法中存在的“多方法评估结果非一致性问题”，分别采用熵权法、层次分析法和改进组合评价法计算指标权重，利用加权改进距离系数进行聚类分析，进而确定不同城市的洪涝灾害风险等级，并结合历史灾情对三种评估方法的结果进行对比，对比结果验证了基于复合权重的评估方法相比其他两种方法具有更高的准确性。

从综合评估结果来看，咸宁市的洪涝风险处于高风险状态，其风险水平主要受到降雨量大和经济医疗水平落后的影响。武汉市、黄冈市和宜昌市的洪涝风险处于较高风险状态，洪涝驱动因子主要包括降雨量大、人口较多、地形标准差大，在暴雨环境中容易形成汇流区。荆州市和荆门市的洪涝风险处于中风险状态，总体风险不高。其中，荆州市虽危险性高，但恢复性良好；而荆门市降雨量较少，危险性较低。十堰市和随州市的洪涝风险处于低风险状态，两市洪涝危险性低，恢复性不存在明显短板，不容易发生洪涝灾害。