二沉池一维模型的不确定性分析

李 犇，郑 宇

（中国中化控股有限责任公司质量健康安全环保部，北京 100031）

二沉池被普遍用于泥水分离，使混合液澄清、污泥浓缩并将分离的污泥回流到生物处理段。由活性污泥模型与二沉池模型耦合形成的污水处理模型被广泛用于污水处理过程的学术研究和运行策略制定[1]。Takacs 模型[2]已被许多商业模拟软件作为二沉池模拟参考模型[3]，但也存在二沉池中多种沉淀形式的描述不充分、模型的数值求解不够精确等问题[4]。为克服Takacs 模型局限性，研究人员通过使用更精确的数值算法、考虑压缩沉淀和水力弥散对二沉池的影响等方法开发一系列新二沉池一维模型[4-6]。但是，缺乏成熟的模型使用指南等问题仍阻碍着新开发的二沉池一维模型在实践中的应用。本研究利用废水处理基准模型BSM1[7]作为运行平台，对4 种二沉池一维模型在不同运行条件下的不确定性进行分析，为不同预测目标下选择合适的二沉池模型提供参考。首先，本研究通过不确定性分析评估不同二沉池模型在二沉池极端运行条件下预测结果的差异。其次，本研究通过不确定性分析评估二沉池模型的选择是如何影响极端条件下二沉池的运行决策。

1 数据和方法

1.1 一维模型方程和模拟过程条件

本研究利用废水处理基准模型BSM1 作为运行平台，活性污泥模型AMS1 与二沉池一维模型耦合对活性污泥系统代谢和沉淀过程进行完整模拟。关于活性污泥模型ASM1 的更详细信息，可参考相关文献[7]。4 种具有代表性的二沉池一维模型因其在数值解法、沉淀过程描述等方面的差异被用于比较研究，分别是Takacs 模型、YRD 模型[4]、区域-压缩沉淀模型[5]和Burger-Diehl 模型[6]。基于区域沉淀主导二沉池中污泥沉淀过程的假设，根据质量守恒定律，Takacs 模型方程如式（1）所示。其中，F是固体通量，其表达式如式（2）所示；vhs是区域沉淀速度[8]，由式（3）计算得到。

式中：C是污泥浓度，kg/m3；t是时间，h；x是距离二沉池池底高度，m；Qf是进水流量，m3/h；A是二沉池表面积，m2；Cf是进水污泥浓度，kg/m3；δ为狄拉克控制函数，数值取1 或0；Qe是出水流量，m3/h；Qu是底流流量，m3/h；Ce是出水污泥浓度，kg/m3；Cu是底流污泥浓度，kg/m3；v0和rh是区域沉淀参数。

YRD 模型和Takacs 模型有相同的模型方程，但YRD 模型采用Yee-Roe-Davis 数值通量作为数值解法，求得的数值解具有二阶精度。根据质量和动量守恒定律，区域-压缩沉淀模型方程如式（4）所示。其中，dcomp(C)是压缩沉淀方程[5]，如式（5）所示。

式中：g是重力加速度，m/s2；ρs是污泥密度，kg/m3；ρf是废水密度，kg/m3；Cg是压缩沉淀临界浓度，kg/m3；α是有效固体应力参数，Pa；β是有效固体应力参数，kg/m3。

相较于区域-压缩沉淀模型，Burger-Diehl 模型进一步考虑水力弥散作用对二沉池运行的影响，其方程如式（6）所示。其中，ddisp(vov)是水力弥散方程，如式（7）所示。

式中：vov是溢流率，m/d；dC,0是最小水力弥散系数，m2/d；vov,C是水力弥散方程控制溢流率，m/d；γ是控制关于vov,C一元二次方程的系数，d。

为了全面评估4 种二沉池模型，本研究运用BSM1 平台模拟2 种二沉池极端运行条件。极端运行条件1 为雨天且污泥具有良好沉降性。首先根据ALEX 等[7]提供的非雨天天气数据，进行为期100 d 的模拟使模型预测值达到稳定状态，然后通过将流入流量增加到非雨天天气流入流量的4 倍来模拟雨天情况（时长4.8 h）。污泥正常状态和膨胀状态下，4 种一维模型参数的取值范围如表1所示。极端运行条件2为雨天且污泥膨胀导致沉降性变差。首先进行为期100 d 的模拟，使模型预测值达到稳定状态，然后通过将流入流量增加到非雨天天气流入流量的2 倍来模拟雨天，并将一维模型参数调整到表1 污泥膨胀范围内来模拟污泥膨胀（时长3.6 h）。

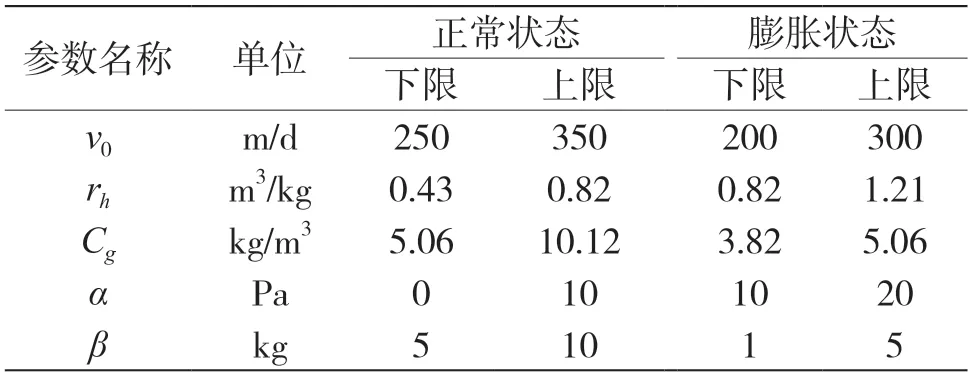
表1 污泥正常状态和膨胀状态下二沉池模型参数取值范围

1.2 基于蒙特卡洛方法的不确定性分析

不确定性分析对于提高模型在实践应用中的可靠性具有重要意义。蒙特卡洛方法以概率统计理论为基础，可用于分析各种不确定性问题。本研究采用蒙特卡洛方法对4 种沉淀池模型进行不确定性分析，且蒙特卡洛随机采样法重采样次数为2 000 次。

2 结果与讨论

极端条件1 下，4 种二沉池模型关于污泥层高度、底流污泥浓度预测值的箱线图如图1所示。其中，模型1 表示Takacs 模型，模型2 表示YRD 模型；模型3 表示区域-压缩沉淀模型；模型4 表示Burger-Diehl 模型。4 种模型中，YRD 模型预测的污泥层高度最低，例如，YRD 模型预测的污泥层高度平均值为1.4 m，小于Burger-Diehl 模型预测的2 m。尽管Takacs 模型和YRD 模型都仅考虑区域沉淀对二沉池运行的影响，但Takacs 模型数值求解存在较大的数值弥散，相对于YRD 模型，污泥层高度预测值更大。区域-压缩沉淀模型和Burger-Diehl 模型都考虑压缩沉淀，压缩沉淀会阻碍污泥向二沉池底部输送，所以区域-压缩沉淀模型和Burger-Diehl 模型预测的污泥层高度较YRD 模型更大。除压缩沉淀外，Burger-Diehl 模型还考虑水力弥散作用，水力弥散有利于污泥向二沉池澄清区输送，因此Burger-Diehl 模型预测的污泥层高度最大。相应地，YRD 模型仅考虑区域沉淀且数值弥散较小，有利于污泥向二沉池底部输送并浓缩，其预测的底流污泥浓度最高。

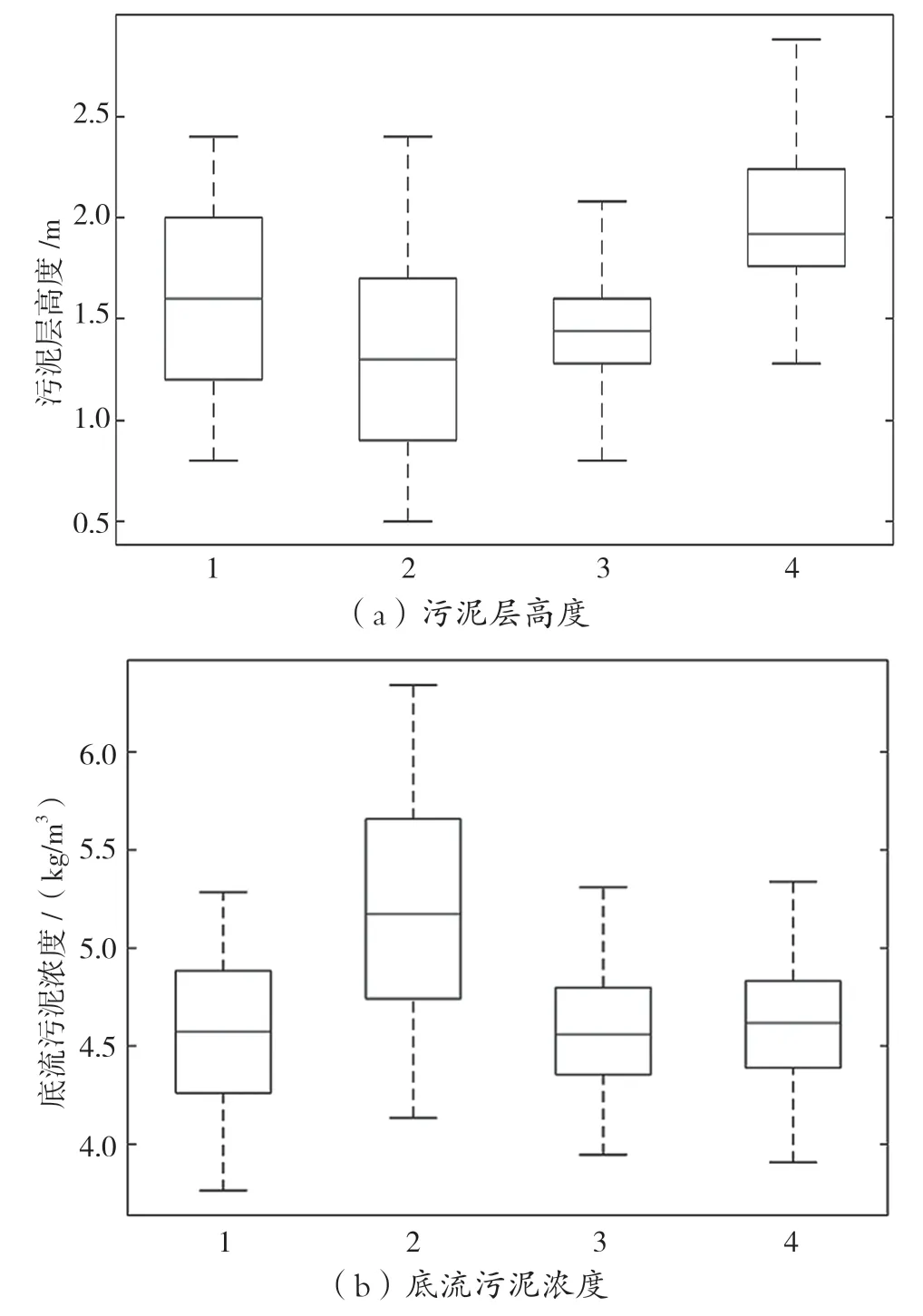
图1 极端条件1 下二沉池模型关于污泥层高度、底流污泥浓度预测值的箱线图

极端条件2 下，4 种二沉池模型关于出水污泥浓度预测值的累积分布如图2所示。如果将出水污泥浓度控制标准设为0.03 kg/m3，Takacs 模型、YRD 模型、区域-压缩沉淀模型和Burger-Diehl 模型预测出水污泥浓度超过控制标准的可能性分别为14.35%、1.45%、0.89%和11.47%。

如果将Takacs 模型或Burger-Diehl 模型预测结果用于制定二沉池运行策略，就需要通过增加底流流量等措施降低出水污泥浓度，避免超过出水标准。然而，如果使用YRD 模型或区域-压缩沉淀模型预测结果作为参考，就没有超标风险，不需要调整系统运行方式。

3 结论

本研究对4 种二沉池一维模型在雨天、污泥膨胀等极端运行条件下的不确定性进行分析。在雨天、污泥膨胀等极端运行情况下，二沉池模型的选择会显著影响二沉池运行情况不确定性预测。YRD 模型会预测最低的污泥层高度和最高的底流污泥浓度。Takacs模型数值求解存在较大的数值弥散，相对于YRD 模型，污泥层高度预测值更大，而区域-压缩沉淀模型和Burger-Diehl 模型中压缩沉降会阻碍污泥向二沉池底部输送和浓缩，从而导致较大污泥层高度和较低底流污泥浓度。在雨天、污泥膨胀等极端运行情况下，二沉池预测结果不确定性分析有助于及时调整二沉池运行方式，避免出水污泥浓度超标等问题发生。4 种模型预测结果不确定性分析表明，二沉池模型的选择会显著影响不确定性分析结果，从而进一步影响二沉池运行策略的调整。