混合润湿性柱状纳米结构对铜板上纳米氩膜沸腾传热的影响

刘峰瑞, 陈占秀, 李源华

(河北工业大学 能源与环境工程学院, 天津 300401)

1 引 言

近年来，随着微电子技术的发展，系统设备的体积和面积越来越小，各种微纳器件的热管理成为亟待解决的核心问题，需要尽可能高效地强化热交换. 在沸腾相变传热过程中，液体需要吸收大量的汽化潜热，增加了传热速率. 因此，高效率、高传热率的沸腾相变热迅速成为各类学者研发的重点[1-3]. 沸腾相变行为和传热效率受到许多因素的影响，例如流体性质、壁性质和外部条件. 其中，壁面润湿性和壁面纳米结构起主导作用.

对于沸腾传热，表面纳米结构的几何形状和尺寸，作为刺激气泡成核生成的构型[4]，对核态沸腾过程有重要影响. 研究人员通过修改加热表面的拓扑结构，例如周期性正弦表面、纳米通道结构表面和锥形纳米结构表面，模拟了纳米结构对爆炸沸腾的影响，发现与平面相比，它们显著增强了从固体表面到液体的热量传递，并促进了相变过程中的传热[5-7]. 此外，Wang和Zhang等人[8，9]通过分子动力学研究发现，纳米结构对成核沸腾的初始成核时间和初始温度有显著影响. 与光滑表面相比，纳米结构表面的临界热通量显著增加，气泡成核增强，初始成核时间缩短. Liu等[10，11]发现粗糙结构使沸腾起始时间提前，蒸发质量通量增大. 并提出随着表面积的增加，界面吸附的水分子越多，单位面积的相互作用能就会增加，从而降低界面的热阻. 在这项工作中，Liu等人[12]研究了内表面粗糙度对凹面纳米结构沸腾传热性能的影响. 结果表明，传热性能强烈地依赖于粗糙元的结构. 低固体含量配置具有更好的传热性能，并可延迟沸腾过程的开始. 傅等人[13]进行了分子动力学模拟，以研究纳米结构对被热铜板突然加热的水的快速沸腾的影响. 研究表明，纳米结构对固体铜片到液态水的能量传递和液态水到蒸汽的相变过程有显著影响. 仍有一些关于纳米结构对固/液界面传热的影响的研究[14-18]，这也表明结构化表面可能是爆发沸腾的主导机制之一. 润湿性对气泡成核有很大影响. 周等[19]研究了液氩在不同润湿性的图形化表面上的气泡成核. 发现疏水部分的面积比影响气泡的成核温度. 提出了一个最佳的面积分数，以尽量降低气泡成核温度. Wu等人[20-21]研究了在不同润湿性条件下光滑和粗糙铜表面上水膜的快速沸腾. 研究发现，与纯润湿表面相比，混合润湿表面通过调节蒸汽在加热铜表面的扩散行为来强化沸腾传热，而纳米通道高度的增加有利于成核点的形成和蒸发. Diaz等人[22]研究了疏水/亲水纳米图案增强沸腾传热的功效. 结果表明，亲水纳米柱和亲水性壁的组合表现出最佳的传热性能. Shahhardi等人[23]研究了表面润湿性对沸腾引发、气泡成核和生长的影响. 观察到亲水表面会加速气泡的成核，但减缓气泡的膨胀速度，从而延缓蒸汽膜的形成. Hens等人[24]发现气泡成核和蒸汽膜的形成取决于固-液界面的润湿性. 亲水表面为气泡成核和蒸汽膜形成提供了有利条件. 此外，也有研究者[25-27]通过设计混合润湿性来研究薄液膜的爆炸沸腾过程. 结果表明，混合湿壁更容易引发沸腾现象，对气泡起始温度、膜态沸腾温度和蒸发速率有显著影响.

上述研究揭示了纳米尺度下池沸腾的部分机理. 在传热过程中，纳米结构和表面润湿性都起到促进作用，但很少有研究将上述两个影响因素结合起来进行分析. 本文采用分子动力学方法在纳米尺度上模拟了液态氩在铜表面的快速沸腾，构建了具有混合润湿性的圆柱纳米结构壁，然后改变纳米结构的高度和疏水部分的比例，观察其对沸腾传热的影响.

2 模拟细节与方法

2.1 物理模型

创建了一个尺寸为91 Å(X)×91 Å(Y)×543 Å(Z)的模拟框，模拟系统的初始配置如图1所示，系统沿x轴和y轴采用周期性边界条件，z轴采用固定边界，模拟体系由固体区域、液体区域和气体区域三部分构成. 此外，假设模拟系统的顶部边界是反射的，当氩原子试图穿过反射墙时，它将被反弹，该过程不会产生能量交换和损失. 模拟工质为铜和氩. 工质选用氩原子是因为氩的性质稳定，势函数简单，可以很大程度上节约计算时间. 模拟过程中求解L-J势能时采用球形截断处理，截断半径选取为10 Å. 氩的晶格常数为5.72 Å. 铜原子呈面心立方 (FCC)晶格结构，晶格常数为3.62 Å. 对于所有壁面，固定层原子保持静止，由2500个铜原子组成，防止壁面受热变形. 紧接着是作为系统中的热源的幻影原子“phantom atoms”[28]，由6250个铜原子组成，其温度通过恒温器来维持. 铜原子受到大小为-Kr的弹簧力的约束，其中K是弹性常数，为0.293 eV/nm[29]，r是原子从当前位置到其初始位置所在位置的距离，以便铜原子在整个模拟过程中交换能量时会围绕其原始位置振动. 将Lennard-Jones(12-6)势能模型应用于氩原子、铜原子之间的相互作用力的计算.

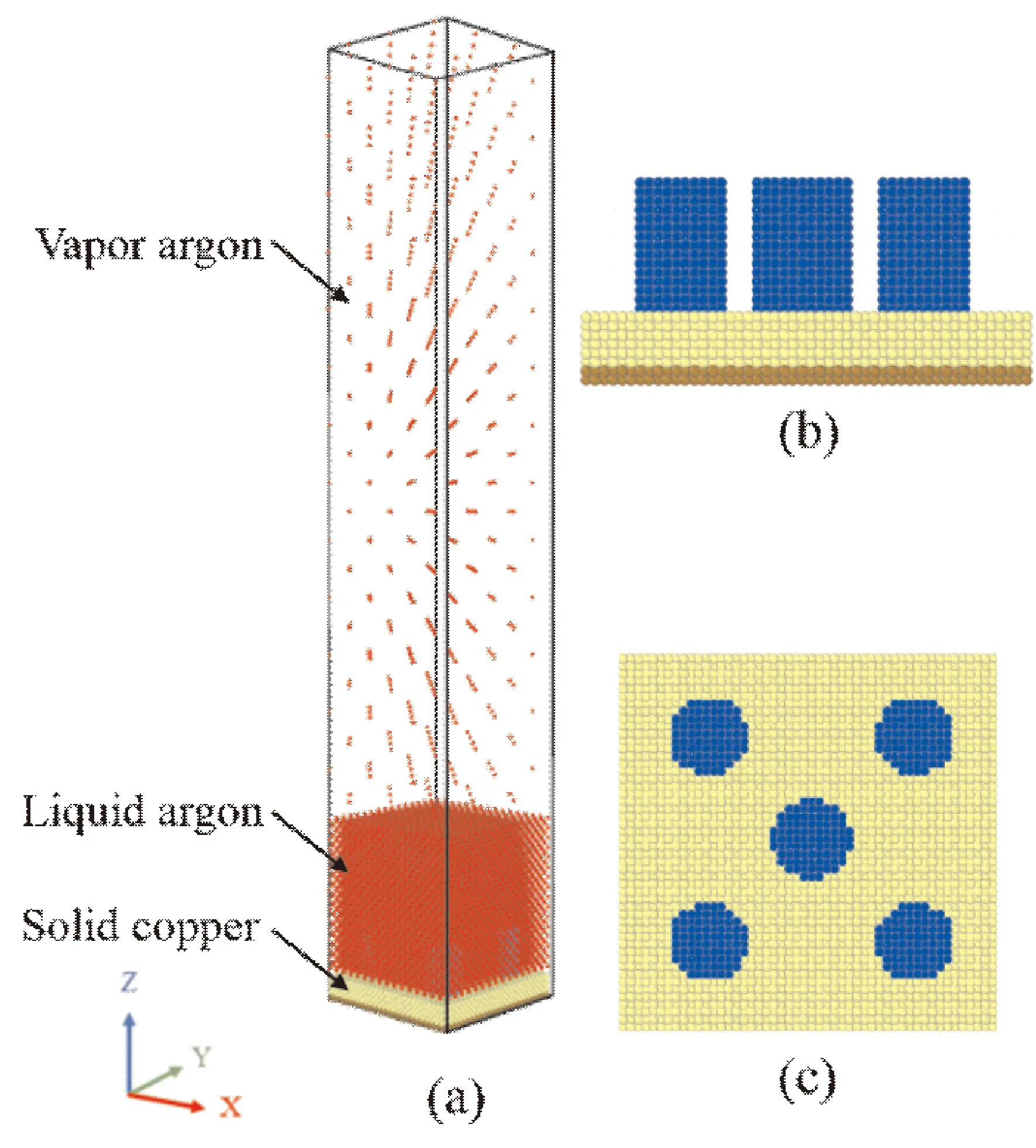
图1 模拟系统初始配置示意图：(a)总体视图；(b)壁面正视图；(c)壁面俯视图Fig. 1 Schematic diagram of the initial configuration of the simulation system：(a)overall view；(b)front view of the wall；(c)top view of the wall

在本文所有模拟中，基底厚度都超过了其截断半径距离，这保证了壁面厚度不会影响模拟结果. L-J(12-6)势能函数表达式：

(1)

其中，rij为计算粒子对之间的间隔距离，在计算氩-氩原子对之间相互作用力时，能量参数ε和尺寸参数σ选择为：ε=0.0104 eV，σ=0.3400 nm. 当计算铜-铜原子对之间相互作用力[30]时，能量参数ε和尺寸参数σ选取为ε=0.2047 eV，σ=1.9297 nm. 为了描述氩原子和铜原子之间的相互作用，采用Lorentz-Berthelot混合法则[31]进行求解，特征长度由下式计算：

(2)

正如之前的研究[32]所提到的，可以通过改变描述壁面和液态氩原子之间相互作用的 LJ 势的能量参数来调整润湿性. 当εAr-Pt=0.5εAr-Ar(0.0052 eV)，获得亲水材料，当εAr-Pt=0.25εAr-Ar(0.0026 eV)，获得疏水材料. 如图2显示了润湿性占比不同的纳米结构壁面，底面黄色和圆柱上深蓝色代表亲水部分，浅蓝色代表疏水部分. 在这项工作中，圆柱纳米结构柱宽为1.6 nm，有两个不同的高度hc，分别为1.5 nm和2.5 nm，其中疏水部分占圆柱比β分别为0、33%、53%和73%.

图2 润湿性占比不同的纳米结构壁面案例：(a)β=0 (b)β=33% (c)β=53% (d)β=73%Fig. 2 Cases of nanostructured walls with different wettability ratios：(a)β=0 (b)β=33% (c)β=53% (d)β=73%

2.2 模拟方法

模拟初始情况下，将包含15200个氩原子的液膜放置在基板上方. 为了减少模拟计算成本，在每次模拟开始时使用共轭梯度 (CG)算法最小化整个系统的能量，时间步长设置为5fs. 随后将NVT(恒定原子数、体积和温度)系综应用于整个系统，使其在90 K下运行1ns达到平衡状态. 达到稳定后，改为微正则(NVE，即恒定原子数、体积和能量)系综. 最后，通过恒温器将热源层铜原子的温度瞬间升至160K，以诱导液膜的爆炸沸腾现象. 所有模拟均使用开源经典MD 代码大规模原子/分子并行模拟器 (LAMMPS)[33]进行，并使用开放可视化工具 (OVITO)[34]进行可视化.

2.3 模型验证

模型验证采用Yin 等人[35]的工作，模拟了液氩在光滑铜表面上的池沸腾过程. 计算时采用文献[35]中的模拟参数. 计算如图3所示，将液氩温度随时间的变化情况和液氩发生沸腾脱离铜表面的时间与文献中的结构进行了比较. 本文计算结果与文献中的结果相比，液氩温度的最大误差为 5.9%，发生沸腾时间的误差为5.0%，两者计算非常相近证明本文计算结果的正确性.

图3 验证结果：(a)液氩温度随时间变化；(b)液氩发生沸腾脱离铜表面的时间.文献[35](左)和当前模拟(右)Fig. 3 Verification results：(a)temperature of liquid argon as a function of time；(b)time for liquid argon to boil off the copper surface. Reference [35](left)and current simulation (right)

3 结果与分析

3.1 固壁上液氩的池沸腾过程

本文给出了两种圆柱高度情况下不同混合润湿性表面液氩池沸腾的过程，快照如图4所示.在这里，β=0表示疏水占比为0，即固体壁面为全亲水. 模拟初期，液膜均与底面相接触，并未因增加疏水占比而浮于圆柱上方. 首先，如图4(a)当hc=1.5 nm，β=0时，在加热初期，系统处于纯蒸发阶段，仅在液-气界面处发生液膜向蒸汽氩原子的转变直至13.50 ns时，底部液体层出现气泡或缝隙，在14.40 ns气泡聚结形成蒸汽膜，将液体与壁面分开并推动其向上运动，发生沸腾；之后壁面与液膜间的氩原子及液膜中的氩原子仍然继续被加热形成气态氩原子. 对比图4(b)圆柱高度为2.5 nm，初始时表面蒸发形成的气态氩原子较多，固液之间形成蒸气膜的时间提前到了8.30 ns. 其余六个增加疏水占比的表面，它们都有着相似的沸腾过程. 然而，就沸腾发生时间而言，发现相同柱高情况下，β越大发生的越快，这表明传热效率更高. 具体来讲，Case7到达沸腾起始时间为10.25 ns，而Case5需要的时间相对较长，为11.75 ns. 另一方面，当柱高增加到2.5 nm，β=33%、β=53%和β=73%时发生沸腾的时间分别比柱高为1.5 nm时提前了4.55 ns、5.1 ns和4.4 ns. 我们注意到，增加疏水占比后气泡并不再只出现于圆柱底部，而是出现在亲疏水交界处或疏水部分顶部. 其原因可以推断为与疏水部分接触的Ar原子受到其影响，在接下来的非平衡分子动力学过程中，这部分Ar原子不断吸收热量并率先突破液体内部分子间作用力，脱离两原子之间的相互束缚而运动，且距离不断增大，使气泡时间提前，促进气泡形核，加速了爆炸沸腾的过程. 总结液氩沸腾的起始温度和时间如图5所示. 从图中可以看出，对于两种柱高，随着疏水占比β的增大，都会降低爆炸沸腾的起始温度和起始时间. 因此我们得出本文提出的亲疏水性混合的圆柱纳米结构壁面对爆炸沸腾起着促进作用.

3.2 液氩沿Z方向的密度分布

相变过程的变化也可以用壁面上部的瞬态空间密度变化来描述. 当气泡核在液膜中产生时，近壁成核区的密度会降低. 为获得密度剖面，将仿真系统沿z方向分为50个高度为10.84 Å的切片，每1 ns输出一次每个切片的密度. 液氩在不同柱高混合润湿性表面上密度剖面的变化趋势如图6所示. 由图可知，柱高为1.5 nm的不同混合润湿性壁表面经历9 ns的蒸发阶段后，近壁面处液氩数密度大概在0.016 ρσ3，柱高为2.5 nm的不同混合润湿性壁表面经历4 ns的蒸发阶段后，近壁区液氩数密度大概在0.018 ρσ3. 随着加热时间的增加，液体中会产生蒸汽，导致密度下降，近壁面处形成低密度区，距离壁面较远处氩密度增加同时，产生的蒸汽将一层厚厚的液膜提升到z方向较高的位置，并且由于系统温度的升高，该液膜的密度峰值也逐渐减小. 我们发现，由于case1沸腾起始时间较晚，长时间的蒸发使其近壁面区氩密度降低到了0.01ρσ3左右，远壁面处氩密度才开始增加；然而case2、case4、case6和case8随着β的增大，发生沸腾的时间不断加快，高密度区出现在系统越来越高的地方. 另一方面，在50 Å左右的位置总是有一个密度读数，这是由于表面附近吸附氩原子而形成的液态氩薄层.

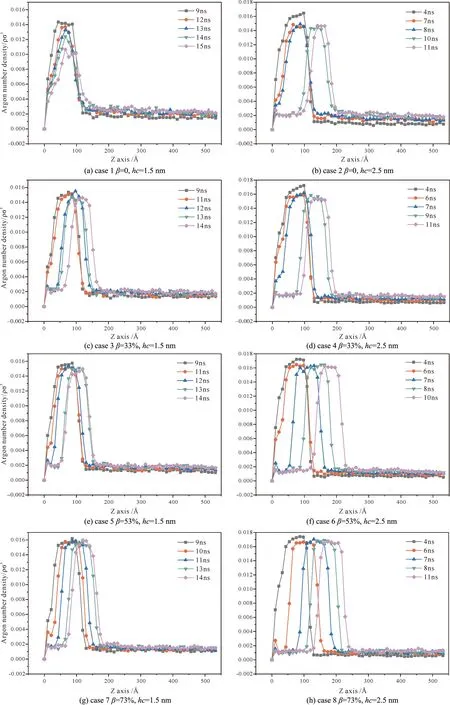
图6 液氩在不同柱高混合润湿性表面上沿z方向的密度分布Fig. 6 Density distribution of liquid argon along the Z-direction on mixed wetted surfaces with different column heights

3.3 液态氩原子蒸发速率

净蒸发原子数的变化能够很好的显示出加热过程中的相变速率. 本文计算净蒸发原子数的方法是通过在给定截止距离0.53 nm内的每个氩原子的相邻原子数，当指定氩原子周围的相邻原子数小于7，则认为它是蒸气原子. 否则，它被认为是液态氩原子. 该方法已在文献[36，37]中广泛使用. 观察图7，随着液膜不断吸收热量，不同柱高混合润湿性表面上液态原子均被蒸发，其数量首先在蒸发阶段快速减少. 当液体蒸发一段时间后发生沸腾，液态原子随时间减少趋势开始变缓，这种趋势随着β的增大出现的越来越早，柱高为1.5 nm时，β=0、β=33%、β=53%和β=73%分别在14.5 ns、12 ns、11.8 ns和10 ns附近减少的速率放缓，这正好大致对应于液氩沸腾的起始时间. 正如我们所预想的，在相同的疏水占比情况下，柱高为1.5 nm的壁面上液体原子数均小于柱高为2.5 nm的，如β=53%时，因为柱高增加后的沸腾温度128 K要低于1.5 nm时的135 K，且在更短时间内发生沸腾. 由于较高的沸腾温度和更长的沸腾起始时间，使得蒸发过程持续时间更久，气态氩原子更多，壁面上液体原子数较少.

图7 不同柱高混合润湿性表面上液体原子数随时间变化Fig. 7 Variation of the number of liquid atoms with time on the mixed wetted surfaces with different column heights

3.4 液氩温度及能量变化

图8(a)给出了不同柱高混合润湿性表面液氩温度随时间变化情况，观察到，两种柱高的传热速率和最终温度呈现出Tβ=0>Tβ=33%>Tβ=53%>Tβ=73%的规律.β=0%时，液氩升温速率最快，但因其为纯亲水结构，对液氩具有很强的吸引力，需要更高的温度才能发生爆炸沸腾现象. 但是当圆柱增加了73%疏水占比后，最先达到沸腾温度点，发生固-液分离现象并使温度变化出现拐点. 温度变化体现了液氩吸收能量的大小，故图8(b)给出了不同柱高混合润湿性表面上液氩的动能与势能变化. 我们知道，体系吸收的动能与势能之和为体系吸收的总能量，总能量显示出与温度几乎一致的变化规律. 如β=53%时，系统总能量增量先迅速增大，随后由于固-液分离，吸收能量减缓，并保持较低的增长率直至模拟时间结束，表明液氩仍在与壁面进行能量交换. 此外，柱高相同时，随着β的增大，能量增量曲线出现拐点的时间提前，即系统达到沸腾所需要的能量随之减少. 仔细观察动能势能变化ΔE*，可以得知吸收的能量主要转换成了势能，使其在某刻冲破势能壁垒，即导致气泡核的形成和生长.

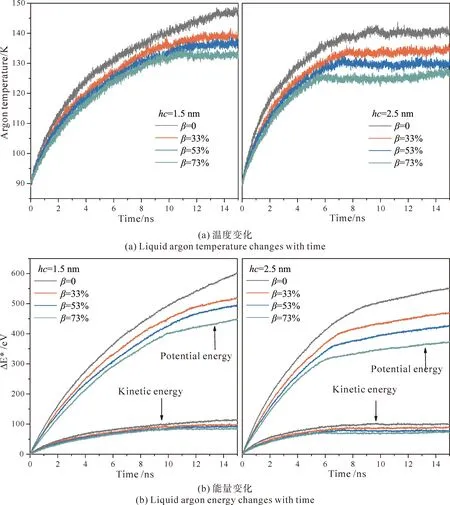
图8 不同柱高混合润湿性表面上液氩温度及能量变化随时间变化情况Fig. 8 Variation of liquid argon temperature and energy with time on the mixed wetted surfaces with different column heights

为了进一步研究β对沸腾传热的影响，本文计算了不同柱高混合润湿性表面上的热通量随时间变化情况，如图11所示. 固体和流体原子之间的热通量由下式计算：

(3)

其中Asub是x-y平面上的截面积. 由于在t=0 ns时表面温度突然从90 K升高到160 K，而液膜的温度仍然平衡状态时的90 K，此时液膜与壁面的温差达到最大. 因此，不同柱高混合润湿性表面上的热通量在初始时刻达到最大值. 随着传热过程的进行，固-液温差不断减小，使得热通量下降. 观察图9，β相同时，柱高为2.5 nm的混合润湿性表面上热通量曲线出现拐点的时间比柱高为1.5 nm时提前，且热通量下降时的斜率更大，传热更剧烈. 我们发现，出现拐点原因是在发生沸腾时底部出现蒸汽膜，使得传热性能恶化，柱高相同时，随着β的增大，拐点提前出现. 这说明亲疏水性混合的圆柱纳米结构壁面可以强化换热速率，从而导致更快的爆炸沸腾.

传热系数是反映传热速率的一个重要参数. 在本研究中，固/液界面处的传热系数HTC(Heat transfer coefficient)计算如下：

(4)

其中Ts是固体表面的温度，Tl是液态氩的温度. 混合润湿性表面上液氩的HTC如图10所示. 对于hc=1.5 nm，液氩的沸腾时间较晚，由于较大的分子间作用力，纯亲水表面的HTC在蒸发阶段略有增加. 随着β的增加，疏水部分增加，成核时间变短，液层中出现更多的蒸汽，降低了传热性能，液氩的HTC越来越低.hc=2.5 nm时，HTC的变化趋势与hc=1.5 nm时相似，不同的是，液氩的HTC先略有上升，然后缓慢下降，这是由于沸腾时间加快，固液之间产生蒸汽膜，降低了传热效果.

4 结 论

在本文中，采用分子动力学方法构建了疏水-亲水混合柱纳米结构壁对池沸腾的影响，讨论了疏水占比为0、33%、53%和73%时，两种圆柱高度下爆发沸腾的起始温度和时间. 此外，还深入研究了具有混合亲水性和疏水性的圆柱形纳米结构对爆发沸腾的影响. 得出的结论总结如下：

(1)与纯亲水的纳米结构壁面相比，增大疏水部分占比和圆柱高度后可以降低爆炸沸腾的起始温度并使发生沸腾的时间提前.

(2)通过观察不同配置壁面的沸腾过程快照，发现增加疏水占比将改变气泡出现的位置，不再只是从底部产生，而是转变为亲水疏水交接处或者圆柱顶端. 证明混合润湿性纳米结构有利于气泡成核，促进爆炸沸腾.

(3)当疏水占比相同时，柱高为2.5 nm的混合润湿壁面的爆炸沸腾起始温度低于柱高为1.5 nm的混合润湿壁面. 这是由于增大了与液氩之间的接触面积，在保持亲疏水比例不变的情况下，进一步放大了混合润湿性纳米结构的影响.

(4)随着疏水性在混合润湿性纳米结构上所占比例的增加，体系爆发沸腾发生的速度加快，使得液氩在相变过程中需要从壁面吸收的能量减少，平均热流降低，液氩的HTC降低，导致沸腾后传热效果不佳.