针对高分子刷构象转变的自振荡模型

郭秀珍， 李康睿， ， 李九智， 赵新军， ， 蒋中英

1）伊犁师范大学微纳电传感器技术与仿生器械实验室，新疆伊宁 835000；2）伊犁师范大学物理科学与技术学院，新疆凝聚态相变与微结构实验室，新疆伊宁 835000；3）新疆维吾尔自治区人民医院泌尿中心，新疆乌鲁木齐 830001

刺激响应性高分子刷在施加外部触发因素（如热、光和pH 值）时表现出独特的物理化学性质变化［1-3］，因此被应用于生物传感、医疗和组织工程等领域［4］.近年来，设计新型自振荡高分子刷成为表面材料设计领域的热点之一［5-6］.与大多数传统的二元（开/关）刺激响应刷相比，在恒定的外部条件下，自振荡高分子刷会自主地表现出构象的振荡变化特性，因此在封闭空间中具有独特的应用［7-8］.

由自振荡高分子接枝而成的自振荡高分子刷，可实现从化学振荡到机械振荡的能量转换［9］.其中，改性自振荡高分子链的一种典型的化学结构是聚异丙基丙烯酰胺（N-isopropylacrylamide，PNIPAM）和三（2，2"-联吡啶）钌（Tris（2-2"-bipyridine）ruthenium，Ru（bpy）3）的共聚物.Ru（bpy）3 催化是一种被称为Belousov-Zhabotinsky（BZ）反应［10］的振荡化学反应.在BZ 反应期间，高分子链经历循环还原-氧化反应，由于自振荡高分子的亲水性变化取决于Ru（bpy） 3 的氧化还原，高分子链在无催化剂的BZ 反应溶液中产生自主的、周期性的溶胀-塌缩转变.此外，BZ 反应物在自振荡高分子刷中的反应扩散，允许刷的高度变化以化学波的形式传播，为用作流体控制或纳米传输装置提供了可能［11］.作为利用自振荡高分子刷设计自主功能表面的首个成就，MASUDA等［12］采用表面引发的原子转移自由基聚合（surface-initiated atom transfer radical polymerization， SI-ATRP）法在玻璃基板上制备了自振荡高分子刷，并在高分子刷层中观察到了传播的化学波.基于这些发现，HOMMA等［13］制备的自振荡高分子刷有效实现了在高分子刷中BZ 反应诱导的稳定自振荡.

在高分子刷的自振荡过程中，催化剂的振荡氧化还原变化会引起高分子链亲水/疏水变化，导致自振荡高分子刷构象转变呈现出更丰富的动力学行为［14］.深刻理解自振荡高分子刷构象转变呈现的动力学，对设计相关材料非常重要.相比传统的高分子刷，自振荡高分子刷的构象可周期性切换.因此，高分子刷构象转变的自振荡的动力学与非振荡的均聚物高分子刷显著不同，也不同于高分子凝胶体系的化学振荡.现有研究高分子刷构象转变行为的理论模型［15-18］都基于平衡态统计，无法获得高分子刷自振荡的动力学特性（高分子刷自振荡动力学远离平衡态）.另外，关于高分子体系化学振荡的理论研究目前也只是考察高分子凝胶的自振荡效应［19-20］，并不能获得高分子刷自振荡导致化学波形成，且高分子凝胶构象转变的自振荡行为远不同于高分子刷.迄今未见定量研究高分子刷的自振荡与化学波的理论模型，因此无法获得自振荡的高分子刷随时间演化的动力学特性，也不能预言其新的动态结构改变特性.建立动态理论模型，考虑振荡行为的物理化学参数（包括自催化反应的速率常数、活化剂的扩散常数以及反应和扩散的活化能）调控特性，所得结果将有助于后续开发新的应用.本研究通过建立基于扩散动力学的高分子刷构象转变空间动力学模型，研究自振荡高分子刷的动力学特性，进而预言新的构象转变行为，为设计自振荡高分子刷纳米材料提供参考和新方案.

1 高分子刷构象转变空间动力学理论模型

将高分子链均匀地接枝在培养基表面并形成刷状结构，高分子刷构象转变在垂直于培养基表面（x-y平面）的方向（即z≥ 0 方向）.高分子刷构象的周期性转变模型如图1.由图1 可见，浸没在溶液（假定溶剂为水）中的高分子刷在微环境因素刺激作用过程中沿着z方向塌缩或溶胀.

图1 高分子刷构象的周期性转变模型Fig.1 Schematic diagram of self-oscillation of polymer brushes.

高分子刷由塌缩转变为溶胀的过程，可模型化为高分子链在z方向的扩散.由于高分子链内的单体扩散直接决定了其与溶液分子的相互作用也具有相应的扩散性质，且很大程度上决定了高分子刷的构象转变特性，因此，基于扩散动力学［21］，浸没在溶液中的高分子刷塌缩和溶胀的动力学方程分别为

式（1）等号右边的第1 项描述了高分子链单体的扩散性.其中，ϕ(t，z)为t时刻高分子刷内高分子链单体在z处的体积分数；D为扩散系数.式（1）等号右边的第2项描述了溶液中的分子与高分子链单体间的相互作用，其源于高分子刷在自振荡过程中，高分子链单体会由于催化反应导致亲水/疏水性的改变，基于大分子催化反应特性，该相互作用可表示为

其中，σ为高分子链单体与溶液中分子间的塌缩反应强度，暗含了单位时间内的催化反应特性；χ（t，z）为Flory-Huggins 相互作用势函数（记为FH 势函数）［22］，表示溶液中的分子与高分子链单体间的相互作用；K为高分子链单体扩散速率为时的相互作用势.

式（1）等号右边第3 项描述了高分子链单体在溶液中扩散的抑制效应.高分子链定域体积分数的增大，会使得高分子链单体与溶液中分子间的相互作用减弱，减缓高分子链单体的扩散性.该项抑制效应为

其中，μ为扩散减缓率.

式（2）等号右边第1 项描述了因高分子链单体的扩散性而导致的溶液中分子与高分子单体间化学反应的空间扩散性（即化学波效应），这种扩散直接决定了溶液中的分子（溶剂分子或催化剂分子）与高分子链单体间的相互作用沿着高分子链方向的传导.由于高分子单体扩散速率增加，会导致高分子单体与溶液中分子间的化学反应几率减小，因此，传导系数R= 1/D.

式（2）等号右边第2 项描述了因溶液中的分子与高分子链单体间的催化化学反应导致的高分子单体亲水/疏水性的转变，对高分子链单体与溶液中分子间的相互作用扩散的增强和减弱作用.该效应可表示为

其中，κ为高分子链单体与溶液中分子间的溶胀反应强度，暗含了单位时间内催化化学反应导致的高分子单体亲水/疏水性的转变性.

式（2）等号右边第3 项描述了因高分子链单体与溶液中分子间的相互作用对催化化学反应的抑制效应，进而影响溶液中的分子与高分子链单体间的相互作用的传导，可表示为

其中，ε为高分子链单体与溶液中分子间的相互作用强度，暗含了催化反应导致的单位时间内，溶液中的分子与高分子链单体间的相互作用的传导特性.本研究设定z= 0 为培养基表面边界，z=L为接枝的高分子链在距离垂直培养基表面方向所能到达的最大距离.通过对比已有实验结果［5，8，13-14］，确定本研究模型参数D= 1.26、μ= 0.08、σ= 0.25、K= 0.2、κ= 1.

2 仿真结果与讨论

BZ 反应伴随着催化剂的自发氧化还原振荡，其产生的时间节律或时空模式（称为化学波）作为耗散结构之一［23］.基于方程（1）和（2），并选取不同的参数与边界条件，可描述不同化学、物理特性的高分子刷构象转变的自振荡的动力学行为（图2）.

图2 高分子刷体积分数与 FH 势函数随时间和空间的变化关系 （初始条件为φ（0， z） = 0.35和χ（0， z） = 0.01； 边界条件为φ（t， 0） = 0.35、 χ（t， 0） = 0、 ∂ϕ(t，L)/∂z = 0和∂χ(t，L)/∂z = 0） （a）高分子刷体积分数的时空分布； （b）FH势函数的时空分布； （c） z = 20 nm与z = 36 nm处高分子刷体积分数随随时间演化呈周期性振荡； （d） z = 20 nm与z = 36 nm处FH势函数随时间演化呈周期性振荡； （e）t = 20 s与t = 36 s时高分子刷体积分数的空间分布； （f）t = 20 s与t = 36 s时， FH势函数的空间分布Fig.2 Spatial and temporal distribution of polymer brush volume fraction and FH potential function. The initial conditions are φ(0, z) = 0.35, χ (0, z) = 0.01, and the boundary conditions are φ(t, 0) = 0.35, χ (t, 0)=0, ∂ϕ(t, L)/∂z = 0, ∂χ(t, L)/∂z = 0. (a) The spatio-temporal distribution of volume fraction of polymer brushes. (b) The spatio-temporal distribution of FH potential function. (c) The volume fraction of polymer brushes exhibits periodic oscillations over time at z = 20 nm and z = 36 nm. (d) The FH potential function exhibits periodic oscillations over time at z = 20 nm and z = 36 nm. (e) Spatial distribution of volume fraction of polymer brushes at t = 20 s and t = 36 s. (f) Spatial distribution of volume fraction of FH potential function at t = 20 s and t = 36 s.

由图2（a）和（c）可见，随着时间演化，高分子刷的体积分数呈周期性动态演化特性，表明高分子刷具有周期性的塌缩-溶胀构象转变行为，导致刷内高分子链单体定域体积分数随时间周期性演变.在垂直培养基表面方向，高分子刷内高分子链呈蜷缩-伸展的周期性转变，表现为高分子刷构象转变的自振荡.图2（e）中，当t= 20 s 与t= 36 s 时，塌缩态的高分子刷体积分数呈类似抛物线分布；当t= 96 s时溶胀态的高分子刷体积分数则在垂直培养基表面方向均匀分布.这与分子场和自洽场平衡态［16-18］理论模型获得的高分子刷塌缩和溶胀态体积分数分布一致.可见，高分子刷的塌缩-溶胀构象转变的动态特性遵守扩散动力学规律.

高分子刷构象转变的自振荡源于高分子链单体的化学振荡反应，伴随着催化剂的自发氧化还原振荡，FH势函数也呈现周期性动态演化特性，如图2（b）和（d）.这表明高分子单体水合性由于化学振荡反应，产生时间节律性，其周期性与刷内高分子链出现的蜷缩-伸展的周期性相同，但存在振荡的时间差.正是高分子单体水合性的化学振荡反应，调控了高分子刷构象转变的自振荡，作为耗散结构之一，使其产生时间节律或时空模式.由图2（f）可见，在培养基表面附近溶剂和催化剂小分子由于很难进入，成为游离溶剂和催化剂小分子的耗尽层.随着反应的进行，在高分子刷溶胀区域，高分子单体与溶剂和催化剂小分子呈现出充分的化学反应，且反应程度随时间延长而逐渐饱和.高分子单体密度较大的空间，致密的单体导致溶剂分子很难进入到单体较密的区域，溶剂与单体间的相互作用被单体屏蔽，表现为高分子单体与溶剂分子排斥FH 势增强，水合性减弱.然而，在距离培养基表面较远的地方，分布了较为伸展的高分子链，致使高分子单体与溶剂和催化剂分子化学反应充分，FH 势明显改变，水合性得到了改善.高分子链的舒展使得溶剂和催化剂分子与高分子单体接触的几率增大，极大地改变了高分子单体与溶剂和催化剂分子间的水合作用，增强了高分子单体的水合性，高分子链溶胀.这表明，通过改变培养基表面属性，使溶剂和催化剂分子可进入距离培养基较近的单体密度较高区域，从而改变高分子刷化学振荡的稳定性［24］.HOMMA等［24］报道了一种新型自振荡的仿生高分子刷，在BZ 反应期间，Ru（bpy）3 催化的共聚物刷经历循环还原-氧化反应，该氧化还原反应改变了自振荡高分子的亲水性.

高分子刷构象转变的自振荡，还会改变高分子刷的高度.为定量研究高分子刷构象转变的周期性，可考察高分子刷平均高度（高度）随时间的演化.高分子刷的平均高度［25］为

式（8）反映了高分子链的伸展程度，伸展的高分子刷链数越多平均高度越大；反之，蜷缩的高分子刷链的数目越多则平均高度越小.高分子刷平均高度的变化明显反映出高分子刷刷构象的转变.

图3给出了高分子刷平均高度随时间的变化关系.其中，L为高分子链长.由图3 可见，在高分子刷构象转变过程中，高分子刷的平均高度随时间呈周期性演化，即随着时间的演化，高分子刷呈现出塌缩-溶胀的构象转变行为.HOMMA等［13］通过实验发现，在适当的接枝密度条件下，伴随着催化剂的自发氧化还原振荡，高分子刷的高度出现大幅度塌缩-溶胀的构象转变行为.这是由于在由适当的接枝密度与较长的高分子链接枝而成的高分子刷溶胀过程中，在垂直培养基表面方向上，高分子链可以分布在更大尺度的空间.比较图3（a）和（b）还可发现，较长的高分子链长会导致高分子刷的平均高度随着时间呈现周期性演化的振幅增加现象.由于适当的接枝密度与较长的高分子链长，高分子刷内分布了较多的单体密度，高分子刷在塌缩-溶胀过程中，在垂直培养基表面方向上，化学振荡则可以在更广阔的时空尺度内进行.因此，不同时空边界产生的周期性行波，致使高分子刷高度振荡振幅随着高分子链长的增加而增长.研究发现，高分子链长的改变也会在很大程度上影响高分子刷的化学振荡特性［10］.此外，BZ 反应物在自振荡高分子刷上的反应扩散允许厚度变化以化学波的形式传播［13，22］.当高分子构象转变与BZ 反应耦合时，高分子刷通过亲水性和疏水性相互作用作出反应，导致刷的高度发生变化，从而引起机械功［26］.随后，化学能和机械能的转换自动发生，形成沿着链“传递”的波动，从而使高分子链呈现出循环溶胀-塌缩的构象转变［27-28］.

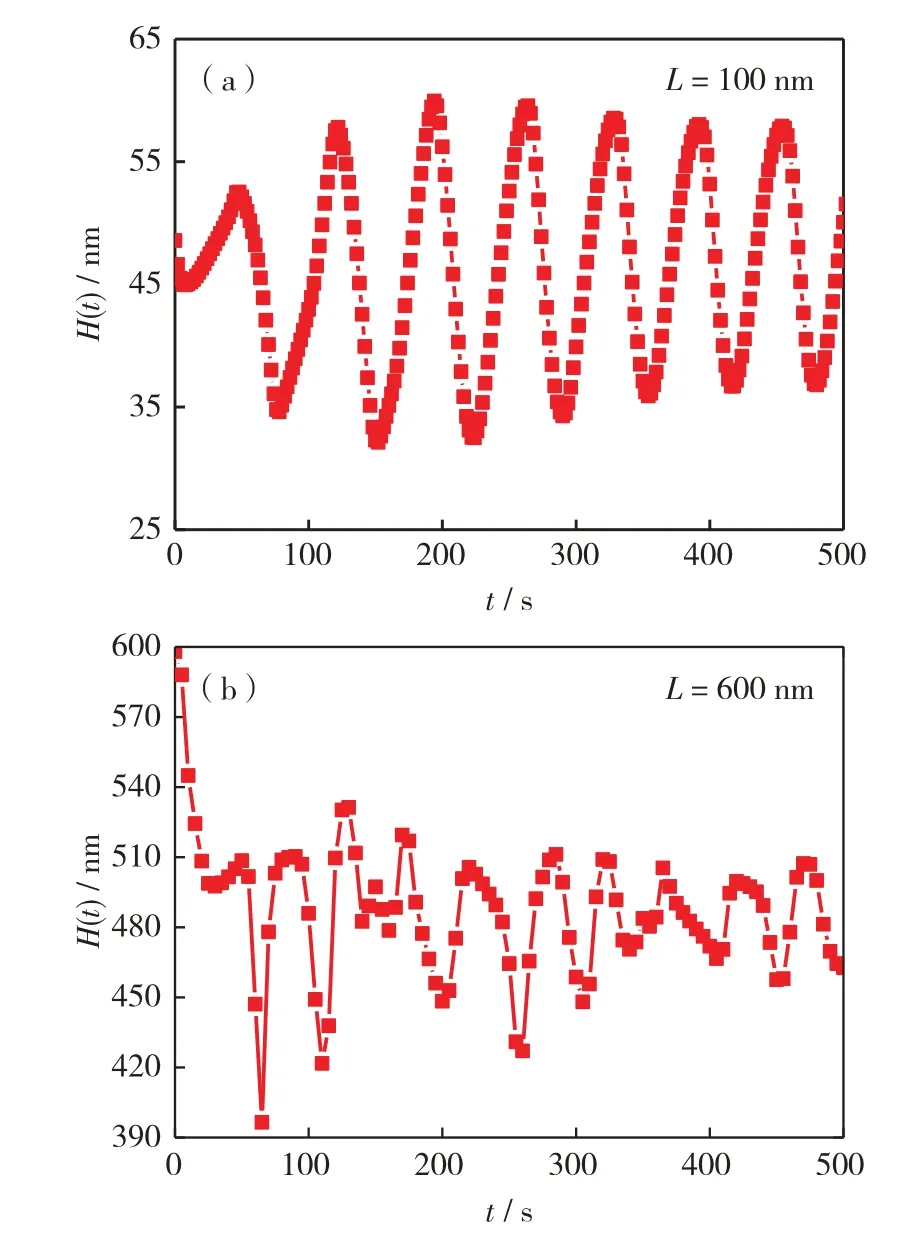
图3 高分子刷平均高度随时间的变化（参数设置与图2相同） （a）L = 100 nm；（b）L = 600 nmFig.3 The time evolution of height of the polymer brushes (All parameters are same as those in Fig.2.). (a) L = 100 nm and(b) L = 600 nm.

图4 给出了高分子刷体积分数与FH 势函数的时空分布.由图4 可见，高分子刷体积分数与FH势函数的时空分布呈化学波振荡模式，表明高分子刷的构象随时间和空间呈周期性演化，高分子刷体积分数的空间分布呈波动传播特性（图4（a）至（c）），振荡周期约为50 s.HOMMA等［24］通过实验制备的自振荡高分子刷展现了周期为20 ～ 60 s周期振荡行为，且观测到振荡以化学波的形式传播.这种波动性源自高分子单体的BZ 反应，且是一种化学振荡反应，导致FH 势函数也呈现出随时间演化的周期性与空间分布的波动特性.伴随着催化剂的自发氧化还原振荡，高分子刷自振荡产生时间节律或时空模式（化学波）作为耗散结构之一.高分子刷体积分数的空间分布呈波动特性，表明高分子刷体积分布是空间不均匀的，这种不均匀分布在垂直培养基表面的分布又具有空间周期性，表明在高分子刷内出现结节状结构，如图4（e）插图.本研究团队前期研究也发现，PNIPAM 球面刷系统中，由于PNIPAM水合性的改变和SCN-效应，会导致PNIPAM呈现出额外的疏水作用和静电稳定性增强，致使PNIPAM刷出现垂直相分离的结节结构，原因是高分子单体伴随着催化剂的自发氧化还原振荡［25］.HOMMA等［24］研究发现，引入增强金属催化剂并保持接枝高分子附近中间产物的有效浓度，有助于BZ 反应期间的稳定振荡.在高分子刷内高分子单体的疏密性呈周期性空间分布，在催化剂的自发氧化还原振荡化学应下，这种疏密性会沿着链方向（z方向）扩散传播，形成高分子刷内的化学波［23，26］.

图4 高分子刷体积分数与FH势函数的时空分布呈化学波振荡模式（初始条件为φ（0， z） = 0.01、 χ（0， z） = 0.01， 边界条件为ϕ(t，0) = 0.01、 χ(t，0) = 0、 ϕ(t， L) = 0.5、 χ(t，L) = 0.5） （a） 高分子刷体积分数的时空分布； （b） FH势函数的时空分布；（c） z = 200 nm处， 高分子刷体积分数随随时间演化呈现周期性振荡； （d） z = 200 nm处， FH势函数随时间演化呈周期性振荡；（e） t = 20 s时高分子刷体积分数的空间分布； （f） t = 20 s时， FH势函数的空间分布Fig.4 The spatial and temporal distribution of polymer brush volume fraction and FH potential function shows a chemical wave oscillation mode. (The initial conditions are ϕ(0, z) = 0.01, χ(0, z) = 0.01, and the boundary conditions are ϕ(t, 0) = 0.01,χ(t, 0) = 0, ϕ(t, L) = 0.5, χ(t, L) = 0.5.) (a) The spatiotemporal distribution of volume fraction of polymer brushes. (b) The spatiotemporal distribution of FH potential function. (c) The volume fraction of polymer brushes exhibits periodic oscillations over time at z = 200 nm. (d) The FH potential function exhibits periodic oscillations over time at z = 200 nm. (e) Spatial distribution of volume fraction of polymer brushes at t = 20 s. (f) Spatial distribution of volume fraction of FH potential function at t = 20 s.

BZ 反应导致化学振荡会令高分子链单体因催化反应改变其亲水/疏水性.图5给出的高分子单体催化反应特性θ（t，z）的时空分布特性（参数设置与图4 相同）.由图5 可见，高分子单体催化BZ 反应呈现波动特性.由于催化剂的自发氧化还原振荡，高分子单体的BZ 反应也产生化学波，其在刷内的扩散也以化学波形式传播，这是耗散结构的起源之一.这种BZ 反应化学波的形成是在高分子刷系统产生耗散结构，该系统包含催化剂、水分子和高分子单体等多层次的组分.自振荡高分子刷系统通过催化反应，使得高分子刷中的高分子与外界进行化学物质与能量的交换，令高分子刷构象转变远离平衡的状态，在涨落的触发下，高分子刷内的高分子链不断从蜷缩变为伸展从而形成时空结构.这种耗散结构是由于远离平衡态的高分子刷系统在与外界交换物质和能量过程中，通过链内单体作用产生自组织，使系统出现塌缩-溶胀构象转变的动态特性，这种构象转变完全是高分子刷内的高分子链在催化反应作用下与外界交换物质和能量的结果，可令高分子刷系统从高熵转换到低熵状态，这与文献［25］中高分子刷构象转变过程中熵增加驱动的自组织不同.可见，自振荡的高分子刷可改变BZ反应模式.研究表明，BZ 反应可在聚合物刷内部被稳定地诱导，其响应性可以根据自振荡高分子刷的表面设计进行调节［23，29］.

图5 高分子单体催化化学反应特性θ（t， z）时空分布呈化学波振荡模式（参数设置与图4相同） （a） z = 5 nm时θ（t， z）随时间演化特性； （b） t = 50 s时θ（t， z）的空间分布； （c） θ（t， z）的波动性.Fig.5 The time-space distribution of catalytic chemical reaction, θ(t, z). The characteristics of polymer monomers presents a chemical wave oscillation mode. (All parameters are the same as those in Fig.4.) (a) Temporal evolution of the level of θ (t, z) at z = 5 nm. (b) Spatial distribution of volume fraction of θ (t, z) at t = 50 s. (c) The fluctuation characteristics of θ (t, z).

结 语

HASEGAWA 等［22］的动力学平均场理论，无法获得自振荡的高分子刷化学波传播特性.本研究基于扩散动力学理论模型，考虑高分子刷自振荡时空传播动力学，建立了新的模型研究高分子刷构象转变的自振荡的动态特性.研究发现，在垂直培养基表面方向，高分子刷呈塌缩-溶胀的周期性转变，高分子刷构象转变具有自振荡现象.这是由于高分子单体氧化还原反应的自振荡，导致FH 势函数也呈现周期性动态演化特性.伴随着BZ 反应的时空波动性，FH 势函数和高分子刷体积分数还表现出波动特性.这种波动性源于高分子单体的BZ反应，波动产生时间节律或时空模式作为耗散结构之一.高分子刷体积分数的空间分布呈现波动特性，会导致刷内高分子单体体积分布具有空间不均匀性，进而在高分子刷内出现结节状结构［25］.BZ 反应导致的化学振荡，也以化学波的形式在高分子刷内扩散，这是耗散结构的起源之一，且自振荡高分子刷还可改变BZ反应模式.

本研究模型建立在扩散动力学基础之上，高分子刷构象转变的自振荡的动力学特性，完全是由于溶剂和催化剂BZ 反应导致的高分子刷构象的周期性改变，但这并未考虑高分子链的弹性、溶剂渗透压和pH 值的耦合调控效应［27，31］.考虑多因素耦合的BZ 反应，更全面地描述高分子刷构象的周期性改变和BZ 振荡的化学波特性，将是一个具有挑战性的问题.本研究考察的较长的高分子链可看作高斯链，其单体的扩散可看作无规行走，而弹性效应与渗透压效应可以忽略.因此，对于长链高分子单体的化学振荡，以及化学波的形成，主要是由于溶剂-高分子单体BZ反应导致的高分子刷构象的周期性改变.本研究理论结果符合实验观测结果［23-24］，基于所提理论模型，确定了高分子刷构象转变的化学波特性，可为表面材料设计，以及自振荡高分子刷在封闭空间中具有更独特的应用提供指导.