基于模糊控制的PWM整流器电压调速策略

黄自鑫 ， 汪伟 王乐君

1）武汉工程大学电气信息学院，湖北武汉 430205；2）南开大学人工智能学院，天津 300071；3）武汉工程大学智能机器人湖北省重点实验室，湖北武汉 430205；4）武汉纺织大学湖北省数字化纺织装备重点实验室，湖北武汉 430200；5）重庆市复杂系统与仿生控制重点实验室，重庆邮电大学，重庆 400065

随着科技的发展，人们对于机器人［1］的研究越发成熟.其中，考虑到能源能耗的要求，基于欠驱动结构和特性设计机器人的方式备受关注.欠驱动指控制输入个数少于系统自由度个数的系统［2-4］，以此来减少系统能源的消耗.自由度则是描述系统运动状态的独立变量个数［5-6］.在生产和科研活动中有许多的欠驱动系统［7-8］，如板球系统［9］、倒立摆系统［10］、欠驱动机械臂［11］和空间飞行器［12］等.

基于欠驱动系统的研究成果［13］，本研究将欠驱动和自由度概念运用于电力电子系统中，分析三相电压型脉宽调制（pulse width modulation， PWM）整流器电力电子系统的特性.三相PWM 整流器具有网侧功率因数高和谐波含量少等特点［14］，已被广泛运用于微电网、电机驱动调速和大功率直流充电等领域［15］.PWM 整流器需要实现电网侧电流的正弦化和直流侧电压快速稳定［16］两部分控制目标.传统PWM 整流器控制系统所采用的双闭环比例积分（proportional integral， PI）控制策略，因缺少对无功电流零动态稳定性分析，对PWM 整流器系统的控制效果较差［17］.而电压外环的控制策略会直接影响到PWM 整流器的电网侧抗扰动能力和直流侧电压响应速率等性能指标［18］，所以针对电压外环的控制策略是非常值得研究的.

针对PWM 整流器系统的数学模型，利用其欠驱动特性，可将该控制系统划分为驱动子系统和欠驱动子系统，对该PWM 整流器系统的状态变量作为欠驱动变量的可行性进行分析.利用反馈线性化［19］对驱动子系统进行内环滑模控制器设计，通过分析PI 参数变化对PWM 整流器系统性能的影响，提出符合此系统的模糊规则，设计模糊控制策略的电压环控制器.通过对压环和电流环两部分控制器的设计来优化传统PI 控制策略的控制效果，从而改善PWM 整流器控制系统的动态和稳态性能，并通过对比仿真实验对本研究设计的控制策略进行验证.

1 建模与分析

1.1 数学模型

三相电压型PWM 整流器的电路结构拓扑图如图1.其中，ea、eb和ec分别为三相交流输入电压；ia、ib和ic分别为交流输入电流；SK和S"K均为开关状态量，K分别为a、b、c相；L和C分别为交流侧滤波电感值和直流侧滤波电容值；R为交流侧等效电阻阻值；RL为负载电阻阻值；iL为负载电流；u0为直流侧电压值.

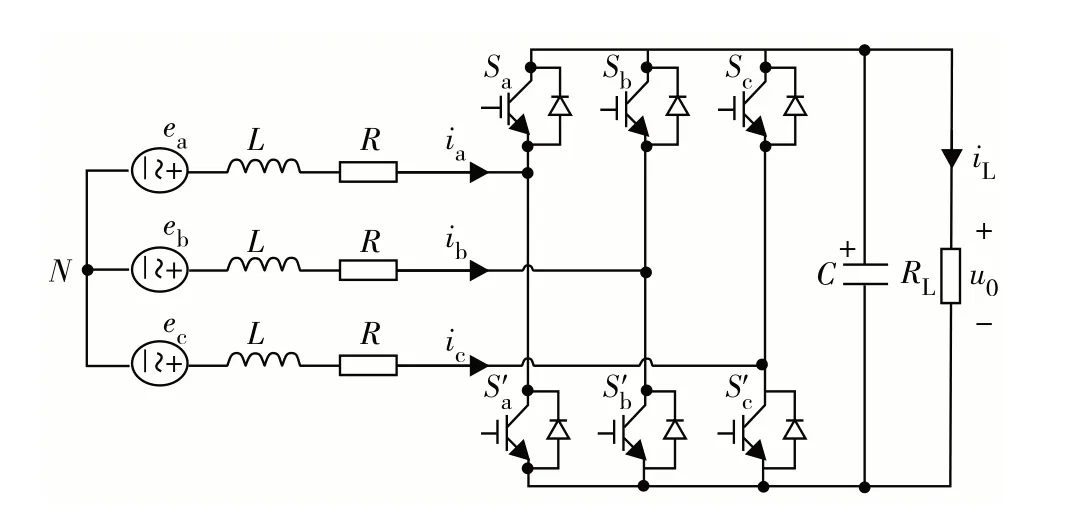
图1 PWM整流器电路结构拓扑图Fig.1 PWM rectifier circuit structure topology diagram.

定义开关函数为

其中，K可取a、b或c相.

根据三相电压型PWM 整流器的电路结构拓扑图，利用基尔霍夫定律，建立电压回路方程和电流节点方程组为

其中，ω为旋转坐标轴下的角速度.

1.2 特性分析

由式（2）可得PWM整流器的状态空间形式的数学模型为

其中，为ia的微分量；̇为ib的微分量；为ic的微分量；Sa、Sb和Sc分别为绝缘栅双极型晶体管（insulated gate bipolar transistor， IGBT）开关的状态量；A、B和C为输入系数矩阵，且

由式（4）的空间状态表达式可得出，矩阵B的行列式为

由于系统输入系数矩阵的行列式为0，得出控制输入的系数矩阵B的秩rank（B） ＜ 3，而从系统状态空间表达式中可得出系统自由度系数矩阵A的秩rank（A） = 3，所以可得出本研究的PWM 整流器控制系统控制输入量少于系统自由度数量，可从欠驱动的角度来对其控制策略进行研究.

1.3 控制策略分析

从PWM 整流器的特性分析中得出其控制系统可作为一个欠驱动控制系统，因此，可利用欠驱动特性，将PWM 整流器控制系统分为驱动子系统和欠驱动子系统，再通过选择两个控制子系统的控制变量来确定本研究的控制策略.

通过在qd同步旋转坐标系下进行等功率变换，得到PWM 整流器的电网侧和直流侧的瞬时功率平衡关系为

式（5）反映的是PWM整流器能量变化的本质特征，得到id、iq和u0的内部动态（零动态）方程.欠驱动变量的选择要以实现PWM 整流器的控制目标为依据，PWM 整流器的控制目标需要实现直流侧电压u0收敛于给定电压ur，且iq收敛于给定电流idr= 0（即实现电网侧单位功率因数控制）.本研究以u0作为欠驱动变量来进行控制策略研究，并验证其可行性.

令式（5）中的id=idr，且iq= 0，则可得到以u0为欠驱动变量的系统零动态方程为

从式（6）可见，要使u0收敛到给定值ur，即只需对id和iq进行直接控制，使id收敛到给定值idr，且iq收敛到0，即可实现对u0的间接控制.

由式（3）可得到u0和id之间的传递函数为

由此可以进行对电压环控制器的设计.该控制器的输入为给定值ur，控制器的输出作为id的给定值idr，从而间接实现对u0的控制.所以，以u0为欠驱动变量的方案是可行的.

最终PWM 整流器的控制策略如图2.选择u0为欠驱动变量，设计电压外环控制器，选择id和iq为驱动变量，设计电流内环控制策略.

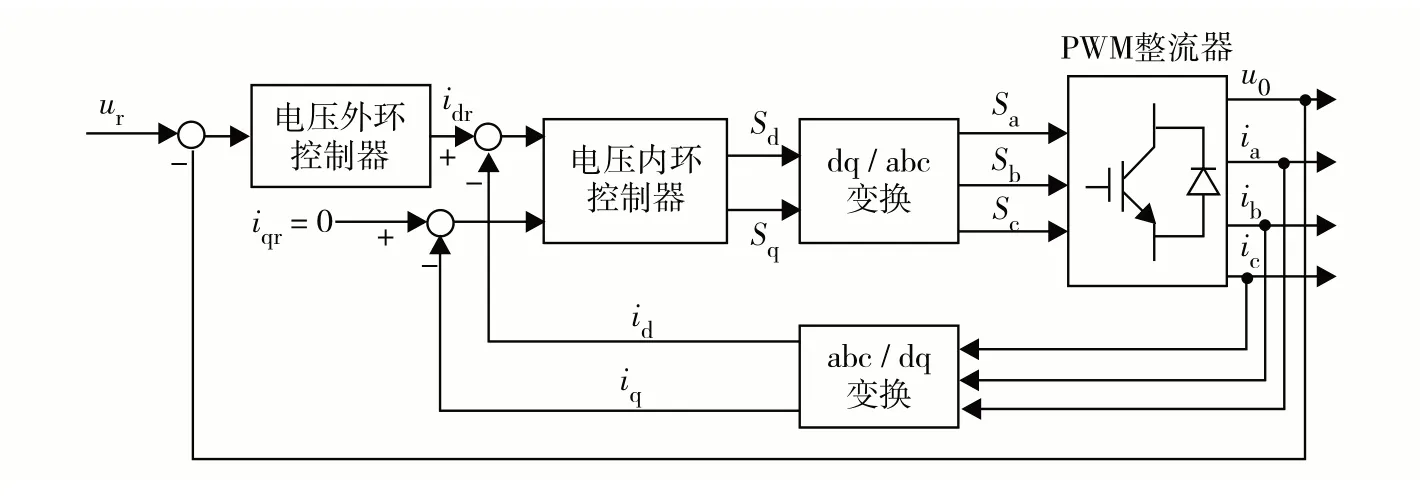
图2 PWM整流器的双闭环控制系统结构Fig.2 Structure of double closed-loop control system for PWM rectifier.

2 PWM整流器控制器设计

2.1 电压外环控制器设计

PWM整流器的电压外环通常采用经典PI控制，但是此方法很难保证系统较好的动态性能，而且积分系数会直接影响u0的稳态时间.因此，针对这一问题，结合欠驱动变量u0，利用式（7）所给出的电压电流关系设计电压外环控制器.在电压外环控制上，采用模糊PI 控制，使其比例和积分系数随着误差的改变而改变，从而提升系统的动态性能.

通过上述外环电压控制分析，可得出PI 参数控制输入与系统响应结果之间的关系，进而得出两条基本规则：① 若Δe减小，则kp增大，ki减小；②若Δe增大，则kp减小，ki增大.

令直流侧电压u0的系统误差为Δe，则Δe=ur-u0.其中，ur为给定电压值.定义模糊控制的输入/输出模糊集为Δe=｛NB，NM，NS，ZO，PS，PM，PB｝；kp= ｛NB，NM，NS，ZO，PS，PM，PB｝；ki=｛NB，NM，NS，ZO，PS，PM，PB｝.其中，NB 为负大；NM 为负中；NS 为负小；ZO 为0；PS为正小；PM为正中；PB为正大.

根据上述对PI 参数变化对系统响应结果的分析所得到的两条基本规则，进而确立以下7条模糊规则，如表1.

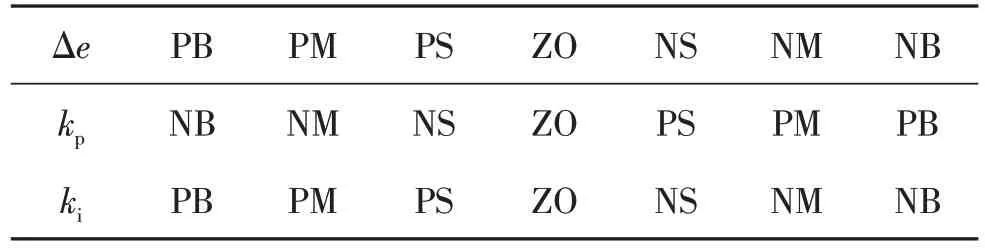
表1 模糊推理真值表Table 1 Fuzzy rule inference table

根据Δe的值，依据上述7条模糊规则，得到模糊输出kp和ki，再采用重心法［21］去模糊化，得到比例系数和积分系数的精确值和̂，最终设计的电压外环控制器为

其中，t为瞬时时间.

2.2 电流内环控制器设计

在电流控制设计上，针对驱动变量id和iq进行控制策略研究.由于传统PI 控制的电流环控制效果不好，且会出现PWM 整流器控制系统引起电流抖振现象.为优化电流环的控制效果，电流内环设计滑模控制，来减少系统引起的电流抖振.

定义变量

并设计滑模面S1=e1，S2=e2，则对S1和S2求导，并将式（3）中的前两式代入，可得

由于sgn函数会出现延时情况，导致PWM整流器理想开关特性无法实现，引起电流抖振.为减少电流环滑模控制所带来的抖振，采用饱和函数法引入sat函数代替sgn函数来抑制抖振现象，其数学表达式为sat(x)= min(max(x，-1)，1).

本研究采用等速趋近率

来验证两个滑模面的可达性，即

其中，K1和K2分别为趋近滑模面的速率.

由式（12）可见，两个滑模面满足广义可达条件，因此，最终得到电流内环控制率为

3 仿真实验

为验证所设计控制方法的有效性，在Matlab/Simulink 环境下进行仿真对比实验，分别在稳态运行和电压突变两种情况下进行实验，分析其稳定性和抗扰动能力.

PWM整流器控制系统采用如图2所示的双闭环结构.PWM 整流器控制系统的系统参数设置如表2.

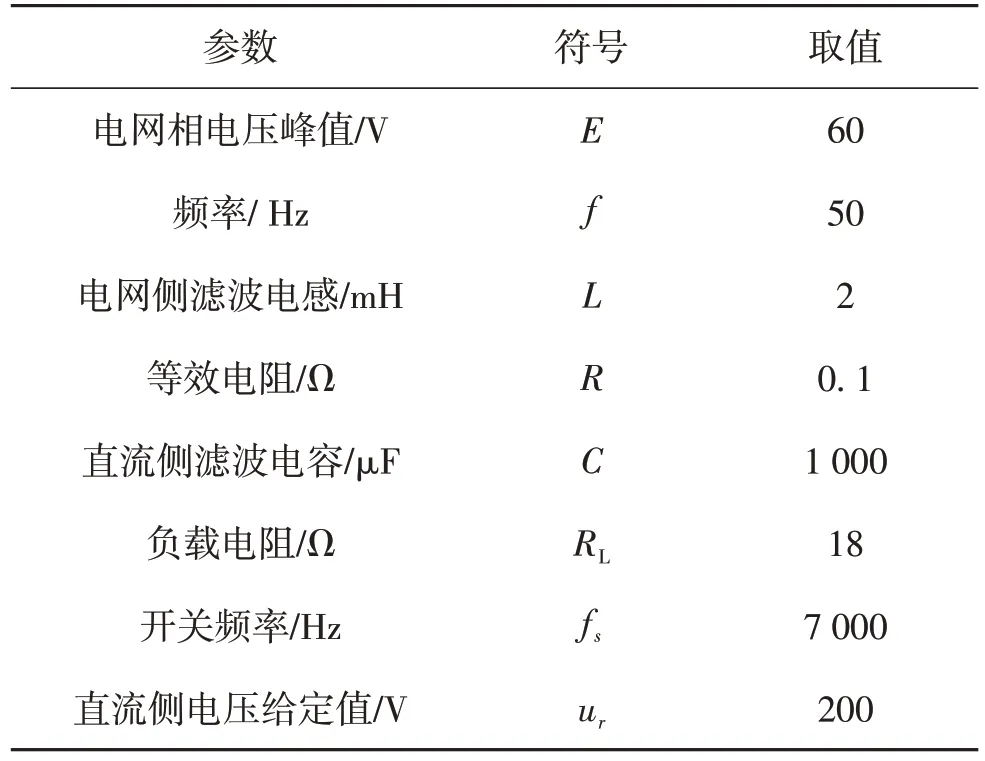
表2 PWM整流器的系统参数Table 2 System parameters of PWM rectifier

1）PWM系统稳态运行时

给定电压ur为200 V，PWM整流器控制系统仿真结果如图3至图6.

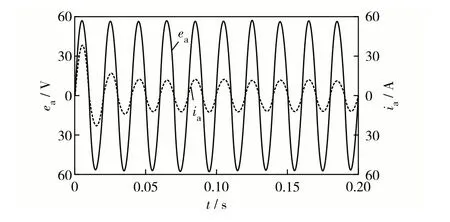
图3 模糊控制的ea和ia波形Fig.3 ea and ia waveforms with fuzzy control.

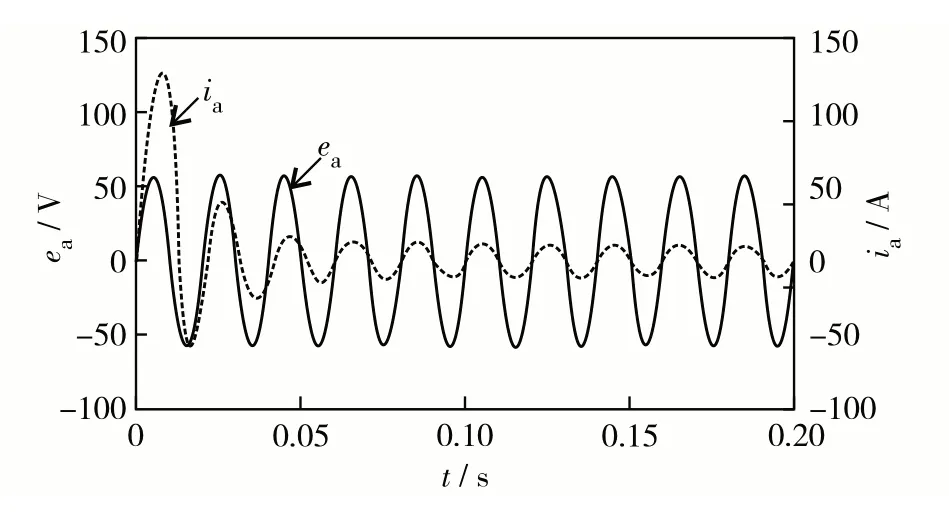
图4 PI控制的ea和ia波形Fig.4 ea and ia waveforms with PI control.

从图3 至图5 可见，在电网侧电流正弦化上，所提控制策略在0.04 s后基本稳定为正弦波，而PI控制要经过0.06 s后才能达到正弦稳定.在直流侧电压快速响应上，所提控制策略实现无超调快速响应，且在0.05 s后达到稳态值；PI控制则出现了超调现象，且在0.10 s后才能达到稳态值.可见，在实现电压快速调节目标上，本研究设计的模糊控制相较于传统PI 控制来说的动态性能和稳态性能更优，控制效果更好.

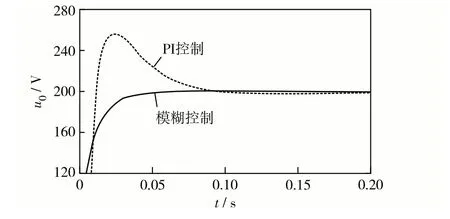
图5 直流电压响应波形Fig.5 DC voltage response waveforms.

图6 为PWM 整流器系统在稳态运行下两种方法的功率因数变化波形图.从图6可见，本研究所提的模糊控制策略的系统功率因数最高达到了0.99，且相对稳定，而传统PI 控制的系统功率因数最高达仅到0.99且不稳定.

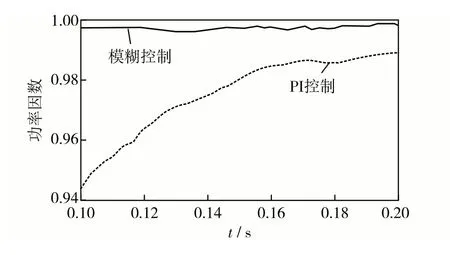
图6 系统功率因数Fig.6 System power factors. The solid line-represents fuzzy control, and the dashed line represents PI control.

2）PWM系统电压突变时

在系统运行0.15 s 时，设给定电压从200 V 突变为250 V 的情况下，PWM 整流器仿真结果见图7至图9所示.

图7 模糊控制的ea和ia波形Fig.7 ea and ia waveforms with fuzzy control.

从图7 和图8 可见，在针对电压突变情形下，本研究所提控制策略在电网侧电流正弦化上的稳定性更好.由图9可见，本研究所提控制策略在电压突变下只需0.03 s就达到了新的稳态，而传统PI控制需要0.10 s后才能达到新的稳态.

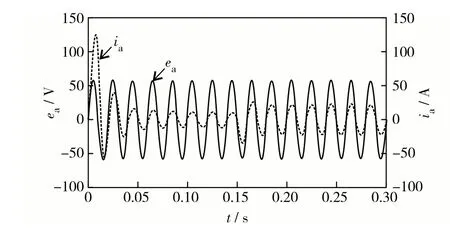
图8 PI控制的ea和ia波形Fig.8 ea and ia waveforms with PI control.

图9 直流电压响应波形Fig.9 DC voltage response waveforms. The solid line represents fuzzy control, and the dashed line represents PI control.

结 语

针对三相电压型脉宽调制整流器直流侧电压响应速率问题，对其欠驱动特性进行分析，提出电压外环模糊控制、电流内环滑模控制策略，并利用Matlab/Simulink 进行仿真验证所提控制策略性能.仿真实验结果表明，所提算法不仅在稳态运行时提高了直流侧电压的响应速率，而且在给定电压突变的情况下直流侧电压也能够快速响应，也提高了PWM 整流器系统的功率因素，提升了电源电压的利用率.最终的仿真结果验证了本研究所提控制方案的有效性.但是，本研究在针对系统运行过程中出现的电压抖震问题没有很好的解决，未来将集中在解决系统抖震问题和进一步系统的抗扰动能力，使其具有更强的应用前景.