谐波滤波器及小波去噪在水域电法中的应用

丁 丹，吴 双，昌彦君，吕淑娟，张 伟

(1.安徽省地质矿产勘查局 321地质队,安徽 铜陵 244033;2.中国地质大学 地球物理与空间信息学院,湖北 武汉 430074;3.贵州水利水电职业技术学院 土木工程分院,贵州 清镇 551416;4.武汉捷探科技有限公司,湖北 武汉 430011)

1 引言

电法勘探作为地球物理勘探方法之一,具有原理简单,勘探结果准确、直观等优点[1]。近年来,国内外实验及实践研究表明,水域电法具有较好的勘探效果,水的导电率能够传导较大的电流,对于解决水域范围内工程地质问题[2,3]、探明水底资源分布[4]及水下构造勘探[5]等领域具有较好的勘探效果。进行水域电法勘探,需要通过电极向水中注入电流,通过接收水中电流引起的电场变化来进行分析研究,该方法具有实现横向与纵向分辨率高,电极排列布置与移动简单,施工效率高且勘探速度快等优点。但在实际测量过程中,仪器供电往往使用50Hz交流电进行整流后输出,因此会导致采集到的信号耦合工频噪声,对探勘结果有较大的影响[6,7]。由于工频噪声无处不在且噪声强度大,在进行微弱信号采集中往往会淹没有效信号[8]。对工频噪声的特点进行分析,可以发现其能量主要集中在基频及其奇次谐波上[9,10]。为了抑制工频干扰,在电法勘探领域,对工频噪声的抑制有多种方法,如自适应滤波[11]、噪声估计法[12,13],这些工频噪声抑制方法都需要明确的工频谐波干扰参数,以获得可直接消除的噪声干扰,并且算法实现复杂,可能对水域电法勘探的实时性造成影响。

为了解决水域电法勘探存在工频噪声干扰的问题,本文结合谐波滤波器和小波去噪方法对水域电法采集过程中存在的工频干扰进行处理,提高探测数据的质量。之后,通过水槽模拟实验验证谐波滤波器及小波去噪在水域电法数据预处理中的可行性和有效性。

2 原理

2.1 谐波滤波器

谐波滤波器除了结构简单、适应性强以外,同时通过对参数的调整能够使工频噪声及其谐波有较大的衰减,同时有一定的带宽能够满足谐波干扰的基频扰动。本文的谐波滤波器的设计方法是基于梳状滤波器的原理。梳状滤波器是指按照一定频率间隔排列的通带或者阻带,只能允许特定频率的信号通过,而梳状滤波器一般可以视为不同中心频率窄带带通滤波器的叠加,根据文献[14]中提出的窄带带通滤波器传递函数:

(1)

式(1)中,N为滤波器的极点;j为虚数单位;ω0=2πf0为滤波器的截止频率;f0为工频噪声的中心频率,在研究工频噪声时取值为50 Hz。

由于工频干扰及其谐波具有倍频关系,根据式(1)使得工频干扰奇次谐波中心频率fa均设置为滤波器零点,通过零极点的设计将多个带通滤波器互相叠加,有

fa=(2i-1)ω0

(2)

式(2)中,i=1,2,...,n/2;n=f0/fs,fs为采样频率。

通过叠加后的梳状滤波器传递函数为式(3),即

(3)

将零点代入式(3)可以得到:

1+z-N=0

(4)

令

z=e-j2πn

(5)

有

1+e-j2πNn=0

(6)

e-j2πNn=-1

(7)

2πNn=π

(8)

所以有

图1 小波去噪流程Fig.1 Flow chart of wavelet denoising

(9)

同时,可以叠加窗函数对通带和阻带的纹波压制和衰减进行控制。常用的窗函数包括汉宁窗、海明窗和高斯窗。因为高斯窗能够调节带宽参数实现衰减频率的调节,因此被广泛使用[15]。

加入经过归一化的高斯窗参数a,取值范围为(0,1),该参数能够改善滤波器的性能,取值增大的同时,滤波器通带越平缓,对其他信号影响较小,但是衰减减小,因此高斯窗参数a的取值也要不同问题具体分析。通过引入高斯窗函数后,得到的梳状带通滤波器传递函数为,

(10)

根据式(11),使用全通滤波器减去梳妆带通滤波器得到谐波滤波器:

(11)

该滤波器的性能取决于高斯窗中高斯窗参数a的取值。

2.2 小波去噪

小波变换自提出就应用于噪声信号处理中,2011年,小波变换方法应用在高密度电法资料去噪研究中[16]。但是小波变化需要选择合适小波基函数,不同的小波基函数有着不同的分离噪声的效果,如果母小波选择不正确,容易导致信号发生畸变。

利用小波变换的水域直流电探测信号降噪包括三个步骤:首先,提取出有用的水域直流电探测信号特征;然后,在小波域进行滤波;最后,进行水域直流电探测信号重构就可以达到消噪的目的(图1)。直流电测深测量得到的电信号Ua为

(12)

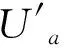
水域直流电探测信号特征提取的核心是在小波域中对探测信号进行分解。直流电探测信号通过选择一个小波基函数并给定分解的层次,对含噪电信号进行小波变换分解。每一层分解的结果是上次分解得到的低频信号再分解成低频和高频两个部分。

在小波分解过程中,将某一小波基函数做位移后,通过式(13)计算不同尺度下的基函数与原始水域直流电探测信号的内积,这样信号就被分解成一系列信号的叠加。

(13)

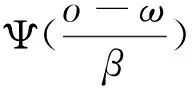
对于同样的探测信号,不同的基函数会得到不同的结果[17]。目前常用的基函数可以分成三类:Daubechies小波基,Symlets小波基和Coiflet小波基。Daubechies小波基具有较好的正则性,计算量小且去噪效果好,可以用于暂态噪声和瞬态噪声去除,但是随着小波阶数增加,Daubechies小波基计算量会增加,同时实时性变差;Symlets小波基是从Daubechies小波基演化而来,在连续性、滤波器阶数等方面与Daubechies小波基一致,但Symlets小波基有更好的对称性,能够降低在信号重构时对信号的失真;Coiflet小波基虽然是从Daubechies小波基演化而来,但牺牲了支撑长度来换取一定的对称性,一般不适用于实时信号处理[18,19]。

经过I层分解后,水域直流电探测信号Ua被分解为

(14)

式中,j=1, 2, ...,I;Yj为每层分解得到的估计小波系数;Mj(k)为第j层分解得到的低频水域电法探测信号,以测量信号为主(即有效电信号);Nj(k)为第j层分解得到的高频水域电法探测信号,以噪声为主。

随后,对分解得到估计小波系数进行阈值处理,利用硬阈值法来得到小波系数,通过一个滤波阈值实现噪声和有效信号的分离。阈值的选择将对去噪效果的好坏产生决定性的作用。人们依据水域电法电探测数据采样点数进行阈值选取,即长度对数阈值(式15)。

(15)

式中,λ为阈值;σ为首层小波分解系数绝对值的中间值。

硬阈值法(式16)可以尽可能地保留信号边缘等局部特征,使重构的信号具有更好的逼近性。若估计小波系数Yj小于λ,认为该系数由背景噪声引起,将其置零;若估计小波系数Yj大于等于λ,认为该系数由有效信号引起,保留该系数,并用于小波逆变换[20]。

(16)

在小波域完成电法探测信号与水域背景噪声的滤波分离后,就可以将分解后的信号进行重构,将新产生的Yj重新代入公式(14),所得到的Ua即为去噪后的有效信号。

将信号进行谐波滤波器和小波去噪处理后,利用公式(17)来计算信噪比评价去噪信号的优劣[21],

(17)

式中,x(n)为原始信号;y(n)为去噪后信号。

3 实际应用

3.1 实验平台

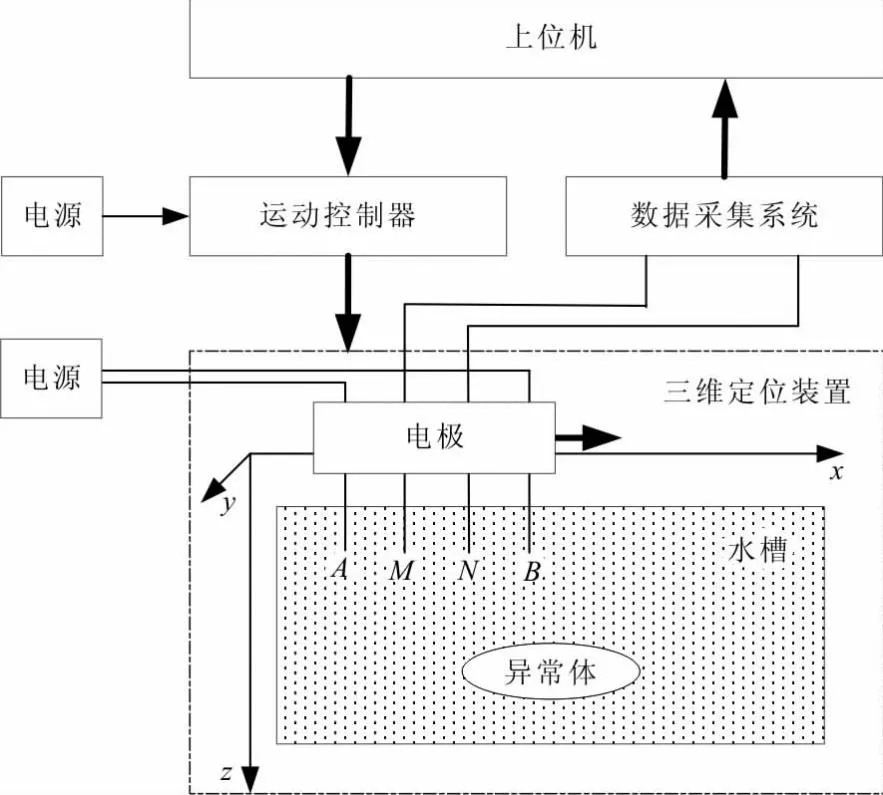
图2 勘探模拟实验平台示意图Fig.2 Schematic diagram of exploration simulation experiment platform

为了更好地验证水域电法勘探效果,搭建了一个物理模拟实验平台如图2所示,用于后续实验的展开。水域电法勘探物理模拟实验平台能够模拟海洋环境下拖曳式直流电法实际勘探情况。实验平台主要由四大部分组成,分别为上位机(LabVIEW编程)、四轴三维运动系统、电源模块和电压采集模块,如图2所示,为模拟勘探平台框架图。实验用长方体水槽规格为2 m(长)×1 m(宽)×0.5 m(高)。为了直观展示测量结果,实验采用对称四极装置对石墨块(约10 cm)进行测量。

为了更加直观地展示去噪效果,利用图2所示平台,获取一组水域直流电测量数据,并进行频谱分析,得到图3的电压曲线,对其进行频谱分析,结果如图4所示。可以发现,直接采集的信号噪点比较多,当电极运动到在石墨块上方时,电压出现下降,但下降幅度为0.6 V,噪声幅度为0.3 V,由于噪声的耦合导致后半段变化不明显,利用式(17)可以求得信号信噪比为25.514 9。分析频谱图可以发现,噪声信号在50 Hz附近有一个较大的峰值,同时100 Hz附近有较小的波峰,是由工频噪声及其谐波导致的。因此如果在实际勘探中直接采集直流电压信号,信号过于微弱,有可能导致异常点淹没在噪声中,因此滤波和去噪是有必要的。

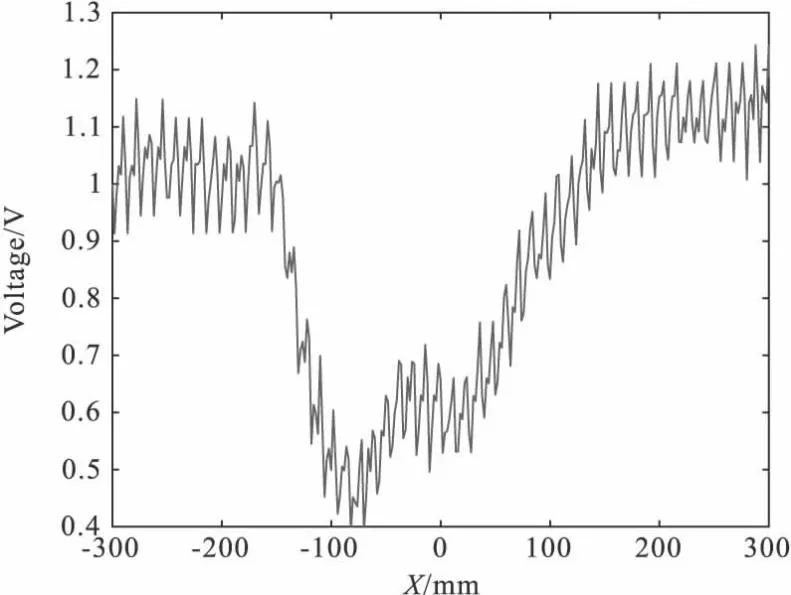
图3 模拟实验直接采集电压信号Fig.3 Direct acquisition of voltage signal in simulation experiment

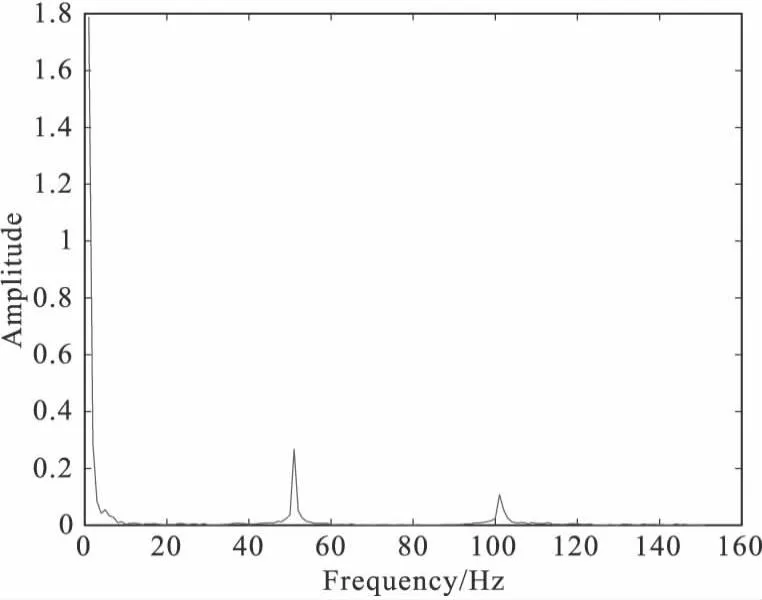
图4 模拟实验直接采集电压信号频谱Fig.4 Spectrum of voltage signal directly acquired in simulation experiment

3.2 高斯窗参数

为了明确不同的高斯窗参数a对谐波滤波器去噪效果的影响,分别选取了a为0.1,0.5和0.8时的谐波滤波器幅频曲线。得到结果如图5。

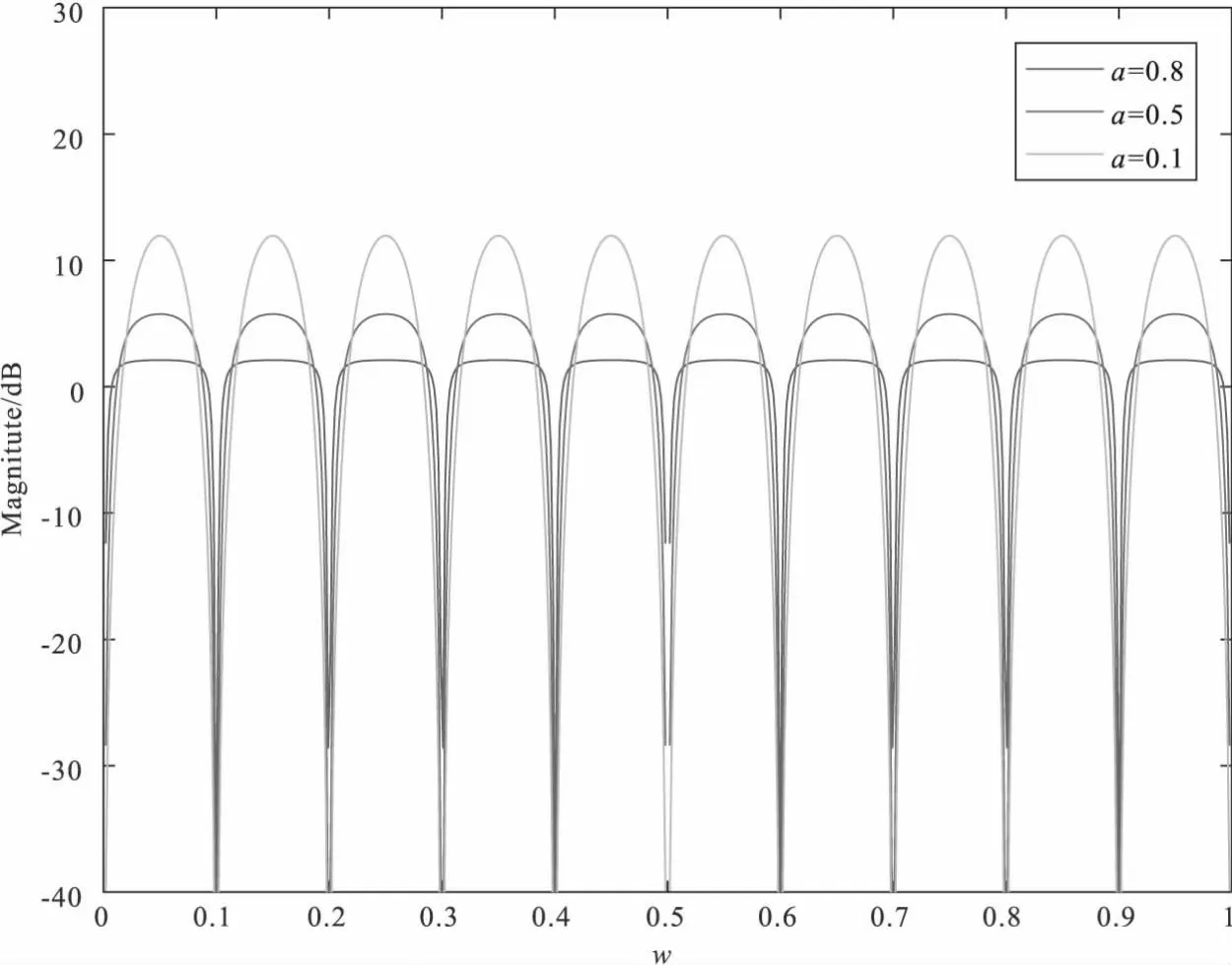
图5 不同a值的去噪效果Fig. 5 Noise removal effect of different a values

通过对比发现,当a增大的时候,谐波滤波器频率响应曲线会变得平坦,对其他频率信号影响较小,但滤波效果会变差,衰减会减小,当a=1时会变成全通滤波器。当a减小的时候,可以发现谐波滤波器的频率响应变得凸出,但是信号在中心频率处衰减迅速,滤波效果较好,同时对其他频率的信号影响较大。因此,对高斯窗参数a的选择为0.5比较合适。对设计好的滤波器进行实际信号的滤波,得到如图6的去噪信号,其频谱如图7所示,对比结果可以发现该滤波器对工频噪声及其谐波有一定的抑制作用。

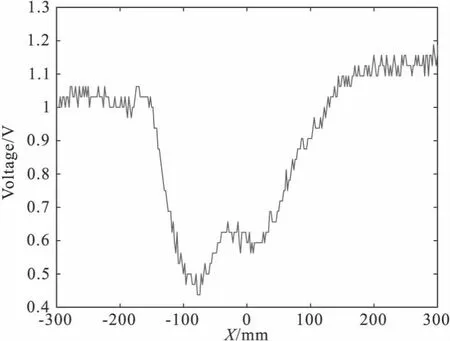
图6 谐波滤波器去噪信号Fig.6 Harmonic filter denoising signal

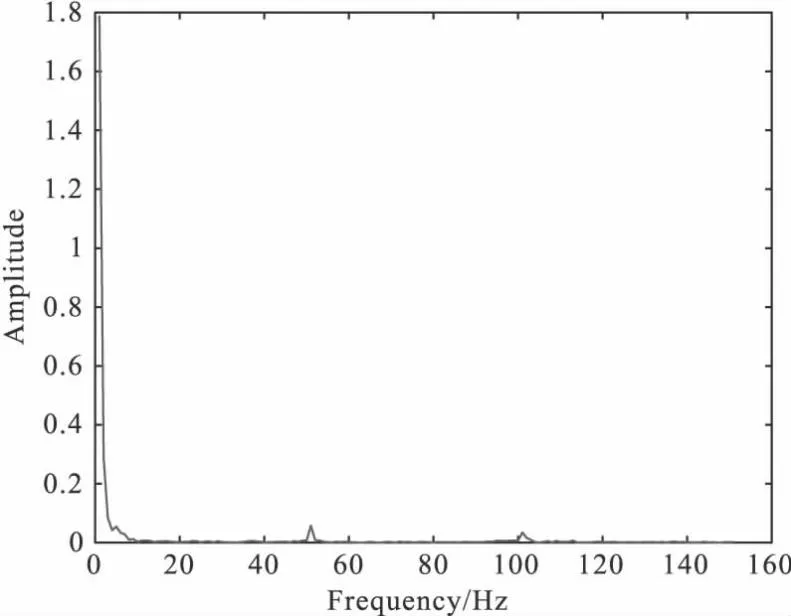
图7 谐波滤波器去噪信号频谱Fig.7 Spectrum of harmonic filter denoising signal

3.3 小波基选取

利用图2所示的测试平台,获取了一组水槽直流电探测数据。将Coiflet小波基、Symlet小波基和Daubechies小波基分别进行噪声处理测试。对比结果(图8),为了更清晰展示细节,将图8红框中进行放大得到图9,结果表明Coiflet小波基的效果是不满意的,无法有效去噪;Daubechies小波基的效果比Coiflet小波基的有所改善,但是仍然存在明显的噪声波动且信号不够平滑;Symlets小波基有较好的效果,噪声波动被明显减少,同时水槽实验中采集的直流电压信号变得平滑。因此,这个结果验证了Symlets小波基是比较适合水域直流电探测。通过计算,相较于直接采集的信号,经过处理后的信号信噪比为33.587 1。

图8 不同小波基去噪效果Fig.8 Effect diagram of noise removal with different wavelet bases

图9 不同小波基去噪效果图局部细节Fig.9 Partial details of different wavelet basis denoising effect

4 探测结果

在水槽中,使用自动跑极装置进行三次测试,电极排列装置为对称四极装置,供电电极AB间隔为10 cm,测量电极MN间隔为2 cm。第一次采集不放置石墨块,用于采集水槽无目标状态下的探测效果;第二次实验将石墨块用绳子吊起来,放置于水槽中间位置;第三次实验将石墨块放置于水槽底部,在不进行任何去噪处理的情况下,得到图10的采集电压数据,此时,三次采集信噪比分别为23.782 7、25.514 9和24.623 1,可以发现:采集电压信号有较大的波动,尤其当探测目标放置在水槽底部时,采集电压较小,采集的信号被噪声淹没,对后续视电阻率的计算存在困难。对其进行谐波滤波器和小波变换去噪后得到结果如图11,可以发现信号变化更加明显,三次采集信噪比提高到了30.365 2、33.587 1和31.745 3,这将有利于视电阻率的计算。

对水槽模拟实验采集的电压数据进行谐波滤波器和小波去噪处理后,利用式(18)计算视电阻率:

(18)

图11 去噪处理的探测数据Fig.11 Detected data after de-noise processing

最后得到结果如图12所示,通过对比实验分析得到:由于水槽使用淡水,在无目标的情况下测得水的电阻率为21.8 Ω·m,符合理论实际。对比石墨块放置于半水深和水底测得的视电阻率,可以发现当电极阵列支架越靠近测量被测石墨块时,视电阻率变化越大,勘探效果越好。

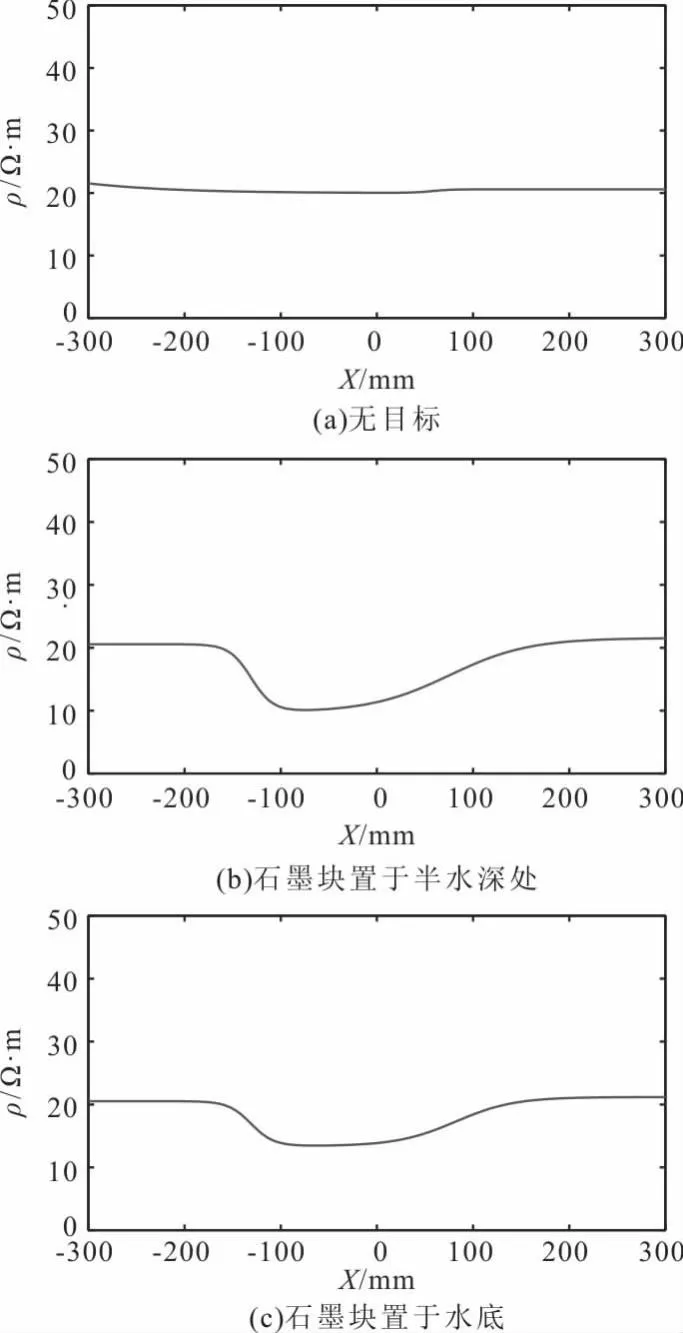
图12 勘探实验视电阻率计算结果Fig.12 Calculation results of apparent resistivity of exploration experiment

5 结论

针对目前水域电法勘探存在工频噪声及其谐波干扰导致采集数据精度不高的问题,提出了一种基于谐波滤波器和小波去噪的方法来对采样数据进行去噪处理,结合水域电法原理进行视电阻率计算。首先确定了谐波滤波器中高斯窗因子a的取值为0.5时以及小波去噪中小波基采用Symlets小波基时,有较好的去噪效果。而后基于搭建的实验平台进行数据采集,对水槽模拟实验采集电压数据中的工频噪声及其谐波进行抑制,使用小波方法对采集的电压信号再次去噪,在水槽模拟实验中,对于异常最大的采集信号的信噪比从25.514 9提高到了33.587 1,而无异常情况下信噪比从23.782 7提高到了30.365 2。最后,计算得到无目标时,水底视电阻率计算结果为21.8 Ω·m,放置石墨块时,上方的水下视电阻率降为10.1 Ω·m,符合预期结果,验证了该去噪方法的可行性,具有深入研究的价值。