基于加权弹性网络回归的个性化HRTF方法研究
冯莹依,刘海生
(同济大学声学研究所,上海 200092)
0 引言
在过去的几十年中,用于模拟空间声源的音频信号处理技术受到越来越多的关注,并在实际生活中得到应用,如沉浸式虚拟环境[1-2]、虚拟乐器[3]、AR 耳机[4]等。其中,基于头相关传输函数(Head Related Transfer Function,HRTF)的声信号处理技术是虚拟听觉技术的重要组成部分。HRTF指人耳鼓膜处接收到的声压与同一声源在头移开后在头中心产生的声压之比[5],在自由场条件下,声源的空间位置信息可以通过这样一对左右滤波器处理得到。所以HRTF对于空间声重放有着重要意义。
HRTF反映了声音信号从声源传递到听者耳膜的路径中的所有线性变化,包含了人体躯干、头部以及耳廓等的反射和衍射效应[5]。然而每个人的生理参数都不相同,即HRTF 是个性化的。研究发现,在实际应用中使用非个性化的HRTF会导致声像前后反转[6]、仰角误认[7]以及头中定位[8]等情况。因此,使用个性化的HRTF 才能获得更佳的听觉效果。
当前对个性化HRTF的获得方式主要有实际测量、仿真计算以及近似估计等[9]。实际测量是获取HRTF最直接的方法,但对于设备与人员操作的要求都较高,且过程复杂繁琐,所以对每一位受试者进行实测是不现实的。同样仿真计算对计算设备的要求也比较高。为了便于HRTF的相关研究,许多实验室公开了测量结果,一些通用数据库中还包含了受试者的生理参数数据,如被使用较多的来自美国加州大学戴维斯分校图像处理和集成计算中心(CIPIC)的数据库[10]等。
考虑到HRTF与生理参数的相关性,基于生理参数的近似估计获取HRTF的相关研究在近些年广泛展开。Zotkin等[11]提出假设:如果受试者之间的生理参数相同,那么其对应的HRTF 也应该相同。他们通过匹配新受试者的生理参数与数据库中所有样本生理参数之间差值最小的样本作为新受试者的HRTF,不过在这种方法中仅使用了7个生理参数,且在数据库匹配过程中略显粗糙。近年来Zotkin课题组仍在为如何实现快速便捷地获取个性化HRTF做出相关工作,2022年研究了通过2D耳朵照片与头部尺寸计算误差来匹配到数据库中的耳朵,以实现HRTF个性化匹配结果[12]。Lu等[13]使用稀疏主成分分析和稀疏表示的匹配算法获取数据库中与受试者具有相同稀疏系数的HRTF数据,并通过两个数据库客观验证了方法的有效性。但即使是最接近的匹配并不能保证在所有情况下都有很好的效果,因为这种方法只是返回数据库中最接近的非个性化HRTF,而且并不允许受试者对HRTF 进行相应的调整。此外,一些研究通过将生理参数与HRTF建立映射关系,从而通过新样本的生理参数得到新的HRTF。如使用神经网络的算法,Chen等[14]使用基于生理参数的深度神经网络自动编码获得HRTF,Lu 等[15]提出一种基于生理参数和声源方向重构HRTF的深度神经网络模型。但使用这类方法对样本数据数量的要求比较大,较少的样本实验数据可能会导致过拟合的情况从而产生误差。
有研究者试图不直接建立生理参数与HRTF之间的映射关系,简化新样本HRTF的获取过程。Bi‐linski等[16]假设HRTF可以通过生理参数的稀疏表示得到,即将新样本的生理参数用数据库中的生理参数进行稀疏表示得到稀疏系数,继而与数据库的HRTF 合成来得到新样本的HRTF 幅度,结果也验证了这种方法的有效性。后续的研究对数据的预处理和后处理方式进行了改进与比较,进一步提高了方法的性能[17-18]。然而在进行稀疏表示时,以上方法都使用的是仅含有L1范数的套索回归算法(Least Absolute Shrinkage and Selection Operator,LASSO)。L1 范数可以产生稀疏性,但仅保留贡献较大的参数,往往会忽视一些信息,使得回归结果不能全面地反映参数的贡献。Zou等在21世纪初提出了弹性网络(Elastic Net,EN)算法[19],他们表示若在LASSO回归的基础之上引入L2范数,在L1范数保证结果的稀疏性同时,L2 范数保证筛选参数的全面性,可以达到更理想的效果。
相较于认为所有生理参数对HRTF贡献相同的算法,考虑生理参数与HRTF幅度的相关性而对不同的生理参数进行加权更能反映参数值的贡献,从而可以提高估计值的准确性。在此基础上结合EN回归算法的优越性,本文提出了一种基于加权弹性网络回归的个性化HRTF方法。本文首先将对公开数据库中样本的生理参数与对应的HRTF幅度进行相关性计算,获取不同参数的权重对其进行加权,然后使用加权弹性网络回归计算新样本与数据库中样本生理参数的稀疏系数,最后将得到的稀疏系数与数据库样本的HRTF集结合就可以得到新样本的HRTF幅值。使用这种算法,只需要获得受试者的生理参数,就可以简单有效地获取个性化HRTF的估计值。
1 HRTF个性化算法
1.1 HRTF数据库
本文中使用的数据库是CIPIC数据库,其中包括了45位受试者在1 250个方向上的数据,以时域即头相关脉冲响应(Head Related Impulse Response,HRIR)的形式存储。同时该数据库提供了对应的27项生理参数,但只有35组数据具有所有的27项生理参数记录值。本文研究将使用这些完整的数据展开。同时为了验证算法的有效性,将选择其中的32组数据为数据集,其余3组为检验样本。
1.2 HRTF预处理
在自由场条件下,HRTF的定义式可以表示为
其中:HL、HR分别表示左右耳的HRTF,PL、PR分别表示左右耳接收到的声压,P0表示同一声源在头移开后在头中心位置产生的声压,r表示声源到听者的距离,θ表示声源的方位角,φ表示声源的仰角,f表示频率,a表示听者的头部半径。
因为在CIPIC数据库中数据是以时域的形式存储的,所以首先对数据库中的HRIR 数据进行256点的快速傅里叶变换使之转换为频域上的HRTF,然后再对HRTF进行取幅度的处理,本文将对幅度进行个性化合成:
其中:Horiginal表示原始数据库中的HRTF 集,H表示处理后的HRTF幅度矩阵,大小为129×32。
1.3 人体测量参数选择
目前研究对生理参数的选择并没有一个统一的标准,且不同研究中采用的筛选方式不同导致最后筛选出的结果也不相同。由于CIPIC数据库中的几项生理参数测量不便,本文考虑到生理参数获取的便利性,参考文献[20]中的方法,选择用3 张平面图就可以读出的19项生理参数,如图1所示。

图1 生理参数示意图[20]Fig.1 Schematic diagram of anthropometric features[20]
1.4 权重计算
已有研究发现,不同的生理参数对HRTF的贡献并不相同[17-18]。本文通过计算相关性来对不同的生理参数进行加权。结合已有文献中的方法,首先将数据库中的P位受试者样本的B项生理参数数据构成一个二维数组AB×P,即:
其中:Ab,p表示第p个受试者样本的第b项生理参数。然后再对生理参数进行标准化:
本文通过成对比较来评估不同生理参数对HRTF的贡献。首先计算B项生理参数的2B-1种生理参数组合下,两受试者之间生理参数的距离与相应两受试者谱偏差(Spectral Deviation,SD)的相关性,即:
其中:wb为第b个生理参数对应的权值,tb表示第b个生理参数在相关性最大的生理参数组合中出现的次数。由式(8)计算在本文中得到的权值,结果如表1所示。

表1 各生理参数对应的权值表Table 1 the weights corresponding to anthropometric features
1.5 加权弹性网络回归
结合1范数和2范数共同作用的优越性,以及上文中对不同生理参数根据相关性赋予不同的权值,本文提出加权弹性网络回归来获得新样本的生理参数稀疏表示,表达式为
其中:α=[α1α2…αP]T表示新样本生理参数在数据库中样本集生理参数的稀疏系数,w=[w1w2…wB]是由上部分计算出的权值组成的数组,A0表示新样本的生理参数,A表示数据库样本集对应的生理参数集,λ1和λ2表示正则化参数。为了便于后续的计算,对式(9)进行整理,令:
其中:β∊[0,1]。将式(10)代入式(9)得到整理后的基于加权弹性网络回归对生理参数进行稀疏表示的表达式:
1.6 贝叶斯优化
因为式(11)中存在两个未知参数,且理论上β与λ有无数种组合方式,而参数的选择也会影响最终效果。因此需要一种简单有效的方式找到最优解。本文选择使用贝叶斯优化来实现参数的选择。
贝叶斯优化是一种全局优化算法,能够更加有效地找到全局最优解。因为贝叶斯优化过程是寻找实现最大化采集函数的参数β与λ,所以本文以估计值与真实值的偏离程度作为评判指标,即选择谱偏差的倒数作为指标函数,第d个声源方向上的谱偏差RSD(θd,φd)的表达式为
在强化思想教育的同时,也要加强对党员干部特别是领导干部的严格管理。一方面,严格考核干部。明确干部考核指标,提升干部考核的针对性,推进述职评议考核,落实督查、问责、约谈机制,督促干部落实责任,推进考核评价结果与干部晋升薪酬等挂钩。另一方面,严格监督干部。加强对班子换届、干部调整、机构改革、婚丧嫁娶、新居乔迁、子女考学等重点时段的监督检查,健全“为官不为”的教育惩戒机制与容错纠错机制。
令:γ=γ(λ,β),于是指标函数y(γ)可以表示为
参考文献[21]所述,本文选择高斯过程和上置信边界作为概率先验模型与采集函数,这样的配置具有高灵活性和可扩展性,也利于整个优化过程的进行。首先构造一个高斯过程:
其中:e为均值函数,k为核函数。为方便起见,本文中取e=0,k选择平方指数协方差函数。对于每一组Γ=[γ1γ2…γz]T都满足一个联合高斯分布N(0,K),K为协方差矩阵,即:
假设有一组一致的样本点{Γ,Y},Y=[y1y2…yz]T,对一组新样本yz+1,有:
其中:K'=[kz+1,1kz+1,2…kz+1,z]。可算出yz+1的后验概率:
最后设置上置信边界函数,表达式为
1.7 HRTF合成
结合上述,我们就可以通过获得的稀疏系数来合成新样本的HRTF幅值,即
其中:α=[α1α2…αP]T是由式(11)计算出的稀疏系数,H为式(2)处理得到的数据库样本的HRTF幅值,H′表示通过本文算法得到的新样本HRTF对数幅值的估计值结果。最后将对数幅度转换回初始单位即可得到最终结果:
其中:Hnew表示通过新样本生理参数计算得到的HRTF幅度估计值。
图2给出了个性化HRFF算法的流程图。

图2 个性化HRTF算法流程图Fig.2 Block diagram of the personalized HRTF method
2 算法测试与结果分析
本章将展示本文提出算法的有效性。首先取测试样本1的生理参数代入算法,通过贝叶斯调参获得加权弹性网络回归的最优参数组合(0.02,0.5)。测试样本1合成结果与实测曲线对比图如图3所示。图3 中展示的是分别在竖直方向上平移了70 dB 和140 dB的结果,位置点使用的是CIPIC的坐标系规定,括号中的角度数据前者表示方位角大小,后者表示仰角大小。由于篇幅有限选择了三个位置,分别是水平面同侧耳方向、水平面异侧耳方向以及一个中垂面仰角方向,可以看到估计值与实测值比较接近,曲线走向基本一致。同时相较于低频段,估计值在高频段误差较大。同样的方法我们可以获得其余测试样本的合成结果。

图3 测试样本1合成结果与实测曲线对比图Fig.3 Curve comparison between the synthetic results and the measured results of test sample 1
得到三个测试样本的HRTF幅度估计值后,为了进一步展示不同频段的合成效果,根据式(12)和式(13)计算估计值与测量值在不同频段不同位置点的谱偏差来进行比较。为说明在低频段、不同的峰谷频段以及全频段的合成效果,这里分别计算了每一个测试样本在0~8 kHz、4~10 kHz、10~16 kHz以及0~22.5 kHz 的平均谱偏差结果,如表2所示。可以看到0~8 kHz的谱偏差相较于其他频段是比较小的,而在10~16 kHz频段的谱偏差甚至要高于全频段,说明该算法对于低频段的合成效果是较好的,但对峰谷频段的合成上有待进一步的提高。

表2 测试样本在不同频段下的平均谱偏差Table 2 Average spectral deviations of test samples in different frequency bands
Nishino 等[22]经过实验验证后得出结论:在小于8 kHz 的频率范围内,HRTF 估计值的谱偏差小于4.0 dB就可以有足够的声音定位效果。对不同声源位置点在小于8 kHz频率范围与全频带范围内的谱偏差结果比较,结果如图4所示。这里的位置点指的是数据库HRTF 测量的共1 250 个位置点。从图4中可以直观看到不同位置点的合成效果是不同的,且相较于与耳同侧声源位置,异侧声源的谱偏差明显更高,这可能是因为声源到达同侧耳要比到达异侧耳的接收点过程中受到的反射、散射等较少,使得频谱曲线较平滑,细节较少,使用算法获得的估计值结果能更接近实际值,从而使得相比之下的谱偏差更小。同时从图4可以比较明显地看出相较于全频带,合成结果的准确度在小于8 kHz的频带内较好,且在大多数位置点满足谱偏差小于4.0 dB,这也进一步说明了本文方法的有效性。
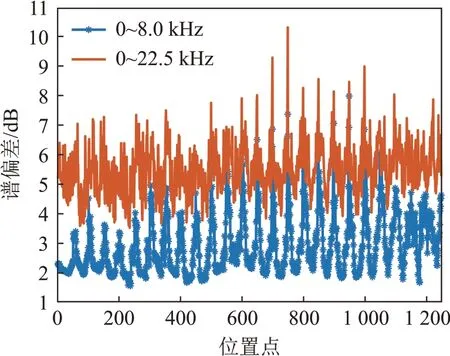
图4 在不同带宽范围内的平均谱偏差对比图Fig.4 Comparison of average spectral deviations in different bands
因为所用到的数据库样本数量有限,本文在此基础上对数据使用留一法(Leave One Out,LOO)进行交叉验证,计算了每一个样本作为测试集的平均谱偏差结果,绘制了曲线图,结果如图5所示。可以明显看出所有的谱偏差结果都约为一定值,通过计算获得所有值的平均值为5.42 dB,与测试集得出的结果相近,证明了本文算法的有效性与结果的可靠性。
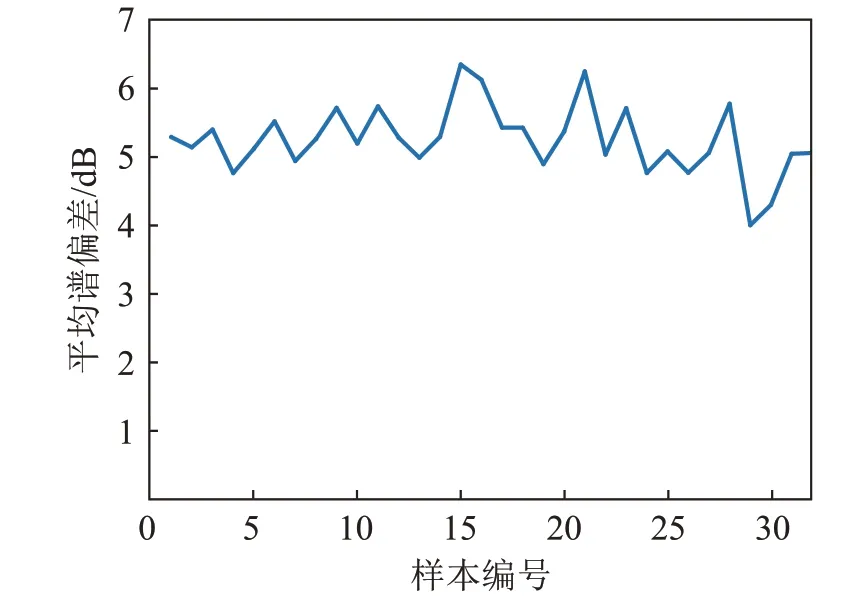
图5 本文算法的平均谱偏差交叉验证结果Fig.5 The result of the average spectral deviation obtained by cross-validation of the method proposed in this paper
为了进一步展示本文算法的有效性,将与文献[16]和文献[18]中使用的LASSO 回归以及加权LASSO 回归方法进行对比。观察数据库中的生理参数可以发现,左右耳的生理参数并不是完全对称的,于是在计算中同时考虑了这一特殊性,即分别计算了左右耳的谱偏差结果以及平均谱偏差进行对比,结果如表3所示。观察表3中的数据可以看到,无论是左右耳结果还是平均结果,本文算法的平均谱偏差结果都小于另外两种算法的结果。同时可以发现,左右耳的结果并不是完全相同的,且有的方法实现的左右耳结果会存在较大的不同。考虑到左右耳的差异,在后续的相关研究中有必要使用左右耳不同的数据来分别进行合成计算。
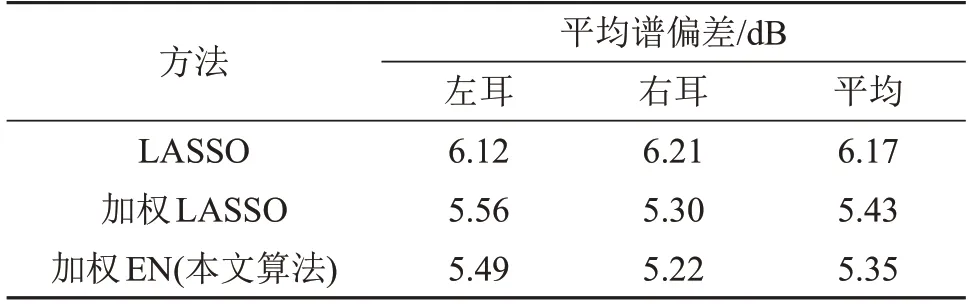
表3 三种方法下的平均谱偏差Table 3 Average spectral deviations under three methods
结合平均谱偏差结果,图6是不同算法下测试样本在不同位置点的左耳平均谱偏差结果。通过前两种算法比较可以看出,对生理参数进行加权可以提高估计值的准确性,说明在使用生理参数来估计HRTF幅度中,考虑不同参数的不同贡献值进行计算是有必要的。比较文献算法与本文算法,本文的EN 算法在L1 范数的基础上引入L2 范数来进行回归计算提取稀疏系数,L1 范数保证结果的稀疏性同时,L2 范数保证筛选参数的全面性,能进一步提高估计值的准确度,这一点从结果数据中也得到了证明。
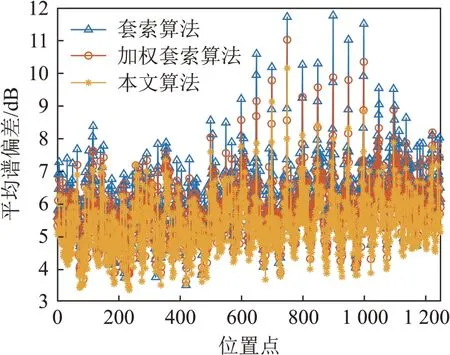
图6 使用三种方法在不同位置点上的平谱偏差对比图Fig.6 Comparison of the average spectral deviations at different locations with three methods
3 结论
本文在已有用稀疏表示获取个性化HRTF方法的基础上,提出一种基于加权弹性网络回归的个性化HRTF算法。该算法只需获得新样本的生理参数即可合成个性化HRTF幅度,使用加权弹性网络回归的方法进一步减小了估计值与真实值之间的谱偏差,提高了估计值的准确性。本文方法使用的生理参数可以直接从三张平面图读取出来,简化了生理参数的获取过程。研究结果表明,该方法有较好的合成效果,尤其在中低频段的谱偏差较小,进一步提高了使用稀疏表示合成个性化HRTF 幅度的准确度。
虽然本文方法相较于之前的稀疏表示合成HRTF的方法准确度有所提高,但最终得到的结果仍然存在一定误差,部分位置点的谱偏差较大,所以对于单个点的合成准确度还有待进一步提高。除此之外,从估计值与真实值的对比来看,该算法在不同频段出现的误差不同,后续可以考虑对低频、中频和高频用不同的预测模型以及精度要求展开研究。最后,本文是获取HRTF幅度估计值的一个计算过程,仅做了客观验证的工作,未来的工作可以对相位进行获取并使用感知定位测试的方法来验证HRTF估计值的主观有效性。

