硅酸镓镧晶体谐振器的高频振动分析

吴荣兴，王晓明，唐忠平，王骥

(1.宁波职业技术学院应用力学研究所，浙江宁波 315800；2.宁波大学机械与力学学院，浙江宁波 315211)

0 引言

石英晶体谐振器因其频率高、稳定性好、抗干扰性强等特性，在通信工程、航空航天、传感检测等领域都得到了广泛的应用[1-2]。针对石英晶体谐振器的高频振动，Mindlin 通过将位移和电势展开为厚度坐标幂级数的方式将三维弹性问题转化为二维问题，分析了石英晶体谐振器的振动特性和电学参数[3]。Lee等[4]和Peach[5]分别提出了基于三角函数展开和特征值的板理论，同样可以用于石英晶体板高频振动的特性分析。Yang等[6]对于石英晶体谐振器的结构参数变化和偏场方法及其应用进行了大量的研究。Patel等[7]通过有限元方法分析了非线性效应对石英晶体谐振器振动特性的影响，初步解释了激励电平效应。文献[8-11]建立了考虑材料和几何非线性的石英晶体板高频振动方程，并利用解析方法和数值方法对非线性方程组进行了求解，获得了不同驱动电压下的频率响应曲线。

随着电子行业对谐振器微型化和高频化需求的不断增加，各类新材料压电声波谐振器的研究得到了广泛的开展。其中硅酸镓镧(La3Ga5SiO14,LGS)是一种性能优异的新型压电晶体材料，相比于石英晶体材料，硅酸镓镧具有更强的压电系数、更高的阻抗、更大的介电常数和机电耦合系数[12-15]。硅酸镓镧晶体材料开始应用于各类传感器、谐振器、滤波器等电子器件的试制[16-17]。目前的硅酸镓镧晶体谐振器的试制过程都是依据经验选取一定尺寸范围的晶片进行制作，经测试其振动特性和电学参数后再细化所选定的晶片尺寸，费时费力且结果不尽如人意，需从振动理论上对硅酸镓镧晶体谐振器设计提供指导。开展新材料硅酸镓镧压电声波谐振器振动理论及设计方法研究，将会促进压电声波理论的进一步完善和求解方法的创新。

本文利用Mindlin 一阶板理论分析了硅酸镓镧晶体板强耦合的厚度剪切振动和弯曲振动，获得了硅酸镓镧晶体板高频振动的色散关系、频谱关系和振动模态位移图。研究结果为硅酸镓镧晶体谐振器的设计提供了指导。

1 基本方程

硅酸镓镧是一种具有独特优点的多功能晶体材料，在压电声波谐振器和滤波器中已经得到了不断的应用[13]。硅酸镓镧谐振器的设计首先要解决的问题就是确定晶片的尺寸，也就是晶片的长度、厚度和宽度。硅酸镓镧晶片的厚度由工作频率初步确定，接着确定晶片的长度，也就是设计最佳的晶片长度，从而确保谐振器工作特性的稳定，宽度对谐振器振动特性的影响不大[1-3]。需要设计的硅酸镓镧晶体板如图1所示，其长度、宽度和厚度的尺寸分别为2a、2c和2b。

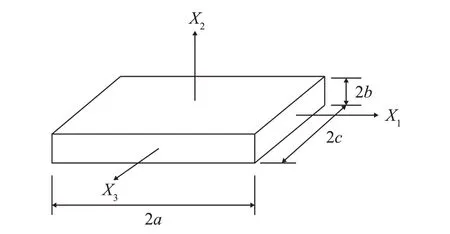
图1 硅酸镓镧晶体板示意图Fig.1 Schematic diagram of a La3Ga5SiO14 crystal plate

基于Mindlin 板理论的位移假设，将位移展开为厚度坐标x2的幂级数[3]

硅酸镓镧晶体板的运动方程为[3]

式中：Tij和b分别为应力表达式和硅酸镓镧晶体板的半板厚。

高阶本构关系为

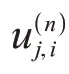
2 色散关系

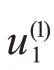
对高阶位移进行截断和选取后，可以得到应力位移的表达式：

基于直峰波位移假设，可以令位移为[18-19]

式中：A1(A2)、ζ和ω分别为振幅、波数和频率。

为了计算简单，可以将频率、波数和波速进行归一化处理：

将位移表达式(8)代入应力表达式(7)，最终代入式(6)中的运动方程，可以得到：

由于振幅A1(A2)有非零解，因此要求式(10)的系数矩阵行列式的值为0，即：

式(11)即为硅酸镓镧晶体板高频振动的色散关系。确定硅酸镓镧晶体材料的弹性常数后[13]，利用Matlab软件编程计算获得了硅酸镓镧晶体板高频振动的色散关系，即频率和波数的关系，如图2所示。主要计算思路是在式(11)中设定一个归一化频率值，通过Matlab软件中的Solve函数求出归一化波数解，然后绘制硅酸镓镧晶体板高频振动的色散关系图。

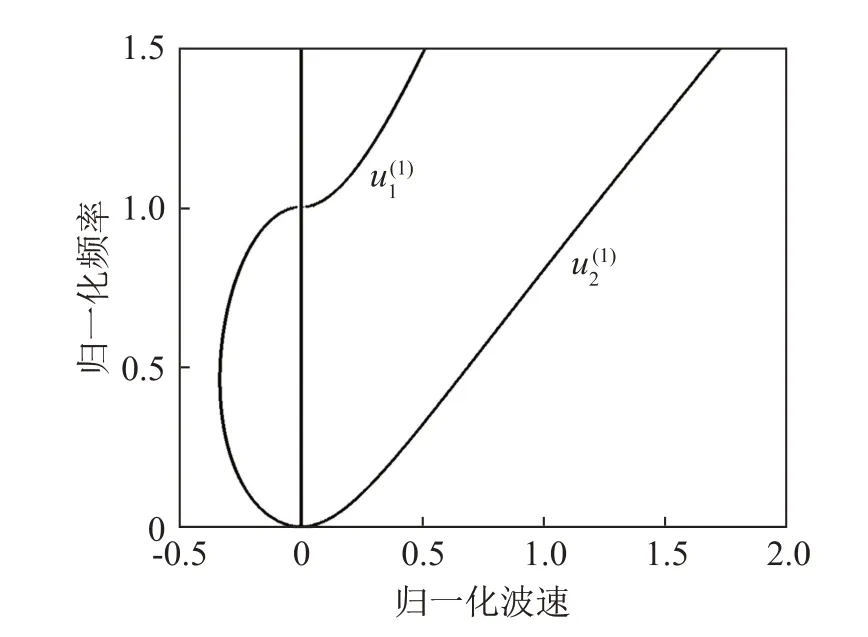
图2 硅酸镓镧晶体板两种振动模态的色散关系Fig.2 Dispersion curves of two vibration modes of the La3Ga5SiO14 crystal plate

从图2可以发现硅酸镓镧晶体板的厚度剪切振动模态的一阶截止频率为1，非常精确。这里获得硅酸镓镧晶体板的色散关系与石英晶体板的色散关系类似。石英晶体板厚度剪切振动时如未考虑修正，获得的一阶截止频率为0.97，为此Wang 等提出了自然修正法和对称修正法来保证一阶截止频率为1[1-3]。

3 频谱关系

通过色散关系式(11)可以得到两个波数解，位移的表达式可表示为

式中：A21/A22、α1/α2和Z1/Z2分别为新定义振幅、振幅比和两个波数。振幅比的定义为

同样将位移表达式(12)代入应力表示表达式(7)，可以得到：

对于如图1所示硅酸镓镧晶体板，在长度方向的边界条件为

式中：a为硅酸镓镧晶体板板长的一半。

将式(14)中的应力表达代入式(15)中的边界条件，可以得到关于振幅A21(A22)的两个方程组。同样振幅A21(A22)有非零解，令其系数矩阵的行列式值为0，即：

给定硅酸镓镧晶体的尺寸后，可以获得硅酸镓镧晶体板高频振动的频谱关系，也就是频率和长厚比关系如图3所示。频率关系的计算思路为设定硅酸镓镧晶体板的一个长厚比，利用Matlab软件中的二分法程序对式(16)中的行列式方程进行求解，获得其归一化频率。

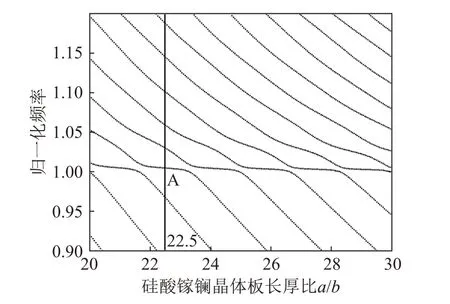
图3 硅酸镓镧晶体板归一化振动频率与长厚比(a/b)关系图Fig.3 Relationships between normalized vibrations frequency and a/b of the La3Ga5SiO14 crystal plate

选定硅酸镓镧晶片任意一个长厚比，可以获得多个频率解，每个频率解表示一种振动形式，可以绘制每个频率解的振动模态位移图，比较各振动模态位移的大小来确定其主振模态[1-3]。研究表明斜率较大的斜直线部分为弯曲振动模态，此时弯曲振动是主振模态；而在归一化频率1附近的平坦部分为厚度剪切振动模态，此时厚度剪切振动是主振模态[18-19]。

图3表明在硅酸镓镧晶体板高频振动时，弯曲振动模态u(0)2和厚度剪切振动模态u(1)1存在强耦合，随着频率和长厚比的变化，两种模态也在不停地相互转换[3]。在石英晶体谐振器的高频振动分析过程中，Wang 等提出了选取石英晶板的最佳长厚比来避免弯曲振动模态u(0)2和厚度剪切振动模态u(1)1的强耦合，也就是选取一定的a/b作为晶片的尺寸[18-19]。主要选取思路是选取归一化频率1附近平坦阶段的中间部分、与其他模态存在一定距离的点。依据这一思路，本文同样选取归一化频率随长厚比变化较为平坦中间部分、与其他模态存在一定距离的硅酸镓镧晶片长厚比，也就是如图3所示的A点，其长厚比为22.5。同样可以选取同样的点作为硅酸镓镧晶体板的最佳尺寸，也是谐振器设计和制造企业急需确定的晶片尺寸。

可以进一步重写位移表达式：

式中：β为振幅比，其定义为

基于式(17)中的位移表达，在提取振幅A22后，可以绘制出硅酸镓镧晶体板各振动模态的位移如图4所示。

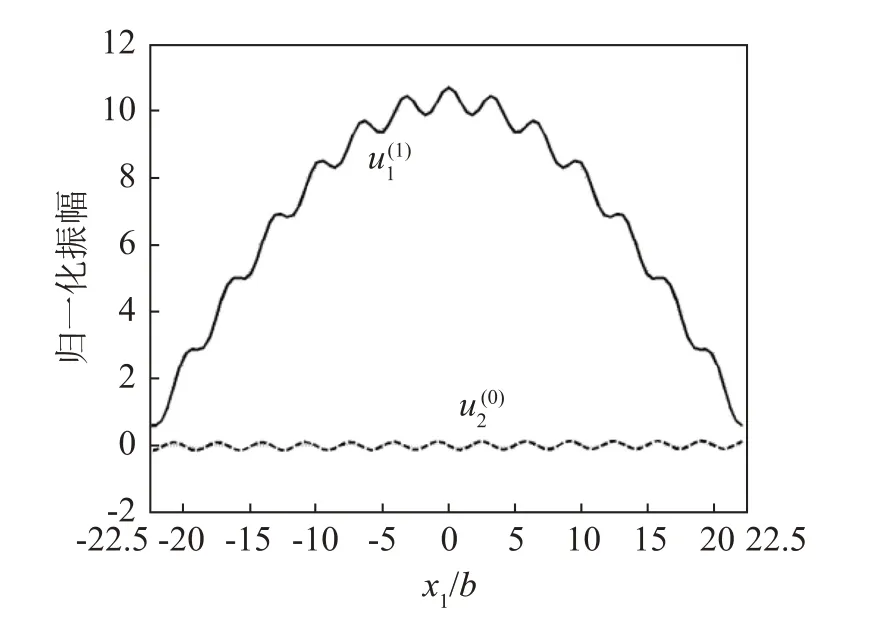
图4 硅酸镓镧晶体板的两种振动模态的归一化位移与x1/b 关系图Fig.4 Relationships between normalized displacements of two vibration modes and x1/b of the La3Ga5SiO14 crystal plate

从图4中可以发现，在选取硅酸镓镧晶体板最佳长厚比22.5 后，厚度剪切振动模态u(1)1是硅酸镓镧晶体板的主振模态，弯曲振动模态u(0)2的振幅相对于厚度剪切振动模态u(1)1的振幅较小，表明两种模态不存在强烈耦合，此时的尺寸可以作为硅酸镓镧晶体谐振器的设计尺寸。同时图4表明厚度剪切振动模态u(1)1的位移主要集中在硅酸镓镧晶体板的中间，具有很好的能陷效应[8-10]。综合利用硅酸镓镧晶体板的频谱关系和振动模态位移关系可以指导硅酸镓镧晶体谐振器的设计，避免了试凑硅酸镓镧晶片尺寸的复杂过程[1-2]。

4 结论

基于Mindlin 一阶板理论，本文分析了硅酸镓镧晶体板的厚度剪切振动和弯曲振动，获得了硅酸镓镧晶体板的色散关系、频谱关系和振动模态位移图。获得的色散关系表明Mindlin 板理论同样可以应用于硅酸镓镧晶体板的厚度剪切振动分析，其一阶截止频率非常精确。选取硅酸镓镧晶体板高频振动的频谱关系中基频附近较为平缓的点作为最佳尺寸，绘制该尺寸的振动模态位移图，结果表明厚度剪切振动模态是硅酸镓镧晶体板的主振模态，与弯曲振动模态的耦合较弱且能陷效应较为理想。本文建立的方程和获得的结果可以用于指导硅酸镓镧晶体谐振器的实际研发。