基于鲁棒主成分分析和MFCC反复结构的歌声分离方法
熊天,张天骐,闻斌,吴超
(重庆邮电大学通信与信息工程学院,重庆 400065)
0 引言
音乐是表达人们内心情感的一种方式,不同类型的音乐表达了不同的情感。在实际应用中有很多场景需要用到这些信息,例如歌手识别、音乐信息检索和歌词识别。但是,当背景伴奏存在时,会对歌声的识别与分析产生干扰。所以分离歌声与背景伴奏是很有必要的。
人类听觉系统在从背景伴奏中分离出歌声方面具有很强的能力。虽然这对于人类来说毫不费力,但是对于机器来说却很困难。面对困难,很多学者也提出了诸多歌声伴奏分离的方法。Erdogan等[1]将谱掩码非负矩阵分解(Non-negative Matrix Factoriza‐tion,NMF)方法应用到了歌声分离领域并且取得了不错的分离效果。文献[2-3]中提出将概率窗与非负矩阵分解结合的一种算法。但是NMF 是一种有监督算法并且非常依赖处理样本和缺乏泛化性。张天等[4]也将二维傅里叶变换(two Dimension Fourier Transform,2DFT)应用到音乐分离任务中,主要是利用2DFT得到音乐的声谱图,利用图像的滤波来确定周期性峰值的位置,最后使用矩形窗来构建掩蔽进行分离。Nerkar等[5]将经验小波变换应用到了音乐分离中,该方法利用经验小波变换对信号进行有效分解,然后寻找信号的重复背景来区分声乐部分和非声乐部分。音乐包含了节奏这一重要的元素,而重复就是节奏的一个重要的特征,基于此,Raffi 等[6]提出了一种重复模式提取技术(Repeating Pattern Extraction Technique,REPET),通过自相关矩阵提取节奏谱[7],进而得到背景音乐的重复周期,以此来建立背景音乐的反复结构来进行音乐分离,但是节奏谱对曲调依赖性较高,而且得到的反复周期是固定的,缺少泛化性。针对REPET 的问题,张天骐等[8]提出了多反复结构模型的音乐分离算法,该算法不再是利用传统的节奏谱来确定反复结构,而是利用整体的梅尔频率倒谱系数(Mel Fre‐quency Cepstrum Coefficients,MFCC)相似矩阵[9]来获取反复信息,提升了模型的泛化性,但是它存在着歌声在低频部分分离不完全的缺点。Huang等[10]从一个假设出发,即音乐伴奏等级低、变化少,而歌声更加稀疏,提出了鲁棒主成分分析(Robust Principal Component Analysis,RPCA)算法对单通道音乐进行分离,将混合音乐分解成为低秩矩阵(背景音乐部分)稀疏矩阵(歌声部分),但是分离出的歌声中往往伴有着低鼓等打击乐器声源,歌声分离不完全。
随着深度学习的发展,越来越多学者将神经网络运用到语音分离的任务中,目前市场上的音乐分离软件(如:SpleeterGui、SongDonkey 以及Audio Jam等)都是基于深度学习框架开发的。由于卷积神经网络(Convolution Neural Network,CNN)在参数量和计算资源消耗方面都要比传统神经网络如:深度神经网络(Deep Neural Network,DNN)和循环神经网络(Recurrent Neural Network,RNN)等都要小,所以目前歌声分离领域大部分都是基于CNN 架构来进行的。Naoya等[11]提出了一种D3NET进行音乐源分离并且取得了在频域分离领域较为先进的性能。文献[12]还将高分辨率网络来进行歌声分离。Bhat‐tarai等[13]提出了一种平行沙漏网络结构来进行歌声分离,该方法将混合音乐幅度谱按频率维度分离3部分:上半部分幅度谱、下半部分幅度谱和全频带幅度谱。Zhang等[14]基提出了一种复杂域中的多任务音频源分离模型,它利用语音、音乐和噪声三种音频信号的频谱特性差异将它们从单通道混合信号中分离出来。文献[15-17]还提出了一系列端到端的网络,这使得在分离任务中不仅考虑了幅度特性,而且还考虑到了相位特性,使分离变得更加全面。2021年,Facebook人工智能研究所[18]在之前研究的DEMUCS[12]架构的基础上又提出了一种时域与频域混合的音乐源分离模型,取得了超过频域模型D3NET 的分离性能,是目前性能最优的模型。虽然深度学习方法普遍比传统方法分离效果好,但是由于深度学习是需要大量数据集来进行训练和测试,需要耗费大量时间,而传统方法没有此过程,耗费时间更少。
上述RPCA方法可以将混合音乐信号分解为稀疏矩阵(歌声部分)和低秩矩阵(伴奏部分),但是如果伴奏中含有打击乐如低鼓、架子鼓等时,由于这些乐器在时域上也表现出和歌声一样的稀疏性,这样就会将其错误地分到歌声部分导致歌声分离不完全。MFCC反复结构能够将歌曲中的反复部分和非反复部分分离出来,但是分离出的歌声在低频处含有未分离出的背景音乐。单独的歌声分离算法不能很好地将歌声与背景音乐分开,因此本文将RPCA方法和MFCC反复结构进行结合并构建了掩蔽模型,实验也证明了本文方法在歌声分离方面的优越性。
对于RPCA算法分离出的歌声中含有未分离背景音乐声源的重复度要比歌声高的这一特性,结合梅尔频率倒谱系数反复结构能将反复部分和非反复部分分离开,本文提出了一种基于鲁棒主成分分析(RPCA)和梅尔频率倒谱系数(MFCC)反复结构的音乐分离算法。该算法能将稀疏矩阵中残留的背景音乐声源和歌声进一步分离出来,对于MFCC反复结构在低频处歌声分离效果差的问题也有进一步的改进。其中,在提取反复结构中反复周期的过程中使用了MFCC参数建立的相似矩阵来代替传统的节奏谱,不仅提高了模型的泛化能力,而且更加符合音乐的实际情况。
1 鲁棒主成分分析与梅尔频率倒谱系数反复结构算法理论
1.1 鲁棒主成分分析(RPCA)算法理论
RPCA也是基于重复是音乐的基本原理这一理念而开发的。假设音乐伴奏等级较低,变化较小,而人声变化较大,但是在音频混合中比较稀疏。在分解的过程中就演变成了式(1)中的凸优化问题[19],但是有些乐器声源和歌声一样也表现出稀疏性,所以分离后的歌声里中往往含有被错误分到稀疏矩阵的音源,这使得歌声分离性能不佳。
式中:D为原始混合信号矩阵,A为低秩矩阵,E为稀疏矩阵,λ为低秩矩阵和稀疏矩阵之间的折中系数,‖ · ‖*表示核范数,‖ · ‖1表示1范数。
对于式(1)中使用了非精确的增广拉格朗日乘子[20](Inexact Augmented Lagrange Multiplier)的方法来对凸优化问题进行求解。首先是构造拉格朗日函数,然后通过增加惩罚项将有约束的问题转化为无约束问题:
输入:观测矩阵D,λ。
(1)Y0=D/J(D);E0=0;μ0>0;ρ>1;k=0。
(2)当算法不收敛时执行下面步骤。
(3)通过式(3)~(5)求解Ak+1。
(4)通过式(6)、(7)求解Ek+1。
(5)求解Yk+1。
(6)更新μk至μk+1。
(7)迭代次数k更新为k+1。
(8)如果收敛则结束迭代。
输出:(Ak,Ek)。
在以上算法流程中,ρ是μ更新时的步长,k为迭代的次数,svd(·)表示奇异值分解,U和V表示奇异值分解得到的正交矩阵,S为对角矩阵。
1.2 梅尔频率倒谱系数(MFCC)反复结构算法理论
Rafii等[6]提出的基于反复结构的音乐分离算法(REPET)模型是建立在节奏谱的基础上的,在节奏谱的获取中采用能量信息作为特征。与传统的节奏谱比较,MFCC参数能体现全局性能并且包含着音乐的整体信息,但是也存在歌声在低频处不能完全分离的缺点。MFCC反复结构算法分离模型如图1所示。

图1 MFCC多反复结构分离模型示意图Fig.1 Diagram of MFCC multi-repeated structure separation model
首先,将输入信号通过一个高通滤波器来提升高频部分并且使得信号频谱变得平坦,再对信号进行加窗分帧以及快速傅里叶变换(Fast Fourier trans‐for,FFT),随后将FFT得到的频谱通过一个梅尔滤波器组来将谐波作用消除掉,使得原先语音的共振峰更突出,然后对滤波器组的输出取对数,分别计算对数能量和提取MFCC系数,然后根据MFCC系数来计算其一阶差分和二阶差分,最后将一阶差分、二阶差分、MFCC系数和对数能量进行组合得到MFCC特征参数。一阶差分dt、二阶差分C(n)、MFCC系数和对数能量s(m)的计算式分别为式(9)、(10)和(11)。
式中:dt为第t个一阶差分,Ct为第t个MFCC 系数,Q为MFCC 系数阶数,K为一阶导数的时间差,将式(9)结果再代回式(9)就能到二阶差分。
式中:m为第m个Mel滤波器(共有M个),n表DFT后的谱线个数。
式中:E(j)为每一帧谱线的能量,j为频域中的第j条谱线。接下来对MFCC特征参数进行相似运算,并且通过余弦相似性计算出相似矩阵SMFCC,表达式为
式中:i为频率点,n为MFCC参数维数,j为帧数,L(i,ja)、L(i,jb)为第i帧、第ja谱线和第i帧、第jb谱线下MFCC 参数矩阵。图2 为MIR-1K 数据库中amy_1_01 .wav音乐片段的MFCC相似矩阵。
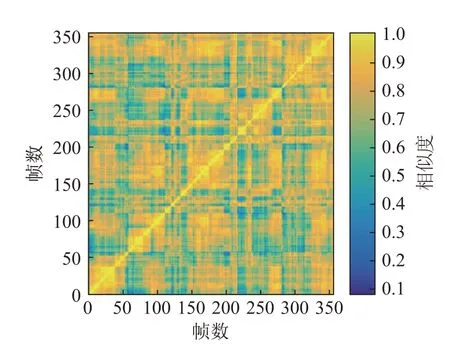
图2 MIR-1K中amy_1_01.wav音乐片段的MFCC相似矩阵Fig.2 The MFCC similarity matrix of amy_1_01.wav music clip in MIR-1K
然后,根据求得的相似矩阵SMFCC将相似度接近的部分拼接在一起,找到在幅度谱V中对应的片段并且进行中值滤波得到相应帧处的反复结构模型S(i,j),计算公式为
式中:i为频率点,j为帧数,h为片段数量,median(·)表示中值滤波器,V[i,Jj(l)]为频率点i的第l个重复片段的信号幅度谱,Ji=[J1,…,Jl],是具有相同反复结构片段组成的向量。当寻找相似片段时,具体包括如下限制:
(1)反复结构的最大长度、最小长度需要通过音乐片段的长度来限定;
(2)需要通过反复片段持续的时间来确定门限;
(3)根据相似矩阵确定片段之间的相似度,相似度大于门限值的两个片段为相似片段。
文中设置的相似度门限值为0.6,如图2所示,如果两个片段相似度大于或等于0.6的就会被认为是一个重复片段,整合在一起记作J。
2 本文所提出的歌声分离方法
2.1 掩蔽模型
图3所示为生成最终掩蔽矩阵的流程图。首先用低秩矩阵A或稀疏矩阵E的幅度谱与对应的反复结构模型SA或SE比较,并且取最小值来得到反复部分的幅度谱,其中反复部分对于稀疏矩阵E来讲就是歌声中重复度更高的背景音乐,对于稀疏矩阵E来讲就是除去了残留人声后的背景音乐。最后使用低秩矩阵E的幅度谱来归一化对应的背景音乐(反复部分)幅度谱,对于低秩矩阵A也是如此。最终得到了掩蔽矩阵M1和M2。
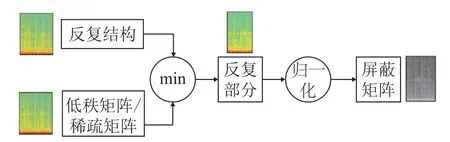
图3 掩蔽模型建立流程图Fig.3 Flow chart of masking model establishment
文献[5]中提到,可以假设非负的谱图是一个非负的重复谱图(反复部分)和一个非负的非重复谱图(非反复部分)组成的。以求稀疏矩阵中反复部分的掩蔽矩阵为例,则有:
式中:V1为稀疏矩阵中含有未分离背景音乐的幅度谱(反复部分),V′1为二次分离后歌声的幅度谱(非反复部分),Ek为稀疏矩阵的幅度谱。
接下来使用稀疏矩阵的幅度谱Ek与求出的反复结构模型SE进行比较取最小值来得到稀疏矩阵中未分离背景音乐的幅度谱V1,计算公式为
式中:Ek(i,j)为稀疏矩阵E中对应频率为i、帧数为j时的幅度谱,V1(i,j)为稀疏矩阵中未分离背景音乐中对应频率为i、帧数为j的幅度谱,SE(i,j)为频率为i、帧数为j时对应的反复结构模型。
最后通过稀疏矩阵幅度谱Ek来归一化V1得到稀疏矩阵对应的掩蔽矩阵M1,其表现为:属于反复片段的部分为1,其余为0,计算公式为
2.2 本文所提出的方法描述
本文提出的基于RPCA和MFCC反复结构的音乐分离方法,流程图如图4所示。假设背景伴奏具有低秩的特性,歌声具有稀疏的特性[10],对输入的混合音乐信号做短时傅里叶变换,然后分别提取相位谱和幅度谱,对幅度谱进行RPCA分解,成为含有背景音乐的低秩矩阵Ak以及含有歌声的稀疏矩阵Ek。然后结合相位得到对应的时域信号SA和SE。
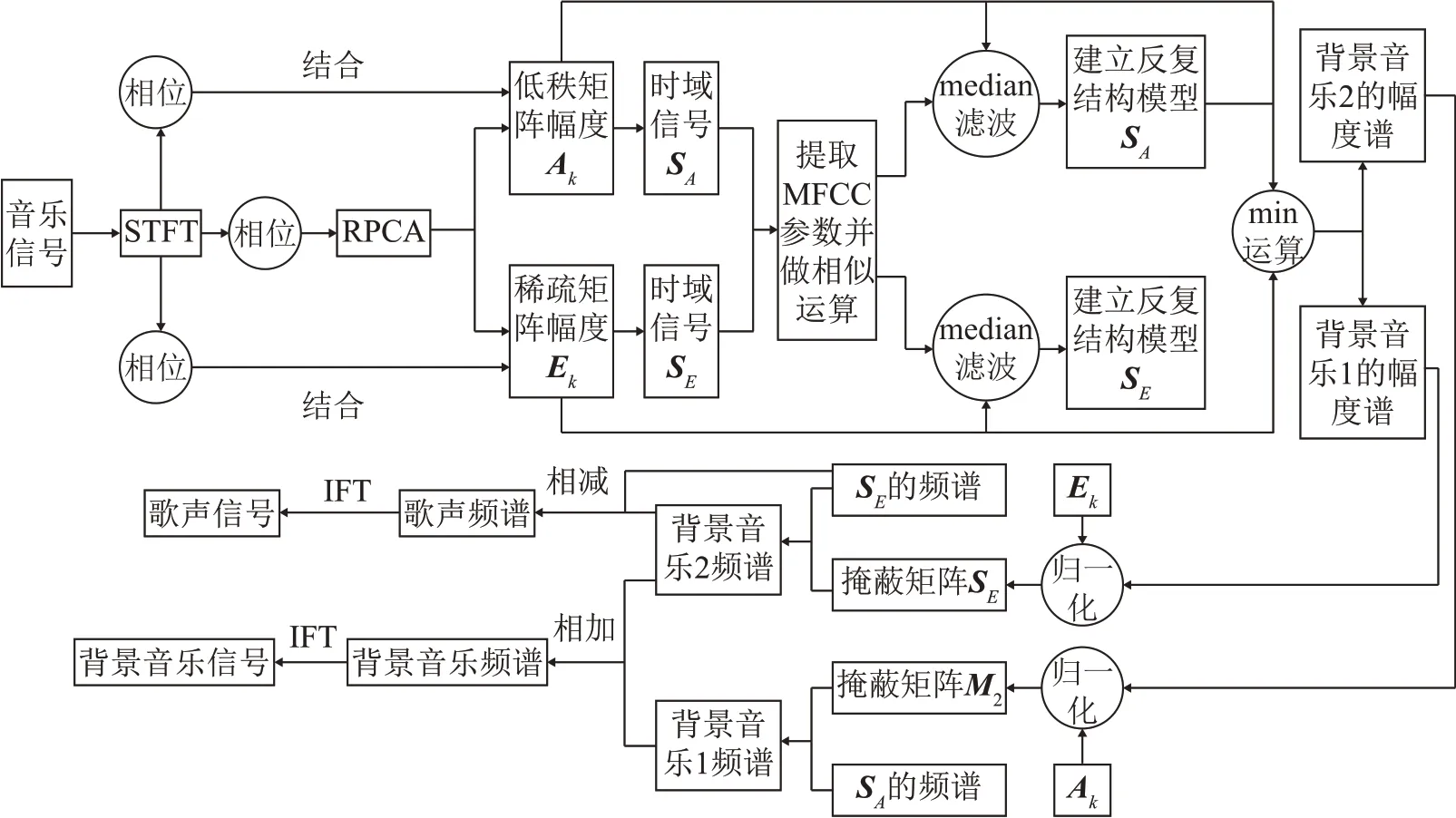
图4 本文提出的分离模型流程图Fig.4 The flow chart of the separation model proposed in this paper
接下来,分别对SA和SE提取MFCC 特征参数并且通过余弦相似性计算其相似矩阵SA-MFCC(ja,jb)和SE-MFCC(ja,jb),计算公式分别为
本文使用39 维MFCC 参数而不是只使用MFCC系数,它包含1维能量信息、12维梅尔系数以及它们的一阶差分、二阶差分。
一阶差分和二阶差分参数反映出了语音的动态特性,而标准的MFCC系数则反映出了语音的静态特性,所以将这三者结合起来能够有效提升系统的识别性能。一段语音通过Mel滤波器组后它的音调或音高不会呈现在MFCC参数内,这使得以MFCC作为特征的系统并不会受到输入语音的音调不同而有所影响,这也间接地提升了模型的泛化性。
然后通过相似矩阵与对应幅度谱比较来提取相似片段并进行中值滤波,在比较时幅度谱上与相似矩阵偏差很小的部分将构成一个重复模式并将被中值滤波捕获,相反,偏差很大的部分将不会构成一个重复模式,并会被中值滤波移除。最后将所有的重复模式结合起来分别建立反复结构模型SA和SE计算公式分别为
这里的中值滤波实际使用的是几何平均值,文献[7]发现几何平均值能更好地区分重复和非重复结构。
接下来,分别计算低秩矩阵A和稀疏矩阵E的幅度谱将其与对应的反复结构模型进行比较得到背景音乐1和2的幅度谱V1和V2,这里使用最小值函数进行比较,计算V1,V2公式分别为
通过低秩矩阵幅度谱Ak来归一化V1,用稀疏矩阵幅度谱Ek来归一化V2,分别得到掩蔽矩阵M1和M2,掩蔽矩阵中属于反复片段的部分在M1和M2中的值为1,其他情况为0,M1、M2的计算公式为
最后分别通过掩蔽矩阵M1和M2与低秩矩阵的频谱XA和XE相乘得到背景音乐1和2的频谱,歌声的频谱为稀疏矩阵频谱减去背景音乐2的频谱,最后总的背景音乐频谱为背景音乐1的频谱和背景音乐2中除去歌声后的频谱的和,最后做傅里叶逆变换得到最终的背景音乐信号和歌声信号。
2.3 本文提出方法的具体步骤
(1)计算输入混合音乐信号的短时傅里叶变换,记为D,并且提取其相位:
(2)使用上文中的非精确拉格朗日乘子算法来优化式(2),得到Ak和Ek。
(3)将得到的Ak和Ek与式(25)结合得到:
式中:m=1…n1,n=1…n2,然后进行短时傅里叶逆变换,得到经过RPCA分离后的背景音乐时域信号SA和歌声时域信号SE。
(4)根据式(9)、(10)和(11)分别对SA和SE提取MFCC特征参数,并且通过式(12)和式(17)、(18)分别计算出其相似矩阵。
(5)通过式(7)和式(19)、(20)分别计算反复结构模型。
(6)假设反复部分与非反复部分的幅度谱是相互独立的,则有:
式中:V1为稀疏矩阵中含有背景音乐部分的幅度谱;V′1为二次分离后歌声的幅度谱;V2为反复部分;V′2为非反复部分。
(7)通过式(15)和式(21)、(22)计算得到背景音乐1和背景音乐2的幅度谱V1、V2。
(8)通过式(16)和式(23)、(24)计算得到背景音乐1和背景音乐2的掩蔽矩阵。
(9)掩蔽矩阵与频谱XA和XE相乘并且进行傅里叶逆变换,得到最终背景音乐和歌声:
式中:F-1为傅里叶逆变换,为最终分离得到的歌声信号,为最终分离得到的背景音乐信号。
3 实验结果与分析
3.1 实验数据集
本文使用公开的数据集MIR-1K[21]对文中提出的算法进行性能评估。该数据集是由Hsu和Jang收集,它包含有1 000首音乐片段,音乐片段的采样率为16 kHz,长度为4~13 s,均是由一些歌唱业余爱好者演唱的。背景音乐与歌声分别存入左右声道。
3.2 分离结果性能评估指标
3.2.1 盲源分离工具箱
在结果性能评估阶段通常使用的是BSS_EVAL[22]工具箱来衡量分离方法的性能。假设分离后的估计信号为,可将其分解为4 个部分,数学表达式为
式中:starget(t)表示目标信号源的部分;einterf(t)表示由其他信号源引起的估计误差;enoise(t)表示噪声对观察信号产生的干扰误差;eartif(t)表示算法本身产生的系统噪声误差。
在一首歌曲中,相对于歌声和背景音乐之间的相互干扰,噪声对音乐的影响可以忽略掉,所以删去式(32)中的误差enoise(t)。剩下的三个误差分别形成了三个衡量分离性能的参数,分别为源干扰比(Source to Interference Ratio,SIR)RSI、源偏差比(Source to Distortion Ratio,SDR)RSD和源伪影比(Source to Artifacts Ratio,SAR)RSA,计算公式为
式中:RSI、RSD和RSA分别用来衡量算法的分离度、算法的噪声性能和算法的鲁棒性。三个值越高也就代表算法的性能越好。
3.2.2 主观评价标准
主观评价标准(Mean Opinion Score,MOS)是采用打分的形式来评价语音质量的标准。它是由所有听众对每一段音乐所给出的分数的算术平均数,计算公式为
式中:N为听众人数,Rn为特定乐曲的个别MOS,即分离的背景音乐或歌声。打分形式采用满分为5分的标准:5分表示听感优秀;4分表示听感良好;3分表示听感尚可;2分表示听感较差;1分表示听感劣质。
3.3 实验结果与比较
在MIR-1K 数据集中任意抽取一首音乐片段,使用本文所提方法进行分离。以abjones_1_01.wav为例。图5为原始歌声和使用三种方法分离出的歌声语谱图。

图5 原始歌声和使用三种分离算法分离出的歌声语谱图Fig.5 Spectrograms of the original song and the voices separated by three separation algorithms
原始歌声和使用三种方法分离出歌声的时域波形如图6所示。
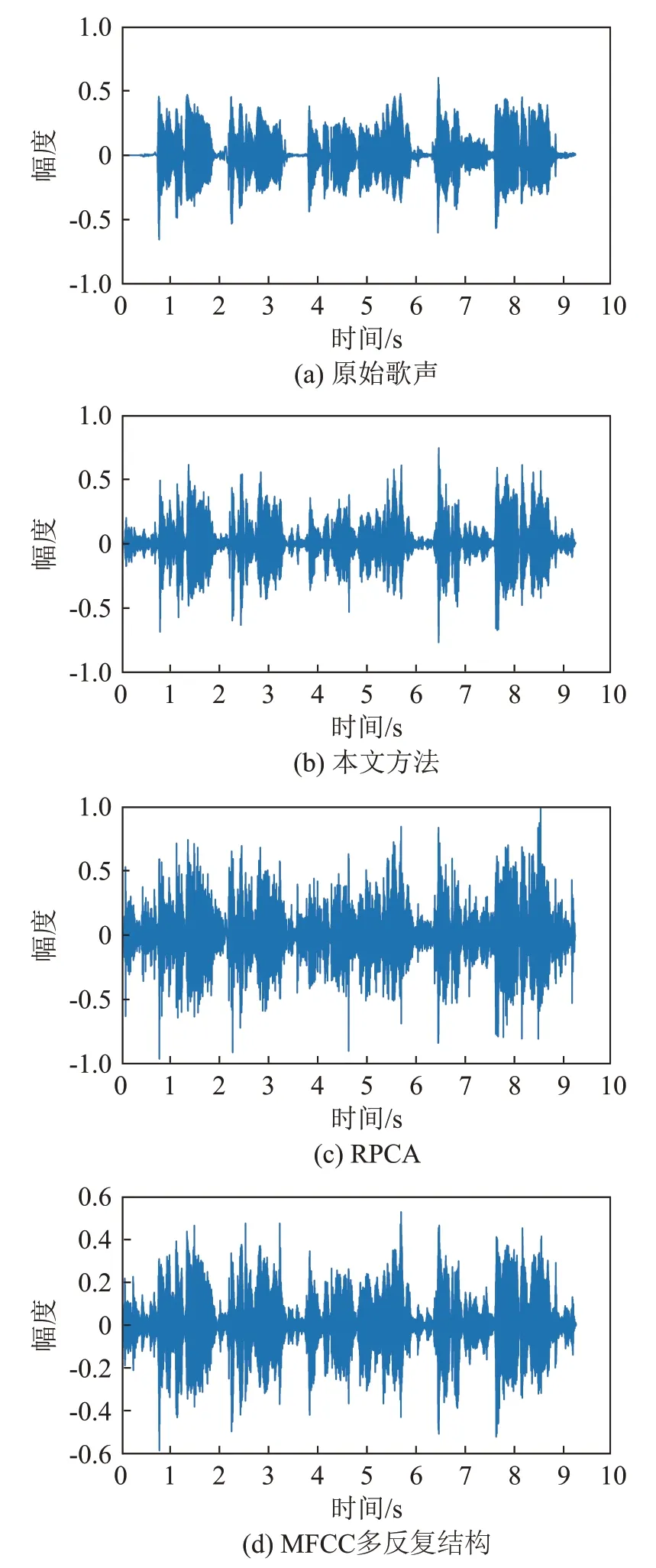
图6 原始歌声和采用三种分离算法分离出歌声的时域波形Fig.6 Waveforms of the original song and the voices separated by three separation algorithms
比较图5(a)和图5(c)可以看出,使用RPCA 分离后的歌声中混有未能成功分离的部分背景音乐。比较图5(a)与图5(d)可以看出,使用MFCC多反复结构在频率3 000 Hz以下分离出的歌声含有着较多的背景音乐的能量,尤其是在0~1 000 Hz 内,分离的效果较差。对比图5(b)、图5(d)和图5(c)可以看出,使用本文提出方法分离后的歌声在MFCC多反复结构缺点(即在低频时分离效果不理想)方面有了进一步的提升,同时相比于RPCA算法,本文提出方法分离出的歌声语谱图中含有的背景音乐的能量明显减少。
由图6可以看出,使用RPCA分离出的歌声波形相比于原始波形有着明显的失真,非语音段毛刺幅度很大;使用MFCC多反复结构分离出的歌声波形虽然相比于RPCA 非语音段的毛刺幅度变小了,但是歌声段的波形和原始波形不够吻合;本文提出的方法分离出的歌声波形相比于RPCA方法,在语音段与非语音段的提升较明显,相比于MFCC多反复结构来说,与原始歌声波形相比,语音段波形吻合度得到了进一步提升,非语音段的毛刺的幅度变得更平稳。
为了进一步说明本文方法相对于MFCC多反复结构框架和RPCA的优越性,从MIR-1K的1 000首音乐片段中随机选取了5首音乐片段进行分离后计算其SDR、SIR 和SAR(抽取的音乐片段为:“yi‐fen_3_11.wav”“Tammy_1_04.wav”“Leon_7_13.wav”“abjones_3_09.wav”“bobon_5_07.wav”),结果如图7所示。

图7 不同算法对5首音乐片段所分离出的歌声的性能比较Fig.7 Performance comparison between the voices separated by different algorithms from 5 music clips
由图7可以看出,本文提出的方法在三个分离指标(即SDR、SIR 和SAR)上均优于MFCC 多反复结构和鲁棒主成分分析(RPCA)。在SDR 值上相对于RPCA 算法最高有5 dB 左右的提高,相比于MFCC多反复结构最高也有接近3 dB的提高,这说明了本文算法分离出的歌声的整体失真情况更小。SIR 的提升比较明显,相比于其他两种算法有2~11 dB的提高,这也说明本文提出的算法的歌声分离度更好。
本文还进行了主观听感测试(MOS),选取10个被试,其中5 个男生一组,5 个女生一组。分别对MFCC多反复结构、RPCA和本文提出方法得到的歌声和背景音乐的分离质量进行评价,结果如表1所示。
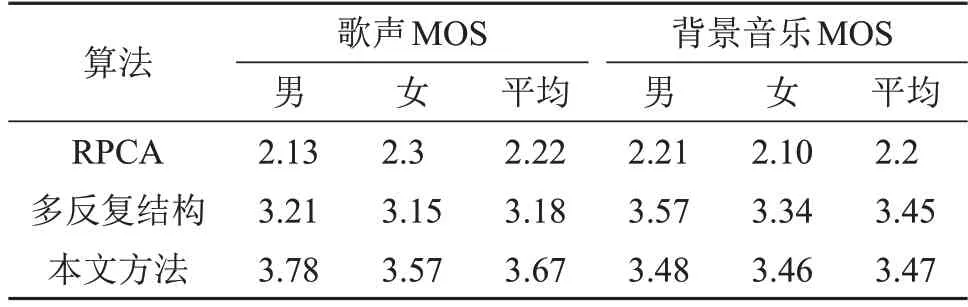
表1 不同算法对随机5首音乐片段的MOS测试结果对比Table 1 Comparison of MOS test results of 5 random music clips by different algorithms
从主观听感测试可以看出,本文算法能够很好地分离出歌声和背景音乐,虽然分离出来的歌声还是不够纯净,伴有着微小的音乐噪声,但是相比于其他两种算法分数有较大提升。对于背景音乐本文算法的听感明显优于RPCA方法,相比于多反复结构听感也有一定的提升。
本文还选取了MIR-1K 数据库中1 000 首音乐片段使用不同的算法来进行处理,分别计算其歌声与背景音乐的SDR、SIR 和SAR。对比算法为REPET算法、多反复结构以及RPCA算法。比较结果如表2和表3所示。通过表2和表3可以看出,在分离背景音乐时,本文算法相比于其他三种算法的平均SIR 提高了1~2 dB,说明了本文方法分离的背景音乐分离度好。在分离歌声时,本文算法相比于其他三种算法的平均SIR 提高了约3~7 dB,说明本文方法的歌声分离度得到了很大的提高,算法鲁棒性也更好。平均SDR也提高了1~4 dB,说明分离出的歌声信号整体失真更小。
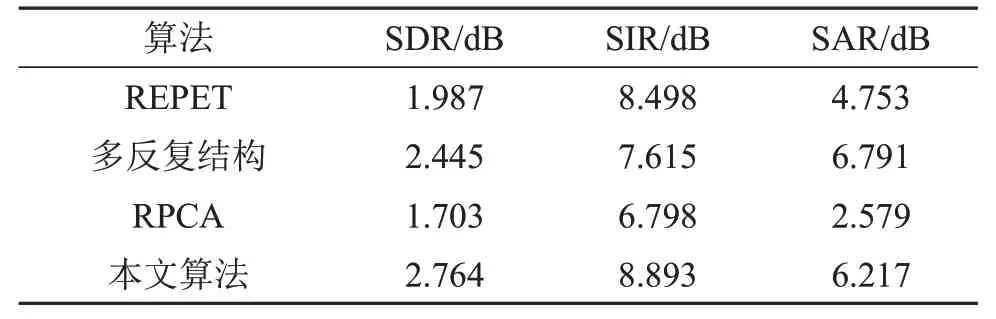
表2 不同方法对1 000首音乐片段背景伴奏分离性能的比较Table 2 Comparison of average results of background accompaniment separation performance for 1 000 music clips by different algorithms
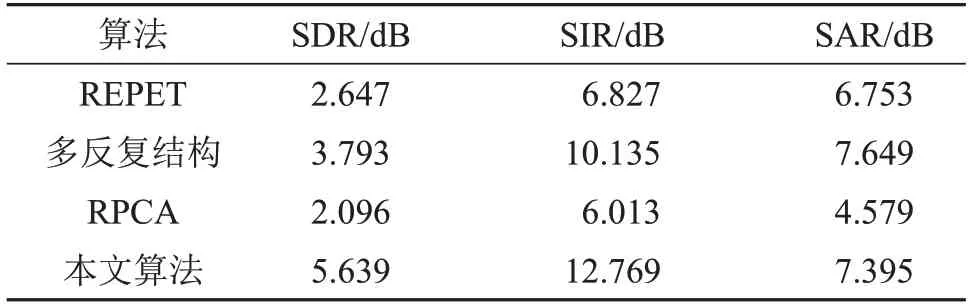
表3 不同方法对1 000 首音乐片段歌声分离性能的平均结果比较Table 3 Comparison of average results of singing voice separation performance for 1 000 music clips by different algorithms
4 结论
基于单一的传统歌声分离方法难以将歌声和伴奏彻底分离的问题,本文提出了一种基于RPCA和MFCC反复结构的歌声伴奏分离方法。该方法在使用RPCA 将混合音乐信号分解为低秩矩阵(背景音乐部分)和稀疏矩阵(歌声部分)时,由于有些乐器也表现出和歌声一样的稀疏性,使得这部分乐器音源会被错误地分到歌声中。这部分乐器音源的重复性要比歌声要高,所以通过提取的MFCC参数来建立反复结构模型,然后结合最后构建的掩蔽模型来进一步将混在歌声中的背景音乐分离出来。实验结果表明,单独使用MFCC反复结构会存在歌声在低频处分离效果不佳的问题,本文提出将两者结合可以有效地改善RPCA 和MFCC 反复结构中存在的问题。
实验在对MIR-1K 数据库中1 000 首音乐片段进行处理后,本文方法较其他3 种算法的平均SIR最高提高了约7 dB,说明本文方法的歌声分离效果很好,同时平均SAR 最高提高了约3 dB,也说明了本文方法的鲁棒性较好。平均SDR 最高提高了约4 dB,说明本文方法分离出的歌声失真度是最小的。从数据和声谱图来看,本文方法能够在RPCA分离的基础上将残留在歌声中的背景音乐成功分离出来,同时也改善了MFCC多反复结构在低频处歌声分离性能不理想的情况。综上所述,本文方法能够有效分离歌曲中的歌声和背景音乐。

