Coalitional game based resource allocation in D2D-enabled V2V communication

MA Piming, ZHAO Peng, BAI Zhiquan,*, DONG Xu,YANG Xinghai, and KWAK Kyungsup

1.Shandong Provincial Key Lab of Wireless Communication Technologies, School of Information Science and Engineering,Shandong University, Qingdao 266237, China; 2.School of Information Science and Technology, Qingdao University of Science and Technology, Qingdao 266100, China; 3.Graduate School of Information Technology and Telecommunications, Inha University, Incheon 22212, Korea

Abstract: The joint resource block (RB) allocation and power optimization problem is studied to maximize the sum-rate of the vehicle-to-vehicle (V2V) links in the device-to-device (D2D)-enabled V2V communication system, where one feasible cellular user (FCU) can share its RB with multiple V2V pairs.The problem is first formulated as a nonconvex mixed-integer nonlinear programming (MINLP) problem with constraint of the maximum interference power in the FCU links.Using the game theory, two coalition formation algorithms are proposed to accomplish V2V link partitioning and FCU selection, where the transferable utility functions are introduced to minimize the interference among the V2V links and the FCU links for the optimal RB allocation.The successive convex approximation (SCA) is used to transform the original problem into a convex one and the Lagrangian dual method is further applied to obtain the optimal transmit power of the V2V links.Finally, numerical results demonstrate the efficiency of the proposed resource allocation algorithm in terms of the system sum-rate.

Keywords: coalitional game, vehicle-to-vehicle (V2V) communication, successive convex approximation (SCA), resource block(RB) allocation, power allocation.

1.Introduction

In order to reduce the traffic congestion, improve the driving safety, and provide the in-vehicle infotainment services, vehicular communication has gained considerable attention recently from both academic and industrial communities [1-3].Device-to-device (D2D) communication is able to realize the direct message transmission between two adjacent users by reusing the cellular resources, which is particularly suitable for the vehicle-tovehilcle (V2V) communication scenarios [4,5].

The resource allocation has been extensively studied to mitigate the interference in both D2D underlaying cellular systems and D2D-enabled vehicular networks.In [6],a joint fair resource allocation policy was investigated under channel gain uncertainty, which aimed to improve the sum-rate of the D2D system as well as guarantee the quality of service (QoS) of the cellular users (CUs).In[7], a spectrum sharing and power allocation scheme based on the large-scale fading was proposed in vehicular network with D2D communication to maximize the minimum ergodic capacity, while ensuring the reliability requirement of each V2V link.However, the above resource allocation mechanisms mainly focus on the case that one channel is reused by at most one D2D pair.To improve the spectrum efficiency, multiple D2D pairs are permitted to reuse the same resource block (RB), but the mutual interference among them may cause serious performance degradation.Nevertheless, well-designed resource allocation policies have the potential to dramatically reduce the mutual interference among the D2D pairs and improve the system performance [8-13].The authors in [8] discussed a spectrum and power resource allocation problem in energy harvesting powered D2D communication cellular network with multiple D2D links reusing the spectrum resource of one CU, where two algorithms were proposed respectively to solve the resource optimization problem.Liang et al.proposed a graph-based algorithm to divide the highly interfering V2V links into different clusters before spectrum allocation and power control in D2D-based vehicular communication networks [12].

Recently, the use of coalitional game to solve the resource allocation problem has been intensively discussed.Song et al.in [14] have shown the applications of game-theoretic models, including coalitional game model, in the radio resource allocation problems for the D2D communication.In [15], a suboptimal resource allocation scheme based on coalition game was proposed to maximize the minimum throughput of the V2V links,which can ensure the requirements of the minimum throughput from the vehicle to infrastructure (V2I) links.Li et al.have proposed a coalitional game based fair uplink resource allocation algorithm in [16] for cellular network to reduce the mutual interference among vehicular links.In this paper, we employ a coalition formation game to alleviate the mutual interference among the V2V links in the D2D-enabled V2V communication.

We investigate the resource allocation based on coalitional game in the D2D-enabled V2V communication,where multiple V2V pairs and a feasible CU (FCU) can share the same RB.A resource allocation strategy has been proposed to maximize the sum-rate of all the V2V links and guarantee the QoS of the FCUs considering that the interference power from V2V links to FCU links is limited.The main contributions of this work focus on the following parts.

(i) To improve the spectrum efficiency, an FCU’s RB can be allocated to multiple V2V links in the D2Denabled V2V communication system.A joint RB allocation and power optimization problem is formulated as a nonconvex mixed-integer nonlinear programming(MINLP) problem which can be solved by game theory and successive convex approximation (SCA) method.

(ii) Two coalition formation algorithms are presented to achieve the optimal RB allocation.A coalition formation algorithm is proposed to partition the V2V links so that the interference power within the V2V links can be minimized.To obtain the minimum interference power from the FCU links to the V2V links, we bring out another coalition formation algorithm to select the FCU’s RB for the V2V links in each V2V group.

(iii) To solve the nonconvex power optimization problem, we adopt the SCA method and obtain the tight lower convex bound to transform the origin problem to a convex one, and then the Lagrangian dual method is employed to achieve the optimal V2V transmit power.

The remainder of the paper is organized as follows.Section 2 presents the system model of the D2D-enabled V2V communication scenario and the problem formulation about maximizing the sum-rate of V2V links.In Section 3 and Section 4, the RB allocation based on the coalition formation game and the power optimization based on the SCA method are illustrated, respectively.Section 5 gives the convergence and complexity analysis of our proposed algorithms.Section 6 provides the numerical results to demonstrate the performance of the proposed resource allocation strategy in the D2D-enabled V2V communication system.Finally, we draw the conclusions in Section 7.

2.System model and problem formulation

2.1 System model

We consider a D2D-enabled V2V communication scenario in Fig.1, which consists of an evolved Node B(eNB), multiple orthogonal CUs andKV2V pairs.Each CU can occupy a dedicated RB for uplink transmission from the CU to the eNB.According to the signal-to-interference-plus-noise ratio (SINR) requirement in the CU uplinks,MCUs are assigned to share their RBs for the V2V link transmission from V2V transmitter (V2V Tx)to V2V receiver (V2V Rx) and each selected CU is called the FCU.Each V2V link is only permitted to reuse at most one RB, and multiple V2V links can reuse the same FCU’s RB to improve the spectrum efficiency.This scheme will introduce mutual interference among the V2V links and the FCU uplinks which is illustrated in the elliptical area of Fig.1.To better describe our model, we define the channel parameters from the source to the destination in Table 1.

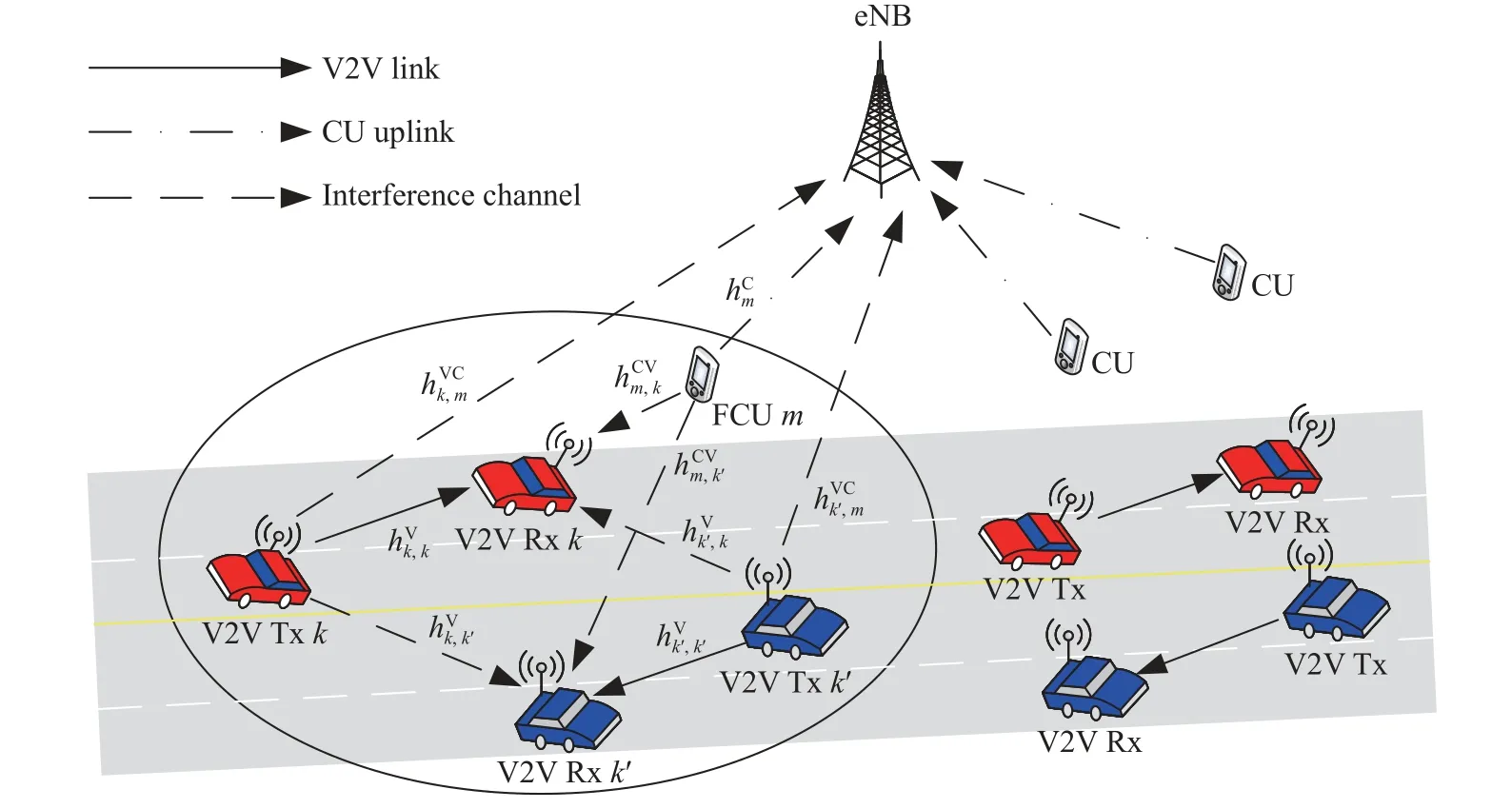
Fig.1 System model of D2D-enabled V2V communication

where σ2is the power of the additive white Gaussian noise.Thus, the received SINR at V2V Rxkassociated with FCUmcan be given by

where Θ{k} is denoted as the set Θ withoutk.Assuming that each V2V link has unit bandwidth, the transmission rate of the V2V Rxkreusing the RB of FCUmcan be expressed as

The eNB is fully responsible for the resource allocation, so it needs to obtain the certain channel state information (CSI) through the utilization of the control signal feedback mechanism.The CSI of the links connected with the vehicles changes rapidly due to the high mobility in the vehicular environment, so timely and frequent feedback of the full CSI may lead to heavy signaling overhead.Thus, we assume that the eNB only acquires the large-scale fading information, such as the path loss and shadowing, which can significantly alleviate the signaling overhead.Therefore, this work mainly focuses on the resource allocation considering the large-scale fading condition.

2.2 Problem formulation

The infotainment applications require large throughput to transmit the information.When the V2V links reuse the RBs of the FCUs, we should guarantee the QoS of the FCUs.Therefore, we should maximize the sum-rate of all the V2V links while restraining the aggregated interference of the FCUs caused by the V2V links.From the perspective of the V2V link partitioning and FCU selection,the optimization problem can be formulated as

In problem (4), the optimization variables αk,mandPVkare binary and continuous variables, respectively, for anyk∈Θ,m∈Ω, where the objective function is non-convex with affine constraints.Consequently, the problem(4) is MINLP problem involving continuous and discrete variables [17], which is difficult to jointly optimize the continuous and discrete variables in the polynomial-time.Therefore, we propose a heuristic scheme to divide the MINLP problem into the RB allocation subproblem and the power allocation subproblem.

3.RB allocation based on coalition formation game

3.1 V2V link partitioning

For V2V link partitioning, the coalitional game is employed to partition the highly interfering V2V links into different groups in order to reduce the interference power between the V2V links which reuse the same RB.The interference level of the corresponding V2V link can be measured by its channel gain [12].For instance, the channel gainis denoted as the interference level from the V2V Txkto the V2V Rxk′, for ∀k,k′∈Θ, andk≠k′.Then, the V2V link partitioning problem can be written as

where constraint (12) sets the V2V link partitioning indicator to be an integer 0 or 1, constraint (13) guarantees that each V2V link can only join one group and constraint (14) indicates that each group contains as least one V2V link.

In this subsection, the V2V link partitioning problem is modeled as a coalitional game with the transferable utility [18], where the V2V links tend to form the partition so that the mutual interference of the V2V links within the same group can be minimized.Then, a coalition formation algorithm for V2V partitioning is designed.

Based on the game theory, the pair (Θ,U) represents a coalitional game with transferable utility, where Θ is a set of game players andUis a utility function for every coalitionCn∈Ψ , andU(Cn) is a real number to quantify the contributions of coalitionCn.

The smaller the total interference of the V2V Rxk′received from the other links within the same coalition,the greater its individual contribution is.We define the utility function of the coalitionCnasU(Cn)=

The key mechanism in the coalitional game is that each player chooses to join or leave a group based on the welldefined preference and operation that may achieve the goal of maximizing the system total utility function.We utilize the concepts of the preference order and switch operation to elaborate this process in detail.

Thatis,ifplayerkiswillingtojoincoalitionCn′rather tha nCn,thenew coalitional partitionwill be formed after the switch operation is executed.Based on the preference order and switch operation defined above, the ultimate propose of the coalitional game is to maximize the total utility rather than the individual contributions of players.Moreover, with the increasing switching operations, the total utility strictly increases during the formation of the partitions.

Algorithm 1 Coalition formation algorithm for V2V partitioning 1: Generate a random coalitional partition for the V2V link set and the number of V2V links is ;Ψcur=Ψini num=0 Ψini Θ K 2: Set the current coalitional partition and;3: repeat k ∈Θ Cn ∈Ψcur 4: Uniformly and randomly choose a player , and denote its current coalition as ;Cn′ ∈Ψcur∪{∅} Cn′ ≠Cn 5: Uniformly and randomly choose another coalition with ;1 6: if the preference order is satisfied 7: then update the current partition set as using(15),num=0 Ψcur 8: and ;9: else num=num+1 10: ;11: end if num=10K 12: until.

3.2 FCU selection

For FCU selection, the coalitional game is further utilized to select an appropriate FCU for the V2V links in each group, while minimizing the interference power from the selected FCU to the V2V links.To improve the sum-rate of the V2V links, the eNB selects an appropriate FCU for each V2V coalition.Therefore, the interference from the selected FCU to the V2V coalition can be limited as small as possible.Then, the FCU selection problem can be written as (16), where constraint (17) sets the FCU selection indicator to be an integer 0 or 1, constraint (18) guarantees that the V2V links in each group can only reuse one FCU’s RB and constraint (19) indicates that each FCU’s RB can be reused by no more than one group.

On the basis of the V2V link partitioning, the FCU selection problem can be modeled as a coalitional game with transferable utility, in which the appropriate FCUs are selected to join the coalitions of the V2V links.

If the utility function brought by playermandm′respectively joining the coalitionDn′andDnis greater than that generated by the playermandm′respectively joining the coalitionDnandDn′with the increase of the total utility, the preference order 2 is given as

Given a coalitional partitionof the FCUs, if preference order 2 holds, the switch operation 2 is given as

Algorithm 2 describes the proposed coalition formation process of the FCU selection.During the coalition formation process, it is necessary to ensure that a coalition of the V2V links only allows one FCU to join in.The total utility of all the coalitions increases strictly monotonically with the increase of the switch operations.If a switching operation occurs under the preference order 2,the count of the consecutive unsuccessful switch operations num is set to be 0.Otherwise, num is increased by 1.When num is 10 times greater thanM, the partition converges to the final Nash-stable partition Φfin.

Algorithm 2 Coalition formation algorithm for reusable RB selection 1: Randomly select an FCU for the V2V links of each coalition, and add the remaining FCUs to the auxiliary coalition.Denote the randomly generated coalitional partition and the number of FCUs as and ,respectively;DN+1 Φini M 2: Set the current coalitional partition and;3: repeat m ∈ΩDn ∈Φcur Φcur=Φini num=0 4: Uniformly and randomly choose a player , and denote its current coalition as ;Dn′ ∈Φcur Dn′ ≠Dn m′∈Ω Dn′5: Uniformly and randomly choose another coalition with , and the player uniquely joining in this coalition is denoted as (if is the auxiliary coalition, we need to randomly select one from the other players);2 6: if the preference order is satisfied 7: then update the current partition set as using (20),num=0 Φcur 8: and ;9: else num=num+1 10: ;11: end if num=10M 12: until.

4.Power optimization based on SCA method

The coalitional game has been utilized to partition the V2V links and the appropriate FCU has been selected for the V2V links in each coalition.That is, α is a discrete constant matrix after we have determined the RB allocation.According to the coalition conceptionCnandDnin Section 3, we can rewriteas

We attempt to find the optimal power allocation for the V2V links and the power allocation problem (4) of the V2V links is further described as

The lower bound of the objective function of the problem (21) is obtained by the following inequality:

The problem (21) can be rewritten as a standard concave maximization problem with unique optimal solution as

The Lagrangian dual theory [21] is employed to solve the problem (27).The Lagrangian function of (27) is

where the component of the vectoris dual variable.

Then, the dual function becomes

The dual problem of (27) can be denoted asand solved by the sub-gradient iterative algorithm and the Lagrangian variable vector λ can be updated by the subgradient method as

where τn>0 is a sufficiently small step size,tis the iteration number and [·]+=max{0,·}.

We have constructed a concave function with the same function value and the same gradient which can be solved by setting the partial derivation ofto be 0 as

Then, the optimal solution of the concave function can be derived as

Based on [20], with the application of the SCA method and under the constraint of (29), the transmit power of the V2V linkkcan be updated according to (35) withk∈Θ,n∈Ξ and [x]ba=min{max{x,a},b}.

Algorithm 3 Power allocation algorithm based on SCA method 1: Initialize the maximum iteration number , and set the initial iteration number.˜PV= ˜P0 2: Give an initial feasible value as.3: repeat ˜γ(t)T t=1 k,n(˜PV) y(t)k,n z(t)k,n 4: Calculate , and by (23), (25) and (26)respectively.λ PV 5: Update and using (32) and (35), respectively.6: Update iteration number.t=T t=t+1 7: until the iteration number.

5.Convergence and complexity analysis

In Section 3 and Section 4, three algorithms are proposed to achieve the RB allocation and power optimization.And in this section, we will analyze the convergence and complexity of the proposed Algorithms 1, 2 and 3.

5.1 Convergence analysis

Based on the SCA method, Algorithm 3 is an iterative algorithm.And in each iteration, we build a concave function(27) whichhas thesamevalueandgradientas(21)atthe solutionpointPVthatisobtainedin the last iteration.Hence, the value of the objective function is increased in each iteration, and it is upper bounded with a given transmit power constraint.Thus, Algorithm 3 can be proved convergence [22].

5.2 Complexity analysis

In each iteration of Algorithm 1, the selected V2V link calculates the total utility of the current coalition and another possible coalition, respectively.Then, it makes a decision on whether to perform a switch operation or not.Thus, there is at most one switch operation to be considered in each iteration, and the complexity lies in the number of iterations.According to the above analysis, complexity of Algorithm 1 can be approximated as O(10K).Similarly, the complexity of Algorithm 2 is approximated as O(10M)[19].

As for Algorithm 3, the complexity of Step 4 and Step5 can be calculated as O (3KN) and O (N+K) in each iteration.Then, the complexity of Algorithm 3 is O (T(3KN+N+K)).

Since the three algorithms operate only once, the total complexity is approximated asO(T(3KN+N+K)+10K+10M).

6.Numerical results

In this section, we evaluate the effectiveness of the proposed resource allocation scheme in the D2D-enabled V2V communication.We assume that a multi-line freeway passes through a single cell and the eNB is located at the center of the cell as shown in Fig.1.Vehicles are dropped onto each lane according to the spatial Poisson process, and the vehicle density on each lane is determined by the speed [23].Kvehicles are randomly chosen from the generated vehicles as V2V transmitters, and the V2V receivers are selected from the nearest vehicle users corresponding to the V2V transmitters.The main system parameters in the simulation are listed in Table 2 and Table 3, respectively.

Table 2 Channel model parameters

Table 3 System parameters

Fig.2 and Fig.3 show the total utility function versus the iteration number in Algorithm 1 and Algorithm 2, respectively, under the condition ofv=100 km/s, γ0=6 dB,andImax=10-10mW.In the simulation, there are 36 V2V links divided into four coalitions, where the number of the FCU, which can be determined by the requirement of γ0, is 37.We can see that the total utility is monotonous with the increase of the iteration for both Algorithm 1 and Algorithm 2.In Fig.2, the total utility reaches its maximum number after the 635th iteration.When the count of the consecutive unsuccessful switch operations num is 360 , Algorithm 1 stops at the 994th iteration.Similarly,the total utility reaches its maximum number after the 249thiteration and when the count of the consecutive unsuccessful switch operations num is 370, Algorithm 2 stops at the 618th iteration, as Fig.3 shows.It is seen from Fig.2 and Fig.3, both algorithms will converge quickly in the early stage, which reflects the fast convergence of the two algorithms.

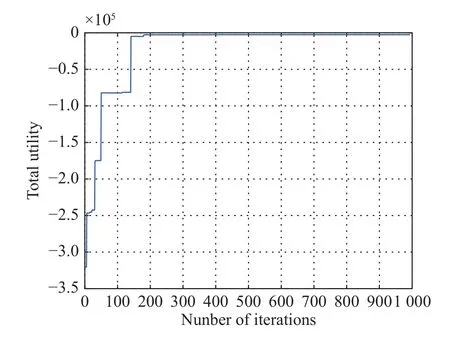
Fig.2 Total utility of Algorithm 1

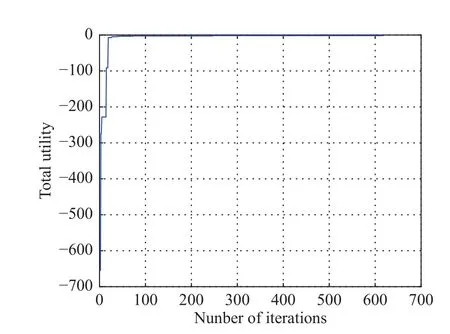
Fig.3 Total utility of Algorithm 2

Under the condition ofv=100 km/s, γ0=6 dB, andImax=10-10mW, the cumulative distribution function(CDF) of the number of switch operations for Algorithm 1 and Algorithm 2 are shown in Fig.4 and Fig.5, respectively, which demonstrates the convergence of the proposed coalition formation algorithms.ForN=4 andK=12, with Monte Carlo simulations, the coalition formation algorithms for the V2V partitioning and FCU selection can achieve the optimal solution within 28 and 20switch operations, respectively.For the combination ofN=6,K=18 , andN=8,K=24 as well asN=10,K=30, the two algorithms can converge to the Nash-stable partition through a finite number of switching.In addition, with the increase of the coalition number, the number of the combinations formed by the V2V links and FCUs increases, so does the number of the iterations converging to the Nash-stable partition.From Fig.4 and Fig.5,the two algorithms will reach the optimal solution within 70 and 35 switch operations, respectively, for all the four cases.

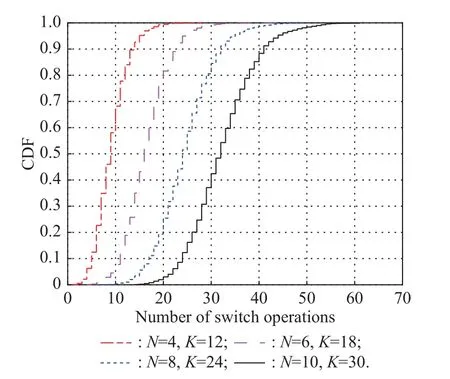
Fig.4 Convergence of Algorithm 1

Fig.6 shows the convergence of the Lagrange multipliers of the proposed power allocation scheme.In the simulation, the Lagrange multipliers are associated with the aggregated interference constraints of the selected FCUs in order to satisfy the QoS of FCUs.During the first20 iterations, the Lagrangian multipliers are quickly updated and the five Lagrange multipliers finally converge to a stable value after 147 iterations in Fig.6, which illustrates that theP˜Vand λ can converge to the optimal solutionP˜V∗and λ∗through a finite number of iterations for the proposed power allocation scheme.Note that Fig.6 just shows one random simulation, the convergence performance of Algorithm 3 depends on the initial value ofP˜0and the sufficiently small step size τn.In addition, the proposed scheme also converges quickly in the early stage.

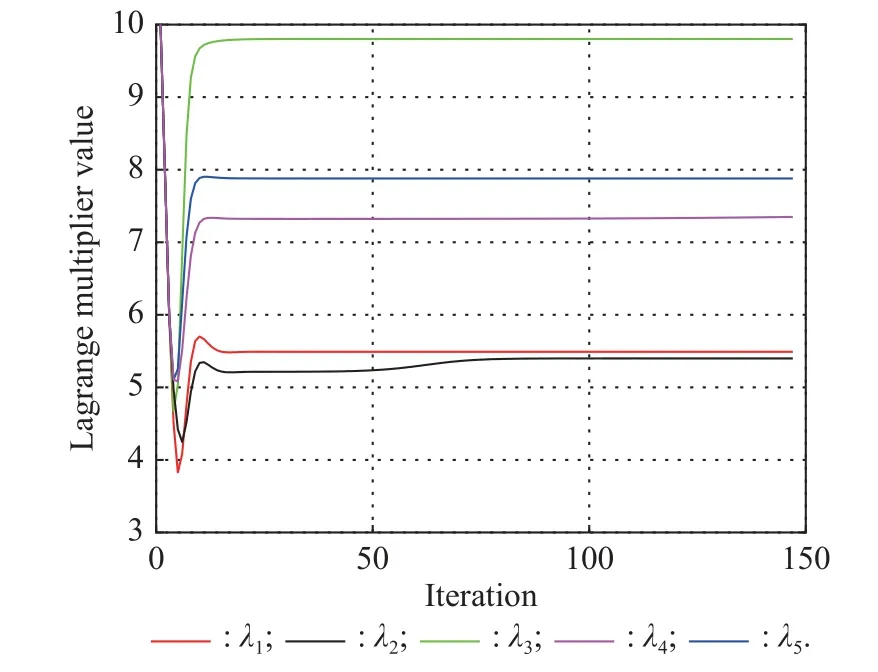
Fig.6 Convergence of Lagrange multipliers

The sum-rate of the V2V links versus the total number of the V2V linksKand V2V groupsNis shown in Fig.7.Under the condition ofv=100 km/h, γ0=6 dB andImax=10-10mW, we can observe that the sum-rate of the V2V links is increasing with the increase ofKfor fixedN, but the growth rate of the sum-rate gradually reduces.That is because, the increase of the V2V links will absolutely improve the sum-rate of the V2V links, but also increases the interference power among the V2V links and the FCU links which limits the growth rate of the sum-rate.For fixedK, the sum-rate of the V2V links also increases withN, because the more groups the V2V links are divided into, the lower interference power the V2V links will get.

Fig.8 demonstrates the sum-rate of the V2V links versus the interference power threshold of FCUs withv=100 km/h and γ0=6 dB.We find that the sum-rate of the V2V links increases with the interference power threshold of the FCUs for the four cases, because the V2V links are permitted to communicate with larger power when the interference power threshold of the FCUs increases.Additionally, Fig.8 also verifies that the sum-rate of the V2V links increases with the number of the groups for the fixed number of the V2V links, and also increases with the number of the V2V links if the number of the groups is fixed.For example, whenImax=3×10-10mW andK=36, the sum-rate of the V2V links forN=5 is about 30 bit/Hz/s higher than that forN=4.

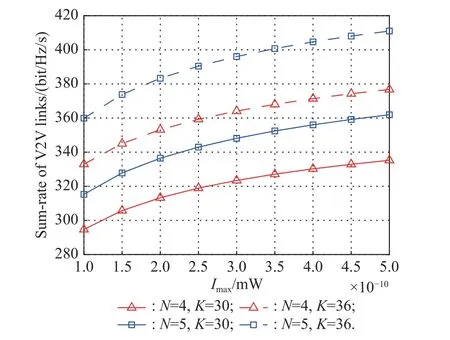
Fig.8 Sum-rate of V2V links versus the interference power threshold of FCUs, with v=100 km/h, and γ0=6 dB

In the case ofK=36,v=100 km/h, γ0=6 dB andImax=10-10mW, we compare the sum-rate of the proposed resource allocation scheme with the other two schemes, scheme A and scheme B in Fig.9.Scheme A adopts the random V2V partitioning policy and the same resource allocation as the proposed scheme, while scheme B utilizes the random RB assignment policy for the V2V links in each coalition and the same policy of V2V partitioning and power allocation as the proposed scheme.It shows that the proposed scheme obviously outperforms scheme A and scheme B.In addition, we find that the gap between the proposed scheme and scheme A first increases and then decreases.When the number of the V2V links in each group is large enough,both schemes cannot avoid strong interference of the V2V links.ForN=12, scheme A and scheme B have almost the same sum-rate of the V2V links.When the number of the V2V links at each group is small enough,the V2V links may have less mutual interference for both schemes.Therefore, it is indicated that selecting the appropriate number of the groups according to the number of the V2V links is particularly important to improve the performance of the V2V links.

Fig.10 demonstrates the impact of the vehicle speed onthe sum-rateofthe V2VlinksundertheconditionofK=30,N=4,andImax=10-10mW.In the simulation,the inter-vehicle distance increases as the vehicle speed increases.The channel gain of the V2V links decrease with the increase of the average inter-vehicle distance,therefore, the sum-rate of the V2V links decays as the vehicle speed increases.Furthermore, it is shown that the sum-rate of the V2V links decreases as the SINR threshold γ0grows from 6 dB to 18 dB.According to [1], for the fixed maximum interference powerImax, the transmit power of the FCUs increases with theincrease of γ0.Meanwhile, increasing the transmit power of the FCUs will enhance the interference from the FCU links to the V2V links.In another words, we can get higher sum-rate with smaller γ0.Moreover, if γ0becomes too large, we cannot find enough FCUs to share the RBs with the V2V link.However, γ0could not be too small considering the QoS of the FCU links.

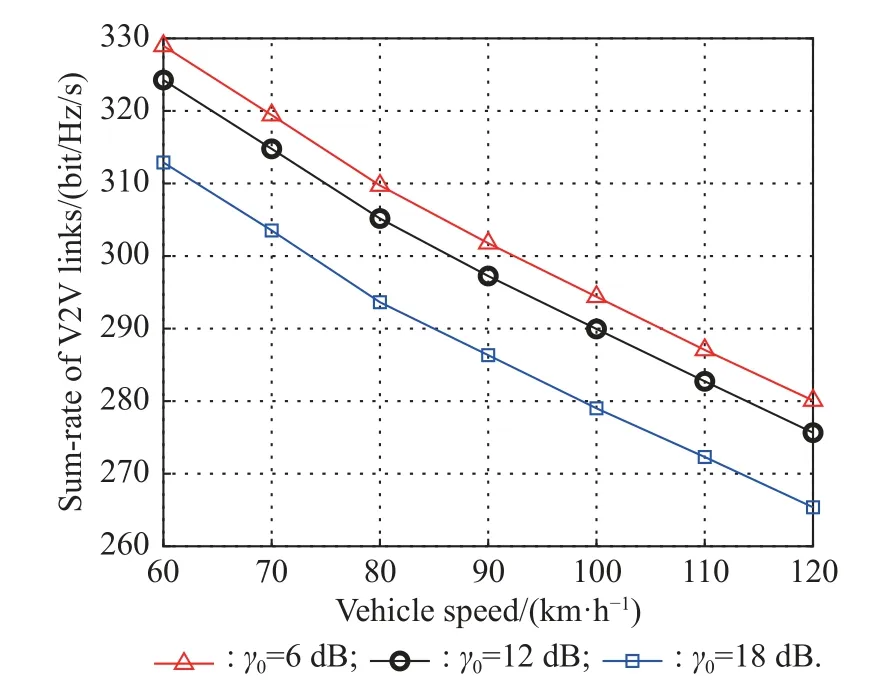
Fig.10 Sum-rate of V2V links versus the vehicle speed, with K=30, N=4, and Imax=10-10 mW

7.Conclusions

In this paper, to facilitate the interference management,we propose an optimization of the resource allocation in D2D-enabled V2V communication from the perspective of the V2V partitioning.Two coalition formation algorithms have been presented to divide the V2V link coalitions and select the appropriate FCU to share its RB for the V2V links in each group, respectively, which ensures the minimum mutual interference among the V2V links and the FCU uplinks.The power optimization problem is solved by SCA method and Lagrangian duality theory.Numerical results show that the proposed algorithm converges to the optimal solution through a finite number of iterations and achieve an obviously superior performance compared with the other random allocation schemes in terms of the sum-rate of the V2V links.