Multicriteria game approach to air-to-air combat tactical decisions for multiple UAVs
JIANG Ruhao, LUO He,3, MA Yingying, and WANG Guoqiang,3,*
1.School of Management, Hefei University of Technology, Hefei 230009, China;2.Key Laboratory of Process Optimization & Intelligent Decision-making, Ministry of Education, Hefei 230009, China;3.Intelligent Interconnected Systems Laboratory of Anhui Province, Hefei 230009, China
Abstract: Air-to-air combat tactical decisions for multiple unmanned aerial vehicles (ACTDMU) are a key decision-making step in beyond visual range combat.Complex influencing factors, strong antagonism and real-time requirements need to be considered in the ACTDMU problem.In this paper, we propose a multicriteria game approach to ACTDMU.This approach consists of a multicriteria game model and a Pareto Nash equilibrium algorithm.In this model, we form the strategy profiles for the integration of air-to-air combat tactics and weapon target assignment strategies by considering the correlation between them, and we design the vector payoff functions based on predominance factors.We propose a algorithm of Pareto Nash equilibrium based on preference relations using threshold constraints (PNE-PRTC), and we prove that the solutions obtained by this algorithm are refinements of Pareto Nash equilibrium solutions.The numerical experiments indicate that PNE-PRTC algorithm is considerably faster than the baseline algorithms and the performance is better.Especially on large-scale instances,the Pareto Nash equilibrium solutions can be calculated by PNEPRTC algorithm at the second level.The simulation experiments show that the multicriteria game approach is more effective than one-side decision approaches such as multiple-attribute decision-making and randomly chosen decisions.
Keywords: tactical decision, multicriteria game, preference relation, Pareto Nash equilibrium.
1.Introduction
With the improvement of unmanned aerial vehicle (UAV)detect ability and air-to-air missile performance, beyond visual range (BVR) combat has become an increasingly important research field in recent years [1,2].Many institutes, such as Defense Advanced Research Projects Agency (DARPA), Aeronautics Institute of Technology(ITA), are committed to studying the field [3-5].
This paper focuses on air-to-air combat tactical decisions for multiple UAVs (ACTDMU), which is a key step in BVR combat.The ACTDMU can be described as a decision-making problem, the purpose of which is to choose a reasonable tactic to ensure that UAVs complete the attack tasks safely and efficiently.Executing a reasonable tactic means occupying a dominant position.The analysis of the overall predominance value and the threat assessment of foe UAVs in the combat situation are the premises of this problem.Moreover, the ACTDMU problem is a macrolevel and complex decision-making process.This problem has characteristics such as complex influencing factors, an antagonistic combat environment,real-time requirements, and rapidly shifting predominance values [6].In particular, air-to-air combat tactical decisions and weapon target assignments (WTAs) are strongly correlated.Both decisions are key steps in air-toair combat situations, and both require UAVs to cooperate with each other to maximize the overall advantage over the foe’s UAVs.In addition, the time of decisionmaking for the two decisions overlaps, and the attack tasks for the two decisions are coupled with each other[7].These characteristics of the ACTDMU problem pose a challenge for its solution.
In recent years, many approaches to solving the ACTDMU problem have been proposed by researchers, and they are divided into two main categories: (i) Intelligent decision-making approaches based on theories such as multi-attribute decision-making (MADM) [8], rough sets[9], and fuzzy sets [10].In these approaches, the complexity of the influencing factors is considered, and tactics can be calculated rapidly by fuzzy reasoning.However, these approaches tend to make decisions from the perspective of one’s own side, and the impact of the decisions of others on one’s own side is ignored.It is difficult to describe the interaction between the selected strategies by using these approaches.(ii) The other decision-making approach is based on game theory [11,12].In this approach, the strong antagonism of air combat can be considered.The strategy profiles formed by all decision makers are analyzed first.Then, the payoffs for all sides with a single objective are obtained according to the characteristics of the problem.Finally, the solutions can be calculated by constructing a Nash equilibrium [13].Nevertheless, for this decision-making approach, it is difficult to fully represent the interaction relations between multiple influencing factors, which often leads to losing some useful information.The multicriteria game approach is an effective way to solve the ACTDMU problem.Not only the interaction relation among the complex influencing factors but also the interaction relation among all decision makers in choosing strategies is considered in this approach.
The multicriteria game was first proposed by Blackwell in 1956 [14].It is also termed a multiobjective game or vector payoff game.Multiple objectives or lists of payoffs are considered in this game, and this game has the ability to reflect multiple influencing factors.Unlike the classical Nash equilibrium, the Pareto Nash equilibrium(PNE) is usually constructed in the multicriteria game [15].Furthermore, various kinds of equilibria can be constructed by improving or refining the PNE according to the constraints of different multicriteria game problems.A large number of studies have focused on the definition of the equilibrium and proofs of the existence of its solutions.The Pareto-optimal security strategy equilibrium is constructed by using standard fuzzy orders to solve the multicriteria game problem with fuzzy payoffs [16].According to the attitude toward risk of the players in the games, the G-goal security strategy equilibrium is constructed to solve the multicriteria game problem with the desired goal [17].By considering the rational choice deviation of the decision makers, an ideal Nash equilibrium is constructed to refine the solution set of the PNE[18,19].The properly efficient Nash equilibrium is proposed to extend and perfect the efficient Nash equilibrium, and its sufficient existence conditions are established by using maximal elements [20,21].
PNE solutions play a central role in solving multicriteria games.Nevertheless, it is a recognized difficult problem to select compromise PNE solutions, which attempt to maximize all objectives, because this involves the construction of dominance relations and tedious calculations[22].For multicriteria games, there are few studies on easy-to-use PNE algorithms compared with the literature on the definition of equilibrium.Some studies attempt to calculate PNE solutions by linearly weighting the multicriteria game as a scalarized single-criterion game[23,24].However, the objectives of the decision makers are conflicting and coupled in many cases.It is difficult to calculate high-quality solution sets with a wide dispersion in this way.
In addition, combined with the concept of the PNE,other approaches for solving multicriteria games can be sorted into three categories.The first algorithm is based on optimization theory and transforms the multicriteria game problem into a linear programming problem, a quadratic programming problem or another problem[25-27].This kind of algorithm can find PNE solutions quickly, but it is usually suitable for biobjective games with small sizes.Second, artificial intelligence-based approaches are used to solve the multicriteria game.For example, the fuzzy set-based algorithm can calculate PNE solutions by constructing membership functions for fuzzy goals [28,29], and the heuristic algorithm can solve it by using a population evolution strategy [30,31].However, these algorithms are usually used in problems with low real-time requirements, and their application range is always limited for the problem constraints.The third type of algorithm is based on theories such as MADM and fuzzy decision-making, and it finds PNE solutions by establishing dominance relations [32,33].This approach is capable of solving non-zero-sum multicriteria game problems, and the construction of preference relations is a critical step that greatly affects the efficiency of the algorithm and the quality of the solutions.
In the ACTDMU problem, with the increase in the number of tactics and objectives, the degree of difficulty of solving it increases sharply [22].High-quality PNE solutions obtained with existing approaches always take a few seconds or even longer.It is difficult to meet the realtime requirements of this problem.Otherwise, combined with knowledge of air combat, it is necessary to build a model considering the characteristics of the ACTDMU problem.Thus, there is a gap in the usability of the approaches for solving the ACTDMU problem.In this paper, we propose a multicriteria game approach to the ACTDMU problem.This approach consists of a multicriteria game model and a PNE algorithm.The main highlights of this work are as follows:
(i) Strategy profiles for the integration of air-to-air combat tactics and WTA strategies are constructed by considering the correlation between them.
(ii) Vector payoff functions of multicriteria games are designed based on predominance factors considering the complexity of the influencing factors and strong antagonism in air-to-air combat.
(iii) A algorithm of PNE based on preference relations using threshold constraints (PNE-PRTC) is proposed.
(iv) The equilibrium solution obtained by the PNEPRTC algorithm is proven to be a refinement of the PNE solution.
The remainder of this paper is arranged as follows:Section 2 briefly describes the ACTDMU problem.In Section 3, a multicriteria game model for ACTDMU is established.The PNE-PRTC algorithm for solving the multicriteria game model is proposed in Section 4.Numerical experiments and simulation experiments are given in Section 5.Section 6 concludes the paper.
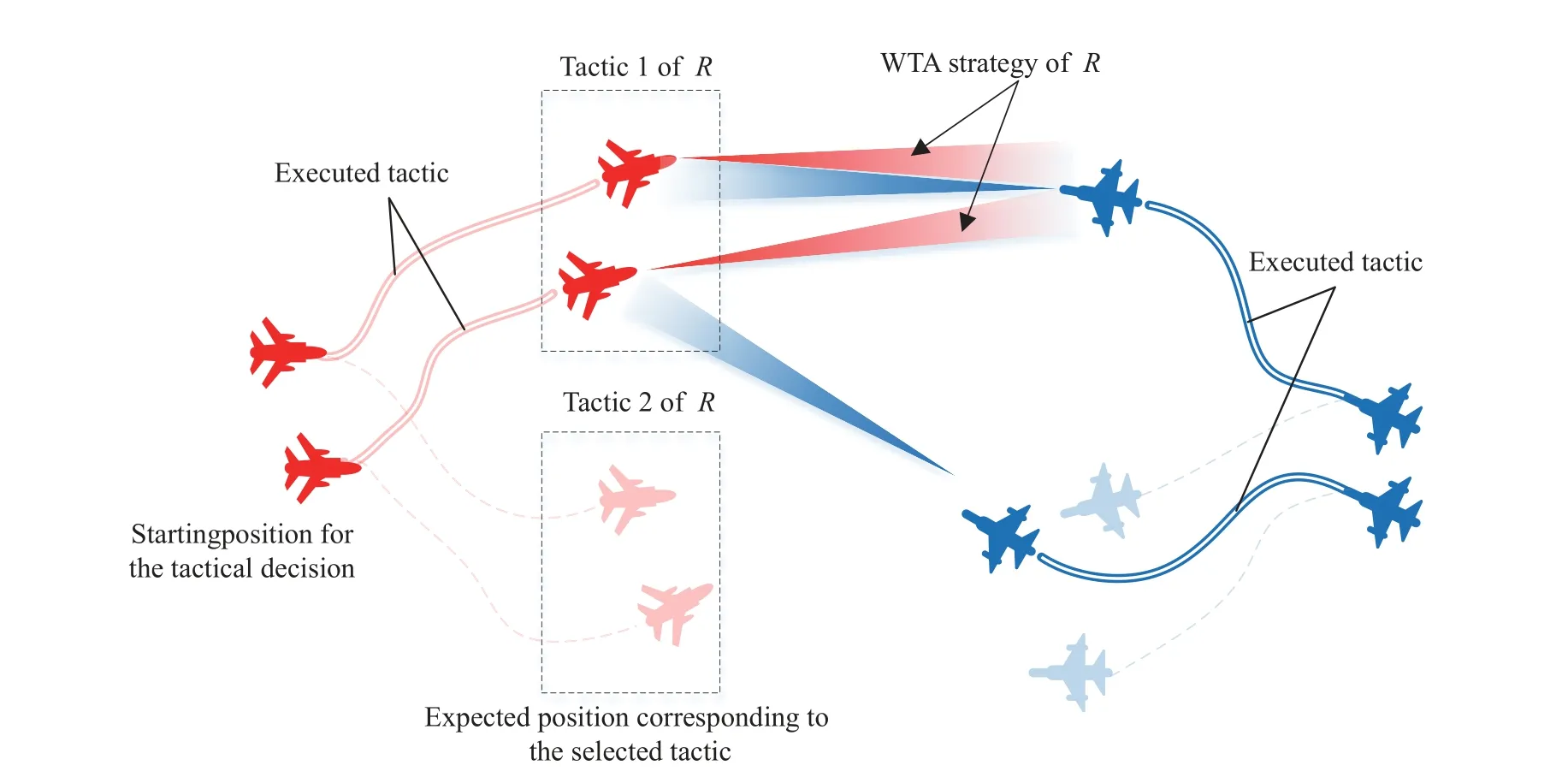
Fig.1 Executing the tactics in the ACTDMU problem
2.Problem formulation
ACTDMU is a macroscopic decision-making problem in beyond-visual-range combat.First, it is necessary to fully analyze the predominance value in a combat situation and evaluate the threat levels of foe UAVs.Then, tactics affected by multiple-decision information are compared and selected according to superiority.Finally, a reasonable tactic is executed to maximize the overall advantage of our UAV swarm against the foe’s targets.The characteristics of the ACTDMU problem require that decisions be made as quickly as possible.Fig.1 shows that a selected tactic is executed in the ACTDMU problem.

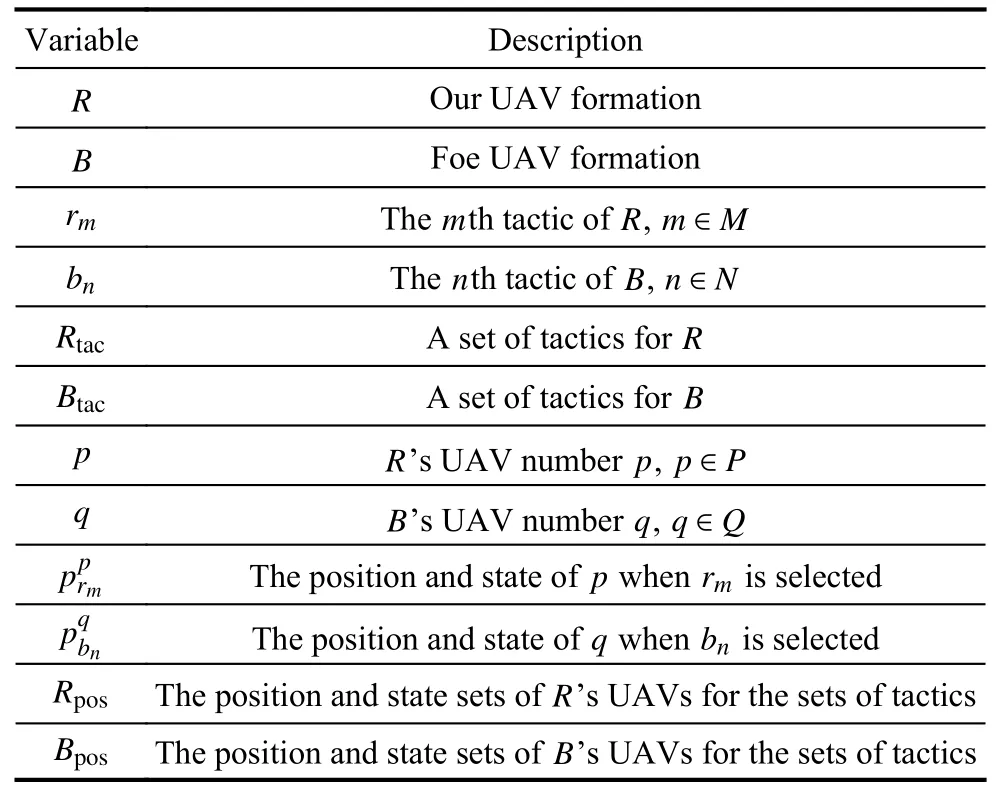
Table 1 Parameter definitions of the ACTDMU problem
3.Multicriteria game model

3.1 Strategy profiles
First, the sets of air-to-air combat tactics incorporating the WTA strategies ofRandBare constructed, and then the set of strategy profiles for integrating air-to-air combat tactics and WTA strategies are formed.
(i) Sets of air-to-air combat tactics incorporating WTA strategies

3.2 Vector payoff functions
In the ACTDMU problem, the vector payoff functions consist of two sets of objective functions according to the validity of the fighting effect and the threat assessment of foe UAVs.The two sets of objective functions are constructed by using four predominance factors: speed predominance, angle predominance, altitude predominance,and distance predominance.Each objective function in a set is constructed by using one predominance factor.For example, for speed predominance,R’s objective function of the validity of the fighting effect is denoted asfR1.For angle predominance, altitude predominance and distance predominance,R’s objective functions of the validity of the fighting effect are denoted asfR2,fR3andfR4, respectively.Similarly,R’s objective functions of the threat assessment of the foe UAVs in terms of speed predominance, angle predominance, altitude predominance and distance predominance are denoted asfR5,fR6,fR7andfR8, respectively.R’ s vector payoff functionFR=(fR1,fR2,···,fR8)tis composed of eight objective functions.Similar to that ofR,B’s vector payoff functionFB=(fB1,fB2,···,fB8)tis constructed.
Thejth objective function ofiis expressed as



For the set of strategy profiles for integrating air-to-air combat tactics and WTA strategies, the vector payoff functions ofRandBfor every objective are constructed.Then, the vector payoff matrices shown in (4) and (5) can be calculated.
4.Algorithm design
It is necessary to study an algorithm to obtain the highquality PNE solutions at a fast speed because of the ACTDMU problem’s real-time requirements.The general framework of the PNE-PRTC algorithm for the multicriteria game model is introduced in Subsection 4.1.Subsection 4.2 proves that the solution obtained by the PNEPRTC algorithm is a refinement of the PNE solution.
4.1 PNE-PRTC algorithm
There are conflicts, coupling and incommensurability among the multiple objectives of the multicriteria game model.It is difficult to accurately obtain the opponent’s objective weight.To solve the multicriteria game model,the PNE-PRTC is proposed in this paper.This algorithm is inspired by the PNE algorithm proposed in [32], and it can solve the PNE without weights.The preference relations are redefined in the PNE-PRTC algorithm.Furthermore, weak partial binary relation constraints and negative threshold constraints are added to construct a fivelevel domination criterion.A decisive step toward the optimal solution is provided for the PNE solution sets.The general framework of the PNE-PRTC algorithm is shown in Fig.2.
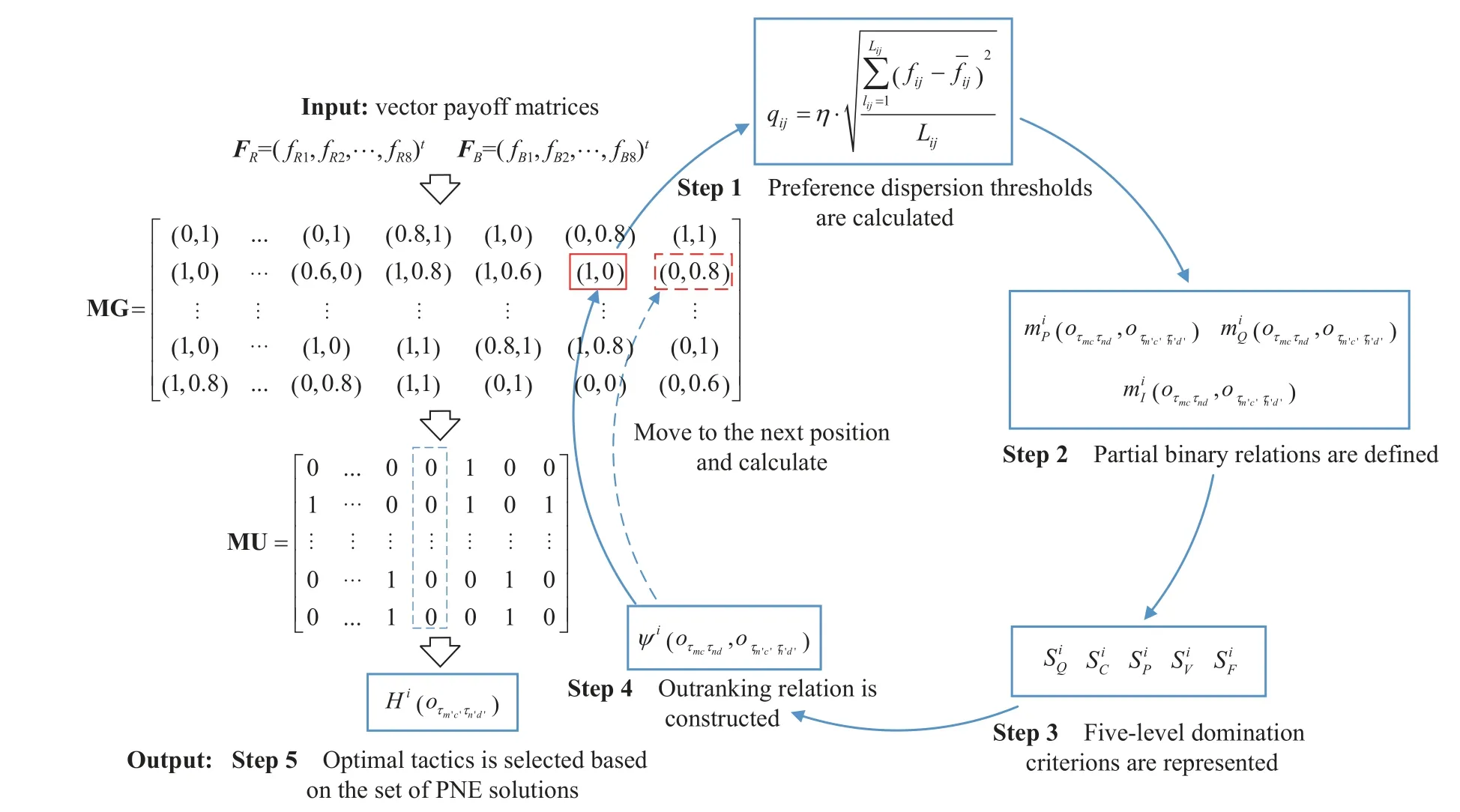
Fig.2 General framework of the PNE-PRTC algorithm
First, the preference dispersion thresholds are calculated by extracting the discrete characteristics of the vector payoff matrices.Second, the partial binary relations are defined.Then, a five-level domination criterion is presented according to the combination of partial binary relations.Next, the outranking relation is constructed by the level of preferences restricted to the domination criterion, and the preference relations, as outranking relations corresponding to all strategy profiles, are represented by the values 0, 1, etc.Finally, the set of equilibrium solutions that are solved according to the strategies of each player are the best responses, and the optimal tactics are selected by a decision rule.The key steps in the PNEPRTC algorithm are designed as follows:
Step 1 The preference dispersion thresholds are calculated by
whereXijrepresents the number of samples selected for thejth objective function ofi,i=R,B.η is defined as the threshold scaling coefficient, which ranges from 0.5 to 1.5.By multiplying the standard deviation with the threshold scaling coefficient, the dispersion degree characteristic of the vector payoff matrices is extracted as the preference dispersion threshold, which is used to measurei’s sensitivity of the degree of outranking the vector payoffs in each objective.


Table 2 Partial binary relations of noncooperative situations
Step 3 To establish an outranking relation, a fivelevel domination criterion is constructed.


In (8), a matrix of global information MG, which is composed of the values 0, 0.2, 0.4, 0.6, 0.8, and 1, is formed by gathering all the outranking relations corresponding to the links between every pair of strategy profiles.Then, a matrix of useful information MU, which consists of refined outranking relations, is constructed to extract the noncooperative equilibrium (NCE) solution by(9), according to the formula for searching for NCE solutions in [32].

In summary, Step 1 to Step 4 demonstrate the process of the PNE-PRTC algorithm.The role of Step 5 is to make the final decision from the PNE solution sets, and this step can also be flexibly replaced by other decision approaches based on the decision maker’s preferences.
4.2 Proof of the PNE solution
The equilibrium solutions obtained by the PNE-PRTC algorithm are the NCE solutions in Subsection 4.1.In this section, we need to prove that the NCE solutions are refinements of the PNE solution.First, the definitions involved are summarized [32,40].
Definition 6Fora,b∈Rn, the notation of vector inequalities is defined as follows:

5.Experiments
To verify the generality and efficiency of the PNE-PRTC algorithm, numerical experiments are carried out in Subsection 5.1.Simulation experiments are analyzed in Subsection 5.2 to verify the effectiveness and correctness of the multicriteria game model.All experiments are run on computers with an Intel i7-7700 3.60 GHz CPU and 32 GB RAM.
5.1 Numerical experiments
The parametric analysis of the PNE-PRTC algorithm is performed first.Then, the performance metrics of the PNE-PRTC algorithm considering the optimal parameters are employed.Three different datasets represented by Set 1, Set 2, and Set 3 are generated by the leading game generator GAMUT [41].Each dataset includes 15 different sizes of instances, and each size includes 20 instances of a multicriteria game, as shown in Table 3.The vector-valued payoffs for the multicriteria games range from 0 to 1.α×β×χ represents multicriteria games with the same size.α and β denote the numbers ofR’s strategies andB’s strategies.χ represents the objective number for each side.
5.1.1 Performance metrics
Unlike matrix games, which evaluate the quality of Nash equilibrium solutions by comparing payoffs with the same dimension, it is difficult to measure the quality of the solutions with a single performance metric for multicriteria games because of payoffs that are vector valued.Similar to the performance metrics of multiobjective optimization, in this paper, the quality of PNE solutions is measured in three respects: convergence, uniformity and spread.The performance metrics of the multicriteria game are described as shown in (13), (14), and (15).
Definition 10 Average hypervolume for a multicriteria game [42] can be expressed as
whereSsetdenotes vector payoff matrices with the same size,Sset=20.NPNErepresents the PNE solution set obtained by the PNE-PRTC algorithm, andnPNEis a PNE solution,nPNE∈NPNE.pPNEdenotes a reference point.hv indicates the hypervolume value enclosed byNPNEandpPNE.The quality of the PNE solution set in terms of the convergence and diversity of the vector payoffs is evaluated in (13).A larger value ofWHVmeans that the PNE solution sets are more convergent and diverse.
Definition 11 Average spacing metric for the multicriteria game [43] can be expressed as
Definition 12 Average diversity measure for the multicriteria game [44] can be expressed as
WDis used to measure the diagonal length of the hypercube formed by the extreme objective values in a PNE solution set.It is a basic indicator that can reflect the diversity of a PNE solution set.Clearly, the higher the value ofWDis, the better the distribution of the PNE solution set.
5.1.2 Parametric analysis
The threshold scaling coefficient η is a key parameter that strongly affects the performance of the PNE-PRTC algorithm, and parametric analyses must be carried out to optimize its performance.We change η from 0.5 to 1.5 with a step size of 0.1.A total of 9 900 parametric analyses are conducted, with 20 multicriteria games conducted for each η in different sizes of instances.The quality of the PNE solution set is evaluated by three metrics: the average hypervolumeWHV, average spacing metricWSPand average diversity measureWD.Fig.3 shows the results of numerical experiments for the PNE-PRTC algorithm with different η.Specifically, Fig.3 (a), Fig.3 (b),and Fig.3 (c) represent the evaluation ofR’s vector payoffs corresponding to the PNE solutions for Set 1.Similarly, Fig.3(d), Fig.3(e), Fig.3(f) and Fig.3(g),Fig.3(h), Fig.3(i) represent the evaluation ofR’s vector payoffs corresponding to the PNE solutions for Set 2 and Set 3, respectively.
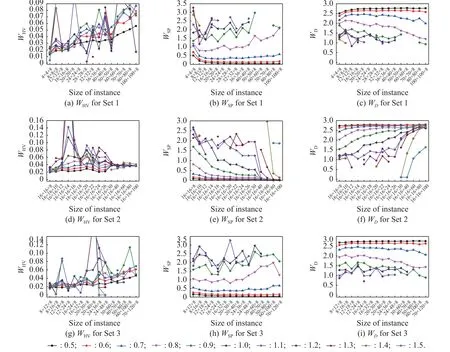
Fig.3 Comparison of the results of numerical experiments for the PNE-PRTC algorithm with different η
Generally, in all subplots of Fig.3, as the η value increases, theWHVandWSPvalues for multicriteria games obtained by using the PNE-PRTC algorithm gradually increase, whileWDgradually decreases.There is a certain positive correlation between the optimal value of theWSPcurve and theWDcurve.Nevertheless, there is a certain negative correlation between the optimal value of theWHVcurve and theWSPcurve.The correlation among the three performance metrics makes it difficult to achieve the optimal value for the metrics at the same time by adjusting η , but η can be adjusted to a compromise value according to the decision maker’s preference on different performance metrics.In addition, when the value of η is greater than 0.9, as η increases, the variation ranges ofWHV,WSPandWDare significant.This finding implies that the larger the value of η, the greater the preference dispersion thresholdqij, the more difficult it is to construct a binary relationSi, and the smaller the number of PNE solutions calculated by the PNE-PRTC algorithm.When the number of PNE solutions drops to 0,WHVsuddenly falls to 0, andWSPandWDcannot be calculated, leading to unstable solution results.This eventually leads to the fluctuation and fracture of the curve.
For three different datasets, the performance metrics of the PNE-PRTC algorithm are analyzed in detail as follows:
(i) TheWHVcurves corresponding to the datasets are shown in Fig.3 (a), Fig.3 (d), and Fig.3 (g).When η is fixed,WHVfor Set 1 and Set 3 increases significantly as the number of strategies increases, whileWHVfor Set 2 does not grow sharply with the increase in the number of objectives.The reason is that as the number of strategies increases, the strategy profiles increase significantly, the number of partial binary relations in Step 2 of the PNEPRTC algorithm rises sharply, and the PNE solution sets obtained by the algorithm become larger.This makes it easier for the algorithm to balance the convergence and diversity of the PNE solution sets.The increase in the objectives does not increase the strategy profiles but increases the complexity of constructing preference relations for all strategy profiles.In addition, with the increase in the objects of instances in Set 2, the fluctuation range of theWHVvalue of the PNE-PRTC algorithm gradually decreases, especially for large-scale instances.The reason for this is that the PNE solution sets calculated by the PNE-PRTC algorithm are larger and more uniform for solving large-scale instances.
(ii) TheWSPcurves corresponding to the datasets are shown in Fig.3 (b), Fig.3 (e) and Fig.3 (h).Similarly,theWDcurves are shown in Fig.3 (c), Fig.3 (f) and Fig.3 (i).When η is fixed, compared with Set 1 and Set 3,as the number of objectives in Set 2 increases, the trend of decreasingWSPand increasingWDbecomes more obvious, especially when solving the large-scale instances.The reason is that as the number of objectives increases, it becomes more difficult to construct binary relations for each pair of vector payoffs by using the PNEPRTC algorithm, the PNE solutions become more harmonious across vector payoffs, and the distribution of PNE solutions becomes more uniform and diverse.
Considering the positive and negative correlations among theWHV,WSPandWDcurves in Fig.3, the η values of the PNE-PRTC algorithm for different datasets are shown in Table 3.
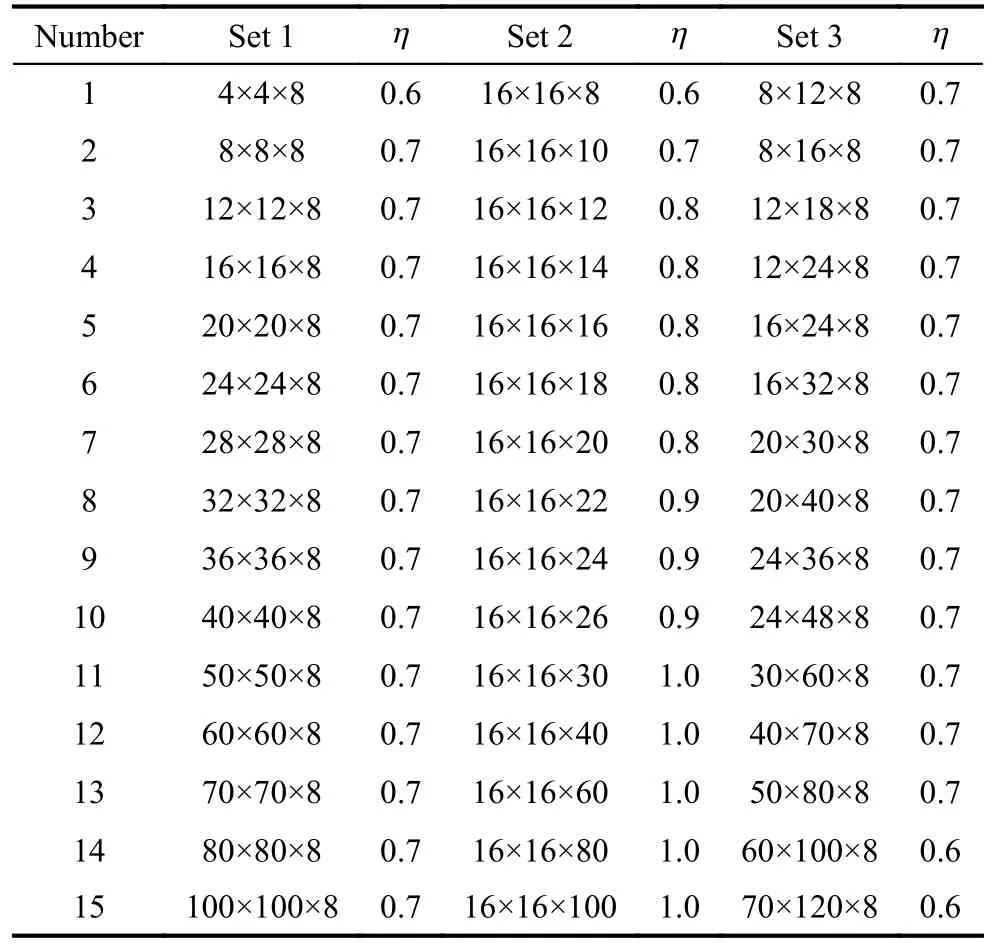
Table 3 Threshold scaling coefficient settings of the PNE-PRTC algorithm for different datasets
5.1.3 Comparison experiments
In this subsection, the proposed algorithm is compared with the algorithm of PNE based on the preference relation (PNE-E, PNE-P) proposed in [32] and the algorithm of PNE based on the scalarized single criterion (PNE-S)presented in [24].The weights of the PNE-E, PNE-P, and PNE-S algorithms are set to the same value according to the principle of maximum entropy [45].A total of 45 sizes of instances are solved on three datasets.For each size of instance, 20 multicriteria game instances are solved when the value is chosen according to Table 3.The average computational times (ACTs) of the PNE-S,PNE-E, PNE-P, and PNE-PRTC algorithms are shown in Fig.4.Three performancemetrics,WHV,WSPandWD, of thesealgorithmsareshownin Fig.5.
From the overall trends shown in Fig.4, it is clear that the ACT of the PNE-PRTC algorithm is less than those of the PNE-E and PNE-P algorithms, and the ACT curves of the PNE-PRTC and PNE-S algorithms almost overlap.To solve the large-scale instances, the solution time of PNEE and PNE-P algorithms increases exponentially with increasing instance size.When the size of instances in Set 1 is greater than 60×60×8, or the size of instances in Set 3 is greater than 50×80×8, the PNE solution sets cannot be calculated within six hours by using the above baseline algorithms.However, the effective PNE solution sets of the large-scale instances can be solved stably by the PNEPRTC and PNE-E algorithms within seconds.
The reason for this is that it is necessary for the PNE-E and PNE-P algorithms to calculate the deviation distance for every objective and sort them when constructing the binary relation for a pair of strategy profiles.The original sorting needs to be updated for each binary relation.This repetitive sorting can cost much time.For the PNE-PRTC algorithm, the binary relations are constructed by the preference dispersion thresholds, which can reflect the discrete characteristics of the vector payoffs for each objective function.Repetitive sorting steps are not needed.Although the PNE-E, PNE-P, and PNE-PRTC algorithms can all solve multicriteria games based on preference relations, the PNE-PRTC algorithm can be even more efficient than the PNE-E and PNE-P algorithms.
The ACT of the PNE-PRTC algorithm on the three datasets is analyzed as follows: In Fig.4 (a) and Fig.4 (c),the ACT on Set 1 and Set 3 gradually increases as the number of strategies increases, while the ACT on Set 2 increases slightly as the number of objectives increases in Fig.4 (b).The reason is that as the number of strategies increases in Set 1 and Set 3, the search space of the PNE solutions rises rapidly.For Set 2, as the number of objectives increases, the search space of PNE solutions does not change, but it is more difficult to construct preference relations for the strategy profiles.The slight increase in the ACT on Set 2 illustrates that the PNEPRTC algorithm is able to construct binary relations efficiently for a pair of strategy profiles even in high-dimensional objectives.The ACT of the PNE-PRTC algorithm is more sensitive to the increase in the number of strategies than the number of objectives at the sizes selected in this paper.
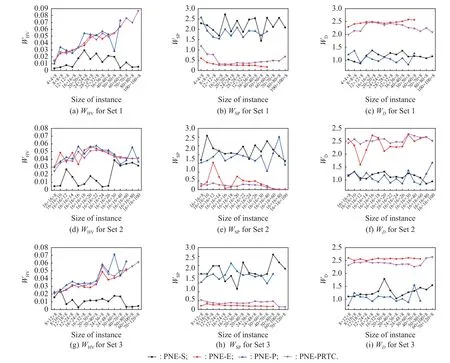
Fig.5 Comparison of the results of the performance experiments for the PNE-S, PNE-E, PNE-P, and PNE-PRTC algorithms
Generally, in Fig.5 (a), Fig.5 (d), and Fig.5 (g), theWHVcurves of the PNE-E, PNE-P, and PNE-PRTC algorithms are almost higher than the curves of the PNE-S algorithm.In Fig.5 (b), Fig.5(e), Fig.5(h) and Fig.5 (c),Fig.5(f), Fig.5(i), the overall trends of theWSPandWDcurves of the PNE-S and PNE-P algorithms are roughly the same.In all subplots of Fig.5, theWHV,WSPandWDcurves of the PNE-E and PNE-PRTC algorithms have similar trends and even overlap with each other.To solve the large-scale instances, high-quality PNE solution sets can be calculated stably by the PNE-PRTC algorithm.We can conclude that the performances of the PNE-PRTC algorithm and PNE-E algorithm are very close, and the PNE-PRTC algorithm outperforms the PNE-S algorithm in all three metricsWHV,WSP, andWD.
For the instances that can be solved by the baseline algorithms, the three performance metricsWHV,WSP, andWDof the PNE-E, PNE-P, and PNE-PRTC algorithms are analyzed in detail below.
(i) For the performance metricWHVshown in Fig.5 (a),Fig.5(d) and Fig.5(g), theWHVof the PNE-PRTC algorithm improves by 319.9% on average compared with that of the PNE-S algorithm and by 5.6% on average compared with that of the PNE-E algorithm, and it is slightly lower than that of the PNE-P algorithm.However, the variation ranges ofWHVfor the PNE-PRTC algorithm are narrower than those for the PNE-P algorithm, which indicates that the PNE-PRTC algorithm is more stable.
(ii) For the performance metricWSPshown in Fig.5 (b),Fig.5(e) and Fig.5(h), with different sizes of instances,theWSPof the PNE-PRTC algorithm decreases by 82.1%on average compared with that of the PNE-S algorithm and by 79.8% on average compared with that of the PNEP algorithm.TheWSPcurves for the PNE-PRTC algorithm are smoother than the other curves, indicating that the PNE-PRTC algorithm has a more uniform distribution of PNE solution sets than the PNE-S algorithm and the PNE-P algorithm.
(iii) For the performance metricWDshown in Fig.5 (c),Fig.5(f), Fig.5(i), theWDof the PNE-PRTC algorithm improves by 106.4% on average compared with that of the PNE-S algorithm and by 129.7% on average compared with that of the PNE-P algorithm.The small variation ranges ofWDfor the PNE-PRTC algorithm indicate that the PNE solution sets obtained by the PNE-PRTC algorithm are diverse.
5.2 Simulation experiments
A multiple-UAV cooperative confrontation simulation system is constructed based on VR-Forces, which is distributed computer force generation software.In this simulation system, red and blue UAV entities can be constructed, and flight, missile launch and damage can be simulated for these UAVs.Fig.6 shows typical two-ontwo air combat tactical decision scenarios designed in this simulation system.The red and blue roles, involving multiple UAVs, and the white role, with a global perspective,are established.This deployment can be used to simulate air-to-air combat tactical decisions.The multicriteria game approach of ACTDMU (MG-ACTDMU), composed of a multicriteria game model and the PNE-PRTC algorithm, is programmed in the Visual C++ language.The software plugin used to load this approach is developed for embedding in this simulation system.The simulation data in air combat tactical decision scenarios can be obtained by the data logger function in VR-Forces.MySQL workbench software is used to extract simulation information such as the UAV position and state, missile launches and other information by setting time stamp constraints.
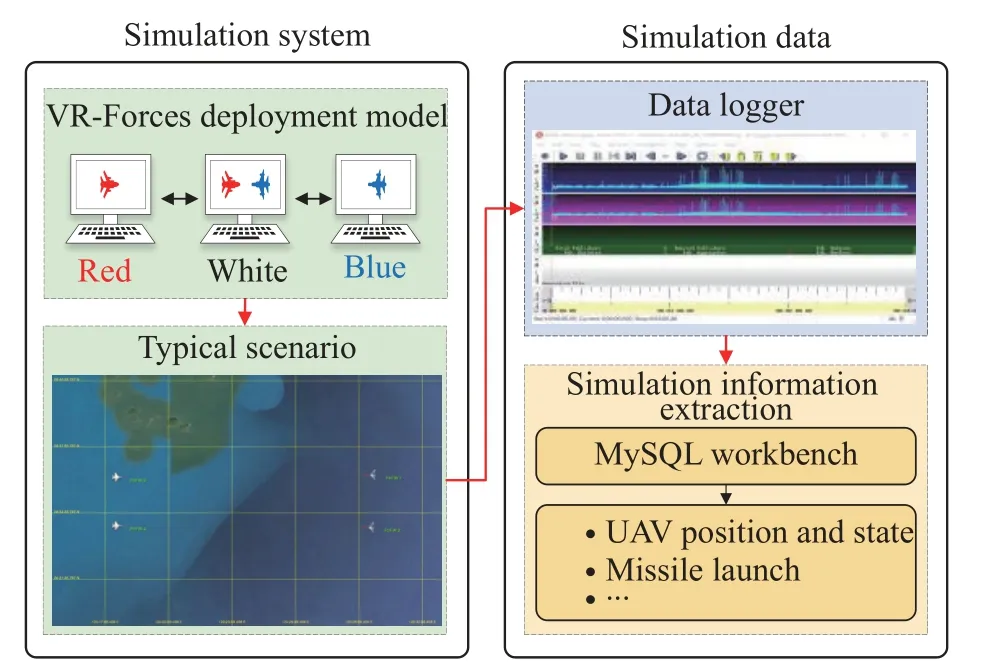
Fig.6 Deployment mode and process of obtaining simulation information
5.2.1 Simulation scenarios
In a multiple-UAV cooperative confrontation simulation system, three simulation scenarios are designed according to the foe’s tactical styles: offensive, neutral, and defensive.The possible tactics chosen forBare shown in Table 4.Ris able to choose one of five tactics, including the Head-on Bracket tactic (a), the Turn-away Drag tactic (b), Loose Deuce Engagement tactic (c), Tac-Turn Disengagement tatic (d), and Defensive split tactic (e) [46].
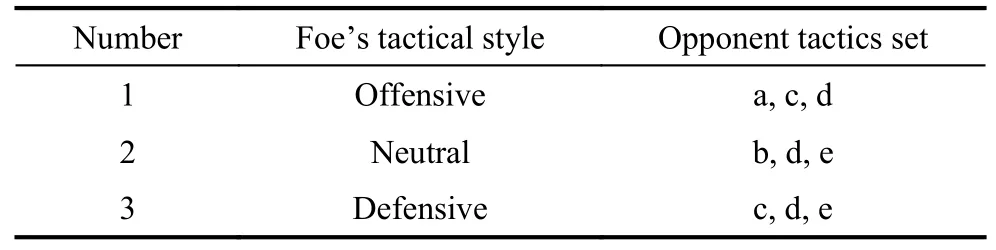
Table 4 Three foe tactical style settings
B, as the baseline opponent, selects the best responses strategies toR’s strategy.Rselects the strategies based on the calculation results of the different approaches.The vector payoffs ofRare compared in this simulation.We introduce two typical decision-making approaches and compare them with the MG-ACTDMU approach proposed in this paper.The detailed settings of the three approaches are as follows:
(i) MG-ACTDMU:Rselects the tactics corresponding to the PNE solutions obtained by MG-ACTDMU.
(ii) MADM:Rselects the tactics corresponding to the optimal solutions obtained by MADM.
(iii) Random:Rselects tactics randomly based on uniformly distributed sampling.
5.2.2 Evaluation metrics
Three evaluation metrics are employed for the simulation experiments.
Definition 13 Hypervolume ofR.The average hypervolume, given in Definition 10, is used to evaluate the quality of the vector payoffs corresponding to the selected tactic.Since only one tactic is selected for each simulation, Definition 10 is simplified to
wherenPNEdenotes a PNE solution.pPNEdenotes a reference point.hv indicates the hypervolume enclosed bynPNE andpPNE.
Definition 14 Winning percentage ofR[47].After a simulation, if the number of surviving UAVs ofRis greater than that ofB, thenRwins.The winning percentage is calculated by
wherenwinrepresents the number of wins ofRandnallis the total number of simulation experiments.
Definition 15 Kill ratio ofR[48].The kill ratio is calculated by
whereLRrepresentstheamount of damagetoR’sUAVs andLBrepresentsthe amount of damage toB’sUAVsin all simulation experiments.Clearly, the smaller the kill ratio is, the greater the advantage ofRin the simulation experiments.
5.2.3 Simulation results
In this section, a case study is first analyzed to illustrate the rationality and stability of the solution obtained by the MG-ACTDMU approach.Then, the effectiveness and efficiency of the approach proposed in this paper is verified by simulation comparison experiments.
(i) Case study


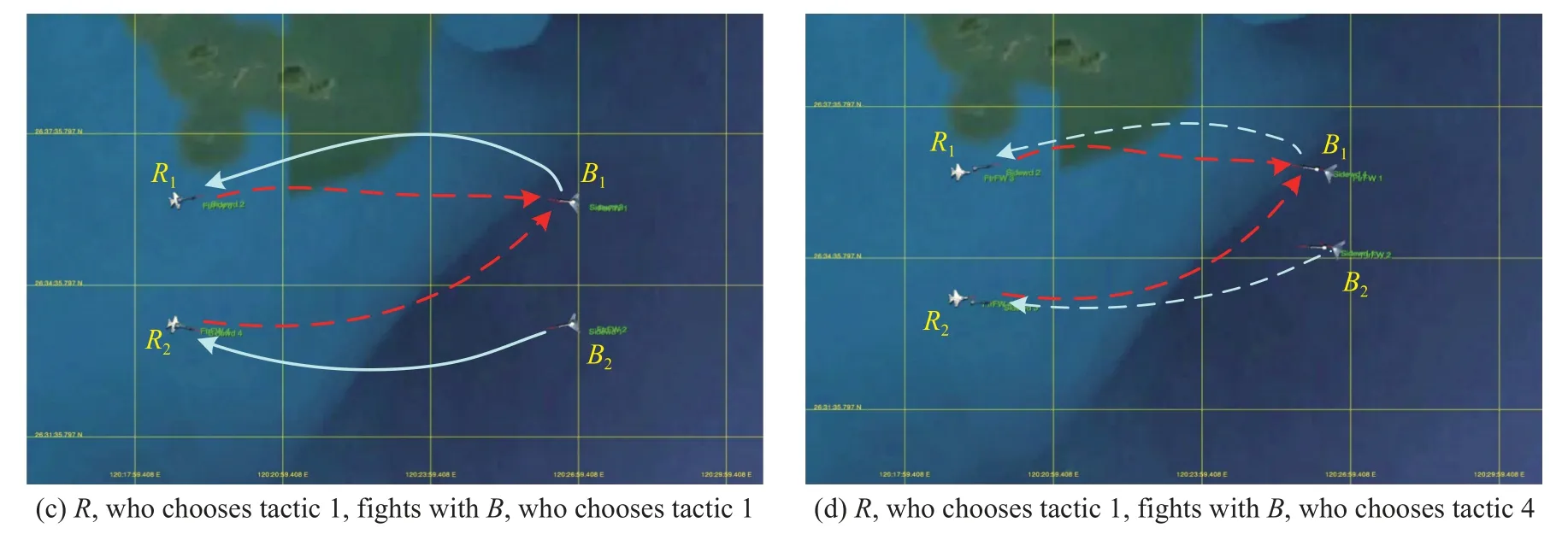
Fig.7 Executions of tactics corresponding to PNE solutions and non-PNE solutions
Table 5 shows the UAV position and state whenRchoosesrr2w2,rr1w2andBchoosesbb1v1,bb4v1.Table 6 indicates the vector payoff matrices calculated by using the MG-ACTDMU approach and the corresponding executions of tactics for the selected strategy profiles.Parameters and vector payoffs associated with PNE are marked in bold.

Table 5 UAV position and state corresponding to the selected tactics
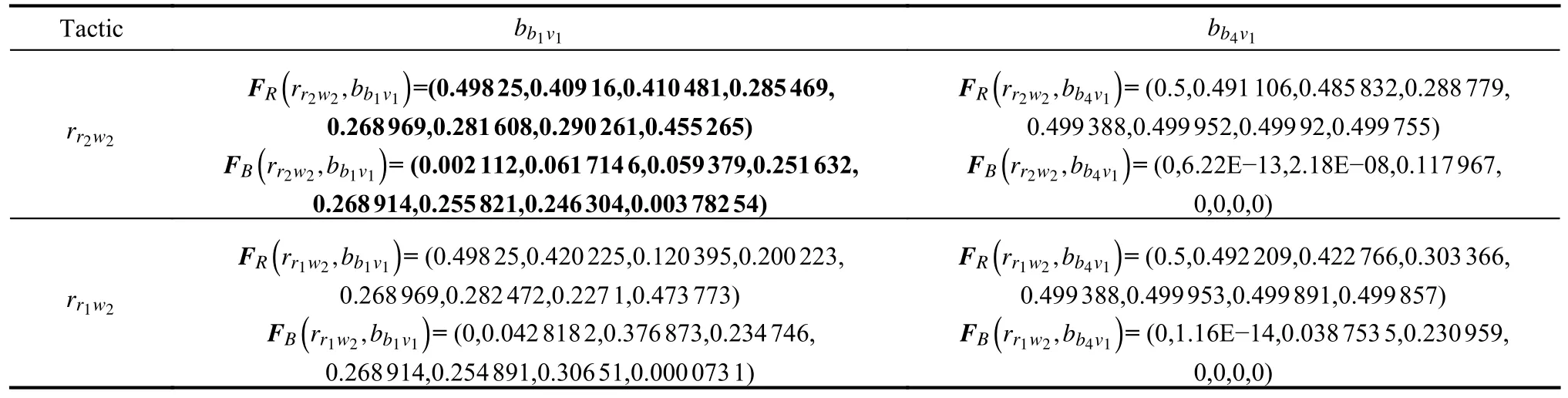
Table 6 Vector payoff matrices and corresponding executions of tactics for the selected strategy profiles


(ii) Simulation results
Three scenarios are designed according toB’s three tactical styles.In each scenario, the MG-ACTDMU approach, MADM approach and random approach are used to solve the ACTDMU problem forR, and 100 simulation experiments are carried out for each approach.The three evaluation metrics in Subsection 5.2.2 are calculated based on the simulation information obtained from the data logger function in VR-Forces.The three evaluation metrics for the MG-ACTDMU, MADM and random approaches are shown in Table 7 where the results of our MG-ACTDMU are marked in bold.
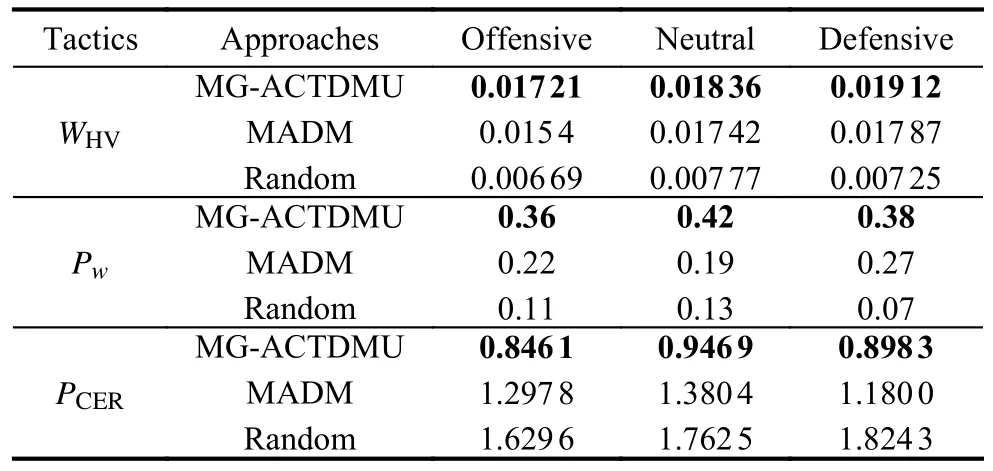
Table 7 Three evaluation metrics for the MG-ACTDMU, MADM and random approaches
The simulation results show that the MG-ACTDMU approach proposed in this paper is obviously better than the MADM approach and random approach for the above three scenarios.
Compared with the MADM approach, the hypervolumeWHVof the MG-ACTDMU approach is greater, the winning percentagePwis increased by 70.6% on average and the kill ratioPCERis decreased by 30.2% on average.Compared with the random approach, theWHVof the MGACTDMU approach is significantly greater,Pwis increased by 274.2% on average andPCERis decreased by 48.0% on average.The simulation analysis shows that the MG-ACTDMU approach can effectively improve the winning percentage and reduce the kill ratio of UAVs.The reason is that the optimal strategy forRis selected by the MG-ACTDMU approach when the most favorable situation forBis reached.However, the MADM approach and random approach only make decisions from their own perspective, and ignoring the impact of the opponent’s decision on our decision leads to a failure to achieve the desired results.
6.Conclusions
In the process of beyond-visual-range combat, ACTDMU is a key step.This study proposes a MG-ACTDMU.Our approach includes a multicriteria game model and a PNEPRTC.For the model, sets of air-to-air combat tactics incorporating WTA strategies are constructed.In addition, the vector payoff functions of the multicriteria game are designed based on four predominance factors.For the algorithm, weak partial binary relation constraints and negative threshold constraints are added to construct a five-level domination criterion.Then, the preference relations are redefined.It is proven that the solutions of the PNE-PRTC algorithm are refinements of PNE solutions.
A leading game generator, GAMUT, is used to generate three datasets with 45 sizes of instances.These datasets can provide a benchmark for research in the field of multicriteria games.The numerical experiments show that the PNE-PRTC algorithm has a high speed, and its performance is better in terms of the average spacing metric and average diversity measure than the baseline algorithms.In particular, the PNE-PRTC algorithm has more advantages for solving large-scale instances.This algorithm can be applied not only to the ACTDMU problem in this paper but also to general multicriteria games.
A multiple-UAV cooperative air combat simulation system is constructed based on VR-Forces software.This simulation system lays the foundation for testing the effect of this approach and the development of future works.The simulation experiments show that the MGACTDMU approach is more effective than the multipleattribute decision-making approach and the randomly chosen decision approach for solving the ACTDMU problem.A case study is used to analyze the stability and effectiveness of the solutions obtained by this approach.
In future work, uncertainty regarding the capability of foe UAVs should be taken into account in the ACTDMU problem.In addition, improving the robustness of the multicriteria game algorithm and refining the PNE solution sets are important research directions.
 Journal of Systems Engineering and Electronics2023年6期
Journal of Systems Engineering and Electronics2023年6期
- Journal of Systems Engineering and Electronics的其它文章
- Two-layer formation-containment fault-tolerant control of fixed-wing UAV swarm for dynamic target tracking
- Role-based Bayesian decision framework for autonomous unmanned systems
- Nonlinear direct data-driven control for UAV formation flight system
- Minimum-energy leader-following formation of distributed multiagent systems with communication constraints
- A survey on joint-operation application for unmanned swarm formations under a complex confrontation environment
- A consensus time synchronization protocol in wireless sensor network
