Vegetation scattering attenuation characteristics of terahertz wave

JING Qingfeng, DIAO Zhuo, and ZHU Zhongbo

1.College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210019, China;2.The 28th Research Institute of China Electronics Technology Group Corporation, Nanjing 210000, China;3.The 504 Research Institution, China Aerospace Science and Technology Corporation, Xi’an 710100, China

Abstract: A terahertz (THz) wave transmitted through vegetation experiences both absorption and scattering caused by the air molecules and leaves.This paper presents the scattering attenuation characteristics of vegetation in a THz range.The theoretical path loss model near the vegetation yields the average attenuation of THz waves in a mixed channel composed of air and vegetation leaves.Furthermore, a simplified model of the vegetation structure is obtained for generic vegetation types based on a variety of parameters, such as leaf size, distribution,and moisture content.Finally, based on specific vegetation species and different levels of air humidity, the attenuation characteristics under different conditions are calculated, and the influence of different model parameters on the attenuation characteristics is obtained.

Keywords: terahertz (THz), scatter attenuation, vegetation, vegetation structure model.

1.Introduction

Terahertz (THz) technology has become a hotspot of research due to its application prospects.THz has a wide range of applications, such as atmospheric communication [1,2], material detection [3,4], and medical imaging[5,6].Only a few studies focused on the scattering characteristics of the THz waves reflected by and transmitted through a plant leaf under different water contents to obtain plant water content and monitor plant health[7-10].Torres et al.[11] conducted THz transmission experiments on living leaves of several common edible plants.In addition, based on the time-domain finite integral technique (TDFIT), Li et al.[12] analyzed the transmission characteristics of leaves with different humidity in the THz band, and compared the transmission characteristics of dry leaves and wet leaves under THz irradiation.Six scenario modules for milimeter (mm) waves and THz train-to-infrastructure channels were defined and constructed by Ke et al.[13], with the vegetation being one of the main objects considered in the modules.Zahid et al.[14] observed the effects of blade thickness and water contents on transmission loss and attenuation in different frequency regions using THz system.Afsharinejad et al.[15] proposed that a wireless nano sensor network can be used for accurate agricultural monitoring from the perspective of THz communication.

There are a few studies on the attenuation of THz waves in vegetation, mainly because such research requires a large amount of experimental measurement data.When the THz wave passes through the vegetation during the transmission, it is affected by the absorption of air molecules and leaves, as well as the scattering effect of the leaves.Some existing THz communication models[16-19] cannot directly predict the transmission loss in the medium composed of plant leaves.

According to the simplified model of vegetation structure [20], vegetation can be summarized using varied parameters, such as leaf size, density, moisture content,and so on.In this paper, characteristics of attenuation under different vegetation species and air humidity levels are obtained by introducing the theoretical path loss model of THz radiation in vegetation and the molecular adsorption results of the THz wave in the air [21], incorporating channel composition of vegetation air and the structural species characteristics of the vegetation into the channel, and calculating the average attenuation of THz radiation in the mixed channel composed of air and vegetation leaves.

2.Vegetation attenuation

2.1 Vegetation structure abstract model

Studying vegetation attenuation requires abstract and unified modeling of the vegetation structures.Zygielbaum et al.[20] introduced a primitive abstract vegetation structure model which assumes that vegetation can be modeled as a series of concentric cylinders centered on stems.The number and radius of the cylinders depend on the size and angle of the average leaf of particular vegetation.Such a cylindrical model divides the vegetation into vertical regions (Fig.1), whereLis the blade length,θis the blade angle, andCis the number of cylinders.

Fig.1 Cylindrical model of vegetation

Therefore, in the most basic form, the structure of vegetation is considered to be composed of concentric cylindersCi, with the corresponding height and radius ofhiandri.The average leaf length is assumed to beLi, the distribution of average density of the leaves (the average number of blades per unit distance) isλi, the leaf angle isθi, and for each cylinder, the leaf angle is a constant value, with an assumption thatλ1<λ2<···<λi-1<λi, which means that the further the cylinder is from the center, the higher the density of the corresponding blades.

2.2 Vegetation path attenuation model

When the THz wave is transmitted through the vegetation, the attenuation mainly comes from the loss of free space, the scattering of uneven surfaces, and absorption by various materials (i.e., air molecules and leaves).These provide a theoretical total path loss model for the transmission of THz waves near vegetation, which can be described as follows:

wherefis the frequency,dis the transmission distance,PRandPTare the power spectral density (PSD) of the received signal and the transmitted signal, respectively,ASis the free space path loss,AMis the molecular absorption loss, andARis the scattering loss due to surface roughness of blade.

The conversion to dB is expressed as follows:

The medium of the transport path around the vegetation is mainly composed of air molecules and vegetation leaves [20], which is shown in Fig.2, wheredis the total path length andandrepresent the path length through the air and the blade, respectively.

Fig.2 Medium of the transport path around vegetation

The total attenuation coefficientα(f) of such a mixed channel can be defined as a function of the air absorption coefficientαaand the blade attenuation coefficient αl.

whereAandBrespectively represent the ratio of the transmission distance of the wave passing through the air and a blade to the total path length.The ratio of the transmission distance in the airAcan be calculated by the following expression:

The ratio of the transmission distance through the bladeBcan be calculated as follows:

wherenis the number of blades between the signal-generating device and the signal-receiving device, and in practice,nis randomly distributed depending on the statistical distribution of the blades in a particular species of vegetation.Considering that the thickness of a blade is on the order of micrometers, during transmission the path of the wave through the blade is negligible compared to the path through the air, i.e.,Bis negligible compared toA:

However, although the value ofBis small, its magnitude can significantly affect the signal attenuation.The air molecule absorption coefficient and the total attenuation coefficient of the blades are calculated separately as follows:

(i) Free space loss calculation

Free space path loss refers to the attenuation of signal power caused by the expansion of the wave in the transmission path when the signal propagates through the medium, resulting in a transmission loss.This loss can be defined as follows based on the Friis equation:

where c is the speed of light in a vacuum,Ptis the signal power of the transmitting antenna,Pris the signal power of the receiving antenna,dis the propagation distance,fis the signal frequency, 4πd2is an isotropic extension, and 4π(f/c)2is an antenna aperture term that varies with frequency and is expressed in dB as follows:

wherefis the frequency with its unit being Hz,dis the distance with its unit being m.

(ii) Absorption attenuation

When the THz band electromagnetic (EM) wave collides with the constituent molecules of the transmission medium, part of its energy is converted into kinetic energy and lost.This type of loss is called molecular absorption loss.Using the radiation transfer theory of the gaseous medium, it can be defined as follows:

The conversion to dB is expressed as follows:

whereαais the absorption coefficient of the medium,depending on the molecular composition of the air medium [22].

The absorption coefficient depends on the specific gas mixture that makes up the air and the concentration of the gas in the air.The absorption coefficient is directly related to the absorption loss of the medium, i.e., a larger absorption coefficient means a higher absorption loss and vice versa.The atmospheric polar molecular absorption coefficient can be calculated with a line-by-line integration method combined with the molecular spectral parameters provided in the HITRAN database [23] shown in Fig.3.

Fig.3 Atmospheric polar molecular absorption coefficient by the molecular spectral parameters provided in the HITRAN database

(iii) Attenuation coefficient of a vegetation blade

i) Leaf-absorption coefficient

Leaf-absorption coefficient composed of the absorption coefficient and the scattering coefficient, i.e., the total attenuation coefficient of the blade is calculated in the following manner:

The blade’s absorption coefficient defines the total attenuation of the THz signal when it collides with the vegetation blade.For a solid transmission medium, such as a blade, this parameter can be derived from the extinction coefficientklof the blade:

where the extinction coefficientklof the blade is a function of its dielectric properties, and αabsdescribes the amount of signal loss through the blade [24].This parameter can be based on the relative complex permittivityεlof the blade:

The real and imaginary parts ofεl(f) areεr(f) andεi(f).It can be seen from the above equation that to model the absorption coefficient of the blade, the relative complex permittivity of the blade must first be modeled.It is worth emphasizing that the relative complex permittivity is related to the frequency and can be measured in different ways.

ii) Complex permittivity

A leaf structure is composed mainly of air, water, and other compounds, such as sugar and protein [25], which have different dielectric constants, and such structures can be modeled as a mixture of water, air, and dry vegetation tissue, which are the most effective components of the EM waves.The dried vegetation tissue is a component of the dried compressed leaf.Using the effective medium theory, the complex permittivity of a variety of composite materials can be used as a function of the dielectric constant of the individual components.For the composite material of the blade, relevant studies [26]have shown the components affecting the transmission of EM radiation are air, water, and solid vegetation materials.

For a composite composed of two components, the complex permittivity can be approximated by the “LLL”model proposed by Landau, Lifshitz, and Looyenga [27].Since the blade composition is three-part, an extended version of the LLL model is applied in this paper [28].It is presented as a function of the volume fractionVof each component, and its corresponding relative complex permittivityεis calculated as follows:

where the subscriptsl,s,w, andarepresent leaf, solid vegetation material, water, and air, respectively.The relative complex permittivity of water in the THz band can be calculated by using the Jordens et al.[28] double-Debye model, which uses time-domain spectroscopy to measure the complex permittivity of solid vegetation materials.With the thickness of blades being between 100 μm and 220 μm, the measurement of frequency being 0.2 THz to 1.8 THz, and given the dielectric constant of the leaf tissue of the solid dried vegetation and the volume fraction of the leaf component, the above model applies to the calculation of the complex permittivity of any type of leaf.

iii) Blade-scattering coefficient

Since the wavelength magnitude of THz radiation in the sub-millimeter range is similar to the surface roughness distribution of vegetation leaves, the scattering causes partial loss to the THz wave.This type of loss is called surface-roughness scattering, and the blade-scattering coefficient can be expressed as follows [29] by Rayleigh roughness factor:

where∆ε(f) represents the amount of change in the dielectric constant,σlrepresents the standard deviation of the height of the blade profile,φandfrepresent the angle and frequency of the incident wave, respectively, andTis the average thickness of the blade.

In summary, when the THz wave is transmitted through vegetation, the mixed attenuation coefficient is represented as follows:

whereAandBrespectively represent the ratio of the transmission distance of wave through air and blade to the total path length, which can be calculated with (5) and(6), respectively,αais the air absorption coefficient, andαlis the attenuation coefficient of the blade.This paper uses the measured values given in [28], and the results are shown in Fig.4.

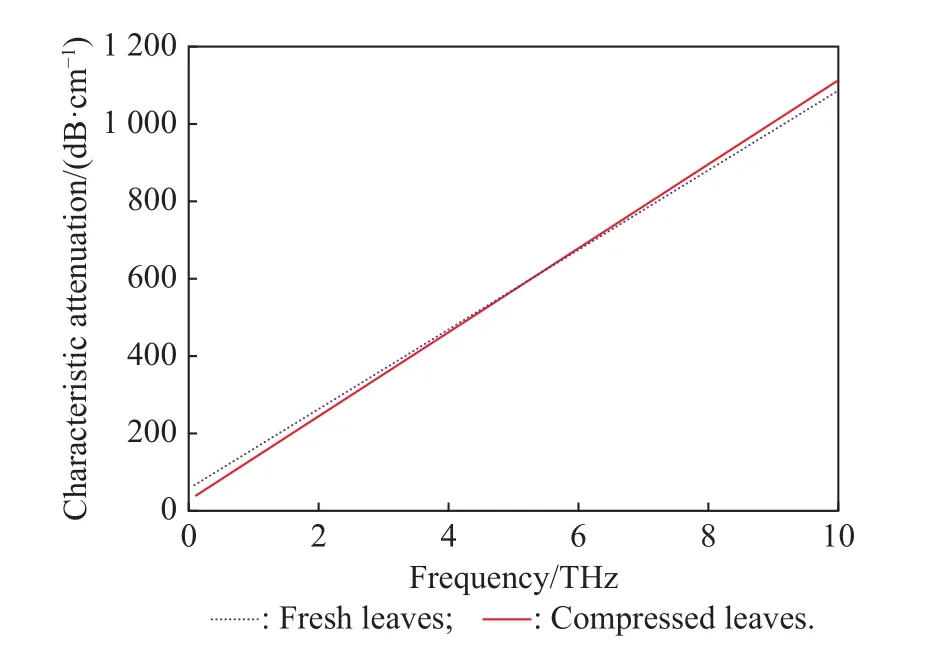
Fig.4 Characteristic attenuation of fresh and compressed leaves as a function of frequency

In the transmission distance ofd, the total vegetation attenuation model of the THz wave can be presented as follows:

which can be expressed in dB as follows:

3.Simulation and result analysis

As the transmission environment changes, various parameters also change, such as the average number of bladesn,thicknessT, and the moisture content of the mediumw.Here, the proportion of moisture in the air and the path through the leaves and air will change.This study focuses on the water content of the air and the path ratioBthrough the vegetation leaves to measure their effect on the total path loss.Assume that relative humidity (RH)values are 10%, 40%, and 70%.The path ratioBthrough the blade can be considered to be 0, 0.001, 0.002, 0.003,0.004, and 0.005.That is six blade densities.B=0 is the no-blade occlusion with only absorption and attenuation of the water molecules in the air.Coffee leaves are selected as the vegetation for the experiments, because coffee leaves can live in different relative humidity, and the average leaf number can vary from 15 to 50.The attenuation coefficient of the mixed medium composed of air and blades is calculated by using (20).

The attenuation coefficient of the mixed medium shown in Fig.5 is in good agreement with the measurements from prior studies [30].

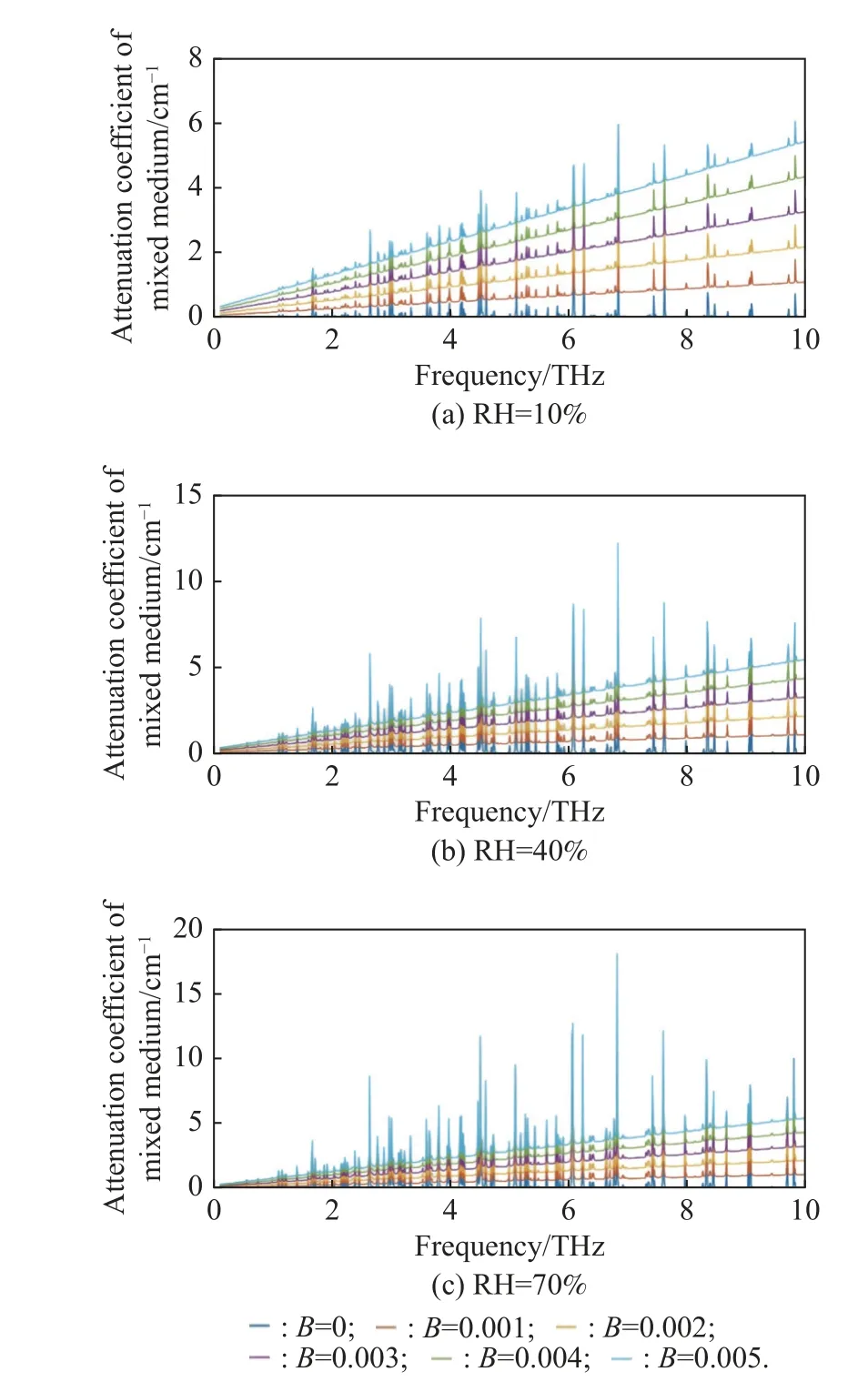
Fig.5 THz wave attenuation coefficient as a function of frequency through a mixed medium consisting of different humidity air and fresh coffee leaves

It can be observed that whenB=0, the absorption of water in the air is the only source of attenuation.The THz wave is transmitted in this environment with multiple transmission windows of different widths.WhenBis not 0, the path attenuation sources include water absorption attenuation and blade absorption and effects.Baffects the magnitude and slope of the attenuation factor without affecting the size of the attenuation window.It can be observed that in the THz band, the effect of the blade on the attenuation coefficient is linear, while the absorption of air molecules is characterized by the frequency selectivity.

The total path attenuation of THz waves transmitted in vegetation is calculated, and Fig.6 shows the path for a ratioBof 0.001 and 0.005 and an atmospheric RH of 40% and 60%.

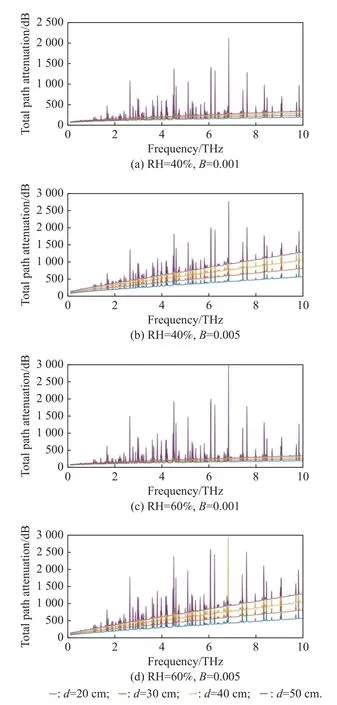
Fig.6 Total path attenuation for air path ratio B of 0.001, 0.005 and atmospheric RH of 40% and 60%

It can be seen from the above figure that an increase in the content of air moisture and the proportion of the transmission path cause attenuation to increase significantly.When the water content in the air is fixed, a higherB(mean more leaves are transmitted through) leads to an increase in the path loss, which leads to a significant reduction in the effective transmission distance.When the value ofBis fixed, an increase in the water content in the air leads to a significant increase in the path loss at some discrete frequencies.The results discussed in [20,30]agree with this finding, and these frequencies are the strong frequency points of absorption of water molecules.In 45% of RH, the average blade number per unit distance is 15 pieces/m and 50 pieces/m, and the average blade thickness is 160 μm.The total path attenuation of a THz wave in vegetation with different transmission distances is calculated with (22) when the path ratiosAandBare fixed.When the distance of transmission through a mixed medium of air and coffee leaves is 20 cm,30 cm, 40 cm, or 50 cm, the path attenuation of a THz wave through the mixed medium composed of air and fresh coffee leaves at 0.21 THz frequency band is shown in Fig.7.It can be seen that the air absorption attenuation peaks are in the range of 0.5-0.6 THz, 0.7-0.8 THz,and 0.9-1 THz, respectively, and an increase in the average number of blades per unit distance causes the path attenuation to increase significantly.

The total path attenuation of a THz wave transmitted in vegetation under different leaf thicknesses is calculated by using (22) for 80% RH, an average of 10 leaves per meter, and a transmission distance of 1m.In the frequency band of 0.1-10 THz, the variation range of leaf thickness is 100-220 μm, and the variation of total path attenuation with frequency is shown in Fig.8, where the average number of leaves is 15 pieces/m, the average thickness of leaves is 160 μm, and the frequency band is 0.21 THz.

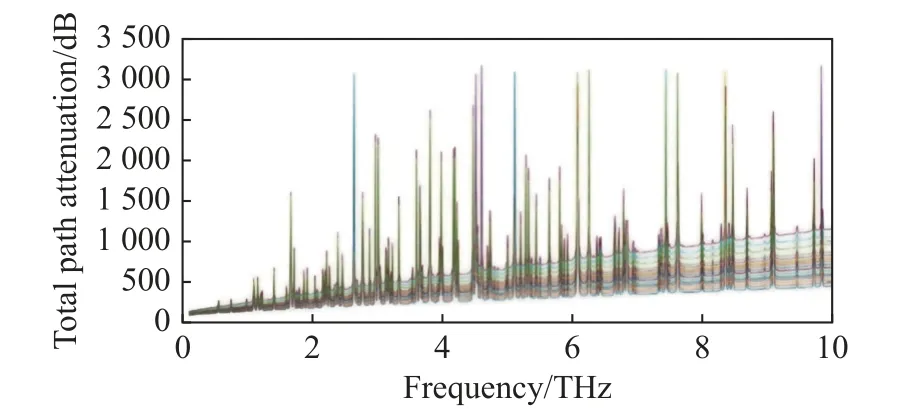
Fig.8 Total path attenuation of THz wave through a mixture of air and fresh coffee leaves

The analysis of the simulation results leads to a conclusion that with an increase in the transmission distance, the attenuation of a THz wave in a mixed medium composed of vegetation and air increases.With an increase in leaf thickness, the attenuation of a THz wave in vegetation also increases.

4.Conclusions

Based on the theoretical path loss model of THz radiation, this paper predicts an average attenuation of THz radiation in a mixed channel composed of air and vegetation leaves.The model considers channel composition and the physical properties of vegetation to calculate attenuation characteristics based on specific vegetation species, different humidity levels, and the water content of the air, the proportion of the path through the vegetation leaves, the number of leaves, and the average thickness of leaves vary in the paper to study their effect on the total path loss.The results show that air composition(in particular its moisture content) and the properties of leaves (the number of blades, thickness, and distribution)have a considerable influence on the path loss and the effective transmission distance.