Joint polarization and DOA estimation based on improved maximum likelihood estimator and performance analysis for conformal array

SUN Shili, LIU Shuai, WANG Jun, YAN Fenggang, and JIN Ming

School of Information Science and Engineering, Harbin Institute of Technology, Weihai 264209, China

Abstract: The conformal array can make full use of the aperture,save space, meet the requirements of aerodynamics, and is sensitive to polarization information.It has broad application prospects in military, aerospace, and communication fields.The joint polarization and direction-of-arrival (DOA) estimation based on the conformal array and the theoretical analysis of its parameter estimation performance are the key factors to promote the engineering application of the conformal array.To solve these problems, this paper establishes the wave field signal model of the conformal array.Then, for the case of a single target, the cost function of the maximum likelihood (ML) estimator is rewritten with Rayleigh quotient from a problem of maximizing the ratio of quadratic forms into those of minimizing quadratic forms.On this basis, rapid parameter estimation is achieved with the idea of manifold separation technology (MST).Compared with the modified variable projection (MVP) algorithm, it reduces the computational complexity and improves the parameter estimation performance.Meanwhile, the MST is used to solve the partial derivative of the steering vector.Then, the theoretical performance of ML, the multiple signal classification (MUSIC) estimator and Cramer-Rao bound (CRB) based on the conformal array are derived respectively, which provides theoretical foundation for the engineering application of the conformal array.Finally, the simulation experiment verifies the effectiveness of the proposed method.

Keywords: conformal array, maximum likelihood (ML) estimator,manifold separation technology (MST), parameter estimation,Cramer-Rao bound (CRB).

1.Introduction

Compared with the traditional polarization sensitive array, the conformal array antenna attached to the surface of the carrier can effectively save space, meet the aerodynamic requirements, expand the beam scanning range, achieve higher antenna gain, and obtain larger effective aperture [1-4].It has important applications in space-borne radar [5,6], missile-borne radar [7,8], aerospace aircraft [9,10], wireless communication [11], selfsteering [12] and other fields.As an important research direction, joint polarization and direction-of-arrival(DOA) parameters estimation of the conformal array has high application value [13-15].Classical parameter estimation methods are mostly based on omni-directional antennas, but conformal arrays are mostly based on directional antennas.Due to the curvature of the ML conformal carrier, the orientation of the array element is inconsistent.Many classical algorithms cannot be directly applied to conformal arrays.The main difficulties in parameter estimation of the conformal array lie in computational complexity and array geometry limitation, which limits practical engineering application.

At present, in the existing literature, the main results of conformal array parameter estimation are virtual interpolation method, nested subarray method, tensor model method, parallel factor (PARAFAC) method, geometric algebra method, etc.In the virtual interpolation aspect, a DOA estimation method for cylindrical conformal array is proposed [16,17], which exploits sub-array divided technique and estimating signal parameters via rotational invariance techniques (ESPRIT) for the virtual omnidirectional array.However, it only considers the amplitude information of the antenna element, and the polarization information in the radiation pattern is ignored.Aiming at this problem, a parameter estimation method using dual-polarized conformal array and combining virtual interpolation with spatial smoothing technology was proposed [18].However, this kind of algorithm requires smaller interpolation sector in exchange for estimation accuracy, thereby it has great limitations in engineering.Then, the method of nested subarray drew attention.In[19], underdetermined DOA estimation for conformal array was implemented by using nested array rules.In[20], A high-accuracy DOA estimation method for cylindrical conformal is presented by introducing nested subarray structure, which avoids spectral peak search.In[21], an innovative two-dimensional (2D) DOA estimation method for cylindrical conformal array based on tensor model was proposed, which utilizes multidimensional information to improve the accuracy of parameter estimation and is suitable for unknown mutual coupling conditions.In other aspects, Zou et al.[22,23] extended the PARAFAC theory into the DOA estimation of conformal array, estimated the mutual coupling coefficient and improved the estimation accuracy.Most of the above algorithms rely on special structures, require more array elements, and ignore the estimation of polarization parameters [24].

In [25], a noteworthy parameter estimation method called manifold separation technique (MST) was proposed, which pointed out that the array signal steering vector can be decomposed into the product of sampling matrix and Fourier basis.Then one-dimensional DOA estimation using uniform circular array was realized.This idea decouples angle information and the array’s own information including radiation pattern, mutual coupling,etc., thereby it has high research value.In [26,27], the MST was expanded to 2D, and the modified variable projection (MVP) algorithm was proposed based on MST to achieve rapid DOA estimation iteratively.Furthermore,to achieve joint estimation of polarization and DOA,Costa et al.[28] extended the MVP algorithm based on MST to four dimensions.However, it requires the multiple signal classification (MUSIC) algorithm to provide an initial value, and the iterative convergence rate slows down with the increase of sampling points and the number of sources.

In addition, investigation on the performance of parameter estimation algorithms and the Cramer-Rao bounds(CRB) has great significance to conformal array structure design and performance optimization.In this respect,Ziskind et al.[29] gave the theoretical performance of the MUSIC algorithm and the CRB by special antenna radiation patterns without considering the influence of other parameters.The CRB of conformal arrays were also discussed in [22,23], but the expressions for partial derivative of the steering vector were not given directly.Moreover, it becomes more difficult to obtain the partial derivative of steering vector as the non-idealities of array increase.

In summary, it is difficult for most of the existing conformal array parameter estimation methods to take into account the reduction of computational complexity, arbitrary array geometry, and the estimation of polarization parameters simultaneously.Although the MVP algorithm solves the above problems, it needs to be improved in terms of initial value and iterative convergence rate.In terms of the conformal array’s performance analysis, the main difficulty is that the partial derivative of the steering vector to the parameter cannot be expressed directly.

In this paper, we devise an improved maximum likelihood (ML) method based on Rayleigh quotient.The proposed method rewrites the cost function of the ML from maximizing the ratio of quadratic forms into minimizing the quadratic form.Then, rapid parameter estimation is achieved through the idea of the MST and the iterative process in the MVP algorithm is avoided.The MST is also adopted to solve the difficulties in obtaining the partial derivative of the steering vector, and the performance of the MUSIC, the ML estimator, and CRB for the conformal array are derived respectively based on the partial derivative.

The main contributions of this paper are summarized as follows:

(i) The received signal model of the conformal array under the wave field model is established.

(ii) An improved ML estimator with low computational complexity is proposed in the case of single source,which avoids the iteration process in the MVP algorithm.

(iii) Estimation performance of the MUSIC, ML estimator, and CRB for the conformal array are derived.

2.Signal model of conformal array

Assume thatKnarrowband far-field signals are incident on an arbitrary structure conformal array withMelements as shown in Fig.1.

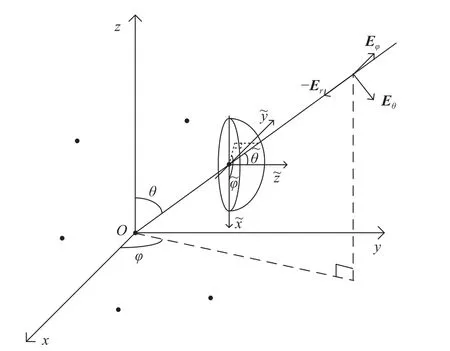
Fig.1 3D arbitrary shape array coordinate system diagram

The incident signal parameter is(θ,φ,γ,η)={θk,φk,γk,, where θ ∈[0,π]and φ ∈[0,2π) are elevation and azimuth.γ ∈[0,π/2]and η ∈[0,2π] are auxiliary polarization angle and polarization phase difference, respectively.In a real environment, the signal steering vector of the conformal array is composed of the spatial steering vector and the polarization steering vector affected by antenna radiation patterns, which include wave path difference and amplitude-phase gain, respectively [22].Then, the received signal model withNsnapshots can be written as

As shown in Fig.1, different antenna elements may have inconsistent orientation patterns, and (θ˜,φ˜) represents elevation and azimuth in local coordinates, respectively.

Most of the existing parameter estimation algorithms for conformal array are based on the above model.In this paper, a more applicable model called the wave field model is adopted to decouple DOA information and polarization information [28].The above model can be further expressed as wave field models:

It is pointed out that the spatial steering vector of any array can be composed of a sampling matrix depending on the array information and a 2D Fourier basis depending on the angle information [25], which can solve array non-idealities such as mutual coupling effect, inconsistent of radiation patterns.Combining the wave field model and the MST, the steering vector for conformal array in (5) can be expressed as

where Γ=[Γ1,Γ2] is the sampling matrix obtained by 2D inverse discrete Fourier tranform (IDFT) of the sampling horizontal and vertical polarization steering vector,respectively.And they also denote the coefficients for Fourier expansion of the corresponding steering vector,which are independent of DOA and polarization information and depend only on the array structure.d(θ,φ) is the 2D Fourier basis.MeandMaare the truncation lengths of Fourier bases in elevation and azimuth dimension.⊗denote Kronecker product.The construction method of the sampling matrix was introduced in [26].

From (1) and (8), the received signal model of the conformal array can be written as

where

andd(θk,φk) is defined in (10).H(γ,η)=[Hh,Hv]Trepresents the signal polarization matrix and can be found as

Then, the ML estimate for the covariance matrixRˆxxof array output withNsnapshots under the narrowband farfield assumption is

3.Improved ML estimator and CRB

3.1 Improved ML estimator

The ML estimator has excellent parameter estimation performance.In the case of single source, with the utilization of the cyclicity of the matrix trace, the cost function of the classical ML algorithm [30] is as follows:

In [28], an efficient algorithm based on the MVP algorithm and MST was proposed to avoid multi-dimensional search.However, it requires iterative process, sets iterative convergence bounds, and the iterative speed decreases when the number of sampling points is large.

In this paper, an improved ML estimator based on MST is proposed, which realizes fast parameter estimation and avoids iterative process in the MVP algorithm.The extremal problem of quadratic forms with rank deficiency property can be quickly realized by MST, which reduces the computational complexity [28].If (14) can be transformed into an extremal problem of quadratic forms with rank deficiency property, the fast parameter estimation can be realized.This method is feasible.

According to the properties of Rayleigh quotient, (14)satisfies

where λmax(Rˆxx) represents the maximum eigenvalue ofRˆxx.It can be proved that the equal sign in (15) holds up if and only if ξ takes the true value.Considering thatbHb>0 and multiplying both ends of (15) bybHb, we can get

By taking (8) into (16), (15) can be equivalently transformed into

When ξ takes the true value, we can gethHHh=0 and det(H)=0 , which means thatHis positive semidefinite.When ξ does not take the true value, we can gethHHh>0 and det(H)>0 , which means thatHis positive definite.Therefore, the cost function of the proposed approach can be expressed as

Therefore, the ML estimator in (14) is transformed from the problem of maximizing the ratio of quadratic forms to those of minimizing the quadratic form.

Then, rapid parameter estimation can be achieved with the help of MST.

We define the matrixGas the square root of the matrixwhich satisfies

and the determinant of (18) can be expressed as

where

where

representsthesumof theblock elements of thekth block diagonal in thematrix

represents the sum of the elements of thelth diagonal in the matrix

to replace convolution operation.

Cijin (23) is given by

where ∗ denotes the convolution operation.FFT2{·} and IFFT2{·}denote 2D FFT and 2D inverse fast Fourier transform (IFFT), respectively.

The details on the proof of (23) and (26) can be found in [28].Take (22) into (21) to obtain

Similar to (22) and (26)，we extract Fourier bases and there is

Equation (28) shows that the determinant ofH(θ,φ)corresponding to elevation and azimuth angles can be expanded by 2D discrete Fourierm transform (DFT), and theFouriercoefficientmatrixCΓonlydepends onthe received signal,which isindependentofthe angle.Therefore, the ML spectral function can be quickly calculated by 2D FFT.

The location of the peak is the estimation of the elevation and azimuth angle.Zero padding can be performed according to the required search step size.

According to the related properties of the quadratic form, the estimation of polarization parameter can be obtained by the normalized eigenvectoruˆ corresponding to the minimum eigenvalue ofHˆ:

The improved ML estimator avoids the iterative process in the MVP algorithm, and can directly calculate the spectral function through FFT, so as to achieve rapid parameter estimation.

The proposed algorithm is summarized as follows.

Algorithm 1 Improved ML estimator ˆRxx 1.Calculate the signal covariance matrix and find the maximum eigenvalue.λmaxI- ˆRxx G 2.Calculate the matrix and find its square root.Cij CΓ 3.Find according to (26) and calculate according to (29).CΓ 4.2D-FFT is performed on to obtain the ML parameter estimation spectrum, and then the DOA estimation is obtained as.5.Use (32)-(34) to perform eigenvalue decomposition to obtain the polarization parameter estimation of the signal.(ˆθ,ˆφ)

The computational complexity of the improved ML estimator isO(Qlog2Q) andQdenotes the number of Fourier transform points.The MVP algorithm requires the polarimetric element-space (PES) MUSIC algorithm to provide initial values, so the computational complexity isO(Qlog2Q)+O((MeMa)MK) [28].Benefiting from FFT, the improved ML estimator has good real-time performance without iterative process.

3.2 Performance analysis

In this subsection, the theoretical estimation error variance of the MUSIC, the ML estimator, and CRB for conformal array are investigated based on MST, which determine the lower bound of the parameter estimation performance of the given algorithm and those of a given array,respectively.The performance analysis for conformal array is of utmost significance to array designing and optimization.The main difficulty of performance analysis for conformal array is solving the partial derivative of steering vector.

Taking the elevation as an example, the partial derivative of steering vector is as follows:

wherepk=[p1k,p2k,···,pMk]T.It can be seen from (7)that the response of the pattern in the global coordinate system needs to be obtained through two Euler rotation transformations and the pattern expression is more complicated due to non-idealities such as mutual coupling.Therefore, the partial derivative of the array steering vector and the CRB for conformal arrays cannot be expressed directly.

The MST can decouple the array information, DOA,and polarization information.The array steering manifoldBis decomposed into the combination of the sampling matrix Γ and the 2D Fourier basisD(θ,φ).The sampling matrix Γ is independent of DOA information.Thus, the partial derivative of the steering vector to angle can be transformed into those ofD(θ,φ).For any conformal array, the partial derivativeJBofBto unknown parameters ξ can be written as

where

whereZ=[IK,IK,IK,IK],Rsrepresents the signal covariance matrix and σ2nis the noise power.The expression(39) in [28] is suitable for the case that the sampling points are small.The dimension of Ψ increases sharply as the number of sampling points increases which leads to high computational complexity, because a large number of unnecessary zeros are generated in the process of calculating Ψ.For example, it can be seen from (39) that if the sampling points isMaMe=180×180, the dimension of Ψ will be 64 800×129 600 , most elements of Ψ are zeros.

In fact, Ψ represents the partial derivative factor and denotes the weighting of the Fourier basis, so the product operation in (38) can be replaced by the Hadamard product to avoid unnecessary zero.We can re-express the invariant Γ Ψ in (37) as

where no extra zero is generated and the computational burden is greatly reduced with more sampling points.In[31], the variance of the theoretical parameter estimation error of the MUSIC and the ML estimator under the subspace fitting framework were proposed.In this paper,they are expanded to four dimensions with the help of MST which solves the difficult problem of partial derivatives.The estimated variances of the MUSIC algorithm and ML estimator for the conformal array are

whereCMUSICis the estimated variance of the MUSIC,andCMLis the estimated variance of the ML algorithm.

4.Simulation

In this section, some numerical experiments are conducted to verify the effectiveness of the proposed algorithm.First, the spectrum of the improved ML estimator is validated by (19) in a common scenario.Second, the performance of the proposed improved ML estimator is examined with comparison between the MVP and CRB.The root mean square error (RMSE) of ξ is used to evaluate the performance.Third, since (42) and (43) can be used to study the theoretical performance of various algorithms under different conditions, a typical scenario is considered, where the signal-to-noise ratio (SNR) versus correlation coefficients for the MUSIC and the ML estimator are drawn.

4.1 Validation of improved ML estimator

In this subsection, the parameter estimation performance of conformal array under single source is studied to verify the effectiveness of the proposed algorithm.

The simulation experiment conditions are as follows.The cylindrical conformal array is adopted as shown in Fig.2.

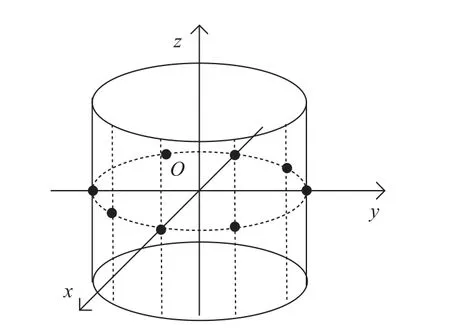
Fig.2 Cylinder conformal array

The number of circular arrays is one without losing generality, the number of array elements is eight, which are evenly distributed on the circular ring with a radius of 2λ.The radiation patterns of each array antenna [18] are

when 0 ≤θ ≤π/2 and

when θ>π/2.J0is the zero order first Bessel function,andJ2is the second order first Bessel function.

The incident signal parameters are(θ,φ,γ,η)=(30◦,50◦,45◦,30◦)with 100 snapshots and SNR = 15 dB.The number of elevation dimension and azimuth dimension sampling points is 180.The improved ML estimator spectrum is shown in Fig.3

Fig.3 Spectrum of the improved ML estimator

As shown in Fig.3, the proposed algorithm can successfully estimate the angle.Then, through (33) and (34),we can get polarization parameter γˆ=45.129◦and ηˆ=30.000 8◦.

4.2 RMSE of improved ML estimator for conformal array

In this subsection, the statistical performance of conformal array parameters estimation under single source is investigated.

Experiments with 300 independent Monte Carlo trials are implemented to examine the performance of the MVP algorithm and the proposed ML estimator.The same conformal array is considered with 50 snapshots and the SNR varies from -10 dB to 10 dB.Then, the RMSE of the parameters and CRB are shown in Fig.4.

Fig.4 RMSE and CRB versus SNR

It can be seen from Fig.4 that the proposed method obtains the same performance as the MVP algorithm.The algorithm proposed in this paper and the MVP algorithm in [28] are two different implementations of the ML estimator, therefore, they share similar performance.The RMSE and CRB gradually decrease as the SNR increases, which means that the parameter estimation is more accurate.The parameter estimation performance is slightly worse when the SNR is low, which is caused by small snapshots.

4.3 Theoretical performance of different algorithms

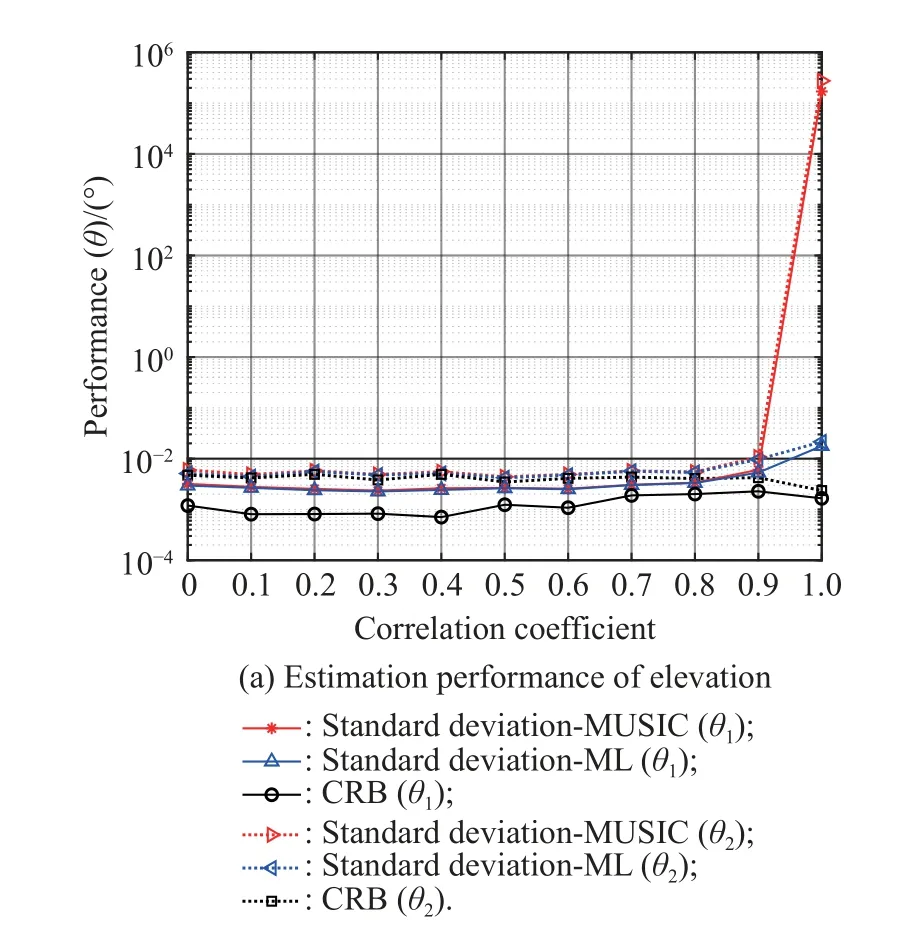
In this subsection, the theoretical performance of the MUSIC and ML is illustrated to study the applicability of different algorithms under different correlation coefficients.Two equal power sources are incident on the cylindrical conformal array, the angle parameters and polarization parameters are

The SNR of the two sources is fixed at 20 dB and other conditions are the same as those in Subsection 4.2.

CRB and the theoretical standard deviation are chosen to investigate the theoretical performance of MUSIC and ML estimator, which are defined as

where ξirepresents theith element of ξ=[θ,φ,γ,η]

It can be seen from Fig.5 that the MUSIC algorithm can effectively estimate the parameters when the correlation coefficient is less than 0.9, but the algorithm fails when the correlation coefficient is greater than 0.9 and the ML estimator is not sensitive to signal correlation,which theoretically proves the adaptability of the MUSIC algorithm and the ML algorithm to different correlation coefficients.The study for the variance of the theoretical parameter estimation error is of great significance to the selection of the algorithm in engineering.

5.Conclusions

In this paper, the MST and wave field model are introduced into the conformal array to decouple the array structure, DOA and polarization information.On this basis, an improved ML estimator is proposed which can convert from the problem of maximizing the ratio of quadratic forms to those of minimizing quadratic forms for the case of single source.Compared with the existing method, it avoids iteration, directly uses the FFT to calculate the 2D DOA spectrum, and reduces the computational complexity.Then, by introducing MST, the partial derivative of the conformal array steering vector is well solved, and the theoretical estimation variance of the MUSIC, the ML estimator, and CRB are derived, which provides a theoretical basis for the design and performance optimization of conformal array structure.Numerical simulation results demonstrate the effectiveness of the proposed algorithm.