基于正交试验的透平叶片气膜冷却仿真与预测
王正杰 何洪斌 张席 陈洁怡
(沈阳航空航天大学航空发动机学院 辽宁沈阳 110136)
0 引言
透平作为电厂燃气轮机核心部件,其导向叶片一直处于高温、高压、高速的工作环境中。要保证透平安全可靠地运行,最常见的保护措施就是采取气膜冷却,即从热表面的孔隙中吹出冷气流,以阻隔燃气对固体壁面的加热[1]。找到最佳的孔参数和气动参数,设计出可承受更高温度的涡轮部件是一个重要研究课题。
贺宜红等[2]研究了不同湍流度下吹风比对涡轮叶片气膜冷却的影响规律。邓宏武等[3]研究了涡轮叶片在旋转状态下不同吹风比的气膜冷却特性。赵洪利等[4]分析了叶片吸力面气膜冷却规律,发现小吹风比下主流湍流度增大,气膜冷却效率降低。张玲等[5]利用正交模拟的方法模拟了槽宽、吹风比和槽深3 因素共同作用下平板气膜冷却效果。秦晏雯等[6]采用BP 神经网络对多参数变化下的气膜冷却效率进行了预测,发现神经网络模型预测精度优于经验公式且适用范围广。王昭等[7]提出了基于粒子群优化算法(Particle Swarm Optimization,PSO)优化反向传播(BP)神经网络的火箭冲压发动机推力估计方法。
透平工作环境复杂,目前对多因素同时影响下的冷却效率的研究较为复杂,直接研究不同工况组合时需要做大量的实验。基于此,本文以某透平导向叶片为研究对象,采用正交试验的方法简化实验工况,使用COMSOL 软件数值模拟气膜孔角度,吹风比和湍流强度3 个因素共同影响下的冷却效果,得到最优冷却方案。使用神经网络对全体工况进行预测,极大地提高了工作效率。
1 计算模型及方案
1.1 计算模型及网格划分
如图1 为某叶片气膜孔示意图,叶片弦长C 为74 mm,展向长度H 为110 mm,气膜孔布置在吸力面距叶片前缘17%相对弧长处,与叶片型面夹角为射流角α,气膜孔孔径D=2 mm,孔间距H1=7 mm,孔数为9。模型网格如图2 所示,计算域网格在壁面附近采用结构化网格,在主流通道和气膜孔使用非结构化网格,并且在气膜孔附近和壁面附近都进行网格加密处理。经网格无关性验证,最终选择计算网格数为311 万。

图1 叶片气膜孔示意图
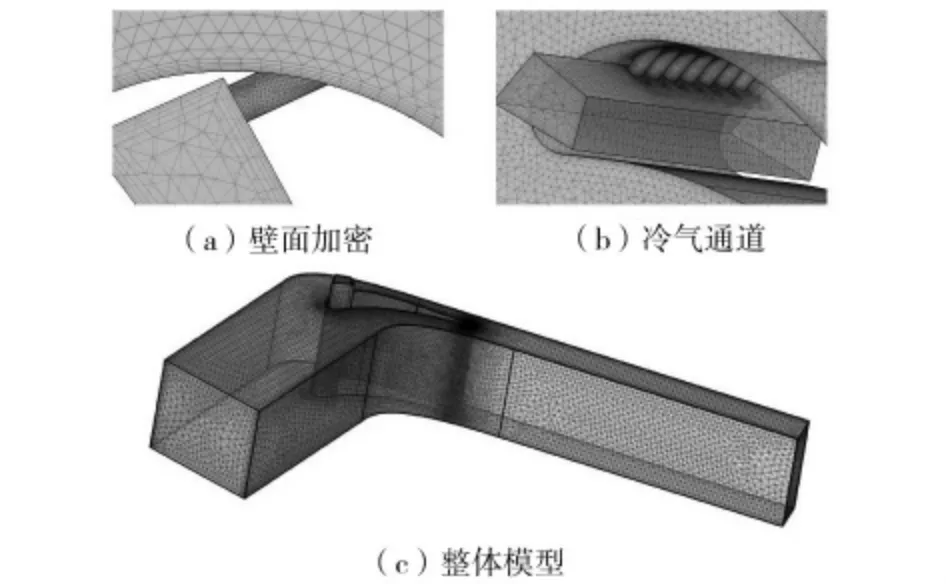
图2 模型网格
1.2 计算方法及边界条件
采用COMSOL 软件稳态计算,RNG k-ε 湍流模型能模拟撞击、分离流、二次流和旋流等复杂流动[8],因此湍流模型采用RNG k-ε 模型。使用线性形函数求解流体速度场和压力场,流体传热采用线性单元离散化,近壁面采用壁面函数。
图3 为叶片气膜孔计算模型,该模型由主流通道、冷气通道及圆柱孔组成。主流入口为速度入口,速度为10 m/s,温度为330 K;出口为压力出口,压力为1.013×105Pa;冷却气体入口速度由吹风比计算得出,温度为300 K;工质使用不可压缩气体,两侧壁面为周期性壁面,其余壁面条件为绝热。

图3 计算模型
1.3 参数定义
气膜冷却效率定义见式(1)。
式中:T∞为主流温度;Taw为绝热壁温;Tc为冷气温度;T 为燃气与冷气掺混温度。
展向平均气膜冷却效率定义见式(2)。
式中:ηi为展向第i 点的冷却效率;n 为展向点数。
吹风比定义见式(3)。
式中:ρc为冷气密度;ρ∞为主流密度;uc为气膜孔出口平均速度;u∞为主流速度。本文取ρc=ρ∞。
冷却气体入口速度定义见式(4)。
式中:n 为气膜孔数量;Ac为气膜孔出口面积;A2为冷气腔入口面积。
1.4 计算方法验证
为验证本文数值模拟方式的准确性,与文献实验数据[9]进行对比,图4 为吹风比0.5、射流角30°时,数值计算结果与实验数据对比。趋势基本吻合,平均误差为7%,说明本文所选用的计算方法准确性较好,可以用于后续计算。
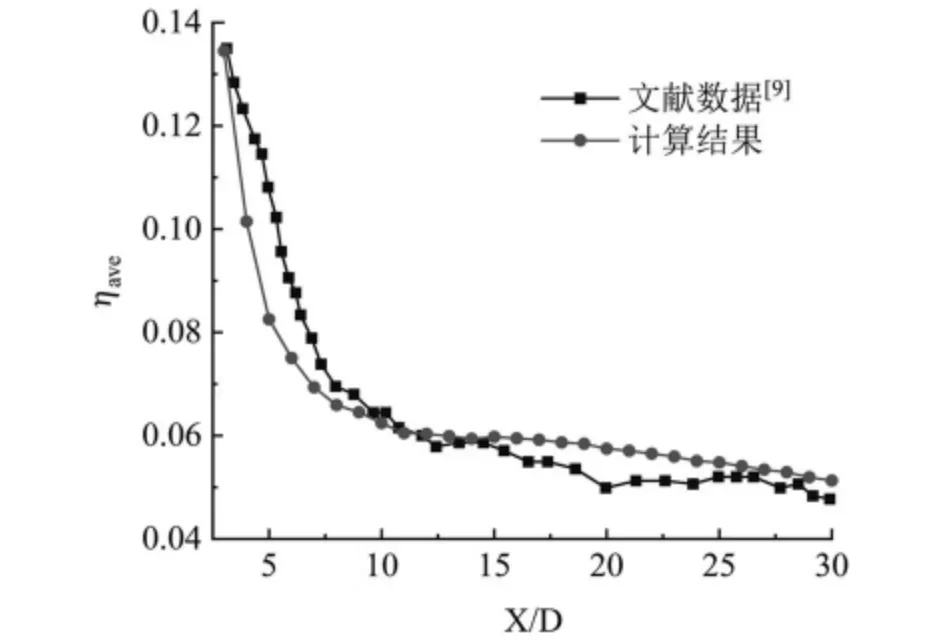
图4 数值计算结果与实验对比
1.5 计算方案
本文研究的是1 种三因素三水平实验,按全面实验需要27 种组合。为了节省计算资源,使用正交设计方法设计实验方案。正交设计可以根据正交性,选择一部分具有代表性的组合进行实验,是1 种高效率实验设计方法[10]。使用正交设计安排1 种三因素三水平的实验只需9 种组合实验,大大节省了计算资源。
正交表代号为Ln(qm),L 表示正交表,n 表示实验次数,q 表示水平个数,m 表示因素个数。3 种影响因素分别是射流孔角度,吹风比和湍流强度。射流孔角度为30°、45°、60°,吹风比0.4、0.6、0.8,湍流强度0.01、0.05、0.10。正交试验计算方案见表1。
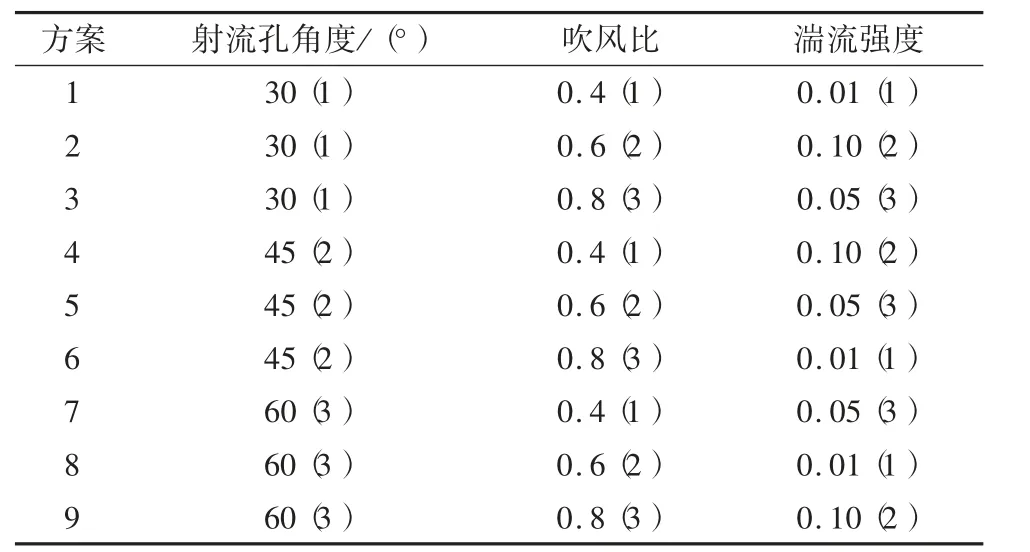
表1 L9(33)正交表影响因素
2 计算结果分析
2.1 冷却效率的正交分析
如表2,9 种方案中,平均冷却效率最低为0.582 6,气膜孔角度60°,吹风比0.8,湍流强度0.1(方案9);区域平均冷却效率最高为0.643 4,气膜孔角度30°,吹风比0.6,湍流强度0.1(方案2);方案2 相比方案9 冷却效率提高了约10%。

表2 正交试验结果
表3 中Ⅰ、Ⅱ、Ⅲ分别为表1 中各列数字“1、2、3”相应模拟试验指标之和的平均值,R 为极差。通过对比极差可得影响叶片冷却效率主次顺序为:气膜孔角度>湍流强度>吹风比。可见,气膜孔角度的设计对于冷却效率影响起着至关重要的作用。

表3 试验结果极差分析
图5 为各因素水平平均展向气膜冷却效率,由图5(a)可以看到,在气膜孔角度单独影响时,气膜孔角度为30°时冷却效率最好,这主要是由于小角度是气膜有更好的贴壁性;由图5(b)可以看到,在靠近气膜孔处吹风比M 为0.4 时冷却效果最好,远离气膜孔处吹风比0.8 时冷却效果最好,这主要是由于在大吹风比时射流喷得更远并在气膜孔后方形成旋涡;由图5(c)可以看到,湍流强度L 为0.1 的冷却效果最差,这是由于湍流度增大时,会降低贴壁效果。

图5 各因素水平平均展向气膜冷却效率流场分析
2.2 流场分析
2.2.1 温度场分析
为了揭示最佳方案可以取得好的气膜冷却效果的机理,本文将最佳冷却方案和最差冷却方案的温度场和速度场进行对比分析。图6 和7 分别为在流向截面处和壁表面的等温线分布云图。从图6 可以看到方案2 射流的低温核心区和壁面很近,温度较低贴壁性较好,射流核心区呈长丝带状;而方案9射流低温核心区和壁面有很大的距离。从图7 可以看到,和方案9 相比,方案2 的展向冷却效果更好且能够延伸更长的距离,使聚敛区域扩张。这是由于随着射流孔角度和吹风比的增加,沿射流孔中心线方向的气体动量增加,进而使射流的曲率半径R 大于吸力面壁面的曲率半径,不利于气膜的附着,导致方案9 的冷气并没有紧贴壁面流动。

图6 流向截面温度分布
2.2.2 速度场分析
图8 为流向壁面的速度云图。可以看出方案2 的漩涡较少,而方案9 在射流孔下游形成了明显的漩涡。这是由于方案2 射流孔角度和吹风比较小,射流沿垂直叶片型面方向的气体动量小,主流方向动量大,射流气体有更好的贴壁性;而方案9射流沿垂直叶片型面方向的气体动量大,射流抬离壁面,在射流气体和壁面之间和主流形成压力差,从而形成了漩涡,降低了冷却效果。

图8 壁表面速度分布
图9 和图10 分别为方案2 和方案9 流向截面处和气膜孔下游距离气膜孔长度D 的展向截面处速度矢量图。从图9中可以看到方案2 射流对主流速度场的影响很小,射流气体能更好地附着在叶片表面;从图10 可以看到方案9 在射流孔下游形成明显的漩涡,这是因为射流沿垂直叶片型面方向的气体动量大,射流的流体抬离壁表面,进而使叶片表面压力降低,在压力差的作用下,将射流两侧的主流高温气体卷吸到壁面。
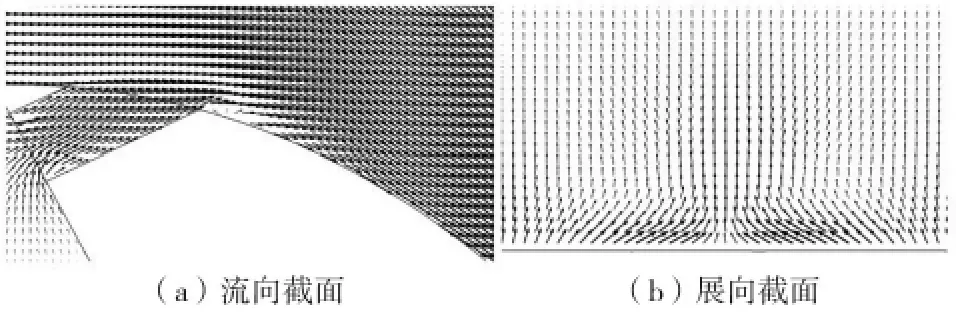
图9 方案2 速度矢量分布图
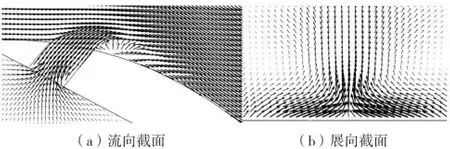
图10 方案9 速度矢量分布图
3 基于PSO-BP 的气膜冷却效率预测
影响气膜冷却的因素众多,难以维持线性关系,现有的经验公式对气膜冷却的拟合效果较差。BP 神经网络模型结构简单,对非线性模型的处理能力较强。PSO 优化算法参数较少,全局搜索能力强,被广泛用于神经网络的优化。本文将正交实验的9 种方案数值计算所得189 组数据随机划分为训练集和测试集,训练集135 组,测试集54 组,建立PSO-BP 预测模型。
将本文数值模拟得到的9 种组合下数据作为样本数据。首先进行归一化,然后设定各个算法的参数;其次建立神经网络模型,以流向位置S/D,气膜孔角度,吹风比,湍流强度为自变量,冷却效率为因变量,带入PSO 优化算法计算适应度,进行迭代,以得到最优初始阀值权值,将最优初始阀值权值赋予神经网络模型进行训练。
图11 为测试集54 组数据的预测结果与真实值冷却效率对比图,平均相对误差为2.77%,整体预测精度较高。图12 为气膜孔角度60°,吹风比0.8,湍流强度0.10(方案9)和气膜孔角度30°,吹风比0.6,湍流强度0.10(方案2)时预测值和实际值的对比图,可以看到其不仅在趋势上吻合较好,而且误差较小,在气膜冷却方面具有良好的应用前景。最后使用此模型对其它18 种组合的冷却效率进行预测,预测结果如表4。
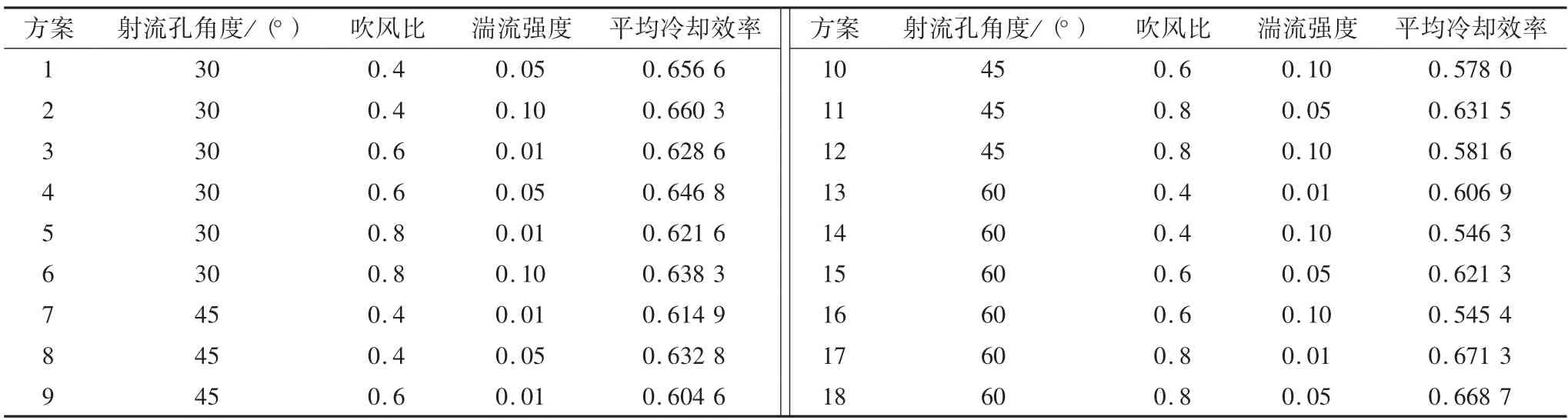
表4 神经网络预测结果
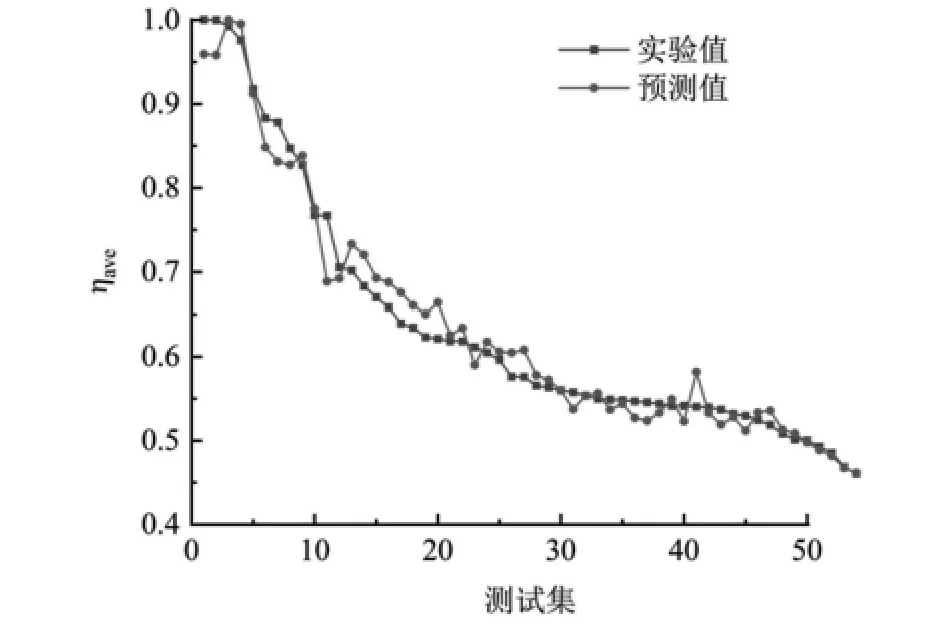
图11 测试集预测结果与真实值对比

图12 神经网络预测结果与实验结果比较
4 结论
本文通过数值计算研究,得到如下结论:
(1)在正交设计实验组合中,气膜孔角度30°,吹风比0.6 和湍流强度0.10 为3 个因素共同作用下最优冷却方案,叶片表面平均冷却效率为0.6434;气膜孔角度60°,吹风比0.8 和湍流强度0.1 的冷却效率最低,为0.5826,比最优冷却方案低约10%。
(2)影响叶片表面冷却效率因素的主次顺序为:气膜孔角度对冷却效率的影响最大,湍流强度的影响较小,吹风比的影响最小。
(3)提出了1 种基于PSO 优化BP 神经网络的气膜冷却效率预测模型,使用该模型预测了本文研究工况下其它18 种组合的冷却效率。结果表明,该模型预测精度较高,训练集平均误差为0.8%,在气膜冷却方面具有良好的应用前景。

