火灾高温后钢筋混凝土梁的残余抗弯承载力预测*

刘召伟 郭星星 韩岩青 刘倩倩 武 宁 刘朝峰

(1.中国路桥工程有限责任公司, 北京 100011; 2.河北工业大学土木与交通学院, 天津 300401; 3.青岛市地铁四号线有限公司, 山东青岛 266030; 4.丰宁满族自治县交通运输局, 河北承德 068350)

0 引 言

钢筋混凝土(Reinforced Concrete, RC)梁是现代结构的主要承重构件,突发火灾对其承载能力与耐久性会造成不同程度损伤,从而降低了建筑结构的安全可靠性[1-2]。火灾后RC梁的抗弯承载力不仅与钢筋、混凝土材料的力学性能退化及其界面黏结退化相关,还与混凝土高温爆裂导致构件几何尺寸、质量损失及温度场变化等有关[3-5]。因此,研究火灾高温后RC梁的抗弯承载力变化,对准确评估RC梁灾后力学性能及安全性具有重要意义。

目前,钢筋、混凝土等材料及其组成构件高温下/后的温度场及力学性能研究较多,但还需深入研究火灾后钢筋/混凝土界面黏结退化、混凝土爆裂、受火时间等多因素耦合对RC梁抗弯承载力的影响及预测方法。Liu等利用等效爆火时间作为损伤预测指标,以结构模态信息为输入参数,建立了一种基于支持向量机(SVM)的损伤识别模型,进而提出了面向连续梁火灾损伤的三步定位方法[6]。许文龙建立了火灾下RC梁数值分析模型,分析了不同受火时间下混凝土爆裂对温度场及抗弯承载力的影响,指出混凝土爆裂深度对截面温度场及抗弯承载力影响最大[7]。Behnam采用数值模型对比分析混凝土爆裂对结构性能的影响,指出混凝土爆裂会较快地导致结构性能劣化[8]。王富强采用数值模型分析了火灾后柱式桥墩的残余极限承载力,提出了考虑混凝土爆裂的RC柱式桥墩残余极限承载力计算公式[9]。Kodur等利用数值分析和试验测试证实了钢筋/混凝土界面黏结性能退化对RC梁承载能力及挠度具有较大影响,数值模拟过程中需要考虑高温后界面粘结本构关系[1]。郭梓栋等采用ANSYS建立数值模型,计算不同火灾工况下的抗弯承载力,分析了T梁承载能力的变化规律,提出了T梁抗弯承载力计算的修正公式[10]。

因此,针对火灾对构件影响的不确定性,本文建立RC梁高温数值分析模型,构建由受火时间、爆裂特征与抗弯承载力的样本数据,提出火灾后RC梁残余抗弯承载力的多元回归和SVM预测方法,为快速计算火灾高温后RC梁抗弯承载力提供方法支撑。

1 数值分析模型构建

1.1 构件尺寸

以文献[2]中进行火灾试验的RC梁为研究对象,建立RC梁的数值分析模型。构件的几何尺寸及配筋布置如图1所示。梁总长为3 000 mm,截面尺寸为250 mm×400 mm,左端为固定铰支座,右端为可动铰支座。RC梁的跨中截面和靠近固定铰支座1/3跨截面处布置6个热电偶;采用ISO 834国际火灾标准升温曲线开展火灾升温试验,升温至120 min之后停火,并冷却至室温后进行静载试验。

a—梁截面尺寸; b—配筋示意; c—热电偶布置。

1.2 模型构建

本文利用ABAQUS软件,采用顺序耦合分析法对高温后RC梁抗弯承载力进行分析,数值分析模型构建及模拟过程:1)对RC梁进行标准升温传热分析,获得不同截面温度场。混凝土采用DC3D8单元,钢筋采用DC1D2单元,钢筋和混凝土之间选用tie约束。初始温度设置为20 ℃,斯蒂芬玻尔兹曼常量以分钟为单位时的取值为3.402×10-6J/(m2·min·K4),绝对零度取-273.15 ℃;RC梁三面受火(底面和两个侧面),梁体顶面和梁端至支座100 mm范围不受火,辐射换热系数取0.8,受火面的对流换热系数取2 100 J/(m2·min·℃),非受火面的对流换热系数取600 J/(m2·min·℃)。2)确定不同材料高温后的力学性能,模拟考虑混凝土爆裂的RC梁的力学行为。混凝土采用C3D8R单元,钢筋采用T3D2单元,钢筋与混凝土黏结滑移行为采用非线性弹簧单元模拟[1,11];解除纵向钢筋与混凝土间的嵌入式约束关系,在钢筋和混凝土节点处添加三向节点弹簧。假定箍筋与混凝土之间黏结良好。数值模型的节点编号、网格尺寸与温度场分析时保持一致。3)混凝土高温爆裂采用“生死单元”来模拟,统一设定在升温后第15分钟发生混凝土爆裂。a.切分出混凝土爆裂工况,创建混凝土爆裂单元集合;b.设置混凝土爆裂前/后的升温时间;c.在相互作用模块杀死发生爆裂的混凝土单元,对新受火面则重新设置边界条件。

1.3 参数设置

试验炉内RC梁在升温过程中属于瞬态传热过程,一般由热传导、热对流和热辐射方式任意组合传递热能。数值模型中的材料参数和本构关系为:混凝土密度ρc=2 500 kg/m3,比热容Cc=921.14 J/(kg·℃),热传导系数λc、热膨胀系数αc随温度变化关系式见文献[2,11];钢筋密度ρs=7 800 kg/m3,比热容Cs、热传导系数λs和热膨胀系数αs随温度变化关系式见文献[2,11-12]。本构关系[13]分别采用耦合材料高温退化效应的混凝土塑性损伤模型、二折线弹塑性模型,高温后混凝土强度、弹性模量退化关系见文献[2,13],钢筋强度、弹性模型高温退化关系见文献[2,14],混凝土和钢筋的泊松比分别为0.2,0.3。

另外,火灾高温下混凝土构件中的钢筋与混凝土的界面黏结性能将会退化,采用文献[11]中带肋钢筋高温黏结滑移退化关系模拟;局部黏结滑移关系采用CEB-FIP1990中的模型。火灾试验过程中由于试验设备及操作技术等因素影响,火灾试验实际升温曲线与标准升温曲线ISO-834存在差异。本文采用等效爆火时间[15]作为数值模拟输入参数,转换式如下:

(1)

式中:te为等效爆火时间;f为受火时间;Tgm和T0分别为炉内气体温度的最大值和初始值。

2 数值分析模型验证

构件截面温度场是进行高温后抗弯承载力计算的基础,因此以温度场和抗弯承载力作对比以验证该数值模型的有效性,将构件1—1截面的温度场试验值与模拟值对比,如图2所示。

a—测点1～3; b—测点4、5。

通过测点温度曲线对比可知,模拟温度曲线较为平滑,未出现温度平台现象,但整体升温趋势及120 min时的温度与试验实测值较为接近(由于测点6失效,这里未列出对比数值);部分测点最终温度值两者不完全相同,可能是受测点绑扎位置误差、试验炉温升曲线影响,但大体趋势表明该数值模型是有效可靠的。另外,基于模拟的截面温度场,采用等效截面法[13]计算试验梁的火灾后抗弯承载力(CV),并与试验实测值(TV)、数值模拟值(SV)(结合火灾试验确定梁的跨中底面1 m范围发生爆裂,爆裂深度为混凝土保护层的1/2,即15 mm)对比如图3。

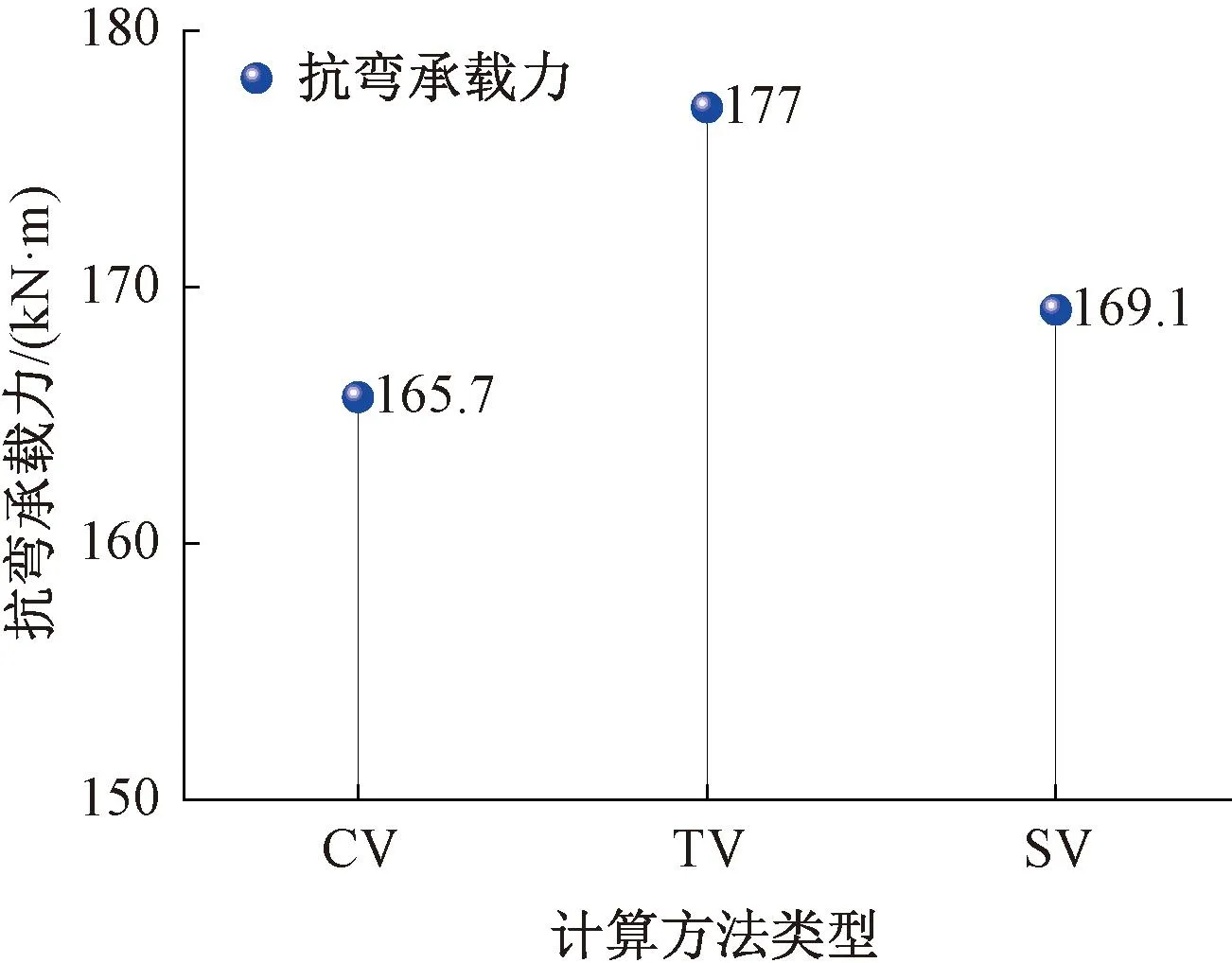
图3 抗弯承载力值对比

火灾后抗弯承载力的理论计算值、数值模拟值均小于试验实测值,但相对误差分别为6.38%、4.46%,表明了采用该数值模型开展火灾高温后RC梁的抗弯承载力计算是可行的。

3 抗弯承载力预测方法

3.1 样本数据库建立

考虑受火时间(t)、爆裂深度(h)和爆裂面积比(s)三个因素对RC梁火灾后抗弯承载力的影响,结合RC梁火灾试验与数值分析模型,设定混凝土爆裂仅发生在梁的跨中1 m范围内,受火时间为30,60,90,120,150 min;爆裂深度为5,10,15,20,25 mm;爆裂面积比为10%、16%、23%、29%、42%、55%、68%、80%、90%、100%。采用交叉组合方法,共计形成250组数值模拟工况参数,利用构建的数值分析模型计算其残余抗弯承载力MT,从而构建250个样本数据库。

3.2 多元回归分析法

采用统计分析软件SPSS回归拟合得到火灾后RC梁残余抗弯承载力的衰减系数k:

k=MT/M0

(2)

式中:MT为不同受火时间下RC梁的残余抗弯承载力;M0为RC梁的初始抗弯承载力,理论计算值为213.2 kN·m。

3个关键影响因素与抗弯承载力之间的线性拟合关系式为:

(3)

式中:决定系数R2=0.944;t为试验梁的受火时间,min;h为混凝土爆裂深度,mm;s为混凝土爆裂面积比,%。

3.3 SVM的预测方法

由于多元回归分析方法存在泛化能力弱、主观能力强等缺点,引入机器学习方法可以有效解决这类非线性、高维度的高温后RC梁残余抗弯承载力预测问题。支持向量机(SVM)方法是基于统计学习理论的一种机器学习方法,通过给定的训练样本集Y={(xi,yi)},通过非线性映射φ(x),将输入向量x映射到高维空间,用函数f(x)=ωφ(x)+b对数据进行拟合,并寻找最优参数ω和b使f(x)逼近y。通过K(xi,xj)=φ(xi)φ(xj)实现从低维到高维的转换,避免非线性映射函数φ(x)的解,降低计算时间和复杂度。本文采用高斯径向基函数:

K(xi,xj)=exp(-γ‖xi-xj‖2)

(4)

式中:γ为核函数(γ>0);‖xi-xj‖2为欧几里得范数。此外,选取决定系数(R2)和均方差(MSR)表示相关性及训练误差情况,以评估SVM模型的预测能力。R2越接近于1,则拟合回归的效果越好;MSR的值越小,则预测模型越精确。

(5a)

(5b)

采用250个数值模拟工况样本,迭代计算训练构建SVM预测模型,模型训练效果见图4。相关系数和均方误差分别为:R2=9.962,MSE=0.494 76。本模型的残差范围在(-5～5)之间。由响应关系可以发现,绝大多数数值接近完美预测线,预测结果与真实值间的误差较小,模型预测效果良好。

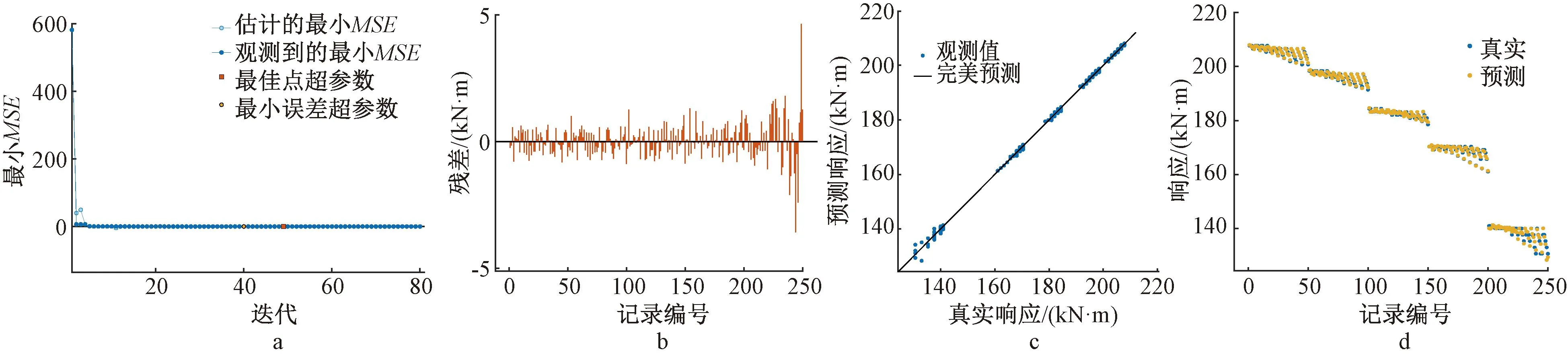
a—最小均方差变化; b—不同工况下的残差情况; c—训练模型的预测能力; d—真实值与预测值比较。

为了检验SVM预测模型的泛化性能,设定受火时间分别为50、80、110和140 min,对应的爆裂面积比分别为35%、48%、75%和93%,变化爆裂深度取值,组合形成检验样本数据库,运用训练后的SVM模型和多元回归方法计算样本的残余抗弯承载力,并与数值模拟值进行对比,结果见表1。可见:火灾后RC梁的抗弯承载力的SVM预测值与模拟值的相对误差在0.05%～4.05%之间,平均相对误差为1.88%;多元回归预测值与数值模拟值的相对误差在0.65%～7.41%之间,平均相对误差为2.64%。可见,两种预测方法的预测相对误差均在10%以内,但基于机器学习的SVM预测方法更加精确,可用于RC梁火灾后残余抗弯承载力的预测。

表1 抗弯承载力预测值与模拟值对比

4 结 论

建立了火灾作用下RC梁数值分析模型,并用火灾试验验证了模型有效性;选取受火时间、爆裂深度和爆裂面积比为关键特征参数,交叉组合设计了250组数值模拟工况,并利用数值模型计算其抗弯承载力,构建了回归分析和机器学习所需的样本数据集,建立了基于回归分析和SVM的RC梁火灾后残余抗弯承载力预测模型,并与数值模拟结果进行了预测精度分析,得出如下结论:

1)分别从温度场和抗弯承载力两方面验证了RC数值分析模型的有效性。数值模拟的升温趋势及120 min时的温度与试验实测值较为接近;火灾后RC梁抗弯承载力的理论计算值、数值模拟值均小于试验实测值,但相对误差分别为6.38%、4.46%。

2)火灾后RC梁的残余抗弯承载力的SVM预测值、多元回归预测值与数值模拟值的平均相对误差分别为1.88%和 2.64%,均小于10%,表明两种方法均可满足工程应用,但SVM预测结果更加准确。

3)该预测模型可以用于RC梁火灾后残余抗弯 承载力预测,但后续研究可以通过扩充数据集和关键影响参数来不断丰富该模型,且进一步在工程实践中进行应用验证,为RC梁火灾后抗弯承载力提供方法支撑和技术参考。