不同支撑形式铰接钢框架结构抗震性能试验研究*

李 然 舒赣平 胡 波 陈士通

(1.石家庄铁道大学土木工程学院, 石家庄 050043; 2.河北省交通应急保障技术创新中心, 石家庄 050043; 3.东南大学土木工程学院, 南京 211189; 4.石家庄铁道大学工程力学系, 石家庄 050043)

0 引 言

钢框架-支撑结构体系在水平外力作用下,支撑作为第一道防线承担水平荷载,支撑体系破坏后,水平荷载转向由梁柱承担,支撑部分破坏后结构的抗侧刚度将大大降低,刚度及耗能性能急剧下降,且延性较差,会进一步使破坏转向梁柱。将传统钢框架-支撑结构体系的连接设计成铰接,使梁柱主要承受竖向荷载,支撑主要承受水平荷载,罕遇地震下,框架的梁柱保持弹性,结构塑性变形主要集中于支撑部分。如果在铰接钢框架-支撑结构体系中采用具有耗能和自复位功能的支撑,地震作用下,耗能自复位支撑将消耗地震能量起到保护结构的作用,震后,支撑的自复位功能又能使结构回复到其初始状态或仅留下很小的残余变形,利于震后结构的修复与重新使用。

自复位耗能支撑一般由耗能系统、复位系统及约束连接系统组合而成。耗能系统可耗散外部输入的地震能量,保护主体结构;复位系统可以减少或消除主体结构的残余变形,其概念是由Christopoulos和Tremblay[1-2]首次提出的。之后,很多学者致力于自复位耗能支撑的研究[3-6],然而,受材料弹性变形的限制,多数支撑不能满足结构大变形的需求。形状记忆合金(SMA)的最大可恢复应变达7%以上,是理想的复位材料,因此,很多学者将SMA材料作为复位材料应用于自复位耗能支撑,并取得了理想的效果[7-13]。随着研究的深入,广大研究者设计的SMA自复位耗能支撑基本可分为两类:SMA与其他材料复合而成的支撑;单纯由SMA作为耗能和自复位材料的支撑。

随着性能化抗震设计要求的提出,耗能且兼具复位功能的支撑成为当前的主流。为此,基于SMA的各项性能,将研发的SMA自复位耗能装置嵌入铰接钢框架-支撑结构体系,并通过试验将其与普通钢框架-支撑结构体系进行对比,并对试验过程、现象和结果进行分析和探讨。

1 SMA自复位耗能装置(SMAD)

试验所用自复位耗能装置(SMAD)主要由外筒、端板、中间板、拉压杆和核心SMA丝束等组成,其构造示意如图1所示。核心SMA丝束通过中间板上的开孔缠绕在两中间板之间并用U形卡进行锚固,外筒各段通过螺纹环环相扣。

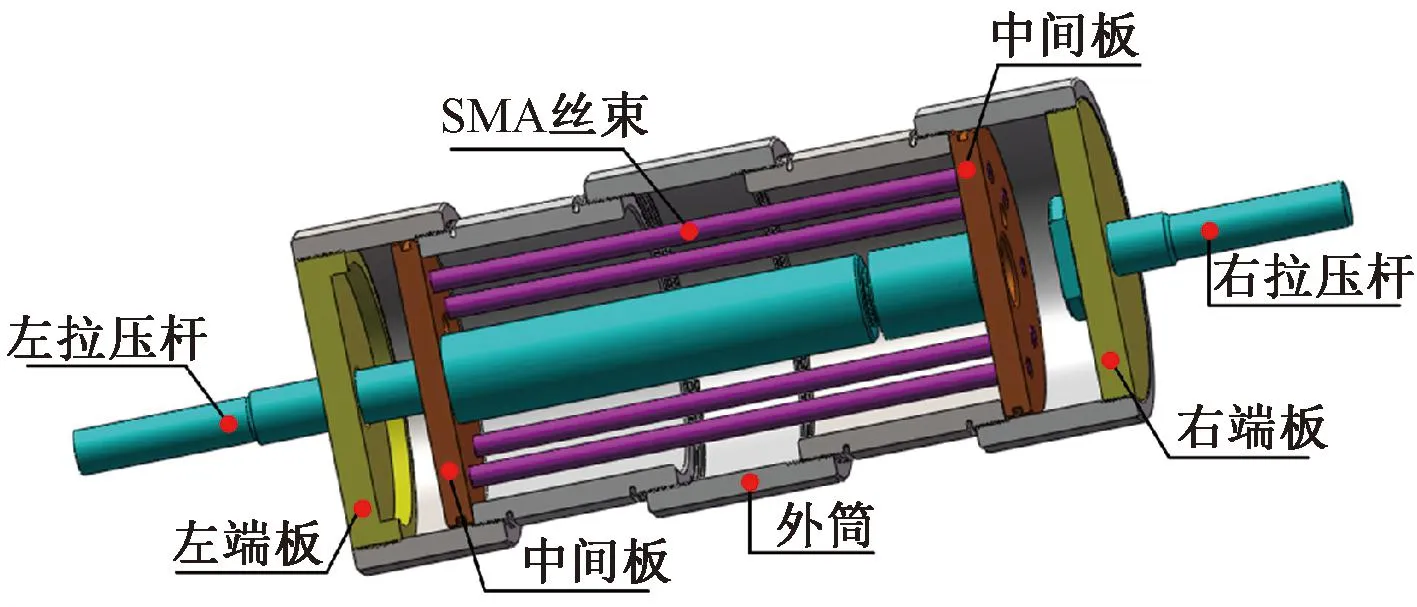
图1 自复位耗能装置构造

2 模型设计

2.1 模型概况

设计制作了两榀跨度L=6 m,层高H=3 m的铰接钢框架-支撑子结构,其中一榀为单跨双层铰接钢框架-普通支撑子结构,另一榀为单跨双层铰接钢框架-自复位耗能支撑子结构。子结构的概念模型如图2所示。

图2 铰接钢框架-支撑子结构概念模型 m

2.2 材料性能

结构梁、柱采用焊接H型钢,支撑采用热轧无缝钢管,普通支撑采用Q235,其余构件均采用Q345,各部分材料性能如表1所示。

表1 框架材料性能

自复位耗能装置核心部分采用Ni-Ti SMA丝,其应力-应变关系曲线见图3,图中,EA、EM分别为SMA丝的奥氏体和马氏体弹性模量;σMs、σMf分别为SMA丝的马氏体相变开始应力、完成应力;σAs、σAf分别为奥氏体相变开始应力、完成应力;εL为最大相变应变,相关性能参数值列于表2。设计时应保证装置其他构件处于弹性状态。

表2 SMA丝材料性能

图3 SMA丝应力-应变曲线

2.3 构件设计

2.3.1设计准则

结构设计时主要遵循以下原则:

1)铰接钢框架-普通支撑钢框架子结构中支撑的破坏应不迟于梁柱破坏;

2)两榀铰接钢框架-支撑子结构应具有相同的屈服承载力,且结构屈服时达到结构的弹性层间位移角限值;

3)铰接钢框架-自复位耗能支撑子结构超出弹性位移角但未超出弹塑性位移角限值时,自复位耗能装置发挥耗能作用消耗地震能量,卸载后结构残余变形减小甚至消失。

2.3.2铰接钢框架-普通支撑子结构(FMB)

根据试验室设备及场地条件,将原框架结构进行1∶2缩尺设计,按照GB 50009—2012《建筑结构荷载规范》[14]的规定,考虑并分析各种荷载组合,确定最不利荷载组合为1.2SG+1.4SQ,其中SG为永久荷载作用效应设计值,SQ为可变荷载作用效应设计值。将组合后的荷载简化为柱顶集中荷载,经计算,每个柱顶分别施加410.4 kN的集中荷载。

根据轴压比计算公式(n=N/Ncr)可知,施加于钢柱的轴压比为0.334。经设计,两铰接支撑框架结构各构件截面如表3所示。

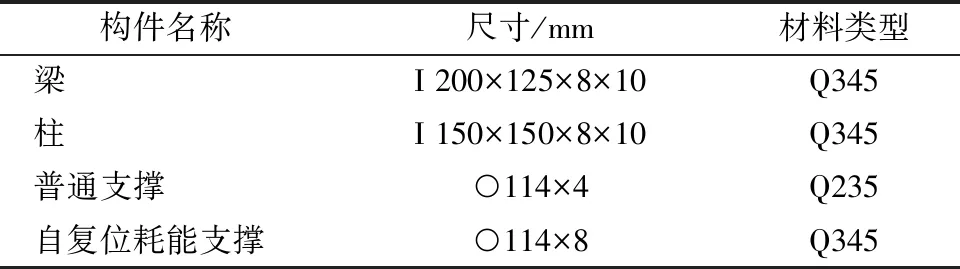
表3 框架结构构件截面尺寸

2.3.3铰接钢框架-自复位耗能支撑子结构(FMD)

如图4所示,将单榀单跨单层支撑框架构成的整体称为一个基本结构单元,其中自复位耗能支撑由自复位耗能装置和普通支撑段两部分串联而成,普通支撑铰接钢框架的支撑部分仅由普通支撑构成。

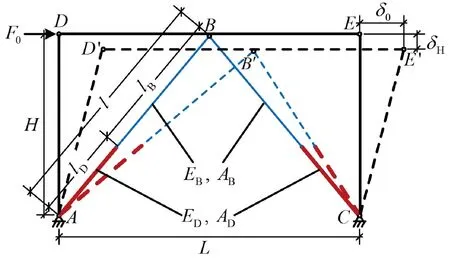
图4 基本结构单元受力变形示意

设一个自复位耗能支撑的总长度为l,则有以下几何关系:

l=lD+lB

(1a)

定义长度比:

αl=lD/l

(1b)

刚度比:

αEA=EDAD/(EBAB)

(1c)

式中:EB、AB和lB分别为普通支撑段的弹性模量、初始面积和初始长度;ED、AD和lD分别为自复位耗能装置的弹性模量、核心SMA丝束面积和初始长度。

设一个自复位耗能支撑的等效刚度为EeqAeq,则有:

EeqAeq=EDAD/c1

(2)

其中c1=(1-αl)αEA+αl

式中:Eeq为等效弹性模量;Aeq为等效面积。

自复位耗能系统发生水平位移δ0时轴向长度变化为:

(3)

自复位耗能体系的侧向刚度K0可表示如下:

(4)

经设计,取自复位耗能装置核心SMA丝束长度lSMA=300 mm,面积ASMA=780 mm2,装置其他构件根据构造措施进行设计,支撑段材料相关参数见表1。

3 试验概况

3.1 试验装置

以铰接钢框架-自复位耗能支撑子结构为例,其总体装配如图5所示,一、二层分别采用50 t 201.45型和150 t 201.70型液压伺服作动器,并采用柱内预应力的方式模拟柱顶荷载。为防止框架面外失稳,采用四个柱侧向支撑和两个梁侧向支撑对其面外位移进行约束。

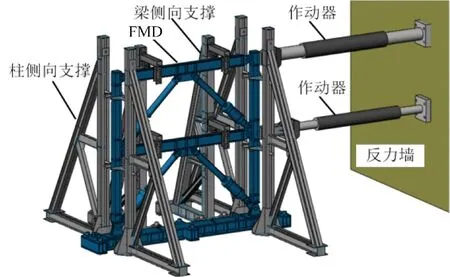
图5 试验总体装配示意

3.2 加载制度及测量系统

采用两台液压伺服作动器联动加载的位移-力混合控制进行加载,二层作动器为主动控制作动器,采用位移控制;一层作动器为被动控制作动器,采用力控制,其荷载值为二层作动器荷载值的1/20,根据底部剪力法基本原理,该加载模式可模拟六层结构的水平荷载分布。对上下层框架同步、分级加载,二层作动器的加载历程如图6所示,幅值0～40 mm为弹性阶段,40～80 mm为耗能阶段。

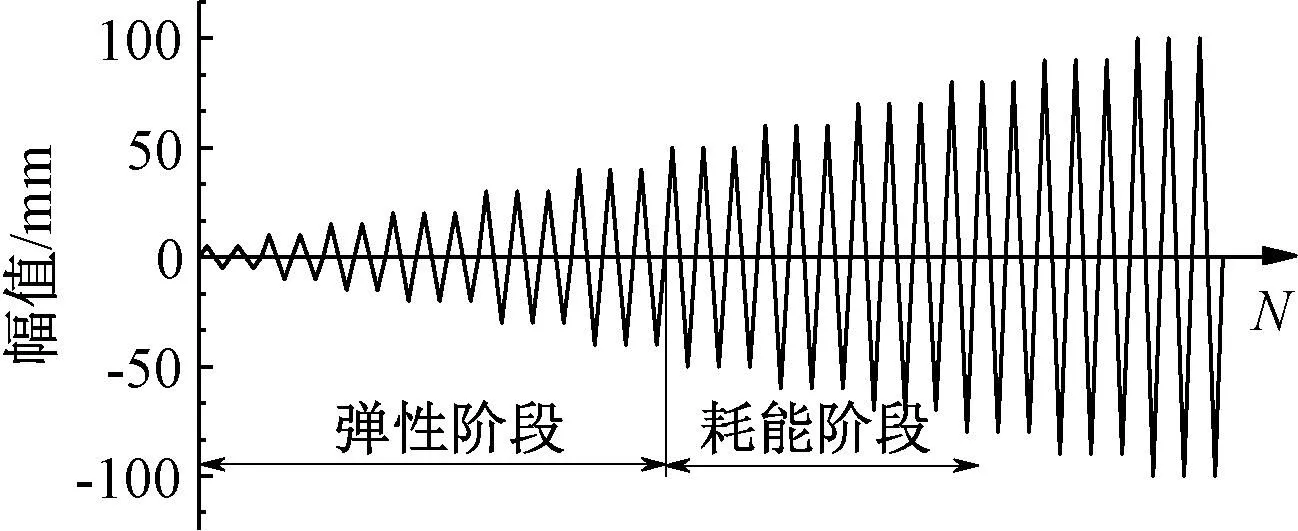
图6 加载历程

利用位移传感器、应变片、应变花及数字图像处理(DIP)技术对结构梁、柱、支撑等的位移、应力、变形等进行测量,测点布置如图7所示。

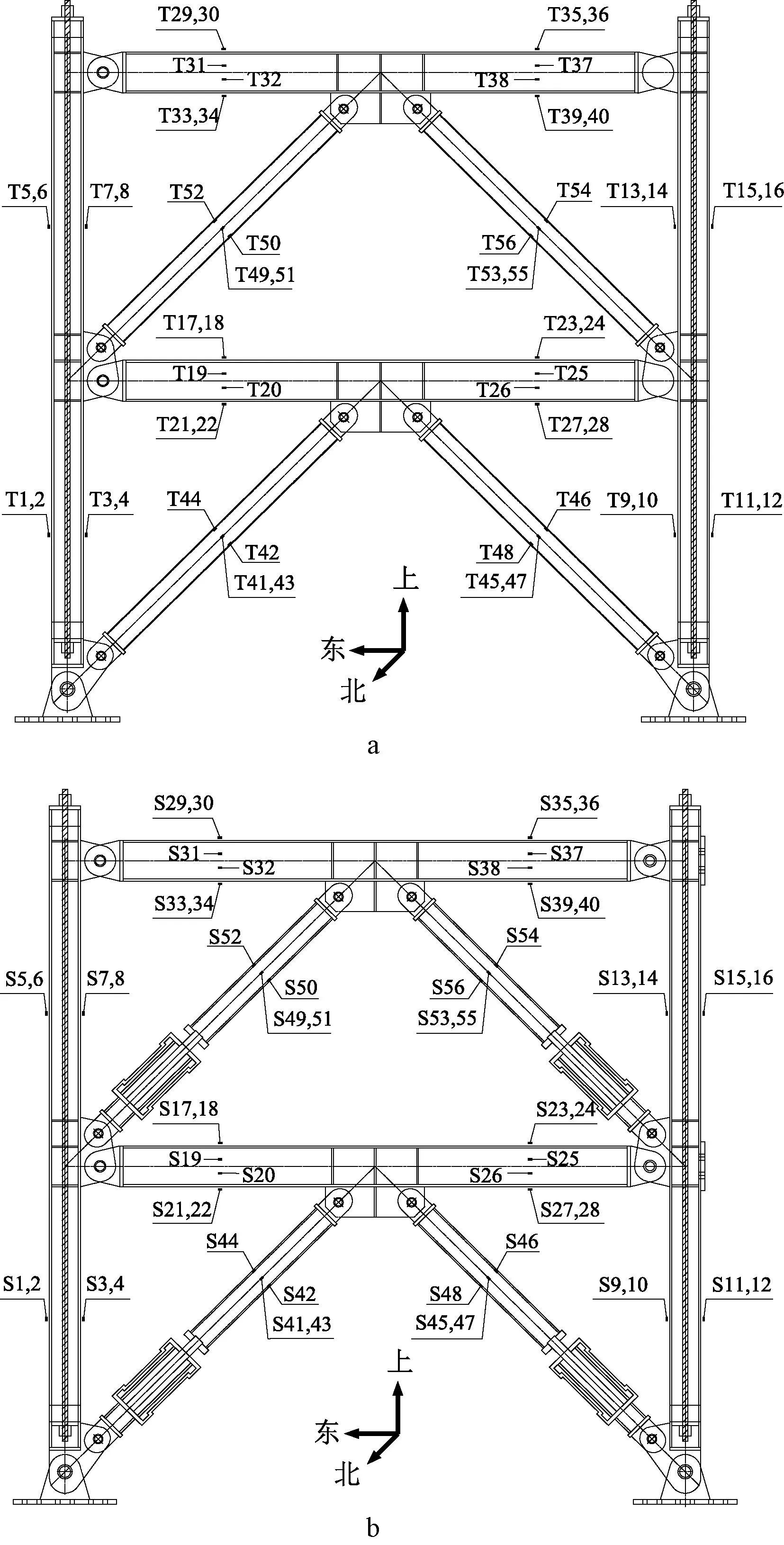
a—普通支撑铰接钢框架; b—自复位耗能支撑铰接钢框架。

4 试验现象与结果

为便于描述,规定加载方向以推为正,以拉为负,以下分别介绍两榀钢框架的试验情况。

4.1 试验现象

4.1.1铰接钢框架-普通支撑子结构(FMB)

试验弹性阶段,框架无明显破坏现象,在该阶段的0～10 mm幅值范围内,结构的刚度较小,之后荷载-位移曲线呈线性增长;加载幅值40 mm时结构二层正负向承载力分别达到了505.5 kN和524.7 kN。

试验耗能阶段,第一次循环加载至42.8 mm时结构出现刚度退化,位移增大至45.2 mm时,承载力达到最大值535.2 kN,之后承载力突然下降至432.9 kN,二层东侧支撑发生面内整体失稳(图8a),卸载后反向加载,位移刚达到40 mm结构即开始屈服,二层西侧支撑发生面外失稳(图9a),该加载过程中,最大承载力仅比弹性阶段增长了3.4%;第二次循环正向加载,二层东侧支撑出现凹陷并有明显折痕(图8b),二层梁出现明显下挠并有局部翘曲,负向加载时,二层西侧支撑中部出现凹陷(图9b),东侧支撑涂漆剥落;加载至第三次循环正负向50 mm时,承载力已分别下降至328.1 kN和461.6 kN,此时,结构正负向承载力分别下降至第一次循环正负向最大承载力的75.8%和85.1%,基本可认为结构已破坏,东侧支撑发生撕裂(图8c),西侧支撑鼓曲不可恢复。FMB的荷载-位移曲线如图10所示。

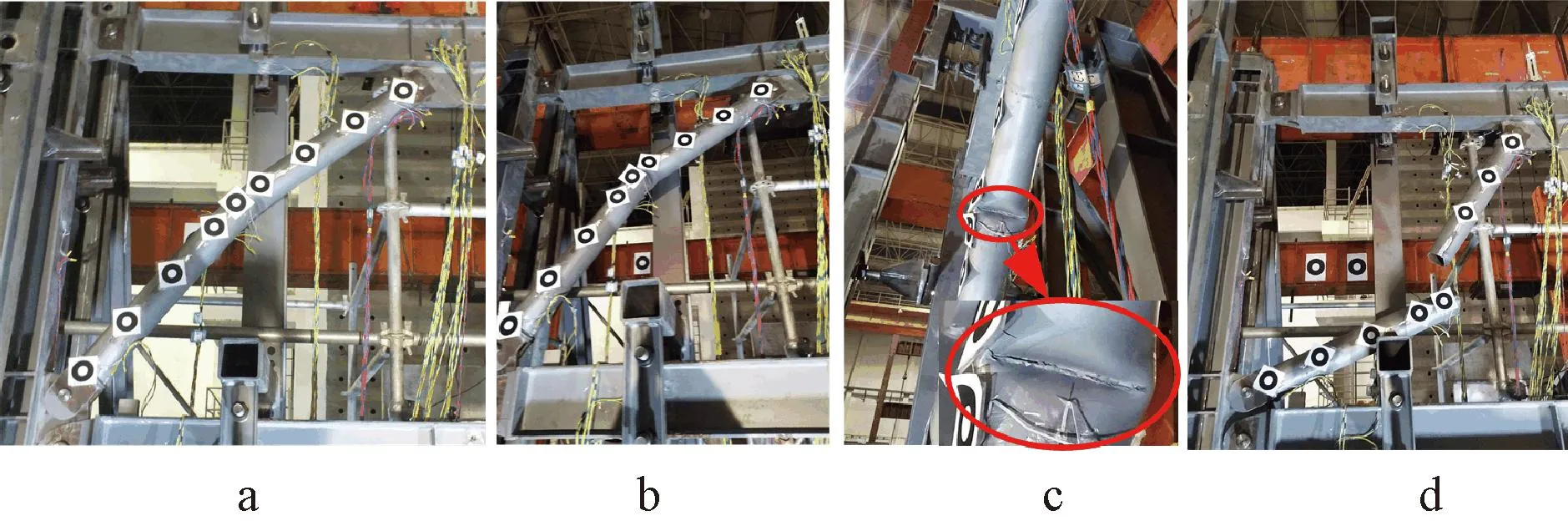
a—整体失稳; b—局部凹陷; c—撕裂; d—断裂。

a—整体失稳; b—局部凹陷。

图10 框架荷载-位移曲线

为进一步观察结构破坏现象,对其进行了下一级加载,正向60 mm位移时承载力较50 mm时基本无变化,卸载时二层东侧支撑撕裂进一步扩大,负向加载至55 mm时,结构发出巨大声响,二层东侧支撑被全部拉断(图8d),完全失去承载能力,结构承载力急剧下降至163.8 kN,试验终止。

4.1.2铰接钢框架-自复位耗能支撑子结构(FMD)

自复位耗能支撑中自复位耗能装置段的刚度远小于支撑段刚度,加载过程中支撑的变形主要发生在装置段,装置拉伸前后情况如图11所示。

a—东侧阻尼器; b—西侧阻尼器。

弹性加载阶段,结构的承载力基本呈弹性增长;在耗能阶段,当加载幅值超过40 mm时,结构刚度开始变小,整个加载过程中结构承载力缓慢增长,且未发现结构破坏;受柱侧向支撑顶杆长度所限,负向加载至-80 mm时柱翼缘已基本与侧向支撑顶杆端部接触,为确保试验设备的安全,至最大幅值80 mm时加载结束,框架最大承载力达到651.2 kN。FMD的荷载-位移曲线见图10。

4.2 试验结果

4.2.1位 移

试验过程中,随着加载幅值的增大,两结构二层柱顶水平位移呈线性增长,如图12a所示,这与试验加载制度符合;位移幅值大于40 mm时,FMB结构由于二层支撑的破坏导致结构二层承载力降低,进而一层位移幅值有所减小;而FMD结构整个加载过程未发生破坏,结构柱水平位移始终保持线性增长。

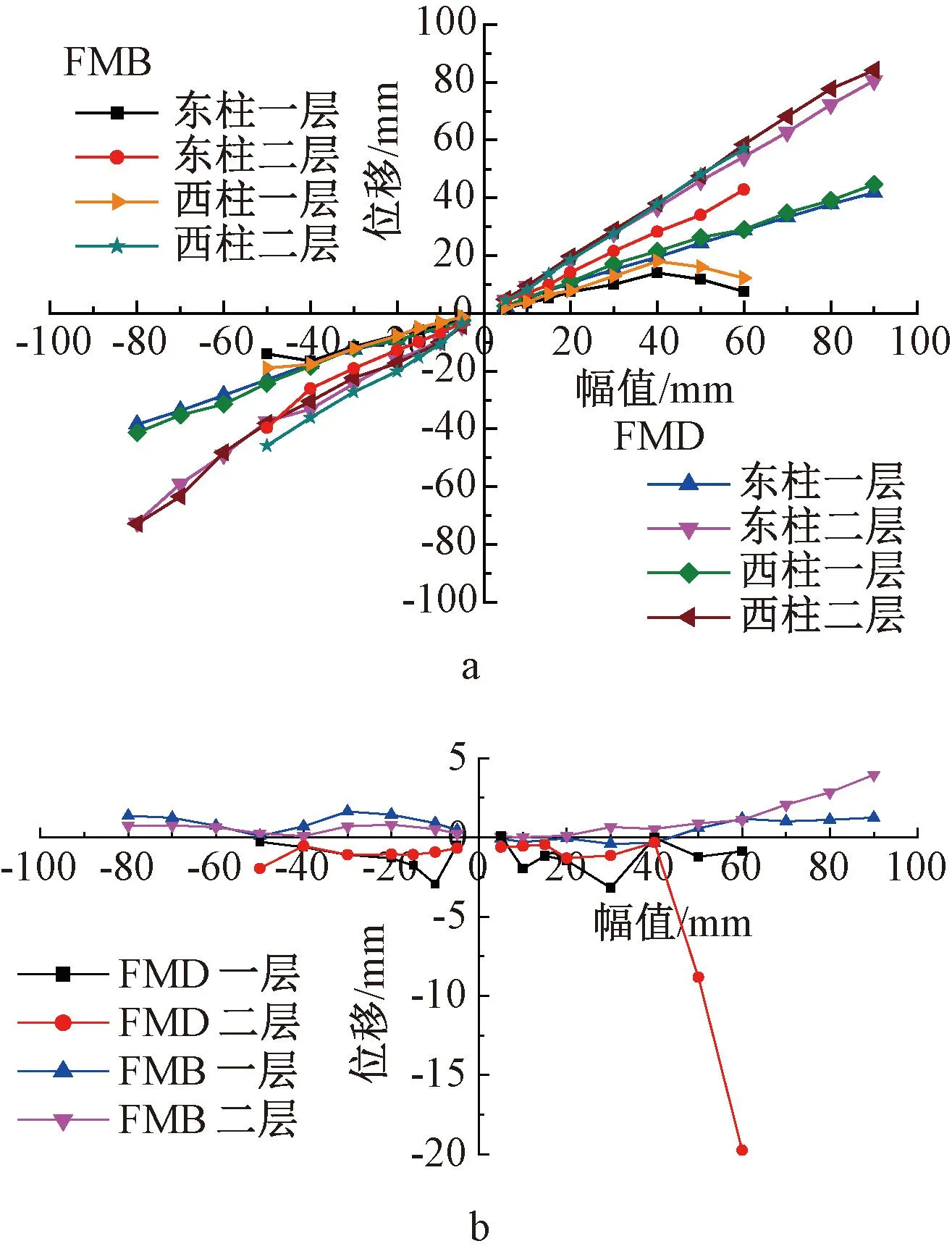
a—框架柱顶水平位移; b—框架梁竖向位移。

图12b为框架梁竖向位移情况,加载幅值小于40 mm时两结构框架梁的竖向位移变化不大,加载幅值由40 mm增大至50 mm时FMB结构由于二层支撑发生破坏,二层梁竖向变形突然增大,至60 mm时变形进一步增大至20 mm;FMD结构竖向位移有逐渐增大的趋势,但最大变形量不超过5 mm。

4.2.2应 变

FMB和FMD结构梁、柱在加载过程中均处于弹性状态,两结构梁最大应变分别发生在二层梁东侧上翼缘及二层西侧腹板,最大应变分别为1 493×10-6和974×10-6;FMB和FMD结构柱最大应变分别为1 820×10-6和574×10-6,均处于弹性状态。

图13给出了FMB和FMD结构加载过程中支撑跨中的应变变化曲线。由图13a、图13b可见,加载幅值不大于40 mm时FMB结构的支撑应变呈线性增长,且最大应变不超过2 000×10-6,处于弹性状态;加载幅值超过40 mm后除一层西侧支撑应变呈线性增长外,其余3个支撑屈服,应变发生突变;对于FMD结构(图13c、图13d),加载幅值不大于40 mm时,支撑应变同样呈线性增长,在40 mm幅值附近,应变值增长速率有所减缓,这与结构在40 mm幅值时刚度变小趋势一致,整个加载过程中支撑应变约1 000×10-6,始终处于弹性状态。

a—T41～T48; b—T49～T56; c—S41～S48; d—S49～S56。

5 结果对比

选取特征值Qmax、Δmax、Qy、Δy、Δu、K0、θmax对不同支撑形式的框架-支撑结构各项性能进行描述。其中Qmax、Δmax分别为框架的最大剪力及其对应的层位移;Qy、Δy分别为框架屈服剪力及其对应的层

位移;Δu为框架剪力降至0.85的最大剪力时对应的层位移,μ=Δu/Δy为框架的延性系数,K0为框架的初始刚度,θmax为框架二层的最大层间位移角。

图14和表4分别为两框架结构二层的水平剪力-位移骨架曲线和抗震性能特征值,其中骨架曲线中的水平位移为框架二层梁端相对地面的水平位移。

表4 框架二层抗震性能特征值

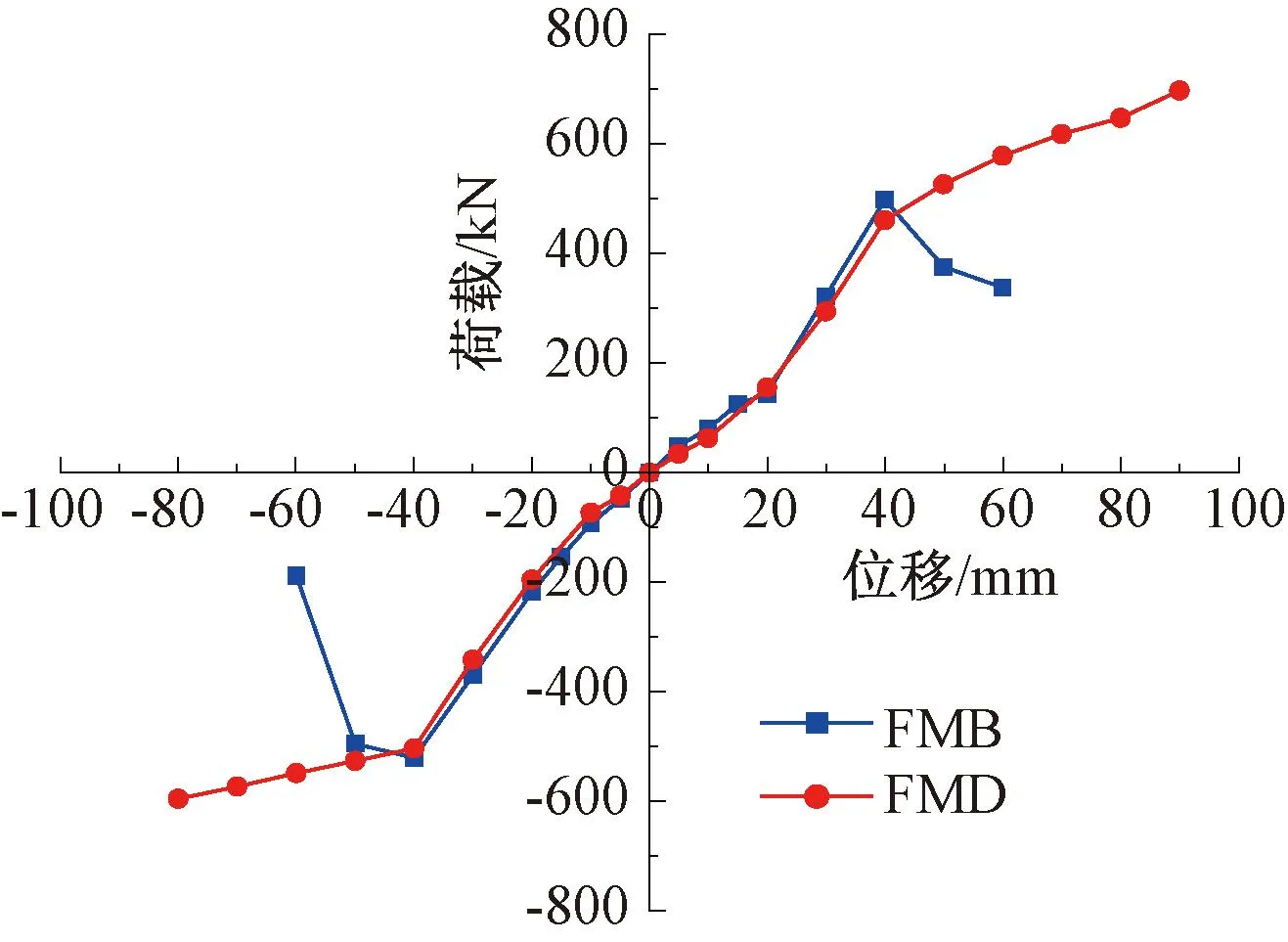
图14 水平剪力-位移骨架曲线

5.1 屈服荷载及承载力

由图14和表4可见,FMB正负加载方向的屈服荷载分别为436.6 kN和467.7 kN,具有一定的不对称性,屈服荷载约为最大承载力的88%,框架达到最大承载力后,出现明显的下降段,并迅速降低至结构破坏。

FMD正负加载方向的屈服承载力分别为517.5 kN和514.9 kN,两者基本相等;框架达到屈服承载力后,刚度明显降低,但承载力仍在继续增长,这与阻尼器核心SMA丝束的性能一致,整个加载过程尚未达到结构的最大承载力。

对比两结构可见,FMD的承载力远高于FMB的最大承载力,且在试验设备及其装置加载能力范围内未达到其最大承载力;由于加载时试验大厅温度很高,装置核心SMA丝束的各特征荷载较设计时有所提高,导致FMD的屈服荷载大于FMB的屈服荷载。

5.2 延 性

由表4可见,FMB在正、负向加载状态下的延性系数和层间位移角分别为1.03、1.23和1/70.2、1/64.2;对于FMD来说,由于加载结束时结构尚未发生破坏,其实际正、负向加载时的延性系数和层间位移角将分别大于2.13、2.06和1/34.6、1/36.5。对比可见,FMD的延性要优于FMB的延性,即前者的抗震性能优于后者。

5.3 耗能及复位性能

FMB的支撑部分在水平荷载作用下发生了面外失稳,之后很快就发生了破坏,耗能性能差,且由于支撑的屈曲和失稳甚至破坏,卸载后结构不能自行复位,支撑无法修复;除SMAD外,FMD其余各部分在水平荷载作用下始终处于弹性状态,SMAD能消耗部分地震能量,且FMD在外荷载移除后可复位至其初始位置,期间并未发生结构的破坏,无需进行结构修复。因此,FMD的耗能和复位性能要优于FMB。

6 结 论

对一榀铰接钢框架-普通支撑子结构与一榀铰接钢框架-自复位耗能支撑子结构的抗震性能进行了研究和对比分析,可得到如下结论:

1)铰接钢框架-普通支撑子结构在水平荷载作用下,二层支撑首先发生面外失稳和屈曲破坏,之后一层支撑面外位移有所增大;随着加载幅值的增大,二层梁-支撑节点域梁的上翼缘开始出现微小翘曲;整个加载过程中,梁、柱始终处于弹性状态。

2)铰接钢框架-自复位耗能支撑子结构在水平荷载作用下至加载幅值80 mm时仍未发生破坏,梁、柱始终处于弹性状态。

3)铰接钢框架-自复位耗能支撑子结构的延性系数为铰接钢框架-普通支撑子结构的2倍以上,且具有较高的承载力和层间位移角。

4)由于增设了自复位耗能装置,铰接钢框架-自复位耗能支撑子结构的耗能性能和复位性能均优于铰接钢框架-普通支撑子结构。