需求波动、竞争强度对供应链主导权力优势的影响研究

何 征，蒋 雪，冯 春

(西南交通大学 交通运输与物流学院，四川 成都 610031)

据El-Ansary 等[1]的定义，供应链成员的权力是其控制供应链其他成员决策变量的能力。而通过供应链博弈中的博弈时序可以间接地表达供应链结构权力的差异[2-3]。博弈中率先决策者会影响后决策者的决策，从而形成其主导权。在这个框架下，不少研究者关注主导权力对供应链绩效的影响，例如Shi 等[4]、Wang 等[5]和Chen[6]等。而这些研究大多是基于“1 对1” (一个供应商和一个零售商) 的供应链结构。并且认为供应链的主导权力影响着供应链成员的利润分配比例。具有市场主导权力的一方能获得更多的利润份额。因此供应链中，企业会因为争夺主导权力而增加投入。随着全球化的普遍推进和电商的飞速发展，由多个供应商通过线上直销或线下批发等渠道为多个零售商提供产品所形成的“多对多”模式十分流行。与“1 对1”供应链的最大区别在于，“多对多”模式引入了供应商/零售商之间的水平竞争。那么，水平竞争是否会破环主导权力的利润优势呢？或者说水平竞争激烈下，公司是否还会愿意增加投入以争夺市场主导权力是本文研究的动机之一。

此外，很多研究供应链结构权力的文献是基于如下现实：一些零售巨头在批发价格上不断压制供应商，这种强大的市场权力可能还会影响消费者福利。但是，一方主导权力向另一方转换是一个逐步变化的过程，不是一开始就掌握了主导权力。现实中，非主导一方可能会首先通过一些方式削弱主导方的权力优势，例如Korpeoglu 等[7]提出，零售商可以通过改变决策变量 (以采购预算作为决策变量)来影响批发价格，以行使自己的买方权力，获取更高的利润水平。Geylani 等[8]开发了一个理论模型，以展示制造商如何战略性地应对占主导地位的零售商。这些情况下，从决策时序来看，主导方并未失去主导权，但非主导方却通过某些技术削弱了主导方的权力优势。而随着非主导方的不断发展壮大，其权力得以进一步提升，形成与主导方势均力敌的局面。因此，在目前的研究中，对于主导权力逐渐降低的现实情况的模拟还有待进一步挖掘。

基于上述理论和实践动机，本文意将对结构权力优势的探讨拓展到“多对多”的供应系统中，具体研究以下几个问题。1) 在多对多的供应链系统中，供应链主导权力是否仍然意味着更高的利润比例？供应商主导权力的逐渐削弱对供应链和公司绩效产生怎样的影响？2) 需求波动、供应链竞争强度等外部市场因素是如何干扰主导权力优势的？3) 什么情况下，参与者应该努力争夺市场权力？什么情况下，参与者不必过分在意市场权力？

在“多对多”的供应链系统中，既涉及供应商/零售商之间的水平竞争，也涉及供应商和零售商之间的垂直竞争。供应商/零售商之间的水平竞争没有商品流动，是相互替代的关系。鉴于Chen 等[9]的研究显示，垂直供应链权力关系比水平供应链权力关系对单个企业或整个供应链的财务绩效影响更显著。为了简化模型而不影响研究目的，本文假设供应商/零售商之间的市场力量是相等的，因而采用Cournot博弈模型。尽管Cournot 博弈最早应用于寡头垄断的市场竞争，但后来的研究者们也将其应用到了多个具有同等市场权力的水平竞争者之间的博弈[10-11]。

供应商和零售商之间的垂直竞争存在商品流动，他们的竞争关系体现在对批发价格有相反的利益诉求。关于供应链垂直竞争，根据市场力量的变化，可采用Nash 博弈和Stackelberg 博弈来体现。Nash 博弈体现了博弈双方势均力敌，没有谁具有先动优势，博弈双方同时决策[12]。Stackelberg 博弈则体现出市场主导方的先动优势。近年来的供应链垂直竞争研究中，采用Stackelberg 博弈体现供应链上下游权力差异的文献很多[13-15]。从权力结构对利润的影响来看，较为一致的研究结论是，权力主导方具有优先决策权，因此具有先动优势，可以获得更高的利润水平。但也有研究者认为企业是否能受益于结构权力还受到诸如需求函数、需求不确定的影响方式[4-5]以及价格敏感系数[9]等因素影响。

基于上述研究，本文分别运用Cournot-Stackelberg博弈、Market-Stackelberg 博弈模型和Market-Nash博弈，来讨论“多对多”供应链中上游供应商主导权力逐渐降低、下游零售商权力逐渐增加的过程。1) Cournot-Stackelberg 博弈中，供应商具有供应链主导权力。供应商/零售商之间进行水平的Cournot博弈，供应商与零售商进行供应商主导的Stackelberg博弈。该博弈中，供应商的供应链主导权力最强。2) Market-Stackelberg 博弈中，供应商仍具有供应链主导权力，但是零售商将采购预算作为决策变量，以削弱供应商的主导权力优势。Korpeoglu 等[7]的研究将其命名为Market Game，本文为了同时展现供应链系统中的水平竞争和垂直竞争，将这种添加采购预算决策的博弈称为Market-Stackelberg 博弈。一些连锁超市与强势品牌供应商之间的竞争更类似于这种关系。3) Market-Nash 博弈中，供应链主导权力是均衡的，所有供应商和零售商同时作出决策，零售商仍然以预算作为决策变量。普通零售商和非品牌供应商之间的竞争多类似于这种博弈，另外势均力敌的品牌供应商和零售商也可能出现这种情况。

与本文最相近文献[4-5,9]，都是基于博弈论的框架，研究结构权力对供应链的影响。本文与这些文献的不同之处在于：1) 在研究目标上，主要研究市场竞争强度和市场波动对供应链主导权力优势的影响。2) 在建模上，构建一个需求不确定的“多对多”的供应链系统，通过供应商和零售商的数量变化来模拟市场的竞争强度；通过一个随机分布建模末端市场不确定，以剔除需求函数形式 (线性或非线性)对研究结果的影响；通过3 种博弈模型体现供应商主导权力逐渐被削弱的过程——绝对主导权力-主导权力削弱-结构权力相同。

1 问题描述

本文研究市场不确定背景下，多个供应商S通过批发市场向多个零售商R供货的情形如图1。假设每个零售商r面对各自的独立终端市场，每个终端市场Dr具有不确定性。Dr服从一个分布，其累积分布函数为F(x) ，概率密度函数为f(x) 。其中，概率密度函数f(x) 具有递增广义失败率 (increasing generalized failure rate， IGFR)，即需求函数Dr满足IGFR的特性。现实中，来自不同城市或地区的零售商在同一个批发市场/网络平台采购产品的模式符合该假设。根据假设，本文提到的水平竞争都指批发市场上的竞争，供应商是对需求的竞争，竞争压力体现在销售上；零售商是对货源的竞争，竞争压力体现在采购上。同时，假设供应商与零售商之间具有完全信息，均属风险中性者，追求各自利益最大化。零售商r∈{1,2,···,R} 以 批发价w从市场获取订购量qr，总订购量为再以零售价p销售产品。对供应商而言，每供应一单位产品的成本为c，用os表示供应商s∈{1,2,···,S} 向批发市场销售的数量，总生产量为其中，O-s表示除了供应商s之外的所有供应商的总生产量。总供给和总需求通过批发价格实现供需均衡，即Q=O。πs和πr分别表示供应商s和零售商r的利润，则有

分别运用Cournot-Stackelberg 博弈、Market-Stackelberg 博弈和Market-Nash 博弈3 种模型模拟上游供应商主导权力逐渐减低，下游零售商权力主权增加的博弈过程，其时序如图2 所示。

图2 博弈时序图Figure 2 Time sequences of games

2 模型建立

本文中，上标*表示最佳响应函数，上标C、M和N 分别表示Cournot-Stackelberg 博弈、Market-Stackelberg 博弈和Cournot-Nash 博弈模型，下标s、r分别代表供应商、零售商。本文用C-S 博弈、M-S 博弈和M-N 博弈分别代表Cournot-Stackelberg博弈、Market-Stackelberg 博弈模型和Market-Nash博弈。3 种博弈的特点如表1 所示。

表1 C-S 博弈、M-S 博弈与M-N 博弈对比Table 1 Comparison of C-S game, M-S game and M-N game

2.1 卖方具有主导权力的Cournot-Stackelberg 博弈模型

在供应商主导的Cournot-Stackelberg 博弈中，供应商之间和零售商之间均属于Cournot 竞争，但是供应商具有更强的市场力量具有先动优势，其与零售商之间采用Stackelberg 博弈。在决策的第1 阶段，每个供应商通过考虑产量对批发价格的影响确定一个产量水平 (产量越高，批发价格越低，在市场出清的博弈均衡中，均衡产量和均衡批发价格表现出一一对应的函数关系)；在第2 阶段，每个零售商根据终端市场的价格关系确定出采购量与批发价格的最优对应关系 (或者说对给定的某个批发价格，其对应的最优采购量)。双方的决策目标都是追求期望利润最大化，供应商和零售商的期望利润函数分别表示为

通过逆向归纳法求解，结果如表2 所示。

表2 博弈均衡策略和利润Table 2 Game equilibrium strategies and profit

证明零售商首先根据利益最大化原则决定订购量与批发价格的函数关系，由pF(qr)=0 ，得qr=F-1，则w=p(1-F(qr)) 。在市场出清的基础上，均衡总产量等于均衡总采购量，即O-s。然后，供应商根据零售商订购量与批发价格的对应函数关系，确定最优的生产量。将os=代入式 (3)，对批发价格求一阶导，可得c。证毕。

2.2 卖方主导权力削弱的Market-Stackelberg 博弈模型

与Cournot-Stackelberg 博弈相比，Market-Stackelberg 博弈最大不同点在于，作为跟随者的零售商将决策变量从采购量变成了采购预算。然后通过采购预算信息来影响供应商的决策。该模式下，决策的第1 阶段，每个供应商通过考虑其对批发价格的影响来决定其生产量；第2 阶段，每个零售商考虑其对批发价格的影响，确定其采购预算。批发价格由总采购预算和总产量共同决定，每个零售商的采购量则由其采购预算和均衡批发价格决定。设零售商r∈{1,2,...,R} 的采购预算为br，所有零售商的预算为B=其 中，B-r表 示 除 零 售 商r之外的所有零售商的总采购预算。

此时，供应商和零售商的最优化问题为

采用逆向归纳法求解，可得Market-Stackelberg博弈下各成员均衡决策，如表2 所示。

证明首先，由式 (5) 和式 (6) 对br求导得其 次，将w、qr的 表 达式代入零售商的期望利润函数，令可得。根据式 (5) 可将批发价格的表达式写成wM∗=然后，供应商考虑自身利益最大化，对生产量os进行一阶求导，令最后，将均衡解代入利润表达式，可得供应商s和零售商r的利润 (见表2)。证毕。

2.3 买卖双方权力均衡的Market-Nash 博弈模型

与前面两种博弈时序不同，在买方采用预算约束的情况下，考虑上下游同时进行决策的情况，建立上下游之间权力结构平衡的Market-Nash 博弈模型。在该模型中零售商和供应商分别同时决策采购预算和生产量。因此求解Market-Nash 模型，只需将之前Market-Stackelberg 模型中的目标函数 (7) 和(8) 分别关于采购预算br和生产量os求一阶导数并令其等于0，即联立求解得

2.4 博弈均衡解对比分析

综上，为进一步对比分析3 种博弈下供应链策略差异，将上述所得均衡解分别代入对应的利润表达式，可得供应商和零售商的最优收益，具体如表2 所示。

根据上述结果，可得到以下的命题。

命题1在“多对多”的供应链中 (S≥2,R≥2 )，零售商的订购量决策满足如下结果。

1) 3 种博弈策略下，零售商订购量均衡表达式分别为

2) M-S 博弈中零售商均衡订购量恒小于C-S 博弈，即。

3) 3 种博弈下，零售商订购量与供应商数量呈正相关，并且，除C-S 博弈外，订购量与零售商数量也呈正相关。

证明由于需求满足广义递增失败率 (IGFR)，即是一个递增函数，根据这个假设可以得到

根据博弈中订购量均衡表达式

作一个简单的代换可得

在C-S、M-S 博弈中，订购量均衡表达式为

由于 Ω (q•r) 是 关于q•r的增函数，那么对于给定的参数c、p， 显然S越大，则 对应的q•r越大，即q•r是关于S的增函数。而根据反函数和隐函数求导法则，M-N 博弈中，

因此，3 种博弈中零售商订购量与供应商数量呈正相关。同理，在M-S 和M-N 博弈中，利用反函数和隐函数求导法则可得到

即订购量与零售商数量也呈正相关。而在C-S 博弈中，均衡解能明显看出订购量与零售商数量没有关系。命题1 第3) 得证。

由于各零售商面临独立同分布的末端市场，那么零售商的订购量可以被看作流入末端市场的产品数量。由命题1 第2) 可得，供应链中供应商的结构权力影响着末端市场的产品流入量。当零售商以预算作为决策变量来约束供应商的主导权力时，会降低末端市场的产品流入量。命题1 第3) 显示，当供应商为绝对主导的时候，零售商数量的变化不会影响每个零售商的均衡采购量。而当供应商主导权力逐渐变弱的时候，零售商数量增加会刺激每个零售商提升均衡采购量。该结论给供应商提供了管理启示：当供应商主导权力削弱时，他们可以通过积极地开拓新市场来增加已有零售商的压力，刺激零售商提升采购量，从而缓冲权力削弱带来的不利影响。

命题2在“多对多”的供应链中 (S≥2,R≥2 )，供应商的生产量决策满足如下结果。

1) 在3 种博弈策略下，供应商的最优生产量分别为

3) 3 种博弈中，供应商生产量与零售商数量呈正相关，与供应商数量呈负相关。

证明同命题1 证明。

由命题2 可知，由于批发市场的供需均衡，总产量与总采购量是相等的，因此命题2 第2) 与命题1 第2) 是对应的。都说明了零售商采用预算决策削弱供应商主导权力会降低总均衡产量 (市场总产品流入量)。命题2 第3) 显示，无论供应商是否占据主导权力，只要预测到零售商数量增加，则一定会增加产量，预测到供应商增加则会减少产量。

命题3在“多对多”的供应链中 (S≥2,R≥2 )，批发价格决策满足如下结果。

1) 在3 种博弈策略下，最优批发价格分别为

2) M-S 博弈中市场批发价格恒小于C-S 博弈，即wM∗＜wC∗。

3) 与C-S 和M-N 博弈相比，M-S 博弈中的批发价格w由供应商的生产决策和零售商的订货决策共同决定。

证明略。

对比命题3 第1) 和命题1 第1) 可发现，CS 博弈中，无论是零售商均衡采购量还是市场均衡价格都不受到零售商数量影响。这是因为零售商的末端市场是独立的，供应商没有产能限制。因此尽管零售商数量增加，供应商总是能提供与之匹配的产量，从而无法影响到批发价格。命题3 第2) 显示，M-S 博弈中市场批发价格小于C-S 博弈，说明零售商以预算作为决策变量确实能为自己争取利益，获得更低的批发价格。M-S 博弈描述了市场中常见的一种场景：零售商带着一定的资金到批发市场购买产品，并根据有限的资金预算与供应商讨价还价，体现了零售商的买方权力。但并不是说零售商权力增加一定能影响到批发价格。在 M-N 博弈中，尽管零售商获得了跟供应商一样的市场权力，但是批发价格只与供应商数量和生产成本有关。命题3 揭示的管理启示如下：零售商适当的市场权力能够为其争取更低的采购价格；而当零售商拥有与供应商相当的权力后，运用其权力优势压低采购价格已经难以实现，此时降低采购价格的有效途径是寻求更多的供应源，鼓励更多供应商加入市场。

综合命题1 ~ 3，可发现在“多对多”的供应链系统下，均衡决策与结构权力之间的关系不同于“1 对1”供应链。Shi 等[4]在研究“1 对1”供应链权力结构对供应链影响时，得出的结论是，批发价格(采购量) 随供应商权力增加而增加 (减少)，随零售商权力增加而降低 (增加)。在“多对多”的系统中，随着供应商权力降低，买方权力增加，批发价格和采购量并没有这种绝对单调的表现。在“多对多”的系统中，权力结构对均衡决策的影响强度很大程度上受到市场波动和竞争强度的干扰。

基于上述均衡解分析，鉴于模型的复杂性，接下来将采用数值实验的方法，分析3 种博弈状态在面对需求波动、竞争强度等外部因素变化时的决策变化和供应链绩效。数值实验旨在分析 (图示化) 需求波动和竞争强度的影响趋势，因此在进行数值实验时，参数取值并不指向具体案例。由于正态分布是一类具有代表性的随机分布，因此数值实验采用正态分布表示市场需求的随机性。

3 需求波动对结构权力优势的影响

结合表2 的均衡解，参数设置如下：Dr∼N(30,202)，R=5 ，S=10，p=3 ，c=1 。采用Matlab工具计算各决策变量和利润的显性解，比较不同博弈类型下的策略差异。

3.1 均衡产量与批发价格

市场需求波动影响企业的经营决策，因为高需求不确定性意味着高错配成本。尽管集中式供应链总受益于需求不确定性的减少，但当考虑到不同供应链成员之间的战略互动时，需求不确定性的减少如何影响供应链成员的绩效还不太清楚。因此，本小节将研究上下游不同权力形势下，需求波动 σ 如何影响供应链成员的决策问题。通过将 σ 从5 递增至50 来生成更多的问题实例，实现敏感性分析，并得到以下结论。

1) 分析均衡产量 (均衡采购量有相同的趋势，故略)。如图3 (a) 所示，随着需求波动的增加，卖方权力最大的C-S 博弈中均衡产量的变化最大，权力均等的M-N 博弈变化最小。可见在卖方主导的时候，市场波动对供应链均衡产量会带来很大影响，卖方的优先决策权促使牛鞭效应的放大作用影响了整个供应链。而随着卖方主导权力的稀释，市场波动对均衡产量的影响变得平缓许多。

图3 均衡决策对需求波动的反应Figure 3 Responses of equilibrium decisions to demand fluctuations

2) 分析批发价格的变化。如图3 (b) 所示，随着市场波动的增加，C-S 和M-S 下均衡批发价格均急速下降，并且C-S 模式下的变化幅度最大，MN 模式基本没有变化。

总体来讲，首先，面对市场波动的变化，卖方权力最大的C-S 模型中的均衡产量和均衡价格都会产生较大幅度的变化，M-S 相对变化幅度小一点，而比较稳定的是权力均衡的M-N 模式。其次，从批发价格优势上来看，供应商的主导权力优势在市场波动较小时比较明显；在市场波动较大时反而被动，容易造成供给过多，价格骤降，增产不增收的局面。

3.2 供应链参与者利润

关于某种博弈类型下，需求波动对供应链成员利润的影响趋势已经有不少文献进行了分析。一般认为供应商会受益于需求波动的减少，而零售商则不一定[4]。因此本节仅关注需求波动对供应链权力优势的影响，即考察由于结构权力带来的利润优势如何受到需求波动的干扰。

1) 观察供应商利润，如图4 (a) 所示。当需求波动较小时，C-S 博弈使得供应商利润最大，MN 的供应商利润最小，即供应商利润随着其权力的削弱而降低了。当需求波动继续增加时，M-N 的供应商利润逐渐接近C-S 和M-S，后期超过M-S。可见需求波动很大时，供应链主导权力无法给供应商带来更高的利润，此时供应商获取市场权力意义不大。

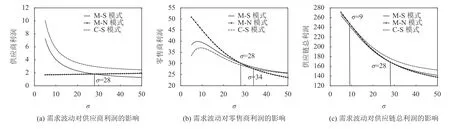
图4 均衡利润对需求波动的反应Figure 4 Responses of equilibrium profit to demand fluctuations

2) 分析零售商的利润，如图4 (b) 所示。需求波动较小时，零售商权力最大的M-N 博弈使得零售商的利润最大，C-S 博弈的零售商利润最低。即零售商的利润随着市场权力的增强而增加。当需求波动较大时，利润关系正好相反。可见当需求波动较大时，零售商也无心争取市场权力。

3) 观察供应链总利润，该变化趋势与零售商类似，但是总体来讲变化不大。

当市场需求波动较小的时候，参与者的利润随着其供应链主导权力的增加而增加，此时供应商会为了维护自己的供应链主导权力花费更多成本，零售商也会为了争取买方权力而增加投入。但当需求波动很大时，3 种博弈下的利润差距明显减小，即供应链主导权力带来的利润优势不再显著，此时，若获取主导权需要高额成本，那么供应链成员都没有动机去争取市场主导权。

4 竞争强度对权力结构优势的影响

随着电子商务的大规模发展，供应链中融入了更多的供应商或零售商，那么，面对供应链成员数量的增加，供应链结构权力优势会产生怎样的变化？本节通过改变市场参数 (包括零售商数量R和供应商数量S) 来模拟市场竞争强度，观察供应链决策以及利润的变化特征。

4.1 供应链的均衡策略

通过编程求解总结了3 种博弈下供应链参与者数量对供应链均衡策略和的影响，如表3 所示。1) 首先分析每个供应商的均衡产量。3 种博弈下，产量决策随供应链成员数量的变化趋势是一致的，都是随着供应商数量增加而减少，随着零售商数量增加而增加。2) 其次分析均衡订购量，只有在供应商绝对主导的时候，均衡订购量不受零售商数量影响；其他情况下，竞争强度的增加都会提升均衡订购量，提升末端市场的产品流入量。3) 分析均衡批发价格。在面对供应商数量增加时，3 种博弈模式下的批发价格都表现为下降，可见批发价格随着供应商数量增加的递减趋势不受权力结构的影响。然而，在面对零售商数量变化时，不同权力结构的批发价格却呈现不同变化趋势。在C-S 和M-N 博弈中，零售商数量变化不影响批发价格，而在M-S 中零售商数量增加会促使批发价格上涨。

表3 供应链成员数量变化时的均衡策略1)Table 3 The equilibrium strategy with variable number of supply chain members

4.2 供应商的利润

上游的竞争强度和下游的竞争强度，对供应商的利润及其对主导权力的态度会产生不同的影响，如图5 所示。

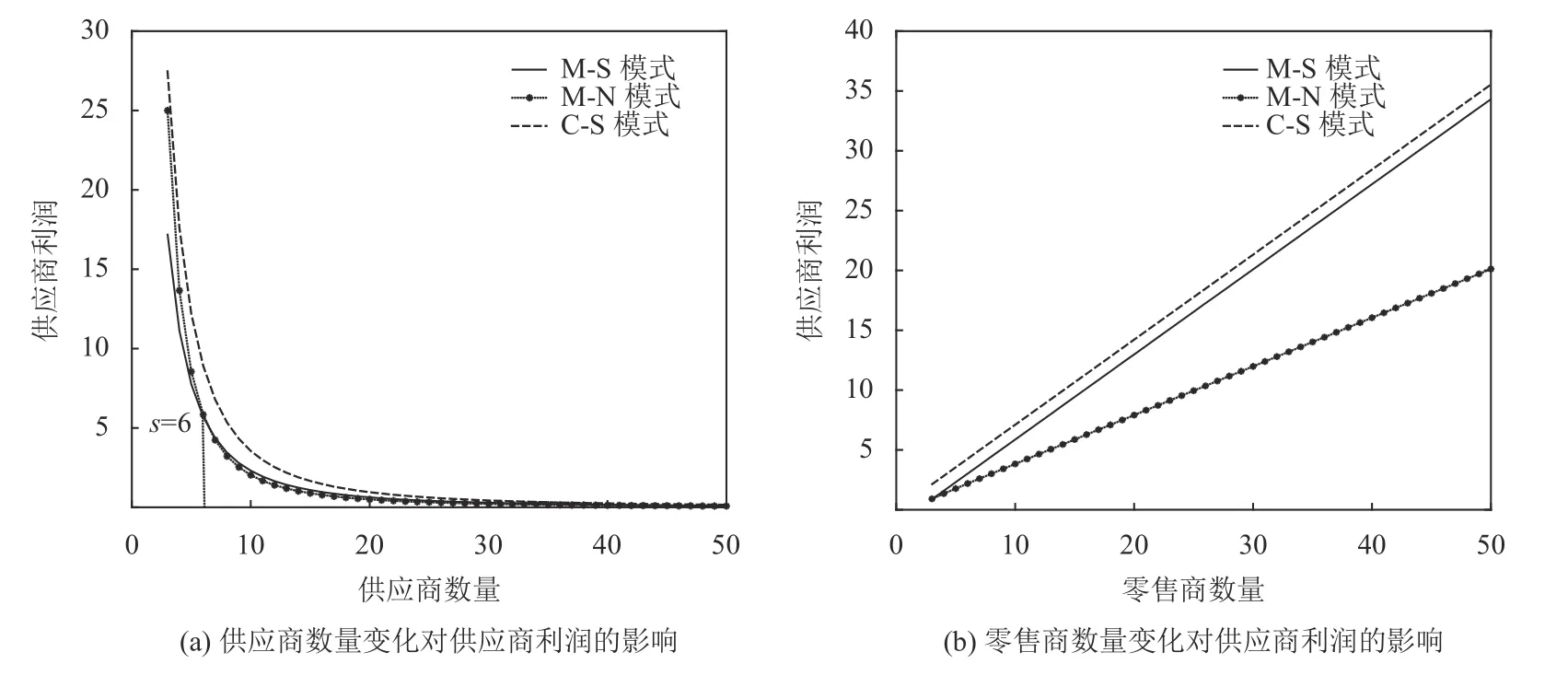
图5 供应商的均衡利润对竞争强度的反应Figure 5 Responses of suppliers' equilibrium profit to competition intensity

1) 面对供应商数量的增加，如图5 (a) 所示，上游的竞争强度增加，3 种博弈下供应商的利润都呈明显下降趋势。当供应商数量较少时，供应商市场权力较大的C-S 博弈模型中，供应商利润最高，M-S和M-N 模型中的供应商利润很接近。当供应商数量较多时，3 种博弈模型的利润基本一致。可见在竞争强度较大时，供应链参与者没有动力争取市场权力。

2) 面对零售商数量的增加，如图5 (b) 所示，3 种博弈下供应商的利润都呈明显上升趋势。并且当零售商数量较多时，市场权力越大的博弈促使供应商获得越多的利润。因此当下游竞争激烈时，供应商会努力争取供应链主导权力。这个结果是比较直观的。因为在模型中，下游零售商面临独立的需求市场，因此零售商数量增加相当于开拓了新市场，总需求增加，促使零售商在采购市场的竞争更加激烈。此时上游供应商的主导权力带来更大的优势。换个角度来看，对于拥有供应链主导权力的供应商，不断拓展新的市场能为其带来更大的利润优势。现实中，汽车、电脑、手机等相对高价值的消费品，其生产商一般具有纵向主导权，而这些企业往往乐于开拓新市场，这些产品也更可能销往世界各地。

综上所述，上游激烈的横向竞争会促使上游放弃争夺供应链主导权力，而下游激烈的横向竞争则会促使上游积极争夺供应链主导权力。

4.3 零售商的利润

上游的竞争强度和下游的竞争强度，对零售商的利润及其对供应链主导权力的态度也会产生不同的影响，如图6 所示。

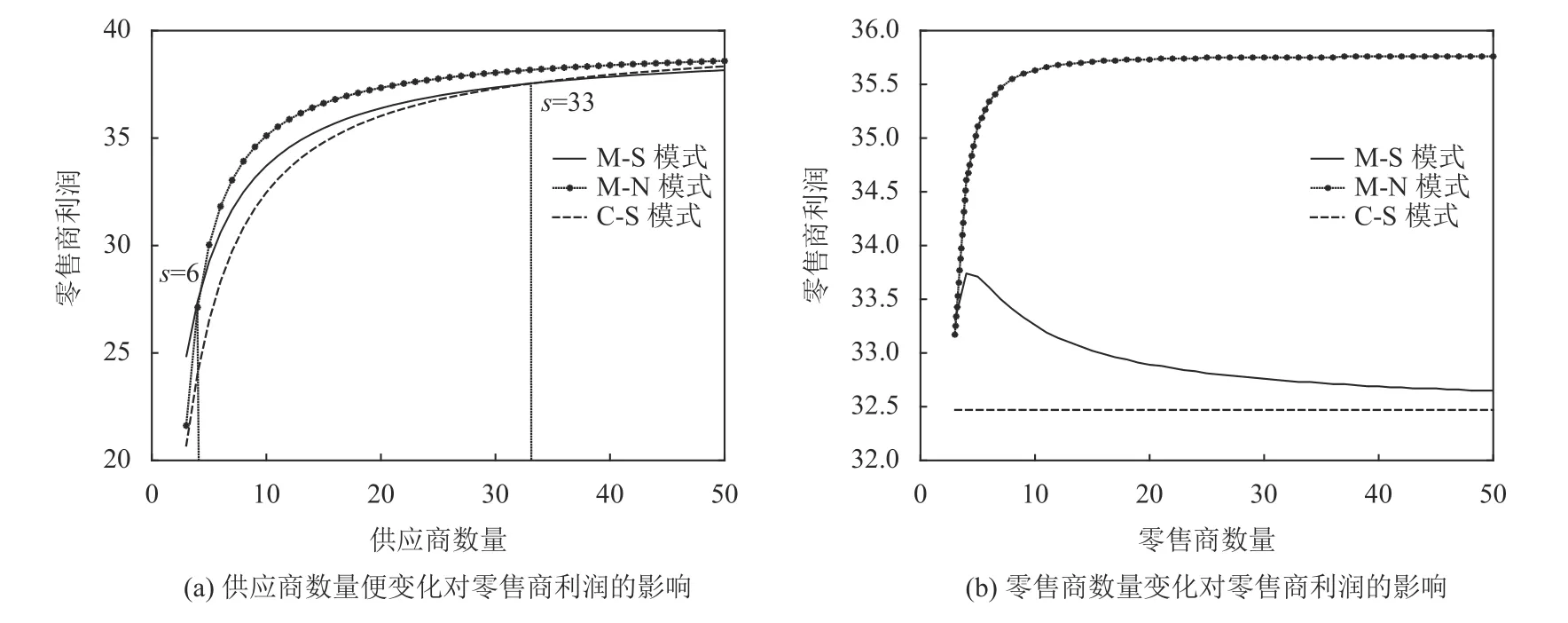
图6 零售商的均衡利润对竞争强度的反应Figure 6 Responses of retailers' equilibrium profit to competition intensity

1) 面对供应商数量的增加，如图6 (a) 所示，上游的竞争强度增加，3 种博弈下零售商的利润都呈明显上升趋势。当供应商数量较少时，零售商市场权力较大的M-N 博弈模型中，零售商利润最高，其次是M-S 模型，最低的是C-S 模型。当供应商数量较多时，3 种博弈模型的利润基本一致。可见在上游竞争强度较大时，零售商没有动力争取市场权力。

2) 面对零售商数量的增加，如图6 (b) 所示，零售商市场权力最大的M-N 博弈下,零售商利润具有明显的上升趋势，M-S 博弈下的零售商利润先上升再下降。但是M-N 和M-S 都高于市场权力最小的C-S。即当零售商横向竞争激烈时，争取买方权力能够提升利润水平。这是因为，上游竞争激烈时，卖方具有更大的销售压力，其供应链主导权力在这种销售压力面前无法体现优势，因而零售商无需争夺市场权力；而在下游竞争激烈的时候，买方具有更大的采购压力，如果此时上游还具有供应链主导权力，那么零售商利润受到很大损害，因此争取市场权力能够让零售商平衡这种采购压力。

综合来看，供应商数量变化时，3 种博弈下零售商利润区分不大，因此供应商数量变化对零售商改变市场权力的诱导作用不大。而零售商数量变化却相反。当零售商竞争激烈的时候，具有均衡权力的M-N 博弈促使零售商获得最高利润，且远高于另外两种博弈结果。此时买方权力的争取，会使得零售商利润大大增加，因此，零售商愿意花费较高的代价争取市场权力。

4.4 供应链总利润

将供应链上的S个供应商和R个零售商的利润总和作为该条供应链的总利润，则3 种博弈下的总利润均可以表示为考察供应链总利润关于水平竞争强度的变化，可得到命题4。

命题43 种博弈结构下，供应链总利润均随着供应商和零售商数量的增加而增大，即

证明结合表2，C-S 博弈均衡下，供应链的总利润为

上式对供应商数量S求一阶导有

同理，M-S 和M-N 博弈均衡下,

可见市场竞争的加剧有可能会损害单个个体的利益，但是就社会整体来看，竞争促使了总福利增加。因此鼓励竞争有助于社会整体经济的发展。

5 结论

为研究“多对多”供应链中市场主导权力优势的问题，本文以多个供应商和多个零售商组成的供应链为研究对象，采用C-S 博弈、M-S 博弈模型和M-N 博弈3 种博弈类型，模拟了上游供应商市场权力逐渐降低，下游零售商市场权力逐渐增强的市场竞争情况。对比分析了不同的市场主导权力下的供应链均衡策略和供应链绩效，以及它们面对市场波动和竞争强度变化时的反应。结果表明如下。

1) 结构权力对市场均衡批发价格产生影响。首先，相比供应商市场权力最大的C-S 博弈，采用预算约束行使买方权力的M-S 博弈使得市场均衡批发价格更低。其次，在强烈的需求波动下，相比CS 博弈和M-S 博弈，上下游权力均衡的M-N 博弈能够稳定均衡批发价格。

2) 需求波动会影响主导权力的利润优势。当市场需求波动较小的时候，供应链参与者的利润随着其供应链主导权力的增加而增加，此时供应商会为了维护自己的供应链主导权力花费更多成本，零售商也会为了争取买方权力而增加投入。但当需求波动很大时，供应链主导权力带来的利润优势不再显著，此时，若获取主导权需要高额成本，那么供应链成员都没有动机去争取市场主导权。

3) 竞争强度会影响主导权力的利润优势。上游供应商的激烈竞争会促使上游放弃争夺供应链主导权力，且对零售商争取市场权力的诱导作用不大，可能因此形成上下游权力均衡的M-N 博弈形式；而下游激烈的横向竞争则会同时刺激供应商和零售商积极争夺供应链主导权力。

4) 市场竞争的加剧有利于提升供应链总利润，因此鼓励竞争有助于社会整体经济的发展。

本研究将对市场权力的研究拓展到了“多对多”的供应链，研究对象适合市场发展实际。在对主导权力结构的模拟上，抓住了主导权力逐渐变化的过程。本文研究结论与“1 对1”供应链的结论有差异。在“多对多”的供应链中，主导权力的利润优势与需求波动及竞争强度息息相关。因此对企业来讲，争夺市场权力并非总是占优策略。本研究还存在一些局限性，未来可在以下两个方面进一步拓展：(1) 本文主要讨论的是纵向竞争中供应链主导权力的变化，横向竞争中各成员权力均等，在未来的研究中可以进一步讨论横向竞争中也存在权力差异的情况；(2) 本文假设了零售商面临独立的终端市场，即零售商只在采购市场存在竞争，未来可拓宽到零售商在销售市场也存在竞争的情况。