单机差异尺寸作业外包-生产-配送联合调度

耿建一，刘 乐

(济南大学 商学院，山东 济南 250002)

随着按单生产 (make to order, MTO) 模式的普及，许多制造企业的库存维持在接近于零的水平，使生产与配送两个供应链环节之间衔接愈加紧密。在零成品库存这一新常态下，生产与配送的协同决策是供应链视角下制造企业实现降本增效的重要出路[1]。因此，生产-配送联合调度问题 (integrated production and distribution scheduling problem, IPDSP) 成为近年来供应链管理领域的研究热点。

IPDSP 研究已涉及多种机器环境类型，如单机[2-3]、平行机[4]、流水车间[5-6]等，它们都基于传统生产模式，即一台机器上同一时刻仅加工一个作业或一道工序。在集成电路烧机测试、陶瓷烧制等场合下作业的加工并不基于该模式，而是采用并行批加工模式 (parallel batching, p-batch)。p-batch 模式契合许多制造商提高产品吞吐量、充分利用产能的发展诉求。在p-batch 模式下分配到同一生产批次中的作业在同一台批处理机上一起加工，一个批次的工时由其中用时最长作业的工时决定[7]。同一批次的作业具有相同的开工与完工时间，但其尺寸各异，尺寸之和不超过批处理机容量。p-batch 模式下的IPDSP研究近年来发展迅速，涌现出一批优秀成果，如文献[8-12]。

IPDSP 研究中配送模式按运载能力和发货运输方式的不同区分。可派遣车辆的数量及其载荷量是衡量运载能力的两大指标。在常见的发货运输方式中，分批配送 (batch delivery, BD) 方式追求车辆满载运输以减少派运车次，是成品货运中最有效降低成本的策略之一[3]。根据同一批次送达客户数的不同，BD 方式有直接发货、环程发货之分[1,4]。在直接发货型BD 方式下每辆车装载的产品都运往同一客户。文献[2,4-5,8-9,11]都是在直接发货型BD 方式下开展的IPDSP 研究工作。这一BD 方式常见于渠道商 (如零售商、经销商) 作为单一客户的生产-配送管理系统中。渠道商在制成品流通中发挥集散作用，不仅成品需求量大，而且对它的配送服务具有点到点、多车次的特点。

由于大多数IPDSP 是NP 难的[1]，IPDSP 研究中运用的优化技术主要有精确解法[2]、确定型启发式算法[9,11]和元启发式算法[3-6,8,10,12]三类。由于具有良好搜索效率，元启发式算法是IPDSP 研究中运用最多的求解技术。作为元启发式算法之一，遗传算法 (genetic algorithm, GA) 备受IPDSP 研究者青睐。在Noroozi 等[3]、Joo 等[4]、Qin 等[5]的研究中均成功运用GA 对IPDSP 模型进行高效求解。

外包 (outsourcing) 是当代制造企业快速响应市场波动、规避产能短缺风险、提升交付能力的重要策略之一[13]。在p-batch 模式下工时明显更长的作业会对同批次其他作业的完工时间造成延迟影响；若此时合理运用外包策略把它们外包出去，则有助于提升产品交付水平和内部产能利用率。p-batch 模式下可外包作业批调度优化已有研究成果问世[14]，但总体来看还处于起步阶段。p-batch 模式下作业外包-生产-配送联合调度较之更复杂，在研究进展上更滞后于现实管理需求。作业的外包决策给p-batch模式下管理者的作业生产与配送联合调度工作带来挑战，使决策的内容涉及作业外包选择、内部作业批调度、成品配送调度3 个环节。它们在实际运营中往往分部门、分阶段独立执行，导致了运营成本居高不下、周期冗长等痛点问题。为此，本研究聚焦p-batch 模式下基于单机环境和直接发货型BD 方式的作业外包-生产-配送联合调度问题 (integrated job outsourcing-production-distribution scheduling problem, IOPDSP)，旨在一体化高效得出作业外包选择方案、内部批调度方案和成品分批配送方案，以期为p-batch 模式下制造企业的作业外包、生产与配送联合调度管理提供参考建议。

1 问题描述与建模

1.1 符号定义

IOPDSP 的主要参数符号及其说明见表1。其中，j、k、l分别是对作业、内部加工批次和配送批次的索引编号；在联合调度解π=[Oπ,B,D]中 ，B={Bk;k=1,2,···,b} 由b个 内部加工批次组成，D={Dl;l=1,2,···,d} 由d个配送批次组成。TCπ=OCπ+IPCB+DCD；不发生歧义时TCπ、OCπ、I PCB、D CD分别简写 为TC 、O C、IPC、DC 。另 有

表1 IOPDSP 中的参数符号及其说明Table 1 Notations and their definitions in IOPDSP

1.2 假设条件与问题描述

IOPDSP 假设条件如下 。

1) 批处理机采用p-batch 模式，在同一时刻最多处理一个加工批次，不允许批次之间抢占机器；

2) 所有作业都来自同一客户的订货；

3) 每个作业的尺寸小于批处理机容量，经加工后其尺寸不发生改变；

4) 外包作业的加工与配送环节包干委托给单一转包商完成；

5) 制造商内部批加工总成本与内部批加工总时长成正比关系，有 I PCB=λCmax(B) ；

6) 内部加工批次是分批配送的基本单位；

7) 配送车辆充足且最大载荷量统一，每完成一次送达任务都消耗相同的配送成本和时间；

8) 由于客户以制成品最晚送达时间衡量制造商的交付质量，提前完工的内部作业无需立即分批配送给客户，待全部内部作业都完工后再统一安排制成品配送方案；

9) 内部作业批加工与制成品配送两环节之间所耗库存成本折算到内部作业的批加工成本中。

IOPDSP 可描述如下。在t=0 时刻作业集J到达制造商，待其联合调度。这n个作业既可在内部完成加工并在制成后分批送达客户C1，也可外包出去，由转包商S1包干完成加工和配送任务。对确准外包的作业Jj，制造商为其支付外包成本oj。内部作业在单台批处理机上制成后，按BD 方式由同质车辆从制造商处送至客户C1处。在作业外包总成本受预算限制、机器容量和车辆载荷强约束条件下，IOPDSP 的目标是将各个作业分配到外包作业集或不同的内部加工批次，再将各内部加工批次分配到不同的配送批次(求得π∗=[O∗π,B∗,D∗])，使TCπ∗=OCπ∗+IPCB∗+DCD∗达到最小。

1.3 数学模型与理论分析

为建立IOPDSP 的整数规划模型，首先引入6 组0-1 决策变量xjk、yk、zj、ujl、vl和wkl(j=1,2,···,n;k=1,2,···,n;l=1,2,···,n)。

IOPDSP 的0-1 规划模型如式 (1) ~ (16)所示。

式 (1) 为模型的目标函数，即最小化作业运营总成本；约束 (2) 避免某个作业既被外包出去，又在内部加工的可能性，限定每个内部作业只在一个加工批次中；约束 (3) 排除某个作业既参与外包生产，又由制造商将其制成品送达客户的可能性，并限定每个制成品只在一个配送批次中；约束 (4) 保证每个内部作业都有相应的配送批次将其制成品送达客户；约束 (5) 排除某个内部作业所在的加工批次未被创建的可能性；约束 (6) 排除一个配送批次所含加工批次未被创建的可能性；约束 (7) 确保某个制成品所在的配送批次已被创建；约束 (8) 确保某个内部加工批次的制成品所在的配送批次已被创建；约束 (9) 和 (10) 联合保证若作业Jj在批次Bk中完成加工，其制成品是否安排在配送批次Dl中取决于配送批次Dl中是否包含批次Bk的制成品；约束(11) 保证若无任何作业被分配到一个内部加工批次中，则该加工批次不被创建；约束 (12) 保证若无任何内部加工批次的制成品被分配到一个配送批次中，则该配送批次不被创建；约束 (13) 确保每个内部加工批次中作业尺寸之和不超过批处理机容量；约束 (14) 保证每个配送批次中制成品尺寸之和不超过车辆最大载荷量；约束 (15) 施加作业外包总成本不超过给定预算值的硬约束；约束 (16) 指明6 组决策变量的二元属性。

考虑基于下列假设的IOPDSP 特例：所有作业具有相等且足够高的外包成本值，有o1=o2=···=on＞G(故无作业参与外包生产)；车辆的单车次配送 成 本 µ =0 (故 D C=0 )；所 有 作 业 的 内 部 工 时 相等，即p1=p2=···=pn。在 上 述 假 设 下IOPDSP的目标函数等价于最小化加工批次数。若把加工批次视作箱子，此时IOPDSP 退化为一维装箱 (bin packing) 问题：待装箱的物品数为n；箱子容量为Q1； 物品体积为sj，目标函数为最小化箱子 (加工批次) 数。一维装箱问题已被证明是NP 难的问题[15]。作为一维装箱问题的泛化，IOPDSP 的计算复杂性不低于一维装箱问题，故IOPDSP 也是NP 难问题。

作业外包决策环节是解决IOPDSP 的首要任务，可根据以下性质直接判断符合特定条件的作业应加入或不应加入外包作业集。

性质1若作业Jj满足oj＞λpj+µ ，则它在π∗中不加入。

性质2若作业Jj满足pj=pmax(J) ；oj＜λ[pmax(J)-pmax(J|{Jj})]，则它在π∗中应加入。

若将满足性质1 中指定条件的作业加入外包作业集，则通过估算、比较由此直接产生的 T C 增加量和减少量，可推断存在比更优的联合调度解。π∗定义上的前后矛盾可反证出性质1 成立。性质2 亦可通过该思路证实。

2 遗传算法设计

为求解IOPDSP，本节设计出改进型遗传算法(improved genetic algorithm, IGA)。IGA 的改进之处体现在两方面。一是在染色体编码上，考虑到IOPDSP 中的3 个决策环节和π的三元组结构，对每个作业连续分配3 个基因位，分别对应作业外包状态、所在加工批次及其制成品的配送批次。二是将带精英保留的锦标赛选择、均匀交叉、均匀变异3 个进化机制组合应用于IOPDSP 的GA 求解中。上述三机制的单独应用效果已获认可，但它们的组合应用效果有待在IOPDSP 的求解中考察验证。

2.1 联合调度解的表示结构设计

IGA 中采用含 3n个元素的一维数组结构表示联合调度解π。该结构也是IGA 的染色体编码结构，每个元素对应一个基因位。在该结构中依照索引编号从小到大的次序为各个作业分别分配连续的3 个基因位，即g1、g2和g3。g1∈{0,1} ，指明当前作业的外包状态。g1=0 表示当前作业在内部完成加工；g1=1表示当前作业被外包出去。g2指明当前作业所在内部加工批次的索引编号，g2∈{0,1,···,n}。g2=0 表示当前作业不在任何内部加工批次中。g3表示当前作业制成品所在的配送批次。由于存在每个加工批次都仅容纳单个作业的可能，故g3∈{0,1,2,···,「n·Q1/Q2⏋} ，「r⏋表 示不小于实数r的最小整数；g3=0 表示当前作业不在任何配送批次中。由于每个作业仅有内部加工和外包加工两种选择，故每个作业在g1和g2上不能同时取0。另因外包作业采取包干的方式，当且仅当g1=1 时 作业在g2和g3上的值都为0。为保证出自同一生产批次的制成品在同一配送批次中送达，规定：若两个作业在g2上取值相等，则它们在g3上取值也相等。

考虑一个含6 个作业的IOPDSP 示例，取G=9 ，Q1=10，Q2=30 ， λ =1 ， µ =30 ，作 业 尺 寸、内 部工时和外包成本信息如表2 所示。图1 为该示例的一个可行解的表示结构图。其中，作业J1、J5被外包 出 去；内 部 加 工 分B1和B2两 批 次；作 业J2、J3和J6组 成B1， 作 业J4独 自 在B2中 ；加 工 批 次B1和B2的制成品组成唯一的配送批次D1。

图1 示例中一个可行解的表示结构Figure 1 The representation structure of a feasible solution in the example

表2 IOPDSP 示例中的作业信息Table 2 Information for jobs in IOPDSP examples

2.2 初始种群的生成

IGA 中采用随机方式生成初始种群 P op(0) 。该种群有 p opSize 条 染色体，每条染色体含 3n个基因位。P op(0) 中每条染色体按作业索引编号由小到大的次序逐步生成。对于满足性质1 中指定条件的作业，安排其到某个内部加工批次中 (g1上的值为0)；对于满足性质2 中指定条件的作业，安排其到外包作业集中 (g1上的值为1)；对于性质1 和2 中指定条件均不满足的作业，其在3 个基因位上的值从各自有效范围内随机产生。

2.3 染色体的适应度评价

染色体的合法性判定是其适应度评价的首要工作。IGA 中基于IOPDSP 特征的染色体合法性判定条件如下。

1) 作业外包总成本不超过G；

2) 每个加工批次所含作业尺寸之和不超过Q1；

3) 每个配送批次所含作业尺寸之和不超过Q2；

4) 每个作业在g1和g2上的值有且仅有一个为0；

5) 若两个作业在g2上取值相同，则它们在g3上取值也相同。

一条染色体及其对应的联合调度解π若违反上述条件之一，则被视为非法染色体，记其适应度值为0；若上述条件均满足，则被视为合法染色体。对认定合法的染色体，先按式 (1) 计算所对应π的目标函数值Z(π) ，再按式 (17) 计算适应度值。

其中，M代表Z(π) 的最大可能值，文中取

2.4 染色体选择机制

为避免高质量染色体从种群中快速消失，以及寻优过程易于陷入局部极优的问题，IGA 采用带精英保留的锦标赛选择机制产生新一代种群。IGA 中逐代执行的染色体选择步骤如下。

1) 从种群 P op(t) 中 选出适应度值最大的elitCount条染色体直接进入下一代种群 P op(t+1) ；

2) 从 种 群 P op(t) 中 随 机 选 取 t ournmSize 条 染 色体，将它们置入锦标赛选择池 t ournament 中；

3) 对选择池 t ournament 中所有染色体按适应度值排序，从中选出适应度值最大的染色体后置入下一代种群 P op(t+1) 中；

4) 重复执行步骤2) 和3) p opSize-elitCount 次，直到 P op(t+1) 中 染色体条数达到 p opSize 。

2.5 染色体交叉与变异

鉴于在染色体编码结构中为每个作业分配3 个基因位，为防止因交叉操作产生大量非法染色体，每个作业对应的3 个基因位需作为一个整体参与染色体交叉过程。IGA 借鉴文献[16]中的均匀交叉法来实施染色体交叉，具体步骤如下。

首先从种群 P op(t) 中随机选择2 条亲代染色体，分别为Parent1 和Parent2。然后判定染色体交叉执行条件pc＞random(0,1) 是否满足，pc为交叉率，反映均匀交叉的执行概率； r andom(0,1) 表示区间 (0, 1) 上产生的随机实数。若交叉执行条件满足，则按初始种群中染色体生成方式创建一个子代染色体Offspring。Offspring 中每个作业对应的3 个基因位都有50%的概率取值为Parent1 中相应基因位上的值，另有50%的概率取值为Parent2 中相应基因位上的值。最后让Offspring 取代Parent1，成为 P op(t) 中的一条染色体。图2 为面向示例的染色体均匀交叉过程示意图。

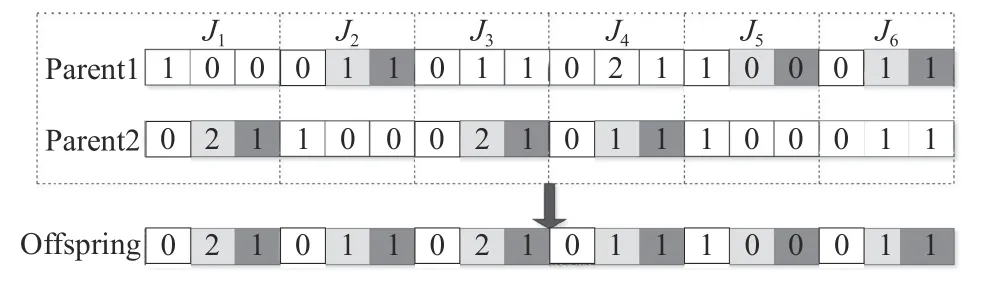
图2 均匀交叉过程Figure 2 Processes of uniform crossover

为保持新一代种群中染色体的多样性并避免轻易产生非法染色体，通过借鉴文献[17]中相关做法，IGA 中采用均匀变异的方式实施染色体变异，具体步骤如下。

首先从种群 P op(t) 中按指定顺序选出一条染色体，记作Chrm1，并按初始种群中生成染色体的方式生成另一条染色体，记作Chrm2。然后创建一个含 3n个元素的一维数组，用以保存变异后所得染色体Chrm3。

对染色体Chrm3 中每个作业，判定染色体变异执行条件pm＞random(0,1) 是否满足，pm为变异率，反映当前作业发生变异的概率。若上述条件满足，则Chrm3 中当前作业对应的3 个基因位取值为Chrm2 中相应基因位上的值。若不满足，则Chrm3中当前作业对应的3 个基因位取值为Chrm1 中相应基因位上的值。变异后所得Chrm3 取代Chrm1，成为种群 P op(t) 中的一条染色体。图3 为面向示例的染色体均匀变异过程示意图。

图3 均匀变异过程Figure 3 Processes of uniform mutation

2.6 迭代终止条件

IGA 中设定迄今最佳染色体的适应度持续无改进的最大迭代次数Imax=200n。IGA 会逐代更新并记录迄今最佳染色体，当它的适应度值经过连续200n次迭代未被更新时，IGA 终止运行。

2.7 算法步骤

IGA 的执行步骤如下。

步骤1设置下列参数的取值： p opSize ,elitCount,tournmSize,pc,pm,Imax。

步骤2按2.2 节所述生成初始种群 P op(0) ，设置迭代计数变量t，取其初值为1。

步骤3对种群 P op(t-1) 实施带精英保留的锦标赛选择机制，其过程按2.4 节所述执行。

步骤4对种群 P op(t-1) 先后实施均匀交叉和均匀变异操作，其过程按2.5 节所述执行，得到新一代种群 P op(t) 。

步骤5设置t←t+1，判断迭代终止条件是否满足。若不满足，则返回步骤3。

步骤6输出种群中最佳染色体所对应联合调度解及其目标函数值。

3 实例分析

3.1 实例描述

实例出自某陶瓷企业负责坯体烧制、外包及其制成品配送的管理一线。该企业中烧制坯体的设备是一台高温电窑炉，采用p-batch 模式，容量Q1=20 m3， 额定功率 P W=5 kW 。当地平均工业用电目录电价 E C=0.6 元/(kW·h) 。该企业单位时间上的批加工成本主要是单位时间上的用电成本，故λ=PW·EC·δ ， δ ＞0 为分时段的单位用电价格系数。该企业从第三方物流 (third-party logistics, 3PL) 公司租用车辆配送陶瓷制品，可租用的车型有多种。所有配送车辆都将陶瓷制品运往同一经销商处。该企业可将坯体烧制与制成品配送包干转包给合约制造商S1。考虑到该企业与经销商之间距离、路况和行驶油耗等因素，3PL 公司对所有车型给出每单位体积运力单车次的往返运输报价为 α ≈1.0 元/(m3·车次) 。对最大载荷量为Q2的车辆，其单车次配送成本µ=αQ2≈Q2元/车次。所关注的联合调度情景如下。该企业的管理一线接到22 个坯体的烧制与配送任务，这些坯体来自同一经销商的订货，各自尺寸、内部烧制时间和外包成本如表3所示，亟待利用合约制造商S1的产能，通过牺牲一定数额的外包成本而使 T C 显著下降。该企业中坯体烧制时间的决定因素有多种，如材质、厚度、釉面纹路等，与尺寸的相关度并不高。该企业肯付出的外包总成本有限，需事先根据经营情况和融资能力设定预算值G=为外包总成本容许率。

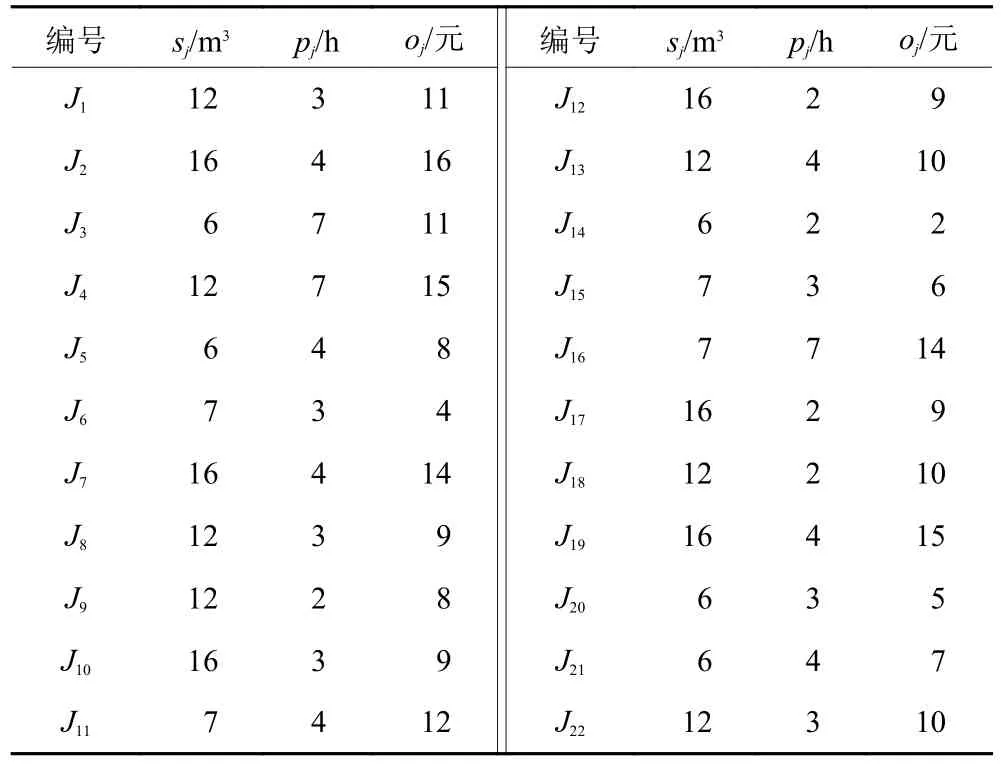
表3 实例中坯体的尺寸、内部烧制时间和外包成本信息Table 3 Sizes, inhouse firing time and outsourcing cost of ceramic bodies in the instance

3.2 基于实例的IGA 性能实验分析

本节对IGA 开展IOPDSP 上的性能实验分析，并与CPLEX 12.8 软件的求解结果进行比较。本实验所用程序以Java 语言编程实现，运行环境为处理器AMD Ryzen7 4800H；主频2.90 GHz；RAM 内存16.0 GB。预实验中对IGA 的重要参数进行校准，得出的取值建议为 p opSize=50，pc=0.95，pm=0.01, e litCount=5 , t ournmSize=5 。

本实验用到的6 个测试算例源于3.1 节所述实例。算例1 中坯体数为17，这17 个坯体的信息如表3中J1~J17对应信息所示；算例2 中坯体数为18，这18 个坯体的信息如表3 中J1~J18对应信息所示，以此类推。这6 个算例的其他参数取值如下：Q1=20 m3，Q2=40 m3， P W=5 kW ， δ =1.5 ， E C=0.6 元/(kW·h) ，µ=40 元/车次 ， η =0.3 。随着坯体数增加，CPLEX在短时间内得不到算例精确解的可能性增加。本实验中将CPLEX 的求解时间上限设为3 600 s，运用IGA 对每个算例独立求解15 次，记下每次求解所得目标函数值与耗时。此外，引入求解质量偏差度量指标 G ap 来度量IGA 的求解性能。IGA 对各个算例的 G ap 指标值为

其中，zIGA(π) 是IGA 独立求解算例15 次所得目标函数值的平均值；z*(π) 为CPLEX 求解当前算例所得的最优目标函数值或在求解时长3 600 s 之外所获可行解的目标函数值。

表4 给出IGA 与CPLEX 对上述6 个算例的求解统计结果。其中，State 和Objective 分别表示CPLEX 在求解时限内对当前算例的求解状态和所得最优或可行解的目标函数值；Min、Max、Avg和Sd 分别表示IGA 独立求解当前算例15 次所得目标函数值的最小值、最大值、平均值及其标准差；Time表示IGA 独立求解当前算例15 次的平均耗时。由表4 可知，对n=17 的算例，在独立运行的15 次求解中IGA 多次求得精确最优解，平均耗时仅约为CPLEX 求解平均耗时的1/700；对n∈{18, 19, 20, 21,22}的算例，CPLEX 耗时多达3 600 s 仍得不到各自精确解，仅能求出近优解。对n∈{18, 19, 20}的算例，IGA 不仅能达到与CPLEX 相同的算例求解质量 (Gap 值均为0.00)，且平均用时约为CPLEX 求得近优解所耗时间均值的1/1 200，多次运行所得解的质量稳定性也较高。对n∈{21, 22}的算例，在平均耗时不到4 s 的前提下IGA 在15 次独立运行中所得最差解比CPLEX 所得近优解的质量更优，对应 G ap 值均在-0.5%以下。综上，IGA 对6 个测试算例所得解的质量可达到或优于在限定3 600 s 运行时间下CPLEX 所得解的质量，且求解用时极短，体现出IGA 对IOPDSP 的求解有效性。

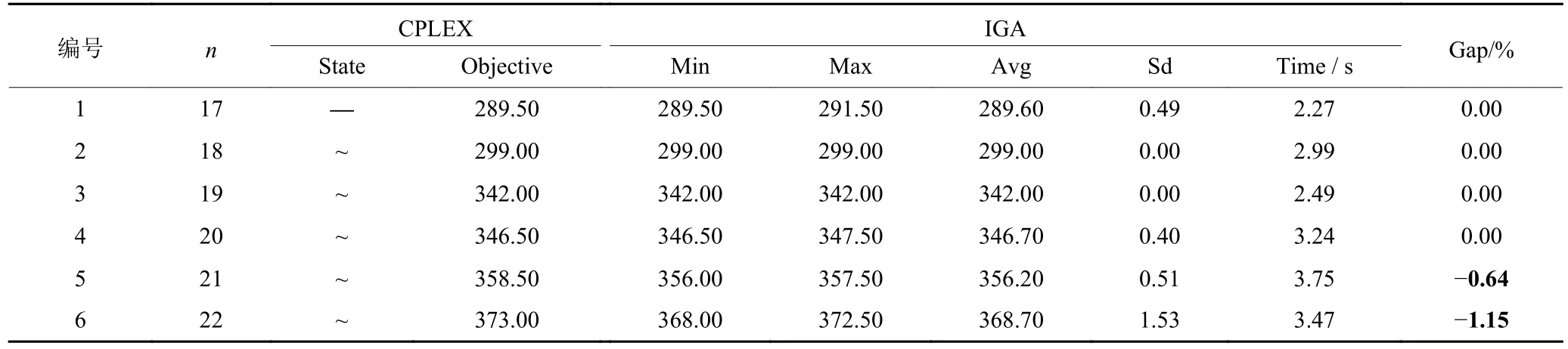
表4 IGA 与CPLEX 的算例求解统计结果1)Table 4 Solution results of IGA and CPLEX over test instances

3.3 基于实例的灵敏度实验分析

本节利用灵敏度实验法探析特定场景下可控因素的变化对实例中陶瓷企业作业运营总成本 T C 产生的影响，以降低 T C 为目标对可控因素的取值或决策给出建议。鉴于IGA 对IOPDSP 的求解有效性，运用IGA 对实例中可控因素的灵敏度进行研究。实例中坯体的总数、尺寸和内部烧制时间，电窑炉的容量和额定功率，合约商对坯体的外包索价确定后再发生变化的可能性很小，故它们属于不可控因素。坯体外包总成本预算G、单位时间上坯体批加工成本 λ 和单车次分批配送成本 µ 分别会因企业经营与融资状况、用电分时选择方案和选用车型的不同而出现取值上变化，故它们是实例中可控因素。G与 η 之间成正比关系，故外包总成本预算状况会反映在η的取值上。λ 与 δ 之间成正比关系。根据当地工商业分 时 用电 政策 规定①《山东省发展改革委员会完善工商业分时电价政策的通知 (鲁发改价格〔2021〕986 号) 》， δ 的可 能值 有0.5、1.0 和1.5，分别对应烧制时间在用电低谷期、平时期和高峰期的情况，故 λ ∈{1.5,3.0,4.5} 。单车次配送成本µ由选用车型的最大载荷量Q2决定。3PL 公司提供9 种配送车型，最大载荷量从40 m3到80 m3不等，相邻车型的最大载荷量相差约5.0 m3。

下 面考察 η 、 λ 和 µ 取 值变化对 T C 的 影响。经预实验发现，当 η ＜0.1 时坯体外包所带来的降本效果很小；当 η ＞0.8 时 η 值的变化也基本不会对 T C 产生影响。本实验中设定 η 的有效观测区间为[0.1, 0.8]，观测浮动步长为0.05，观测点有15 个。为区分作业外包总成本预算特征，将 η 的有效观测区间划分为3 段：[0.1, 0.3]； (0.3, 0.5]； (0.5, 0.8]，分别对应外包总成本预算的高度紧张、中度紧张和充足状态。本实验针对实例的以下两种场景而展开。

场景1受经销商紧急催货或配送车型可用性动态变化等情况所限，陶瓷企业不得不将坯体烧制时间安排在用电高峰期。因此时烧制成本高昂，该企业迫切希望通过安排一部分坯体外包或优选配送车型而使 T C 下降。

场景2陶瓷企业因现金流状况不佳，融资能力不足，导致对坯体外包总成本的预算高度紧张，亟待通过灵活安排内部电窑炉的烧制时间，选用合适的配送车型而使 T C 下降。

在 面向 场景1 的 灵敏 度 实验 中，取 λ =4.5 ，面向不同的 ( η,µ) 取 值组合观测IGA 求得的 T C 值。由于 η 的有效观测区间内有15 个观测点和9 种可选车型， ( η,µ) 取 值组合共计1 5×9=135 种。在每种(η,µ)取值组合下IGA 独立求解实例15 次，并统计这15次所得目标函数值的均值。图4 给出135 种 ( η,µ) 取值组合下分别运用IGA 所得的 T C 均值。由图4 可得如下结果。

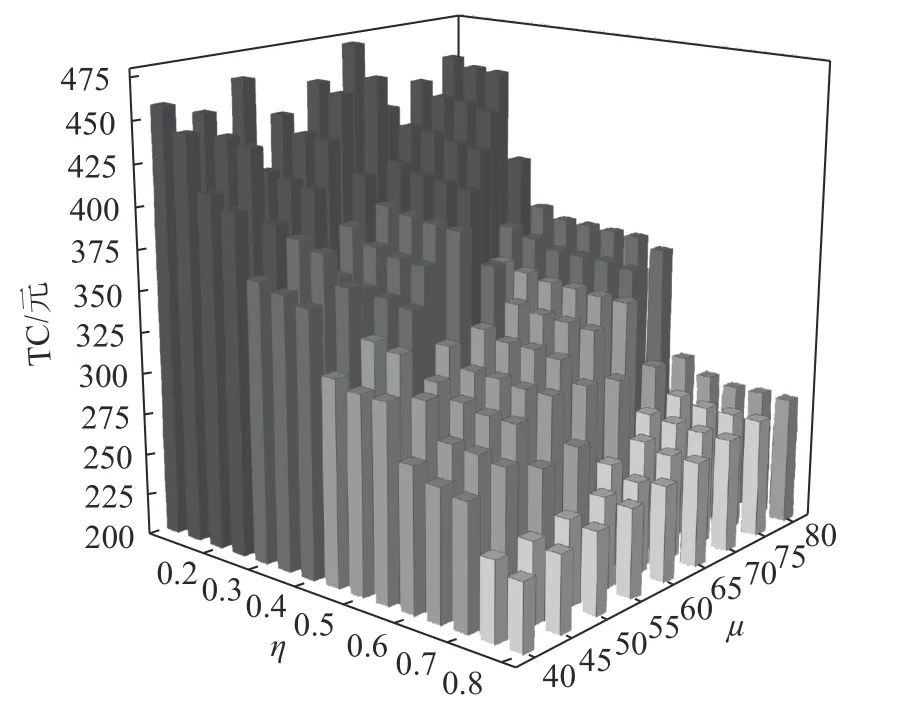
图4 135 种 ( η,µ) 取值组合下的 T C 均值Figure 4 Means of TC using 135 combinations of (η,µ)

1) 不同的 ( η,µ) 取 值组合下 T C 的均值有明显差异。图中显示的最高 T C 均值为474.8 元，出现在(η,µ)的 取值组合 ( 0.1,65.0) 下 ；最低 T C 均值为242.4元，出现在 ( η,µ) 的 取值组合 (0.8, 40.0) 下，最高TC均值约为其最低均值的1.96 倍。

2) 在 η 取值相同的情形下， µ 的不同取值对TC 有一定影响。当外包总成本预算处于紧张状态时(η≤0.5)，该影响的显著性增强；但在整体上难以直观确定使 T C 下降效果相对更好的配送车型。

3) 在 µ 取值相同的情形下， η 的不同取值对TC的影响更明显，并在有效观测区间内随着 η 值的按步长浮动增加， T C 逐渐下降。

4) 建议该企业在场景1 下通过融资、贷款等手段尽量增加外包总成本预算，使 η 值不小于0.75。

为验证上述现象是否有统计学意义，以 T C 为因变量， η 和 µ 为自变量，对场景1 下收集的灵敏度实验数据进行双因素方差分析，结果如表5 所示。其中， η 和 µ 组 成交互项的p值显示为0.00，认为不同(η,µ)取 值组合下 T C 的差异有统计学上显著性，从图4的结果1) 得以证实； η 和 µ 各 自单项的p值都显示为0.00，但 η 对应的F值远大于 µ 对应的F值；可见相较于 µ ， η 对 T C 的影响显著 性更高，从图4 的结果2) 和3) 得以证实。

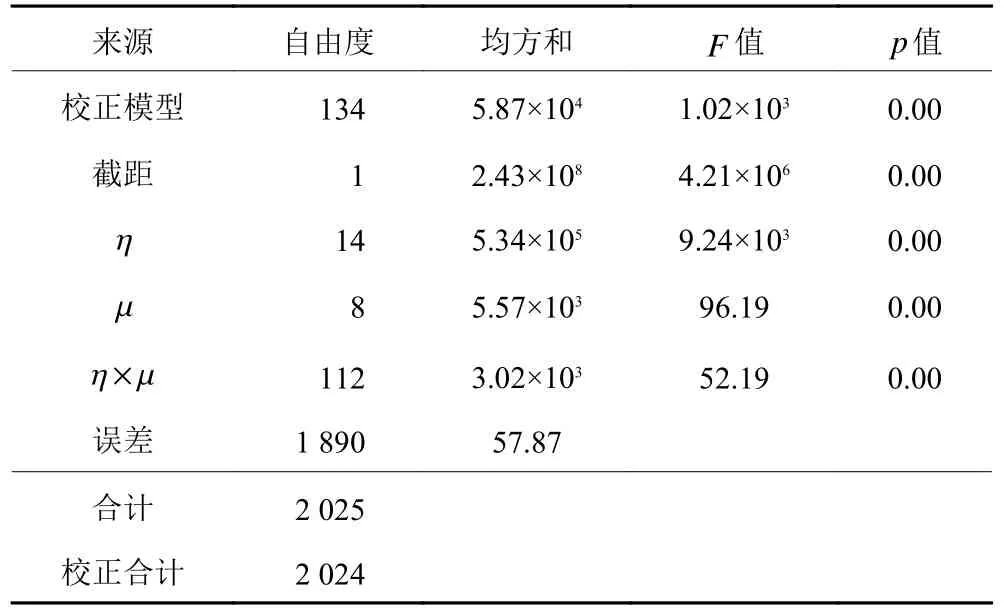
表5 对场景1 下实验数据的双因素方差分析结果Table 5 Two-factor ANOVA results using experimental data in Scenario 1

在 面向 场景2 的 灵敏 度 实验 中，取 η =0.2 ，面向不同的 ( λ,µ) 取值组合观测IGA 求得的 T C 值。由于分时用电价格系数的3 种选项和可选的9 种车型， ( λ,µ) 取值组合共计 3 ×9=27 种。在每种 ( λ,µ) 取值组合下IGA 独立求解实例15 次，并统计这15 次所得目标函数值的均值。图5 给出27 种 ( λ,µ) 取值组合下分别运用IGA 所得的 T C 均值。由图5 可发现以下4 个结果。

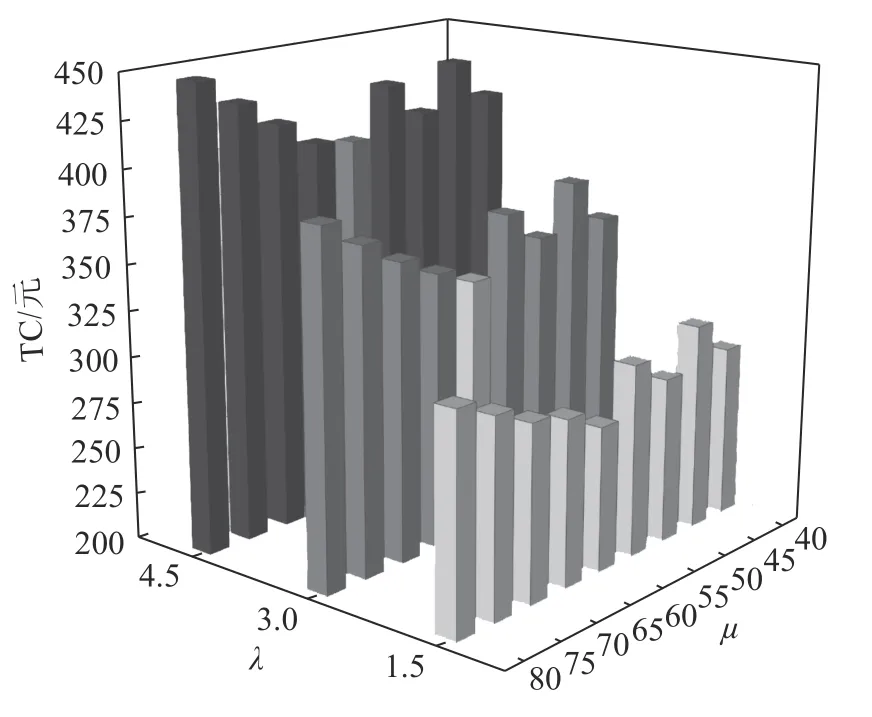
图5 27 种 ( λ,µ) 取值组合下的 T C 均值Figure 5 Means of T C using 27 combinations of(λ,µ)

1) 不同的 ( λ,µ) 取值组合下 T C 的均值存在差异。图中显示的最高 T C 均值为449.0 元，出现在(λ,µ) 的取值组合 ( 4.5,80.0) 下 ；最低 T C 均值为278.5元，出现在 ( λ,µ) 的取值组合 ( 1.5,60.0) 下 ，最低TC均值约为其最高均值的62.03%。

2) 在 λ 取值相同的情形下， µ 的不同取值对TC有 明 显 影 响。当 µ =60 时 该 企 业 在 T C 上 取 得 相 对 更好的下降效果，故不建议在场景2 下选用最大载荷量与60 m3相差过大的车型。

3) 在 µ 取值相同的情形下， λ 的不同取值对TC的影响更加明显。坯体的内部烧制时间安排在用电平时期和低谷期所耗 T C 均值比安排在用电高峰期分别下降13.93%和29.17%，故建议该企业在场景2 下把坯体烧制时间安排在用电非峰时段。

4) 当把坯体烧制时间安排在用电低谷期时，通过优选配送车型可使 T C 进一步下降。从3PL 公司选用Q2= 6 0 m3的车型比选用Q2= 8 0 m3的车型在TC值上会下降12.15%。

为验证上述现象是否有统计学意义，以 T C 为因变量， λ 和 µ 为自变量对场景2 下收集的灵敏度实验数据进行双因素方差分析，结果如表6 所示。其中， λ 和 µ 组 成交互项的p值显示为0.00，认为不同的 ( λ,µ) 取值组合下 T C 的差异具有统计学上显著性，从图5 的结果1) 得以证实； λ 和 µ 各 自单项的p值都显示为0.00，但 λ 对应的F值远大于 µ 对应的F值，可见 λ 对 T C 的影响显著性比 µ 更高，从图5 的结果2) 和3) 得到验证。

表6 对场景2 下实验数据的双因素方差分析结果Table 6 Two-factor ANOVA results using experimental data in Scenario 2

4 结论

本研究关注p-batch 模式下单机差异尺寸作业外包、生产与配送联合调度问题 (IOPDSP)，为其构建0-1 规划模型，并依赖问题特征设计出改进型遗传算法 (IGA)。利用来自某陶瓷企业的IOPDSP 测试算例，对比分析了IGA 与CPLEX 软件的求解表现。结果表明，IGA 所得解的质量不低于CPLEX 在3 600 s 时限内所得解的质量，且求解耗时小于4 s。而后，运用IGA 针对IOPDSP 实例分场景开展灵敏度实验分析，围绕外包总成本容许率、分时单位电价和配送车型三因素探究取值变化对作业运营总成本 T C 的影响，得出以下主要结论。

1) 当陶瓷企业将坯体烧制时间安排在用电高峰期时，相较于配送车型的变化，外包总成本容许率的变化对 T C 的影响更显著。建议企业通过融资或贷款等手段努力增加外包总成本预算。

2) 当陶瓷企业的外包总成本预算处于高度紧张状态时，分时单位电价和配送车型上的变化都对TC有显著影响，前者的显著性更高。建议企业将坯体烧制时间安排在用电非峰时段，优选最大载荷量为60 m3的车型承担制成品分批配送任务。