基于可变需求的EPQ 与视情维修联合优化

杨晓梅，白 钰

(太原科技大学 经济与管理学院，山西 太原 030024)

生产计划作为企业经营计划的重要组成部分，是企业对生产任务作出统筹的安排。Taft[1]首次提出侧重于库存式生产的经济生产批量，其假设在整个生产过程中设备一直处于完美的运行状态，不会劣化至发生故障，并且生产的产品质量全部合格。然而，在实际的生产过程中，设备的可靠性随着使用时间逐渐降低，故障率和不合格品率不断增大，需要对设备进行维修活动[2]，保证设备的正常运转。但若只考虑维修计划，会对生产进程造成影响，使设备的有效运行时间达不到预期，发生延迟交货的情况，导致客户满意度下降。因此，有必要进行经济生产批量与设备维修的联合决策研究。

考虑到设备维修和生产计划之间的相关性，学者们首先进行了基于时间的预防性维修与经济生产批量的集成研究。如Chelbi 等[3]考虑故障停机对经济生产批量和周期性预防性维修的联合决策产生的影响。Suliman 等[4]为了降低生产过程从受控状态转换到失控状态的概率，定期对设备进行预防性维修。卢震等[5]和Nourelfath 等[6]分别建立单机环境下单产品和多产品的经济生产批量与周期性不完全预防性维修集成优化模型。Fitouhi 等[7]提出非周期性预防性维修和经济生产批量问题的联合策略。上述研究往往是采用基于时间的预防性维修策略，这一策略在实际运用过程中没有考虑设备个体间的差异，可能会导致维修不足或维修过剩。随着传感器技术的发展，使得视情维修策略在设备管理中得以应用。近年来，学者开始进行经济生产批量和视情维修的集成研究。Jafari 等[8]利用比例风险模型对设备的可靠度进行分析，以经济生产批量和预防性维修阈值为决策变量构建了生产和维修的联合优化模型。Peng 等[9]通过连续监测设备的劣化状态，建立基于状态的维修和EPQ (economic production quantity，经济生产批量) 的联合优化模型。郑睿等[10]分析生产过程失控、故障率和故障停机时间对生产和维修联合决策的影响。Abdelhakim 等[11]针对单产品的生产系统的维修策略进行研究，设定在一个生产周期内定期对设备检测，当劣化水平超过维修阈值则停止生产并实施相应的维修。成国庆等[12]在一个批量生产结束后对设备状态以及产品质量进行检测，根据检测到的信息决定维修活动。刘勤明等[13]基于时间延迟理论描述了不同的故障类型，建立多类型维修和经济生产批量联合优化模型。方叶祥等[14]针对实际生产中设备劣化及产品返工的情况寻求最佳生产批量。刘学娟等[15]将设备劣化问题与EPQ 联合研究，运用随机系数回归模型描述设备的劣化状态，并且选择加速失效时间模型分析协变量的影响。

上述研究通常假设生产需求是固定的，但是，在实际生产过程中，由于生产环境、设备使用条件等不确定性，生产需求往往会随着销售价格、时间和产品质量而变化，因此，有必要研究可变需求下经济生产批量与设备维修的联合决策。本文针对可变需求下的经济生产批量与视情维修联合决策问题，设计周期性状态检测的维修策略，根据此策略建立单位时间平均利润最大化模型，通过对模型进行求解，可得到最优的检测间隔期和预防性维修阈值，从而确定最优经济生产批量。

1 符号定义及相关假设

1.1 符号定义

本文相关的符号定义如表1 所示。

表1 符号说明Table 1 Notation description

1.2 相关假设

1) 产品的生产率p恒定；

2) 产品的价格在一个生产周期内不发生变化；

3) 考虑设备状态的检测费用，检测时间忽略不计；

4) 设备在“受控”“失控”状态下均会产生一定比率的不合格品；

5) 在生产过程中一旦发现不合格品，对其进行修复，修复时间忽略不计。

2 问题描述

本文考虑的是单设备生产系统，该设备以生产率p进行产品的生产，产品的需求率为d(p＞d) 。生产过程中，设备随着运行时间的增加会发生劣化直至故障，当劣化状态水平低于故障后维修阈值，设备处于受控状态。当劣化状态水平达到或高于故障后维修阈值，设备转换为失控状态。两种状态下均会生产出不合格品，但相比而言，在失控状态下会产出更多的不合格品。由于设备问题直接影响了产品的质量水平，为了提升产品质量水平，就需要提高设备可靠性，因此在一个生产周期内对设备状态进行检测，根据所检测到的设备所处劣化水平实施相应的维修活动，包括预防性维修和故障后维修，两种维修活动都保证设备修复如新。一旦设备进行维修，生产过程就结束，完成批量为Q的产品的生产，之后以需求率d消耗库存，若设备维修花费的时间小于库存消耗的时间，在库存消耗完毕后开始下一更新周期的生产；若设备维修的时间大于库存消耗的时间则会产生缺货，维修结束后再进行下一更新周期的生产。

根据上述策略，库存水平和维修活动的对应关系可分为两种情形 (如图1 所示)。其中，X(t) 为设备在t时刻的劣化状态水平，I(t) 为库存水平；•表示检测点。

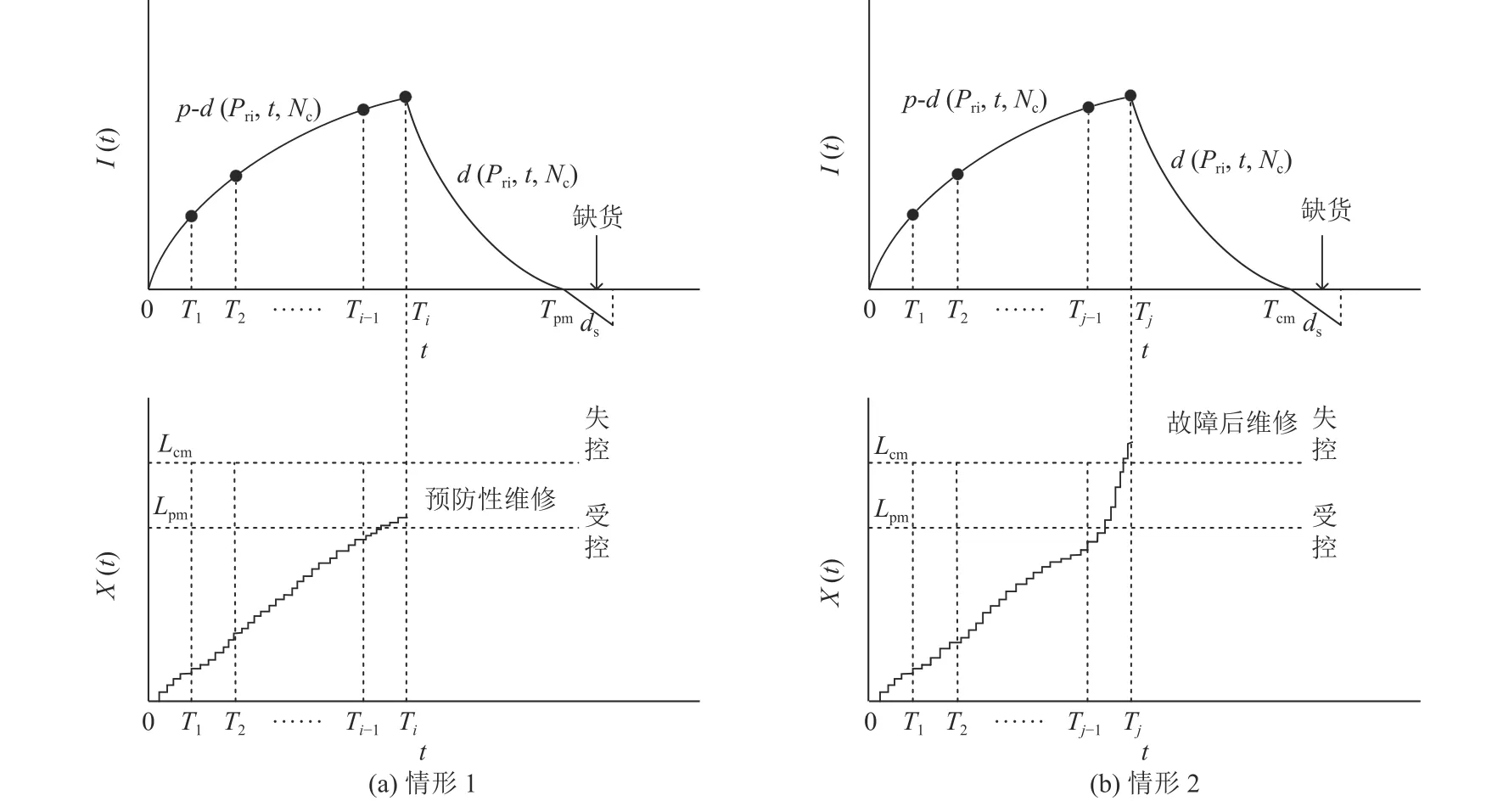
图1 各情形的示意图Figure 1 The example of each scenario

情形1在一个生产周期内每隔时间T对设备进行检测，在检测点Ti(i=1,2,3,···) 发现设备劣化水平达到或超过预防性维修阈值Lpm，立即进行预防性维修，如图1 (a) 所示。

情形2在一个生产周期内每隔时间T对设备进行检测，如果设备劣化水平达到或超过故障后维修阈值Lcm，设备仍然劣化运行，直到在检测点Tj(j=1,2,3,···)被检测出来，立即进行故障后维修，如图1 (b) 所示。

3 模型建立

以单位时间平均利润最大化为目标构建联合优化模型，其中将两次设备开始生产之间的时间间隔定义为一个生产周期，根据更新报酬理论[16]，可以利用一个生产周期的单位平均利润来代替整个生产计划期内的单位平均利润，一个生产周期的单位时间平均利润为生产周期的平均利润E(Pro) 除以生产周期的平均时长E(Tc) ，即

式 (1) 中，平均利润为平均总收入减去平均总费用，产品销售价格乘以平均生产批量得到平均总收入，总费用包括生产准备费用、不合格品返工费用、库存持有费用、检测费用、维修费用、缺货费用。

根据所设计的联合策略可知，通过检测设备劣化的状态，对设备进行预防性维修或故障后维修两种维修活动。Gamma 过程可描述连续且单调递增的随机过程，适用于刻画设备的劣化现象。本文利用此过程来描述设备的劣化进程。设X(t) 为 设备在t时刻的劣化状态水平，且X(0)=0 ， 形状参数为 γ ，尺度参数为 η ，概率密度函数

下面对一个生产周期内两种情形下的平均费用和平均时长进行描述。

3.1 情形1

该情形用S1表 示，即当Ti时刻对设备进行检测时发现设备劣化水平达到或超过预防性维修阈值Lpm，对设备进行预防性维修，该情形发生的概率为

该情形发生时产生的费用包括生产准备费用、不合格品返工费用、库存持有费用、检测费用、预防性维修费用、缺货费用。

1) 生产准备费用。

由于生产启动前会产生各种准备工作的费用，则平均生产准备费用为

2) 不合格品返工费用。

该情形下的生产运行平均时长为

在这种情形下，设备始终处于“受控状态”，“受控状态”下产生不合格品的比率为 α1，则平均不合格品数为

为了提升产品的质量，减少不合格品的产生，在不合格品流入市场后采取召回措施将其进行返工，产生相应的返工费用。设定单位不合格品返工费用为Cr，因此产生的平均不合格品返工费用为

3) 库存持有费用。

考虑到需求会随时间的推移发生变化，本文针对需求随时间指数增长的产品。根据需求定律可知，产品的需求量和价格呈反比关系，即随价格上升，产品的需求量会减少；反之，产品的需求量会增加。同时，由于客户的需求与产品的质量水平也相关。因而，产品的需求率受时间、销售价格和生产的不合格品数3 个因素的影响，本文构建了产品需求率函数模型如式(8)所示。

其中，dmax是不受任何因素影响的最大需求；a、b、λ为需求率对价格、不合格品数和时间的敏感系数，a，b，λ＞0 。

令库存水平用I(t) 表示，由式 (8) 可以得到库存水平I(t) 的微分方程为

根据条件I(0)=0,I(Tpm)=0 ，求解微分方程得到

利用I(t) 在t=Ti的连续性可得库存消耗完的时刻为

根据式 (10) 、式 (11) 可知，在该情形下一个生产周期内的平均库存持有费用为

4) 检测费用。

该情形下，由于在Ti时刻设备会停机进行预防性维修，因此设备状态的检测次数为i次，则平均检测费用为

5) 预防性维修费用。

当在检测点Ti发现设备劣化水平达到或超过预防性维修阈值，立即进行预防性维修活动，产生的平均预防性维修费用为

6) 缺货费用。

当设备预防性维修时间ypm超过库存的消耗时间Tpm-E(Ti)，则会出现缺货，在缺货期，客户的需求是一个常数ds，缺货费用为缺货数量乘以单位产品单位时间内的缺货费用Cs，因此平均缺货费用为

由此可得到情形1 的平均总费用E(C|S1) ，即

该情形下一个生产周期的平均时长为

3.2 情形2

该情形用S2表示，即设备在Tj-1时刻的劣化水平低于预防性维修阈值，而在Tj时刻检测到劣化水平达到或超过故障后维修阈值Lcm，对设备采取故障后维修，该情形发生的概率为

该情形发生时产生的费用包括生产准备费用、不合格品返工费用、库存持有费用、检测费用、故障后维修费用、缺货费用。

1) 生产准备费用。

2) 不合格品返工费用。

当劣化状态水平X(t)＞Lcm，设备处于“失控状态”，“失控状态”下产生不合格品的比率为 α2，根据式 (2) 可得，设备从初始状态0 到达某一状态x的时间tx的分布函数为

则生产期间产生的平均不合格品数为

可得平均不合格品返工费用为

3) 库存持有费用。

该情形下的生产运行平均时长为

同样由式 (8) 可得库存水平I(t) 的微分方程为

根据条件I(0)=0,I(Tf)=0 可以得到库存函数

利用I(t)在t=Tj的连续性得到库存消耗完的时刻为

根据式 (25) 、式 (26) 可知，在该情形下一个生产周期内的平均库存持有费用为

4) 检测费用。

对设备状态进行j次检测产生的平均检测费用为

5) 故障后维修费用。

当在检测点Tj发现设备劣化水平达到或超过故障后的维修阈值，实施故障后维修活动。鉴于实际设备维修时的故障后维修费用往往比预防性维修费用更高，因此该情形下产生的平均故障后维修费用为

6) 缺货费用。

当设备故障后维修时间ycm超过库存的消耗时间Tcm-E(Tj)，会出现缺货，因此产生的平均缺货费用为

由此可得该情形下的平均总费用E(C|S2) ，即

该情形下一个生产周期的平均时长为

综上所示，一个生产周期内的平均总费用为

一个生产周期的平均总时长为

由此，以单位时间平均利润最大化作为目标，根据式 (1) 、式 (33) 、式 (34)，可得目标函数为

在上式中，根据对两种情形下的分析可知，预防性维修阈值Lpm、设备状态检测间隔期T这两个变量的变化会影响目标函数值，因此将Lpm和T作为所构建模型的决策变量，对应的约束条件为

4 数值实验

4.1 数值仿真

假设某设备的劣化过程服从 γ =0.6，η=0.8 的Gamma 分布，设备处于“受控状态”下产生的不合格品比率 α1=0.03 ，设备处于“失控状态”下产生的不合格品比率α2=0.3 ，故障后维修阈值Lcm=9 ，预防性维修时间和故障后维修时间服从指数分布F(t)=1-e-0.8t和F(t)=1-e-1.6t，该设备的生产率p=300 件/d，最大需求dmax=180 件/d，产品销售价格Pri=30元/件，其他参数值如表2 所示。

表2 相关参数值Table 2 Related parameters

遗传算法作为优化算法之一，具有隐含并行性和全局搜索的特点，适用于求解各类离散、连续优化问题，被广泛应用于工业设计、生产管理、交通运输等领域。鉴于此，本文引入遗传算法进行模型的求解。根据式 (36) 中各决策变量的取值范围，采用实数编码的方法，设定种群规模为50，迭代次数为100，交叉概率为0.8，变异概率为0.2，进行50 次仿真实验，可得到最优解为单位时间平均利润=6 547.2元/d，对应的最佳决策方案为检测间隔期T∗=2.325 d ，预防性维修阈值=6.997 。单位时间平均利润Pro随检测间隔期T和预防性维修阈值Lpm的变化如图2 所示。

图2 Pro 随T，Lpm 的变化Figure 2 The variation of Pro with T and Lpm

由图2 可以看出，当T或Lpm不变时，单位时间平均利润Pro随着预防性维修阈值Lpm或检测间隔期T先增大后减小变化。这是因为Lpm或T较小时，虽然生产周期内的平均总费用减少，但也导致平均生产量降低，使企业平均总收入的下降幅度大于平均总费用；而当Lpm或T较大时，虽然平均生产量的增加使平均总收入升高，但由于设备故障概率的增加，会产生过高的故障后维修费用，使平均总费用的增长速率高于平均总收入。

为了更好地验证本文策略的可行性，将本文的EPQ 模型和基于固定需求的EPQ 模型分别与视情维修联合决策所得到的仿真结果进行对比，基于固定需求的模型记为模型1，在建立模型1 时，考虑需求不受任何因素影响，即设定需求d=dmax=180件/d，表3 列出了两种模型的最优结果。

表3 模型1 和本文模型的最优结果Table 3 Optimal results of model 1 and the proposed model

根据表3 可以看出，本文模型与模型1 相比，检测间隔期减小，预防性维修阈值增大，进而使单位时间平均利润增大，因此本文所提出的策略能够使企业有效节约成本，提高利润。

4.2 敏感性分析

为了了解此模型中最优决策变量和最优目标值对相关参数的敏感程度，通过逐一改变相关参数值来寻找最优决策变量和最优目标值受其影响变化的规律。分析的参数包括维修相关参数和需求相关参数，通常设定参数变化的幅度为 - 50%∼50% 。

首先，针对维修相关参数对最优决策变量和最优目标值的影响进行分析，分析结果如表4 和图3所示。

图3 维修相关参数变化对最优决策变量和最优目标值的影响Figure 3 Impact of changes in related maintenance parameters on the optimal decision variables and the optimal objective values

表4 维修相关参数的分析结果Table 4 Analysis results of related maintenance parameters

由表4 和图3 可知，维修相关参数对最优解的影响如下。

1) 随着单位检测费用Cin的增加，增加最优检测间隔期T以减少检测次数，进而降低检测总费用，但导致设备发生故障的概率增加，因此降低最优预防性维修阈值Lpm以减小设备故障的概率。

2) 随着单位返工费用Cr的增加，由于设备在失控状态下产生不合格品的比率高，逐渐降低最优检测间隔期和预防性维修阈值以减小设备故障的概率。

3) 随着单位预防性维修费用Cpm的增加，逐渐增加最优检测间隔期T和最优预防性维修阈值Lpm以减小设备进行预防性维修的概率和费用。

4) 与单位预防性维修费用Cpm的情况相反，随着单位故障后维修费用Ccm的增加，逐渐降低最优检测间隔期和最优预防性维修阈值以增加实施预防性维修的概率，减少设备发生故障的概率和费用。

其次，针对需求相关参数对最优决策变量和最优目标值的影响进行分析，分析结果如表5 和图4所示。需求相关参数对最优解的影响如下。

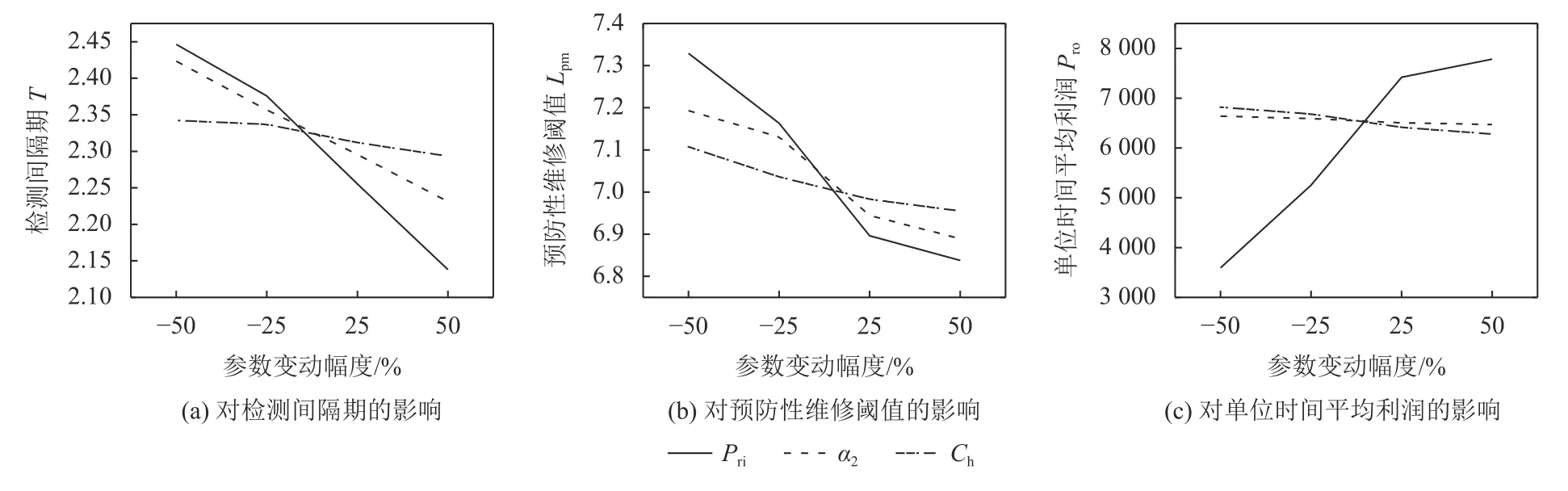
图4 需求相关参数变化对最优决策变量和最优目标值的影响Figure 4 Impact of changes in related demand parameters on the optimal decision variables and the optimal objective values

表5 需求相关参数的分析结果Table 5 Analysis results of related demand parameters

1) 随着单位产品销售价格Pri的增加，产品的需求减少，逐渐降低最优检测间隔期T和最优预防性维修阈值Lpm以减少产生的库存总费用，而单位时间平均利润随之大幅度增加。

2) 随着失控状态下产生不合格品比率 α2的增加，失控状态下产生不合格品的数量增加，因此逐渐降低最优检测间隔期T和最优预防性维修阈值Lpm以减小设备故障的概率。

3) 随着单位库存持有费用Ch的增加，逐渐降低最优检测间隔期T和最优预防性维修阈值Lpm以缩短生产周期，减少库存的持有总费用。

5 结论

本文进行了可变需求下的经济生产批量与视情维修联合优化研究，其中需求率取决于3 个因素：销售价格、时间和不合格品数。运用Gamma 过程描述设备的劣化过程，根据检测到的设备劣化水平确定维修行为，包括预防性维修和故障后维修。基于更新回报定理建立单位时间平均利润最大化模型。利用遗传算法对该模型进行求解，得到最佳的决策方案。本文研究可辅助企业进行生产和维修决策，使企业能够更加持久稳定地发展。随着制造业的高质量发展，为了满足客户的多样化需求，以后的研究可以扩展到针对多设备生产系统的生产和维修的联合决策研究。