一种基于压缩感知的WSN 节点多目标定位实现方法

张雪峰

（1.广州番禺职业技术学院，广东 广州；2.Nueva Ecija University of Science and Technology, Cabanatuan City Philippines）

引言

随着传感器网络的发展，一些学者提出了压缩感知理论[1-2]，它在稀疏矩阵信号图像处理中起着重要的作用。压缩感知理论以稀疏矩阵信息的测量值和重构算法作为恢复复杂图像信息的基础和手段[3]。无线传感器网络的完整性在一定程度上受到限制。考虑到网络中定位信息的不完备性，其监测区域划分为若干小网格区域进行分析，各个节点和位置目标随机分布在每一个位置网格中。现在以目标位置信息作为向量生成一种新的基于压缩感知的多目标定位方法，以满足重构定位算法的要求[4]。针对定位测量的不完备性，提出了一种基于压缩感知的无线传感器网络多目标定位方法，进一步提高了传感器网络的监测能力，得到了一种新的基于压缩感知的无线传感器网络多目标定位计算方法。

1 节点构成与特征向量

1.1 WSN 的网格构成

无线传感器网络是在传感器网络飞速发展的历史时刻应运而生的，它由大量的传感器子节点组成。同时，这些传感器节点具有相应的功能，包括无线通信、数据采集和数据处理。它们的功能也是多样而有效的，例如感知、收集和处理网络覆盖区域内感知对象的信息。传感器网络的组成包括传感器节点、汇聚节点和管理节点三部分。

1.2 WSN 的网络特征

无线传感器网络具有一定的特征。

第一，如果没有将无线传感网络的中心定位提前设定，那么其中所有节点的地位都是一样的；同时，在这个过程中应用到了多节点定位的分布式算法，各个节点通过这一算法进行相互之间的协调，发挥其能动性并组织成一个测量网络。

第二，无线传感器网络中的节点具有相应的特征，节点的体积是非常小的，所以其可以存储和携带的能力是非常有限的。外界环境能够对其产生一定的影响，在这种情况之下，导致电池不能随意地更换，对于无线传感器网络来说，降低电池能量的消耗是一个重要的课题。

第三，在无线传感器网络中存在着大量的节点，其密集地分布于传感器网络中。

1.3 网络模块组成

在众多节点构成了无线传感器网络中，节点构成分成了几个部分，包括数据采集模块、数据处理、通信模块等。节点在无线传感器网络中被分成了两类，分别是传感器节点和汇聚节点。传感器节点将传感器作为手段和方法，对检测区域中的众多物理量进行测量；同时，传感器节点还具有自动组成网络的功能。汇聚节点能够将不同的传感器网络连接起来，将传感器节点发送过来的相关信息在上位机上显示出来。

传感器节点的特点包括能量消耗少、节点微小等，相应的设备对其计算和存储的能力进行了一定地限制。一个与上位机连接起来的基站节点和众多的传感器节点构成了无线传感器网络。基站节点处在能量消耗低的一个状态，传感器节点先是将相应的请求发送给基站节点，然后进入低功耗的状态。

1.4 数据采集与传输

无线传感器网络有着很重要的作用，对目标区域的数据进行采集和传输。在科学的发展过程中，传输的技术也是发展的越来越快，实现了更多的突破，传感器网络自动组织的功能越来越强，所应用的范围随之不断拓展。在传感区域中有大量的节点分布开来，利用一定的方式和途径将传感器采集到的数据传输到处理中心。然后，实现了传感器网络存储的功能，也导致了电池供电能力的不足，那么，在这种情况之下，提高无线传感器网络的数据存储能力是非常有必要的。

1.5 现有问题的提出

无线传感器网络节点所具有的功能是十分强大的，对矩阵向量信息进行一定的分析和处理。不过，传感器节点也有着一定的不足和缺陷，它的尺寸和复杂程度不利于传感器网络的数据存储、计算等。在这个基础上，提出了压缩感知的理论，解决了其中存在的问题。

2 网络模型与参数定义

2.1 信息节点与网格

静态无线传感器监测网络具有位置信息节点，可以随机部署。网络部署后，位置信息节点不会移动；然后，监控目标也处于静态。将监测区域划分为N 个网格，在网格中随机部署M个位置信息已知的传感器节点。在K 个目标中，而每个网格中最多有一个目标。假设目标的实际位置是网格的中心坐标，稀疏矩阵矢量位置随时间的分布如图1 所示。

图1 传感节点随时间分布情况

2.2 信号向量的重构

（1） 假设K 个被监控目标的位置为所在网格的中心坐标，将目标位置信息向量定义为s，s 是N*1 的向量，在监控区域中所有的目标数为K，那么，在s 中，只有K 个元素为1，剩下的元素都是0。

（2） 假设Ψ 是一个N*N 的稀疏矩阵，当某个传感器节点位于i（在1 到N 的范围内）网格中并且感知到了j（在1 到N 的范围内）网格中的目标时，Ψij＝1，否则Ψij＝0。将X 设为X＝{x1，x2，…，xN}T，可以得出：X＝Ψs，这表示的是每个网格中节点感知到的目标数。

（3） 假设在N 个网格中随机部署了M 个传感器节点，并且当M＝0 时，将测量矩阵定义为Φ，矩阵Φ 每一行只有一个元素1，剩下的都是0。那么，在传感器网络部署工作完成之后，它的位置也随之确定下来，也就是说测量矩阵Φ 是确定的。稀疏矩阵的求解过程如图2 所示。

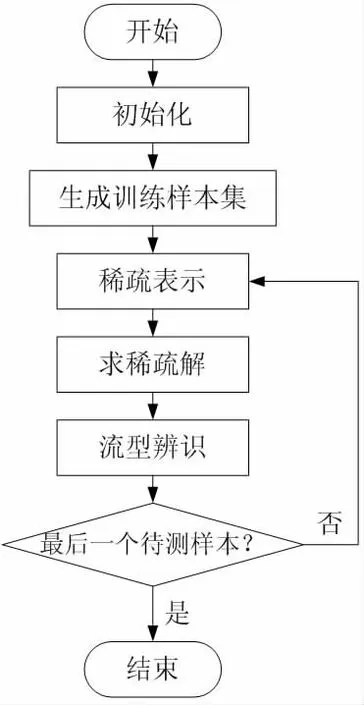
图2 稀疏矩阵的求解过程

（4） 将测量值矩阵用Y＝{y1，y2，…，yM}T来表示，在第i 个传感器节点能够感知到在其感知范围内共有K 个目标时，yi=K（K≤M），那么，这里的测量值矩阵可以用来记录M个传感器节点感知目标的有关情况。

（5） 测量值矩阵可以满足公式：Y=ΦX=ΦΨs=As，可以说建立起了测量矩阵与目标位置信息向量之间的关系，所以，将AM*N作为感知矩阵的公式表达。那么r(A)≤M 且r(A)≤N，即有r(A)≤min{M,N}，r(A)=N；否则，r(A)=M。

3 建立在压缩感知基础上的目标定位方法

与奈奎斯特采样定理相比较，压缩感知理论完成信号采样的过程中产生的频率更低，实现了一定的突破，而且采样的次数也更少，能够更好地重构出原始信号。采用贪婪匹配可以进行多目标定位[5]。在大信息量的采样、处理等方面，压缩感知理论得到了更加充分的应用。

3.1 稀疏信号表示

通过对压缩感知理论的分析，可以了解到，监测网络分为静态和动态两种状态，处于静态时，目标的位置信息s 中只有K 个元素值大于0。重构算法在无线传感器检测网络中发挥着重要的作用，通过稀疏性的含义可以知道，s 是一个稀疏向量，所以，可以通过重构算法将向量进行恢复。网络定位信息的获取过程中，没有必要将节点布置在每个网格中以此来获得矩阵x。网络具有连通的特性，在集中式定位中，以此作为依据，将M个节点值赋予矩阵y、将A 给中心节点，重构获得稀疏向量s。基于ZigBee 或者DASH7 协议验证符合程度[6-8]。

3.2 信号的重构

压缩感知理论的应用过程中，测量矩阵和稀疏矩阵在其中发挥着重要的作用，这两者与信号的重构有着密切的联系，要实现稀疏信号重构的高精度，就必须满足相应的条件，感知矩阵要满足受限等距性条件，可以得到所需要的效果。在多节点协同工作时，协议计算多时间片σ 覆盖路径，计算节点集合及其工作时长[9]。

3.3 估测目标位置

压缩感知稀疏向量重构算法在无线传感器网络多目标定位中发挥着重要的作用，而且应用的效果非常明显。

在目标全覆盖的基础上尽最大可能对关键目标进行多角度监测并延长网络生存周期，利用定位重构算法确定估测目标所在位置向量[10-11]。这样，要输入矩阵Y 与T，在运算的过程中对相关的参数进行更新，实现K 次迭代。在每一次迭代的过程中，选择正交矩阵T 中的列，实现列和当前的冗余向量r0最大程度的关联，然后，把列置为零更新矩阵T，从矩阵Y 中将相关部分减去，继续迭代，出现稀疏度K 方可停止迭代，这就是对稀疏向量s 的重构，也就是估测的目标所在位置。这种重构算法有着鲜明的优势，在目标位置的确立中发挥着重要的作用，它的计算难度不高，所需要的时间相对短，而且，满足了相应的定位要求。

4 仿真结果

在N*N 的目标监控网络区域随机撒播了M个传感器节点，在网络区域中有K 个待定位目标，并且带定位目标的数量小于传感器节点的数量。将监控网络区域划分成了N 个网格，将M个传感器节点随意地分布在网络区域中，将目标的实际坐标假设为网格的中心坐标，每个网格中最多存在一个目标。将节点的感知半径用r 表示，节点和目标的距离比r 小的时候，那么，可以认为节点能够感知到目标的存在。

4.1 定位误差分析

本文对算法的效果进行评定分析，需要对评价指标的普适性进行相应的考察，这里所说的定位误差指的是绝对误差和感知半径的比值。

将网格的数量假设为N=20×20，将传感器节点的数量假设为M=40，将节点感知半径假设成r=14，监控网络的目标K=10，环境的噪声SNR=25 dB。当目标数相同的情况下，噪声和误差成正比例，误差随着噪声的增大而增大；不过，在有噪声和没有噪声的情况之下，误差的值相差不大。

4.2 算法的定位误差

在WSN 中，节点感知半径发生改变，将r/N 设为稀疏矩阵变量，目标数K=10，网格数为N=20×20,30×30,40×40，M=40，SNR=25 dB，将r/N从0.1 到1 变化。可以得出：当r/N小于0.7 的时候，定位误差与之成反比，也就是随着比值的增加而减少；当等于0.7的时候，定位误差的值是最小的；当比值大于0.7 时，误差随之增加。

在r/N小于0.7 的时候，r 的变化是非常小的，将r/N 作为定位误差，则r 值较小时得到的误差是很大的。当r/N大于0.7 的时候，半径的值是比较大的。

4.3 误差影响分析

稀疏度中的函数可以用压缩感知恢复目标的性能来表示，稀疏度表示的是目标个数和网格个数的比值，随着稀疏度的增大，网格中的目标数就会减少。将网格假设为N=20×20，节点数设为M=40，将 的值设为0.7，分别在没有噪声和有不同噪声的环境中，对目标数从1 到40 的误差进行研究。在压缩感知理论的影响之下，目标数随着稀疏度的增大而减少，恢复的稀疏向量就会越接近正确值，定位误差也就越小。当K 小于15 的时候，在不同噪声影响的环境中，目标数越大，误差也就越大。在监控区域不产生变化的情况下，将目标数增大，这样做可以让目标的密度增加，使得定位的误差越小。

4.4 多目标定位的均方误差分析

将固定目标数设定为K=5、10、15，感知半径r=14，节点数从30 到100，网格数设为N=20×20，环境噪声为SNR=25 dB。压缩感知理论中存在一定的特点，所获取的信息随着测量值的增多而增多，对于系数向量的恢复就会越准确，定位的均方误差（mean squared error, MSE）定位的值也会随之减小，仿真结果如图3 所示。

图3 仿真实验均方误差与定为节点变化之间的关系

4.5 小结

本文定位方法的复杂度与压缩感知和传感器节点感知到的目标数量密切相关。同时，在计算复杂度和一致性方面，基于RSS 模型和重建算法的正交匹配追踪算法来恢复目标位置。当定位目标的计算方法以节点感知到的目标个数为测量值时，通过网络可以方便地获取。与基于测距的定位方法相比，该定位方法的硬件成本较低。基于压缩感知的RSS 定位方法能够满足网络误差较小的定位精度要求，更接近目标值。

结束语

定位参数的不完备性是无线传感器网络非测距定位的一个重要特征。将压缩感知理论引入到多目标定位中，提高了多目标定位精度。在压缩感知理论中，测量矩阵、稀疏矩阵和稀疏向量在离散空间的乘积可以表示传感器节点在感知范围内感知到的目标个数。将正交匹配追踪算法应用于稀疏向量重构，得到多目标位置信息。定位信息具有不完备的特点，但是将压缩感知理论、传感器节点感知目标数模型之间作为基础的定位算法打破了这种限制，提高了多目标定位的精度，网络的定位精度也会随着网络中感知节点数的增加而提高。