用A 星算法进行电动汽车快充电桩布局优化分析

常 昊，郭明昊，秦林杰，吴浩民，焦烯奥

（南京工程学院 电力工程学院，江苏 南京）

引言

随着中国经济迅猛发展，中国的汽车保有量在不断增加，由于近年来对环境保护的要求也在不断提高，新能源电动车无疑成了代替燃油车的最佳选择。伴随电动汽车市场的兴起，充电桩及其配套基础设施成为重要需求。因此，相关电动汽车企业在充电桩建设方面投入了大量的资金，许多充电桩被安置在城市内，为电动汽车提供了充足的能源保障。

然而，目前电动汽车充电桩存在着一桩难求、城乡分布不均匀、多桩闲置、技术隐患大、电价不统一等问题，这将严重制约着电动汽车的发展。因此，对充电桩进行优化布局，是推动新能源电动汽车发展的重要举措。

充电桩主要有“快充”和“慢充”两种类型，由于“快充电桩”可以适应市内巨大的交通车流量，我们选取江苏南京市作为研究对象，对市内“快充电桩”分布进行优化布局。我们研究此问题主要使用了“A 星算法”（即“A-star 算法”），根据文献[1]，“A 星算法（也称为A*算法）”是基于“Dijkstra 算法”的一种典型的、启发式的最短路径搜索算法，其本质是从起点开始搜索代价值最小的节点作为下一次搜索的起点，直到搜索到目标节点为止，由于搜索从一开始就保证代价估计值是最小的，最终得到的路径代价值也同样最小。

该算法被广泛运用于最优路径规划等问题，我们将运用它进行南京市新能源电动汽车充电桩的优化布局分析

1 A 星算法

1.1 “Dijkstra 算法”

“A 星算法”的思路来源于“Dijkstra 算法”，这是一种“半启发式搜索路径算法”，以求起始结点与区域中所有其他结点的估价函数来获得最短路径。

根据文献[2]，“Dijkstra 算法”的执行过程定义如下（程序流程如图1 所示）：

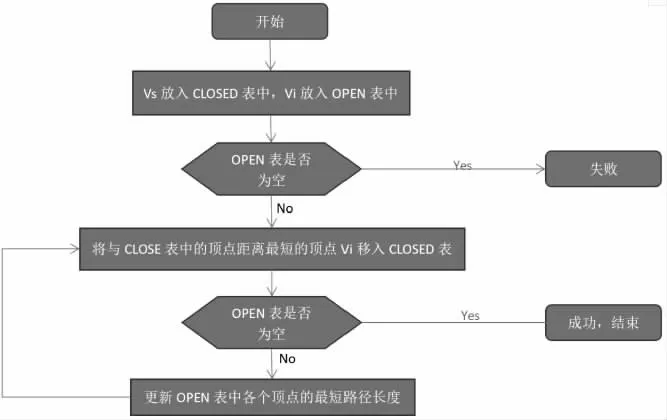
图1 “Dijkstra 算法”程序的流程

（1） 定义名为OPEN 和CLOSED 的两个表；OPEN 用于存放未考察过的结点，CLOSED 表用于存放已考察过的结点。

（2） 假设图中共有n 个结点，选取结点VS 为起点，目标结点为Vi（除VS 的其余结点，i≤n），将起点VS 放入CLOSED 表中，Vi 放入OPEN 表中。

（3） 判断OPEN 表是否为空，为空的话表示搜索过程失败。

（4） 如果不为空的话，计算CLOSED 表中的结点与Vi 的距离，并将距离最短的结点Vi 移入CLOSED 表。

（5） CLOSED 表每加入一个新结点Vi 后要对OPEN 表中各个结点的最短路径长度进行更新。

（6） 跳转到步骤（4），直至OPEN 表为空。

然而，“Dijkstra 算法”以求起始结点与区域中所有其他结点的估价函数获得最短路径，该算法涉及区域大、搜索效率较低，难以适用于多障碍、多线路的复杂最优路径规划问题，因此我们选用根据该算法改良的“A 星算法”。

1.2 “A 星算法”的概念

“A 星算法”在“Dijkstra 算法”的基础上引入了启发函数，加快了算法收敛速度，由文献[2]知道，“A 星算法”是一种启发式搜索算法，即通过评价函数对网格上的点进行价评估来启发式地寻找目标结点，基于最小的代价来寻找通往目标结点最短且最适合的路径。

A 星算法的估价函数如下：

式中：f(x,y)表示当前结点到目标结点的估计距离；g(x,y）表示当前结点到考察结点的实际距离（即既定代价）；h(x,y)表示考察结点到目标结点的估计距离（即估计代价）。

不同于传统的“遗传算法”、“Dijkstra 算法”，此算法的核心是在质点移动的过程中对起始结点到当前结点的既定代价与当前结点到目标结点的估计代价进行实时运算，在网格模型中起止位置间对每一个结点进行目标路径搜索，最终可以得出最优规划路径，因此该方法具有启发性和灵活性。

“A 星算法”寻找路径方式程序的大体思路如图2 所示，其中“OPEN 集合”表示未访问的结点，“CLOSE 集合”表示已经访问过的结点。

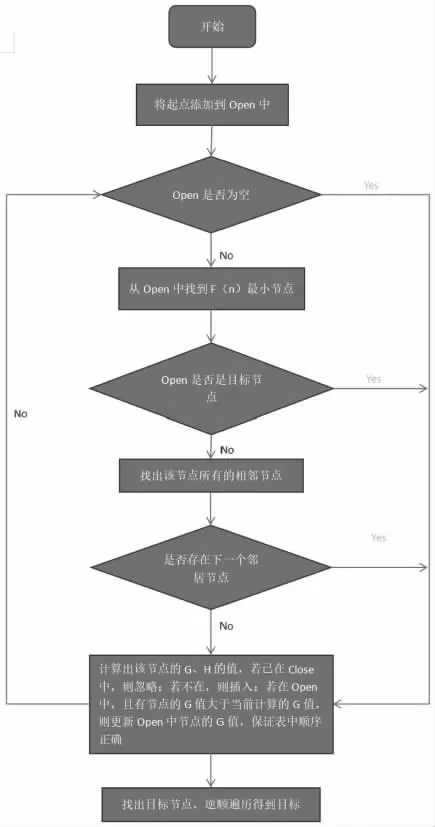
图2 “A 星算法”程序的流程

（1） 我们选定起始点为“START 结点”，从START开始，将该结点首先放入OPEN 集合的列表中。

（2） 对起始点START 的周围结点进行处理，通常在网格图中结点周围有8 个方位，将这8 个方位的父结点设为该“START 结点”，同样放入OPEN 集合的列表中。

（3） 待周围结点全部搜索完毕后，将初始“START 结点”从OPEN 集合中移除，并放入CLOSE集合中。

（4） 先遍历这些预处理的点，判定其是否为“可用结点”（不是障碍结点或不在CLOSE 集合中）。若确定为“可用结点”，则计算那些处理结点的f(x,y)、g(x,y)、h(x,y)值，同时在计算的过程中比较各个结点既定代价、估计代价的大小，每轮循环都将估价函数值最低的结点排在OPEN 集合里面；若确定为“不可用结点”，则将这些结点直接放入CLOSE 集合中。

（5） 若某个处理结点已在OPEN 集合中，检查使用新的路径算出的估价函数是否更低，如果更低，则进行结点更新，并实时调整目标路径，更新时也需要及时调整当前各结点的估价函数大小排序，否则不更新。

（6） 最后判断该结点相邻方格是否为终点，如果不是，则重复第（4）、第（5）步，如果是，则结束估价函数运算排序程序，根据之前每个经过结点周围已存在的父节点，反向标记，找到终点并输出最终优化路径，最后结束全部程序。

1.3 “曼哈顿距离”和“欧几里得距离”

A 星算法的估价函数h(x,y)表示当前结点到目标结点的估计距离（即估计代价），主要可以由“曼哈顿距离”与“欧几里得距离”表示，h(x,y)也分别对应着曼哈顿启发函数与欧几里得启发函数，因此得到最终目标路径的结果取决于h(x,y)所使用的启发函数。

由文献[3]和文献[4]得知，本算法使用的有曼哈顿算法和欧几里得算法。

曼哈顿启发函数为：

式中：D 表示一个栅格的曼哈顿距离；c 表示当前结点；goal 表示目标结点。

欧几里得启发函数为：

式中：c 代表当前结点；goal 代表目标结点。

因为欧几里得距离接近两点最短距离，所以得到的路径为最短距离，同时结合曼哈顿启发算法，可以保证路径的稳定性，计算后得到最优途径路线。

“曼哈顿距离”取决于考察结点与起始结点、终止结点的正交型距离（如图3 所示），在网格图中操作处理和运算较为方便，但是要求单位网格边长远小于目标路径长度以减小误差；而“欧几里得距离”则直接量取起点和终点间的直线距离，即为两点间最短距离（如图4 所示），误差小、准确性高，但是对程序汇编的要求较高，运算相对复杂。

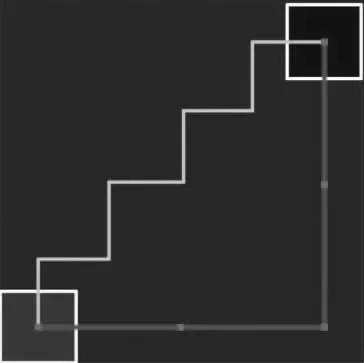
图3 曼哈顿距离

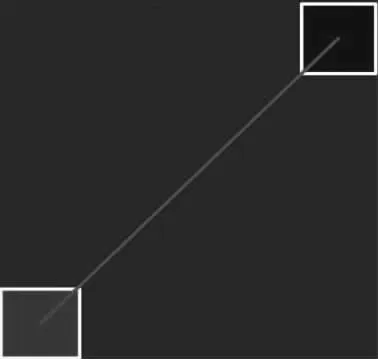
图4 欧几里得距离

我们目前在对充电桩优化布局的研究中主要使用的是“曼哈顿启发函数”，今后可能根据“欧几里得启发函数”对“A 星算法”进行改良，进而解决实际生活中更为复杂的布局问题。

2 使用A 星算法解决电动充电桩优化布局问题

2.1 构建网格图

为实现A 星算法进行布局的优化分析，我们团队联系实际，以南京市为整体研究对象，查找了目前清晰度较高的南京市地图，以单个小格为单位元，绘制出网格表，并以图层叠加方式将其覆盖，根据生活经验和实际考察，将电动汽车难以通行的地方（如山、江、湖）作为障碍物，制作出简单的网格图（如图5 所示），之后又将这些障碍物在网格图上标示（如图6 所示），之后借助MATLAB2022a 进行仿真模拟，再根据“A 星算法”的估价函数进行运算，最终求得最优路径。

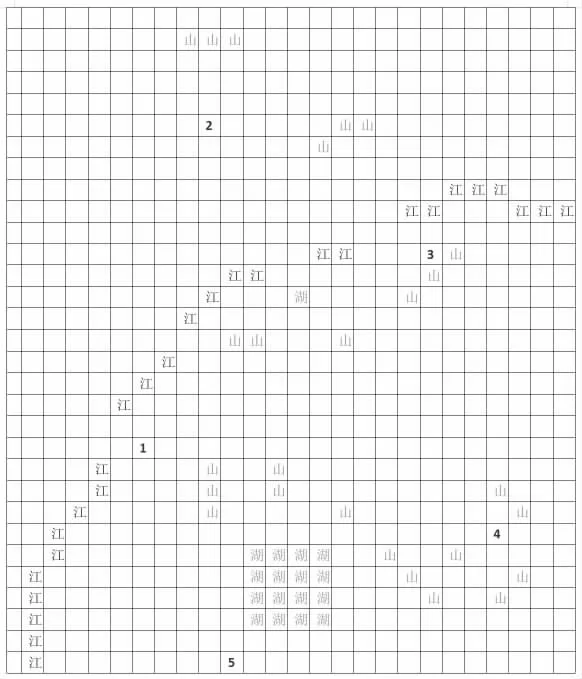
图5 构建实物网格图模型

图6 构建简易网格图模型

我们将以此图为范例，对现有的“A 星算法”计算最优路径启发函数进行改进，实现新能源汽车充电桩的优化布局分析。

2.2 起点和终点的选定

在“A 星算法”最优路径的搜索中，除障碍物以外，还需要有起点和终点位置。我们团队多方查找相关资料，结合实地背景通过线上线下相结合的方式，获得南京市人口密度图与南京市道路交通分布图，寻找南京市边界的人口密度高值区与城际道路发达区域的交集，将该区域抽象化为一个点，作为其中一个起止点，以同样的方法在南京市边界内共找出5 个点（如图5、图6 所示），分别标记为1 到5，在南京市边界上近似均匀分布。

为避免片面性，我们将这5 个点对应的周围极小的区域类比为数学上的“邻域”思想，由文献[5]可知，点集，称为点P0的δ 邻域。例如，在平面上，如图7 所示。

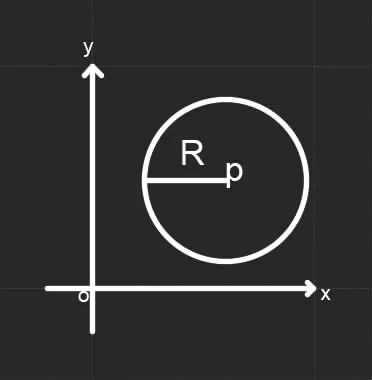
图7 结点及其邻域模型

2.3 联系A 星算法进行的充电桩布局分析

在运用A 星算法解决问题的具体实施步骤如下：

（1） 在一定区域内选取5 个结点（及其邻域）为初始结点和目标结点。

（2） 根据实际区域的障碍物在网格对应位置设置障碍物。

（3） 根据A 星算法的“曼哈顿启发函数”寻找出最短路径。

（4） 再重复以上步骤找出其他路径，得到其交点。

我们将对这5 个点（及其邻域）分别作为该算法“曼哈顿距离”的起止点，我们先创建“OPEN 集合”和“CLOSE 集合”两个列表，分别用于存放网格图中未被处理的结点与已被处理的结点，我们将结点（区域）1定为“START 结点”，根据1.2 中的“A 星算法”的相关流程进行运算，再用MATLAB2022a 对其进行仿真模拟，单一路径仿真结果如图8 所示。

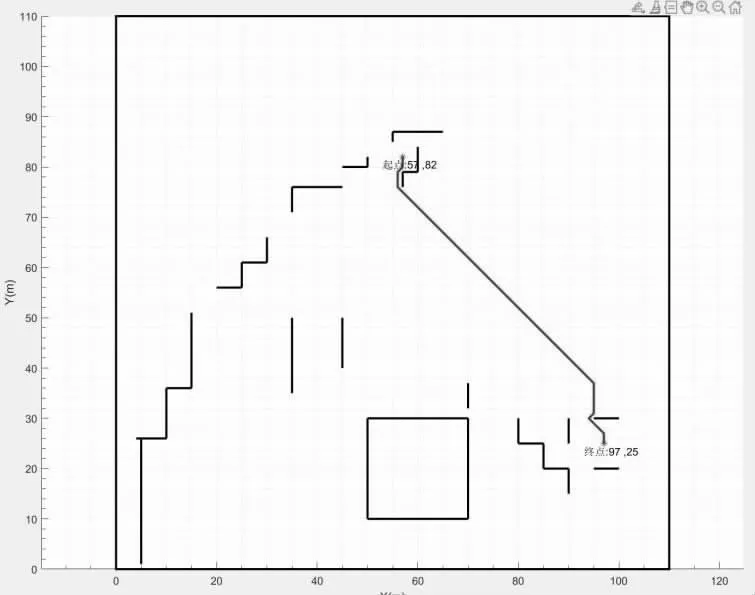
图8 使用MATLAB2022a 得到的单一路径仿真结果

根据图8，我们以中间结点（57,81）为例，介绍A星算法的运算流程，搜索完该结点周围的8 个父结点后，判断出其正下方、右下方两个父节点为“不可用结点”，将其余父结点入曼哈顿距离式中。

我们可以以当前考察结点作为临时原点，将其周围的父节点用二维数组（i，j）表示，其中i、j 可取-1、0、1；在此处，二维数组（i，j）不可取（1，-1）、（0，-1），并且在同一图表中D 为定值，取，代入得

得到6 个估价函数值，将其进行逐一比较，确定其中的最小值，即实现启发式函数的搜索功能，同时也是对该函数功能的检验。经验证，我们可以得到，即f6是最小估价函数值，即（-1，-1）将作为下一次“A 星算法”的“START 结点”进行下一轮运算，最终完成所有相关结点的遍历，得到最优搜索路径。该路径规划方式完全符合原先预期，并更新最优路径的点集。

我们团队基于A 星算法在最优路径规划方面的现有成果，结合南京市障碍的网格图，通过修改A 星算法内的相关参数，在多个非相邻点之间寻找最优路径，将1 到5 这5 个结点（及其邻域）按照搜索单一路径的方法进行相应运算，最终结果如图9 所示。

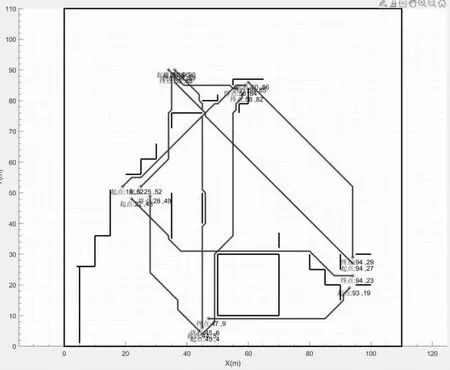
图9 使用MATLAB2022a 得到的单一路径仿真最终结果

根据图9，我们将人口密集及交通发达地区划为“外围区域”，将路径交点周围区域划为“内部区域”（如图10 所示），即锁定图线分布较密集的“内部区域”作为适合安置快充电桩的实际地点。后期我们将进行实地考察观测，在图线相对密集的部分区域内寻找适合建造充电桩的地点，已达成优化布局的最终目的。

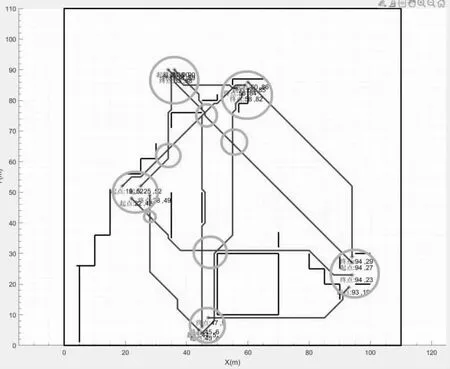
图10 锁定MATLAB2022a 仿真结果中符合要求的区域

【注：图9、图10 中的数据分别为：第一区域：“起点（24，90）”“终点（26，88）”“起点（33，90）”“终点（33，88）”；第二区域：“起点（60，86）”“起点（59，85）”“终点（56，84）”“终点（58，82）”；第三区域：“起点（（19，52）”“起 点（25，52）”“终 点（22，48）”“终 点（28，49）”；第四区域：“终点（94，29）”“起点（94，27）”“终点（94，23）”“起点（93，19）”；第五区域：“终点（47，9）”“终点（45，6）”“起点（44，5）”“起点（45，4）”。（五个区域自左至右、自上向下排序）】

结束语

本文利用“A 星算法”现有的应用形式，将对电动汽车最优路径分析推广到充电桩布局规划，旨在解决现实中充电桩时空分布不均匀等实际问题，并为“A星算法”后续的改良以及其他方面的应用提供了思路，具有一定的创新性和应用价值。发挥现有“A 星算法”的优势，结合一系列改良“A 星算法”，进一步提高了该算法的实用性。我们在MATLAB2022a 中，将城市道路及障碍模型网格化，对优化路径进行一系列仿真实验，先根据路径交点得到一个优化布局位置，再依此进行推广，最终解决布局问题。

然而，本算法在解决此问题中无法同时考虑复杂因素的影响，在后续的研究中，我们将继续细化该模型，紧密结合现有城市背景，充分考虑更多现实因素，如有必要还可能与遗传算法、模拟退火算法等其他经典算法（根据参考文献[6]、文献[7]）相结合对现有算法进行优化改进，进一步完善这一思路，使这一改良分析方案成为今后城市建设方案中的参考之一。