基于孤立森林的城轨车辆空转滑行异常检测方法研究

陈美霞，梁师嵩，胡佳乔

（中车南京浦镇车辆有限公司，南京 210031）

在城轨列车运行中，列车牵引力通过轮轨滚动接触界面上的黏着与蠕滑来传递，轮轨间的黏着—蠕滑特性直接影响列车牵引和制动性能。车轮在原地转动没有前进的现象称为空转，而车轮在钢轨上只有滑动没有滚动的现象则称为滑行［1］。空转会导致轮轨擦伤，而严重的擦伤往往是钢轨疲劳失效的重要原因之一。滑行会形成车轮擦伤，车轮擦伤不仅会使列车运行时车辆/轨道产生强烈振动，还会导致车轮轴承、车轴和轨道的损伤，影响行车安全，增加维修费用；此外，车轮踏面擦伤还会造成轮轨黏着性能进一步降低。

目前城轨列车均已采取一系列的措施应对空转滑行问题，比如喷沙、降低牵引力、制动压力修正等方法［2-8］，虽有一定的效果，但空转滑行现象始终难以完全避免，特别是位于进出站区段站台区域，车辆启停、轨面污染等都会导致空转/滑行问题更加突出。

轻微的空转/滑行现象对于列车运行没有太大影响和安全隐患，经过常规的日常检修即可处理，但较为严重的空转/滑行现象可能需要及时识别出来并对其进行紧急处理。较为严重的空转/滑行现象在列车运行中即可视为异常，文中的目的就是识别出此类异常。因为空转/滑行和列车速度、负载、驾驶模式、路段等息息相关，不适合使用单一的标准进行判断。所以文中针对该问题，提出了一种基于孤立森林的异常检测方法。通过对空转/滑行的次数进行监测、统计、分析，并对之建模，进而判断列车或轨道是否存在潜在风险。空转/滑行是列车轴速变化的体现，当列车在低黏着条件下制动或牵引运行时，系统将检测到空转或者滑行，如短时间内次数异常，则可推测黏着条件较差或者速度传感器故障，存在擦轮、冒进、抱死或牵引变流器故障风险。

1 孤立森林算法介绍

孤立森林（Isolation Forest）算法因其具有易于理解、开销小、时间复杂度低等特点，所以采用孤立森林来实现空转/滑行的异常检测。孤立森林算法的步骤如下［9-11］：

（1）首先要获取原始数据集，集中的数据都具有共同的多维特征。

（2）设置样本集大小n和孤立树的数量m。构建一棵孤立树需要从原始数据集抽样出n个数据，作为这棵孤立树的样本数据集。

（3）在样本数据集中，随机选择数据的一个特征，并算出样本集的数据在此特征上的所有值范围，在这个范围中随机选一个值，根据这个特征值对样本集进行划分，将样本中特征值小于该值的数据划分到节点的左子节点，特征值大于该值的数据划分到节点的右子节点。

（4）分别在左右2 个子节点的数据集上重复第3 步的过程，不断随机选择特征进行划分，直到子节点上只有1 个节点无法再分或者节点达到了树的最大深度。

（5）构建好孤立树后，需要计算每个数据在孤立树上的路径长度。计算方法以遍历二叉搜索树的方式从孤立树中搜索每个数据，在孤立树中根据节点的分支条件不断向下搜索，每向下一次则路径长度加1。最后找到数据点后，返回路径长度记为h（x）。

（6）计算待测数据在孤立森林中的平均路径长度，然后带入公式计算出异常指数，计算公式为式（1）～式（3）：

式中：E（h（x））为数据x在所有树中的路程长度均值；c（n）为n个点构建的二叉搜索树的平均路径长度；ξ为欧拉常数；S（x，n）中x为数据编号，n为样本集大小，S为数据x在由n个数据的样本集构成的孤立树中的异常指数。S（x，n）的值与E（h（x））相关，E（h（x））越小，说明数据越早被孤立出来，则S值越大，表示该数据异常程度越高，反之S值越小则异常程度越低。S的取值范围为［0，1］，在正常情况下，数据集中正常数据的异常指数都会在0.5 左右。

2 异常检测方案设计

2.1 总体方案

首先通过数据探索性分析，了解已知数据，探索变量间的相互关系，以此确定与上述背景技术中提出的问题密切相关的参数；然后针对这一系列参数进行数据预处理，完成模型特征构建；接着将构建好的特征参数输入模型，进行模型构建调参；最后将实时数据经过预处理后持续输入已构建好的模型，开始在线运行，以此实现列车当前空转和滑行次数的异常检测。总体方案如图1所示。

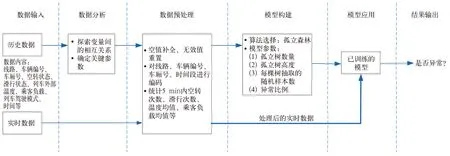
图1 总体方案

2.2 数据探索分析

模型相关的特征数据一般分为类别特征数据和数字特征数据，对于类别特征数据，可做以下分析：类别特征箱形图可视化、类别特征的小提琴图可视化、类别特征的柱形图可视化类别、特征类别频数可视化等。

对于数字特征数据，可做以下分析：相关性分析、特征值分布偏度和峰值、数字特征的分布可视化、数字特征相互之间的关系可视化、多变量互相回归关系可视化等。

2.3 数据预处理

数据预处理分3 步：空值、异常值处理，模型特征构造，数据降维。

（1）空值、异常值处理：空值是指某一条数据缺失某些参数数值，如果缺失参数数量不多且影响不大可不处理；如果缺失数据太多，选择删除；如果缺失参数不多且重要，可采用插值补全方法处理，包括采用均值、中位数、众数等补充。异常值是指数据格式错误或者明显超出参数数值合理范围的数据，该部分数据同样可采用删除或者清空后补全的方法进行处理。

（2）模型特征构造：构造统计特征，例如均值、求和、比例、标准差等；构造时间特征，包括相对时间和绝对时间，工作日、双休日、节假日等；构造地理信息特征，包括坐标区域、分布编码等；特征非线性变换，包括取对数log、平方、开平方根等；通过特征组合、特征交叉构造新特征。

（3）数据降维：如果需要，可采用主成分分析（PCA）、独立成分分析（ICA）、线性判别分析（LDA）等方法降维。

文中输入数据空值、异常值较少，主要采取删除和补全的方式进行处理。特征构造如下：

线路（编码）

车辆编号（编码）

时间段（按5 min 进行时间切片，然后编码）

各时间段内牵引检测滑行次数

各时间段内制动检测滑行次数

各时间段内乘客负载均值

各时间段内乘客负载峰值

各时间段内列车速度均值

各时间段内列车速度峰值

各时间段内列车速度峰值/均值

实际的工作中，地质工程投资时非常复杂的，会受到多方面因素影响，上述安全投资模型是在特定条件下建立的，和地质工程实际情况具有一定的差距。但是实际工作中我们能够以这一模型作为借鉴，从而提升投资的科学有效性，降低其风险。比如，地质工程成本中包含有形成本和无形成本，如事故发生后引发的执政危机，因此，政府相关部门会强制性的要求相关企业在左右决策点的右部进行投资，以便于进一步确保工程的安全性。

所用特征数据维度较小，不进行降维处理。

2.4 模型构建

空转/滑行异常检测模型构建流程如图2所示。

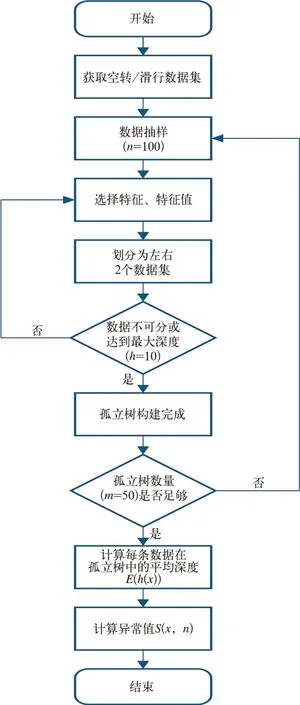
图2 空转/滑行模型构建流程图

文中算法相关参数经过调参之后设置如下：孤立树数量=50，孤立树最大深度=10，每棵树训练样本数量=100，异常比例=0.005。模型构建以及调参完成之后，利用Python 中joblib 软件包保存到本地备用。

2.5 模型应用

模型应用步骤如下：

（1）首先通过Python 中joblib 软件包加载上一步中已构建完成的模型。

（2）接收实时数据，数据预处理。

（3）将处理好的数据输入到已加载的模型。

（4）根据模型输出判断输入数据的异常与否。

（5）将结果反馈至上一层应用系统。

3 实施案例

以下将以南京—宁溧线车辆为例，描述整个方案的实施过程，模型相关参数均可根据不同应用场景和需求进行调整。南京—宁溧线目前有T0～T11 总共12 辆车在线运行，其中针对每一辆车的实施方案均一致，下面以T4 为例进行说明。

3.1 数据探索分析

从空转/滑行产生的基本原理可以推导出与之相关的关键参数主要有车辆载重、驾驶模式、车辆速度、轨面温湿度等，抽取T4 车辆某年7 月11日0 点至7 月12 日0 点的运行数据进行展示，如图3、图4 所示。可以发现，车辆载重、车辆驾驶模式、车辆速度变化情况基本一致，每个站点附近速度会产相应生变化，车辆各轴的载重也会因为乘客上下车发生波动，根据站点ID 变化情况可以看出每跑完一遍线路驾驶模式会有短暂的变化。而空转/滑行发生时间的附近，以上各参数均有相应的变化。

图3 南京宁溧线T4 车运行参数变化情况

图4 南京宁溧线T4 车运行站点停稳信息变化情况

进一步将数据按5 min的时间长度进行切分统计，T4 车 某年7 月11 日10 点～11 点相 关参数 统计信息如图5、图6 所示。可以看出，滑行事件主要发生在10∶00∶00 至10∶05∶00 之间，这个区间发生滑行的车厢转向架载重均值、载重峰值均较大。而该时间段内，在速度峰值较高的情况下，平均速度却很小，说明该区间内存在较大减速操作。综上可知，载重均值、载重峰值、速度均值、速度峰值、速度峰值均值比均与空转/滑行有一定的关联。

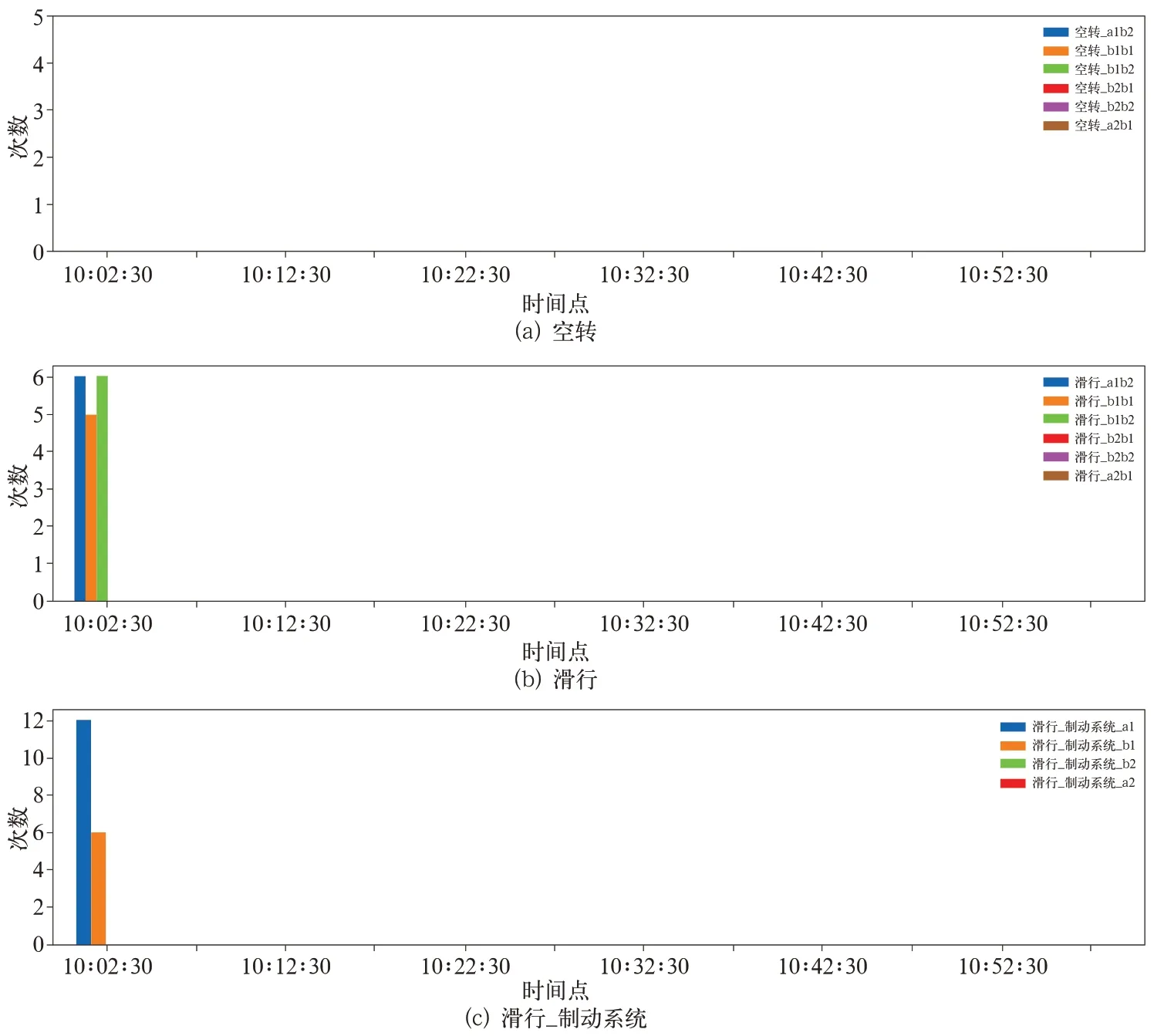
图5 南京宁溧线T4 车空转/滑行统计（7-11 10:00～ 7-11 11:00）

图6 南京宁溧线T4 车载重及速度信息统计（7-11 10:00～ 7-11 11:00）

3.2 数据预处理

在上述数据探索分析过程中发现有部分时间数据缺失，主要采取删除的方式处理，重要数据采取补全措施。

根据数据探索分析结果，主要特征构造如下：

5 min 内A1 车B2 架空转次数

5 min 内B1 车B1 架空转次数

5 min 内B1 车B2 架空转次数

5 min 内B2 车B1 架空转次数

5 min 内B2 车B2 架空转次数

5 min 内A2 车B1 架空转次数

5 min 内牵引检测A1 车B2 架滑行次数

5 min 内牵引检测B1 车B1 架滑行次数

5 min 内牵引检测B1 车B2 架滑行次数

5 min 内牵引检测B2 车B1 架滑行次数

5 min 内牵引检测B2 车B2 架滑行次数

5 min 内牵引检测A2 车B1 架滑行次数

5 min 内制动检测A1 车滑行次数

5 min 内制动检测B1 车滑行次数

5 min 内制动检测B2 车滑行次数

5 min 内制动检测A2 车滑行次数

5 min 内乘客负载均值

5 min 内乘客负载峰值

5 min 内列车速度均值

5 min 内列车速度峰值

5 min 内列车速度峰值/均值

3.3 模型构建

首先通过数据预处理步骤准备好模型训练数据，文中选取南京—宁溧线T4 车某年7 月11 日0点至7 月12 日0 点数据作为训练数据，按5 min的时间长度进行切片，然后按照上一步进行处理，最后获取288 条训练数据。

模型算法孤立森林相关参数经过调参之后设置如下：孤立树数量=50，孤立树最大深度=10，每棵树训练样本数量=100，异常比例=0.005。将训练数据输入模型，开始训练。待模型训练完成之后，利用模型分辨训练数据中的异常数据，得到1条与实际情况一致的异常数据：

［ 0，0，0，0，0，0，6，5，6，0，0，0，12，6，0，0，……］

以上数据对应字段含义依次为：

5 min 内A1 车B2 架空转次数

5 min 内B1 车B1 架空转次数

5 min 内B1 车B2 架空转次数

5 min 内B2 车B1 架空转次数

5 min 内B2 车B2 架空转次数

5 min 内A2 车B1 架空转次数

5 min 内牵引检测A1 车B2 架滑行次数

5 min 内牵引检测B1 车B1 架滑行次数

5 min 内牵引检测B1 车B2 架滑行次数

5 min 内牵引检测B2 车B1 架滑行次数

5 min 内牵引检测B2 车B2 架滑行次数

5 min 内牵引检测A2 车B1 架滑行次数

5 min 内制动检测A1 车滑行次数

5 min 内制动检测B1 车滑行次数

5 min 内制动检测B2 车滑行次数

5 min 内制动检测A2 车滑行次数

模型构建完成之后，利用Python 中joblib 软件包保存为本地文件备用。

3.4 模型应用

首先采用Python 脚本加载上一步骤中保存下来的模型文件，然后将实时数据按照第2 步骤中的方法进行预处理，随后输入模型，通过模型的predict 方法获取模型判断结果，最后将模型结果以及相关数据一同反馈至上一层应用系统。

采用南京宁—溧线T4 车某年7 月12 日0 点至7 月20 日0 点数据模拟实时数据输入模型，得到2条与实际情况一致的异常数据：

［ 0，0，0，3，3，0，0，0，0，0，0，0，0，0，0，0，……］

［12，23，15，16，21，27，0，0，0，0，0，0，0，0，0，0，……］

前6 项分别为：

5 min 内A1 车B2 架空转次数

5 min 内B1 车B1 架空转次数

5 min 内B1 车B2 架空转次数

5 min 内B2 车B1 架空转次数

5 min 内B2 车B2 架空转次数

5 min 内A2 车B1 架空转次数

4 结论

空转/滑行异常难以准确检测的问题，文中提出基于孤立森林的检测方法可以很好地解决。从实施案例可以看出，对于车辆空转/滑行异常的识别达到了预期的效果。后续计划进一步优化算法，收集更多的训练数据（包括正常和异常数据），以达到更加精确的判断结果。