基于Hellinger 距离的正态云相似性度量方法及应用研究

许昌林，徐浩

（1. 北方民族大学 数学与信息科学学院，宁夏 银川 750021; 2. 北方民族大学 宁夏智能信息与大数据处理重点实验室，宁夏 银川 750021）

随着信息技术不断进步，信息过载问题日益突出推荐系统是解决过载问题的一种手段，由Goldberg 等[1]提出的协同过滤推荐系统是应用最广泛的一种，已被阿里巴巴、亚马逊等电商平台广泛应用。云模型作为研究不确定性的一种工具，能有效处理推荐系统中的不确定信息[2-4]，同时云模型在用户识别[5]、多属性决策与优化[6-7]、综合评价[8]等领域也得到广泛应用，其中云概念相似度扮演重要角色。因此，构造合适的相似度不仅能够降低计算复杂度而且能够提升运行效率。如张光卫等[3]将云概念数字特征作为向量构造夹角余弦得到云概念相似性比较方法(likeness comparing method based on cloud model，LICM)，并将其应用于协同过滤推荐。但LICM 将各数字特征赋予相同权重，而数字特征中期望往往大于熵和超熵，导致LICM 区分能力较弱。李海林等[9]利用云概念几何特征提出了基于期望曲线的云模型(expectation based cloud model，ECM)相似度和基于最大边界曲线的云模型(maximum boundary based cloud model，MCM)相似度，区分度较好但当云概念数量增加时，ECM 和MCM 计算复杂度会急剧增加。汪军等[10]将云概念形状相似性和距离相似性结合构建了云概念综合相似度量PDCM(shape and distance based on cloud model)，并将其应用到分类问题中取得了一定效果，而参数拟合和选择会影响精度。此外，有学者从贴近度、概念跃升、散度和多粒度等方面给出云概念相似度[11-14]，取得一定效果。Li 等[15]从区分性、有效性、稳定性和可解释性方面分析了以上相似度方法优缺点。

基于此，本文主要工作：1) 从正态云的特征曲线(如期望曲线、内外包络曲线等)出发，融合正态云的分布特性，利用Hellinger 距离刻画概率分布间相似性的特点，提出了一种基于Hellinger距离的正态云相似性度量方法，该方法兼顾了云概念的数字特征和分布特性，并讨论了所提方法的性质；2)设计了两种正态云相似度算法，即基于Hellinger 距离及期望曲线的正态云相似性度量方法(Hellinger distance based expectation curve of cloud model，HECM)和基于Hellinger 距离及特征曲线的正态云相似性度量方法(Hellinger distance based characteristic curve of cloud model，HCCM)，并将这2 种方法与已有LICM、ECM、MCM 和PDCM 方法从3 个方面进行对比分析。首先进行数值模拟仿真实验，利用云概念差异度指标验证了本文方法具有较好的区分能力和可行性；其次，在时间序列数据集上进行分类实验，结合分类错误率和CPU 时间代价进行对比分析，结果表明本文方法具有较好的分类性能且时间代价较低；最后，将本文方法应用于协同过滤推荐系统，在电影数据集MovieLens 100k 上进行实验分析，采用平均绝对偏差和均方根误差指标进行精度度量，实验结果表明本文方法在用户评分数据极端稀疏的情况下，仍能取得较理想的推荐质量。

1 正态云及现有云概念相似度方法

1.1 正态云及正态云变换

云模型由数字特征描述不确定性概念整体特性。不同概率分布的云构成不同云模型，鉴于正态分布的重要性和钟型隶属函数的普适性[16]，正态云模型及其相关应用得到了广泛研究，相关定义如下。

定义1[2,17]设U是一个用精确数值表示的定量论域，C是论域U上的定性概念，若定量值x∈U，且x是定性概念C的一次随机实现，x对C的确定度为μ(x)∈[0,1]是具有稳定倾向的随机数，则x在论域U上的分布称为云，每个x称为一个云滴。

定义2[17]设U是一个用精确数值表示的定量论域，C是U上用数字特征(Ex,En,He)表示的定性概念。若定量值x∈U，且x是定性概念C的一次随机实现，若x满足：x=RN(Ex,|y|)，其中，y=RN(En,He)，且x对C的 确定度满足：

则x在论域U上的分布称为二阶正态云。这里y=RN(En,He)表示以En为期望，以He为标准差的正态随机数。

正态云主要通过正态云变换实现定性概念与定量数值间的相互转换，其中正向正态云变换将表征概念内涵的数字特征C(Ex,En,He)转化为定量数值。根据定义2，二阶正向正态云变换(the 2ndorder forward normal cloud transformation，2nd-FNCT)见算法1。比如用数字特征C(25，3，0.5)表征定性概念“年轻人”的内涵[17]，Ex=25表示对“年轻人”的总体期望年龄，由算法1 可得“年轻人”的云图如图1 所示。

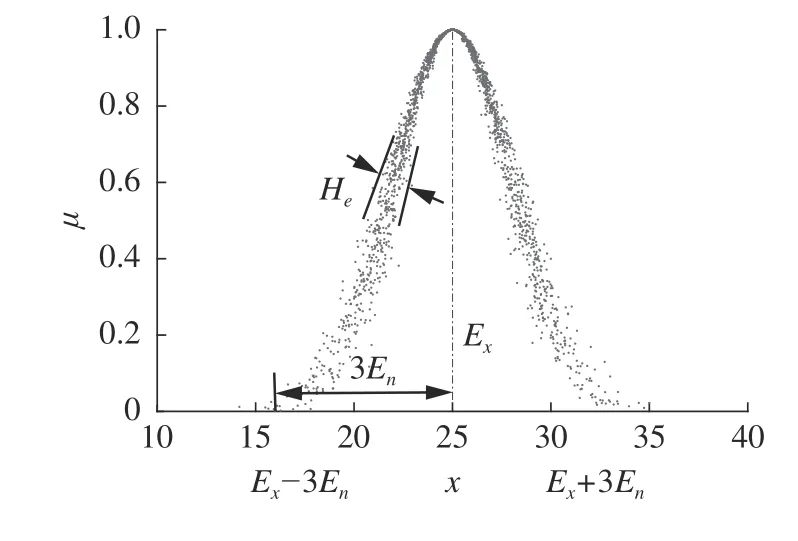
图1 概念“年轻人”C(25, 3, 0.5)的云图Fig. 1 Cloud map of concept “young people” C(25, 3, 0.5)

算法1[17]2nd-FNCT 算法

输入三个数字特征(Ex,En,He)和云滴个数n

输出n样本点(云滴)xi和μ(xi)(i=1,2,···,n)

1) 以En为期望，He为标准差，生成一个正态随机数yi=RN(En,He)；

2) 以Ex为期望， |yi|为标准差，生成一个正态随机数xi=RN(Ex,|yi|)；

4) 具有确定度μ(xi)的xi成为数域中的一个云滴，重复步骤1) ～3)，直至产生要求的n个云滴xi为止。

逆向云变换是将定量数值有效转换为由数字特征C(Ex,En,He)表示的定性概念。目前已有多种逆向云变换算法[17]，本文使用基于样本一阶绝对中心矩和样本方差的逆向云变换算法(single-step backward cloud transformation algorithm based on the first-order absolutely center moment，SBCT-1stM)，如算法2 所示。

算法2[17]SBCT-1stM 算法

输入样本点xi(i=1,2,···,n)

输出反映定性概念数字特征的估计值

1) 根据样本点xi计算样本均值一阶样本绝对中心矩和样本方差S2=

2) 分别计算期望、熵和超熵的估计值：

1.2 二阶正态云的特征曲线

特征曲线能够在一定程度上反映云概念的几何特征。由定义2 和正态分布的“ 3σ”原则知：

当0 ＜He＜En/3时，有99.74% 的云滴确定度μ(x)处于曲线μOut(x) 与μIn(x)之间的区域[17-19]，其中

则称μOut(x)和 μIn(x)分别为二阶正态云的外包络曲线和内包络曲线(如图2)。当超熵He=0 时，云滴确定度聚集分布在曲线上， 称μExp(x)为二阶正态云的期望曲线(如图2)。因此，对定性概念有贡献的云滴99.74%都落在区间[En-3He,En+3He]中，本文正是基于这一特点来构建云概念相似度量。

图2 二阶正态云概念C(25, 3, 0.5)的特征曲线Fig. 2 Characteristic curve of 2nd- order normal cloud concept C (25, 3, 0.5)

1.3 现有正态云概念相似度算法

根据前文所述，下面对已有正态云概念相似度算法LICM、ECM、MCM 和PDCM 进行简要介绍。

算法3[3]LICM 算法

输入数字特征和

输出相似度SLICM(C1,C2)

1) 令U1=(Ex1,En1,He1),U2=(Ex2,En2,He2)

2) 计算C1,C2之间的相似度：He2)

算法4[9]ECM 算法

输入数字特征C1(Ex1,En1,He1)和C2(Ex2,En2,

输出相似度SECM(C1,C2)

1) 若Ex1≤Ex2且初始设置S=0，计算两云概念期望曲线μExp(x1)与μExp(x2)的交点与，设

否则执行4)；

算法5[9]MCM 算法

输入数字特征C1(Ex1,En1,He1)和C2(Ex2,En2,He2)

输出相似度SMCM(C1,C2)

1) 若Ex1≤Ex2且初始设置S=0，计算两云概念外包络曲线μOut(x1)与μOut(x2)的交点与，设令

否则，执行4)。

算法6[10]PDCM 算法

输入数字特征C1(Ex1,En1,He1)和C2(Ex2,En2,He2)

输出相似度SPDCM(C1,C2)

1) 根据熵En和超熵He，计算形状相似度：

3) 将查找到的拟合参数a、b、c代入距离相似度：

4) 计算综合相似度：

上述算法中，由于LICM 算法直接由数字特征通过夹角余弦计算相似度，所以复杂度较低且在协同过滤实验中有一定的效果，但大多数情况下，由于数字特征的期望值或绝对值远大于熵和超熵，此时对数字特征仍采用相同权重，会导致该方法区分能力较弱，后续实验仿真也得到了验证。在ECM 和MCM 算法中，当云概念数量增加时，期望曲线和外包络曲线交叠区域较复杂，从而使这两种算法时间复杂度较高。在PDCM 算法中，与θ近似正态分布关系，对参数θ、a、b、c进行拟合，选取合适拟合参数值计算距离相似度虽然参数拟合选取方法降低了时间复杂度，但参数近似选取以及参数与距离相似度的拟合过程会导致计算误差增大，从而使PDCM算法精度不够高。

2 基于Hellinger 距离的正态云相似性度量方法

针对现有云概念相似度计算方法不足，基于正态云特征曲线从整体上表征正态云概念的分布和Hellinger 距离刻画概率分布间相似程度的特点[20]，本文构造了正态云相似性度量方法。

2.1 两正态分布间的Hellinger 距离

Hellinger 距离是两个统计样本或总体之间重叠量的度量，在概率统计理论中，Hellinger 距离常被用于度量两个概率分布的相似度。具体来说，连续型随机变量概率分布P和Q的Hellinger 距离[20]定义为

其中，p(x)、q(x)分别为分布P、Q的概率密度函数典型。情况下，P表示数据真实分布，Q表示数据理论分布、模型分布或P的近似分布。DH(P,Q)越大表示两分布差异性越大。根据式(5)易得如下结论。

定理1设则P和Q的Hellinger 距离为

由定理1 知，对任意两正态分布，其Hellinger距离都可转为由期望与方差的代数运算，无需进行积分运算，这一特点会将大大降低计算复杂度，而且进一步可得到满足如下性质。

性质1设则

3) 若P和Q同分布于正态分布，即当且仅当

证明1) 由距离对称性知

化简得：

从而有μ1=μ2,σ1=σ2。

2.2 两正态云概念间的Hellinger 距离与相似度

由文献[21]知，二阶正态云概率密度不存在解析解，故直接利用概率密度无法得到DH(P,Q)的解析式。而正态云还可由特征曲线刻画其整体分布，并且将特征曲线按其不确定性特征(熵、超熵) 进行缩放时不会改变原云概念几何性质，故本文间接采用正态云特征曲线计算DH(P,Q)。首先将特征曲线μExp(x) 、μIn(x)与 μOut(x)分别乘相应系数正态化，得到对应特征曲线的密度函数，分别为

根据定理1，由式(8)～(10)，容易得到基于期望曲线μExp(x)、内包络曲线μIn(x)和外包络曲线μOut(x)的Hellinger 距离。

定理2设U是用精确数值表示的定量论域，C1(Ex1,En1,He1)和C2(Ex2,En2,He2)是U上的两个二阶正态云概念，则基于期望曲线、内包络曲线和外包络曲线的Hellinger 距离分别为

根据距离和相似度转换关系，由此得到两二阶正态云概念的相似度度量如下。

定理3设U是用精确数值表示的定量论域，C1(Ex1,En1,He1)和C2(Ex2,En2,He2)是U上的两个二阶正态云概念，那么基于期望曲线、内包络曲线和外包络曲线的相似度分别为

性质2设C1(Ex1,En1,He1)和C2(Ex2,En2,He2)是论域U上的两个二阶正态云概念，则

证明由定义5 和性质1 容易得证(略)。

2.3 基于Hellinger 距离和特征曲线的相似度算法

根据具体应用领域，由期望曲线、内/外包络曲线的不同组合，通过加权求和形式计算其相似度，这种方法体现了云概念整体的分布特性。基于此，设计了两种相似度算法，分别见算法7 和算法8。

算法7HECM 算法

输入数字特征C1(Ex1,En1,He1)和C2(Ex2,En2,He2)

输出相似度SHECM(C1,C2)

2) 计算相似度SHECM(C1,C2)=1-DEHxp(C1,C2)。

算法8HCCM 算法

输入数字特征C1(Ex1,En1,He1)和C2(Ex2,En2,He2)

输出相似度SHCCM(C1,C2)

2) 计算相似度SHCCM(C1,C2)=1-DHCCM(C1,C2)。

3 实验对比分析

为说明算法HECM 和HCCM 有效性和可行性，1) 通过数值仿真实验验证HECM 和HCCM算法的可行性；2) 在UCI 数据库时间序列数据集上检验算法的分类性能和计算时间代价；3) 将算法应用于协同过滤推荐系统中，并在电影数据集上进行实验对比分析。开发工具为Python3.8，运行环境为Windows 10-64 位操作系统，CPU 为AMD Ryzen 54600U with Radeon Graphics 2.10 GHz，16 GB 内存。

3.1 数值仿真实验

本文在文献[3,9-10]给出的4 个正态云概念上进行数值仿真实验，并将所提出的HECM 和HCCM 算法与算法LICM[3]、ECM[9]、MCM[9]和PDCM[10]进行比较，其中正态云概念分别为:C1(1.5，0.626 66，0.339)，C2(4.6，0.601 59，0.308 62)，C3(4.4，0.751 99，0.276 76)和C4(1.6，0.601 59，0.308 62)，对应云图如图3 所示，不同算法计算结果如表1 所示。

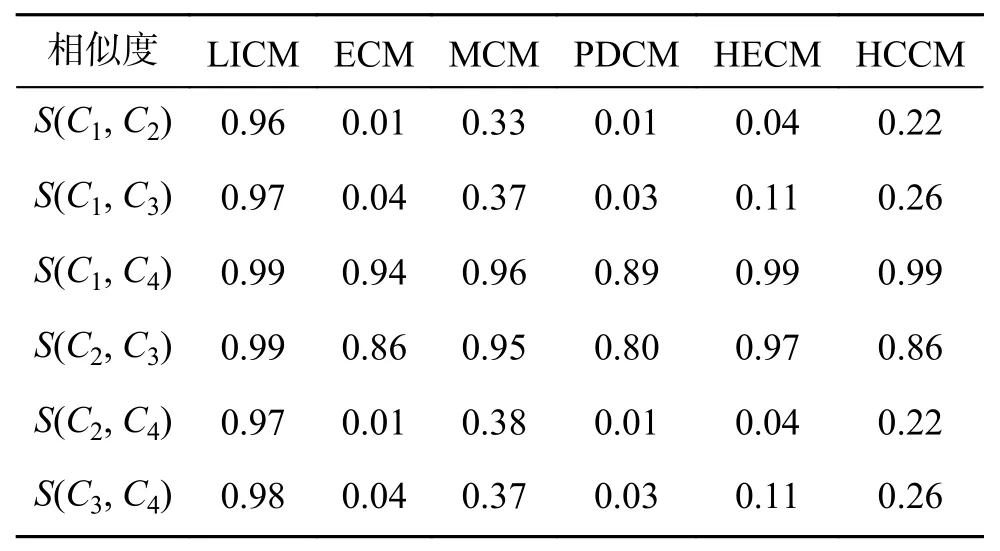
表1 不同相似度算法下云概念Ci(i=1,2,3,4)的相似度Table 1 Cloud concept Ci(i=1,2,3,4)similarity under different similarity algorithms

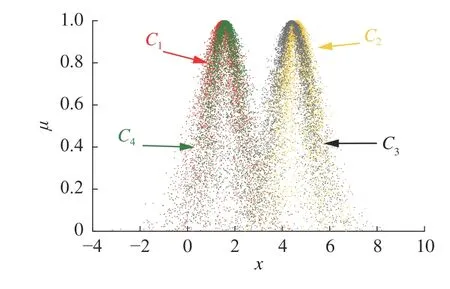
图3 二阶正态云概念C1、C2、C3、C4云图Fig. 3 Cloud map of 2nd- order normal cloud conceptC1,C2,C3,C4

由表1 看出，HECM、HCCM 与ECM、MCM和PDCM 算法都得到C1与C4最相似，C2与C3最相似，S(C1，C4)和S(C2，C3)远大于其他任意两概念的相似度，且S(C1，C4)＞S(C2，C3)，而LICM 得到的这4 个云概念间的相似度都较接近，均在0.95 以上。若将这4 个云概念进行二分类，那么可以认为概念C1、C4属于同一类，概念C2、C3属于同一类。

为比较各方法区分能力，借鉴文献[12]云概念差异度思想，即对某个云概念来说，若与它属同类的云概念相似度越大，而与它属不同类的云概念相似度越小，说明该度量方法能有效区分不同类的云概念云概念，Ci差异度定义为

其中：Cj代表与Ci属同类的云概念，Ck代表与Ci属不同类的云概念。例如云概念C1的差异度为

根据式(14)，各云概念在不同相似度算法下的差异度如表2。由表2 可看出，HECM 算法得到的概念差异度均高于其他算法，这说明HECM算法的区分能力较强，而LICM 算法得到的概念差异度都最小，相似度区分能力最差。与HECM算法一样，ECM 算法得到概念差异度均高于LICM、MCM、PDCM、HCCM 算法得到的概念差异度，说明基于期望曲线得到的概念相似度对这4 个云概念区分能力较强，但期望曲线中没有体现He的作用。在同时考虑数字特征Ex、En、He的相似度算法中，PDCM 和HCCM 得到的概念差异度均高于MCM 和LICM 算法得到的概念差异度。若从计算复杂角度分析，HECM 与HCCM 算法只需进行代数运算，计算复杂度远小于ECM、MCM 以及PDCM。所以综合对比看，HECM 和HCCM 具有较好地性能，在度量云概念相似度方面具有可行性，且计算复杂度较低。

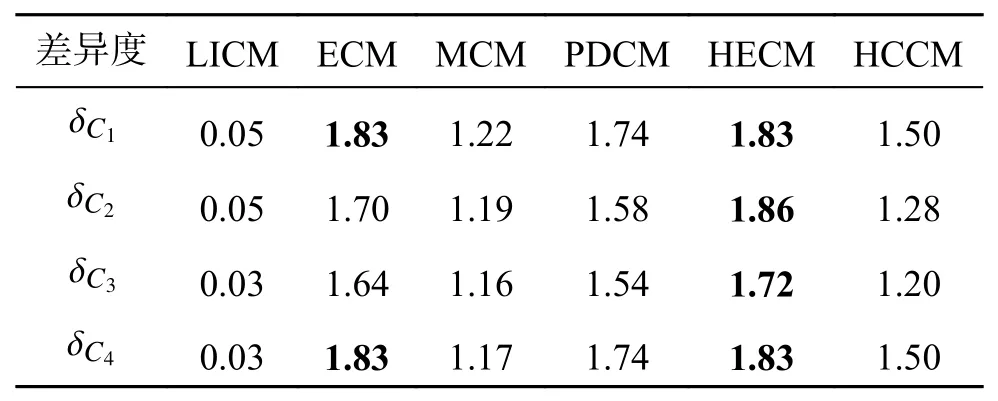
表2 不同相似度算法下云概念Ci(i=1,2,3,4)的差异度δCiTable2CloudconceptCi(i=1,2,3,4)differencedegree δCiunder different similarity algorithms

3.2 时间序列数据分类

时间序列数据由于其高维性，能够较好检验分类算法的性能，采用UCI 数据库中时间序列数据集(synthetic control chart time series)[22]，该数据集分6 类(共600 行60 列)，每行数据代表一个时间序列，每100 行为一类(如表3)，其中Timei代表600 条时间序列数据，Numj代表60 个维度。实验选取每类后10 行为测试集，前90 行为训练集。为提高分类效率，将每个时间序列降维分段处理，训练集和测试集降维后的维数分别为2、3、4、5、6、10、12、20 维。具体时间序列数据分类过程见算法9。

表3 时间序列数据集Dm×nTable 3 Time series dataset Dm×n

算法9时间序列数据分类算法

输入时间序列数据集Dm×n

输出分类错误率和计算相似度CPU 时间代价

1) 划分数据集。取每类数据前90 行作为训练集， 每类数据的后10 行为测试集，即训练集为540 个时间序列数据，测试集为60 个时间序列数据，并将时间序列数据集分段降维处理， 降维后维数分别为2、3、4、5、6、10、12、20 维， 即分割后数据的分段数为2、3、4、5、6、10、12、20 段。

2) 对分割后的每一段数据按照类别进行逆向云变换，得到相应云概念数字特征。

3) 在同一维数段上云概念，分别利用LICM、ECM、MCM、PDCM、HECM 和HCCM 算法计算每一类训练集云概念与其他类测试集云概念的相似度，得到相似度矩阵。

4) 根据最近邻思想，在每一维度矩阵下取相似度最大的类作为分类结果(例如2 维时，共2×6=12 类；3 维时，共3×6=18 类，依此类推)，并根据分类结果计算分类错误率和计算相似度CPU时间代价。

由算法9，LICM、ECM、MCM、PDCM、HECM和HCCM 算法在不同维数下分类错误率、分类错误率平均值和标准差分别如图4 和表4 所示，同时各算法相似度计算CPU 时间代价如图5 所示。

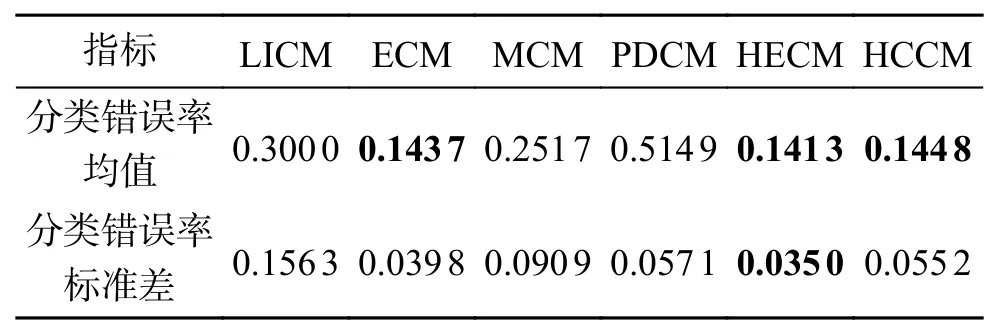
表4 不同维数下不同算法的分类错误率均值和标准差Table 4 Mean value and standard deviation of classification error rate of different algorithms under different dimensions

图4 各算法时间序列数据分类错误率Fig. 4 Classification error rate for time series data of each algorithm

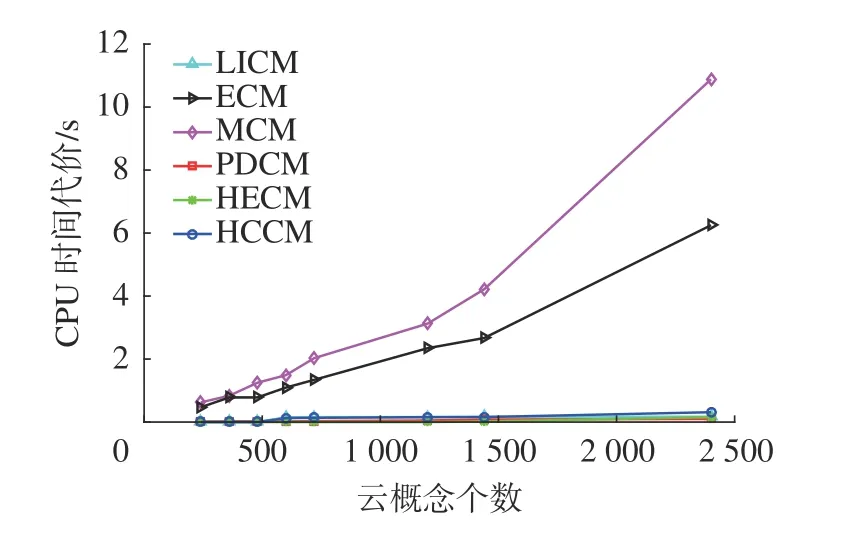
图5 各算法相似度计算CPU 时间代价Fig. 5 CPU time cost of each algorithm to calculate similarity

由图4 可知，维数为2、3、4、5 维时，各算法的分类错误率均有波动。根据表4 分类错误率标准差，LICM 算法稳定性较差，其他几种算法的分类错误率较稳定。从分类错误率来看，PDCM 算法在不同维数下分类错误率都较高，LICM 算法随维数增加分类错误率呈现增加趋势，ECM、HECM和HCCM 算法相比其他几种算法分类错误率都较低，且HECM 算法平均分类错误率和标准差都最小，说明HECM 算法分类性能和稳定性更好。此外，除ECM 和HECM 算法外，HCCM 与LICM、MCM 和PDCM 算法相比有更低的错分率和稳定性。尽管ECM 和MCM 算法的分类错误率整体低于LICM 和PDCM 算法，但由图5 知，ECM 与MCM 算法的时间复杂度远高于HECM与HCCM 算法，且随云概念个数增加，ECM 与MCM 算法CPU 时间代价呈现增大趋势。因此，综合看，HECM 和HCCM 算法在时间序列数据集上都具有较好的分类性能。

3.3 不同算法在协同过滤推荐中的应用

3.3.1 协同过滤推荐算法描述

协同过滤(collaborative filtering，CF)推荐假设相似用户可能喜欢相似项目，通过分析用户的历史行为数据对目标用户行为进行预测并进行有效推荐，详细步骤见算法10。

算法10协同过滤推荐算法

输入用户评分表

输出目标用户UID 对项目IID 的推荐评分

1) 计算用户-项目矩阵Rm×n。根据用户评分详情，列出用户-项目评分矩阵Rm×n，共m行用户，n列项目，则第i行第j列元素rij表示第i个用户对j个项目的评分，即

2) 计算用户评分频度向量。根据1)中用户项目矩阵Rm×n，统计出每个用户的评分频度向量Ui=[u1u2···uG](1 ≤i≤m)，其中ug(g=1,2,···,G)代表用户i对每个项目评分为g的频数，G为项目评分最高分值。

3) 计算用户评分特征向量。根据用户评分频度向量Ui，将用户的每一次评分视为云滴，通过逆向云变换算法计算得到每个用户的评分特征向量Vi=[Exi Eni Hei],(1 ≤i≤m)。

4) 计算用户相似度矩阵。用户相似度矩阵表示为

其中，S(i,l)表示用户i与l的相似度(1 ≤i,l≤m)，分别由LICM、ECM、MCM、PDCM、HECM 和HCCM 算法计算。

5) 形成推荐。根据目标用户UID、用户相似矩阵Sm×m和用户-项目矩阵Rm×n，在用户空间中查找对该项目有评价记录且与目标用户最接近的k个最相似邻居用户，得到最近邻居集Neih=其中，Neih1与目标用户相似度最高，Neih2与目标用户相似度次之，依次类推。根据最近邻集合Neih形成推荐，预测目标用户UID对待推荐项目IID 的评分PUID→IID。本文采用加权平均策略得到预测评分PUID→IID[4]，计算方法如下：

式中：rui→IID为用户ui对待推荐项目IID 的评分，S(UID,ui)为目标用户UID 对近邻用户ui的相似度。

3.3.2 协同过滤推荐算法在影评数据集上的比较

MovieLens100k 数据集[23]是收集用户对电影评分信息，并通过历史打分信息将预测评分较高的电影推荐给目标用户。数据集从1997 年9 月19 日至1998 年4 月22 日收集943 个用户对1 682部电影的评分记录，共100 000 条，该数据集用户评分数据稀疏等级为1-(100 000/9 431 682)=0.937。将数据集以80%和20%比例划分训练集和测试集，推荐质量评价指标采用平均绝对偏差(mean absolute error，MAE)和均方根误差(root mean squared error，RMSE)。

其中：预测用户评分为pi，实际用户评分为qi。一般情况下，MAE 与RMSE 越小推荐质量越高。文献[3]已说明LICM 算法推荐效果优于余弦相似性、修正余弦相似性和BP-CF(back propagationcollaborative filtering)方法，故此次实验只将HECM和HCCM 算法与LICM、ECM、MCM 和PDCM 算法的推荐效果进行对比。其中最近邻居数k分别取10、20、30、40、50、60，各算法在k不断增加时推荐效果的MAE 和RMSE 变化分别见图6 和图7，不同算法在k取不同值时的MAE 和RMSE 平均值如表5 所示。

表5 不同算法在最近邻居个数k 取不同值时对应的MAE均值和RMSE 均值Table 5 MAE mean and RMSE mean corresponding to different algorithms when the nearest neighbor k takes different values

图6 最近邻居个数k 增加时各算法的MAE 取值Fig. 6 MAE value of each algorithm when the nearest neighbor number k increases

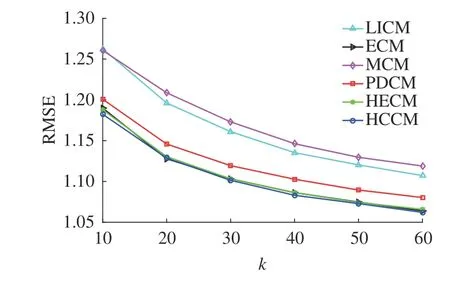
图7 最近邻居个数k 增加时各算法的RMSE 取值Fig. 7 RMSE value of each algorithm when the nearest neighbor number k increases

从图6 和图7 看出，随着k从10 增加至60，6 种相似度算法的MAE 和RMSE 均呈现下降趋势。结合表5 可看出，LICM、MCM 和PDCM 算法相比ECM、HECM 和HCCM 算法得到的MAE 和RMSE 都较高，推荐质量相对较差。相比之下，E C M、H E C M 和H C C M 算法得到的MAE 和RMSE 在6 种算法中比较小且取值接近，且HCCM 算法得到MAE 和RMSE 是最小的，拥有更准确的推荐效果，推荐质量最优，说明HCCM 算法拥有一定的优越性。

根据上述实验结果，本文方法与其他方法相比有如下优势: 1) 从计算角度和效果看，同时考虑云概念3 个数字特征，且通过3 条特征曲线研究正态云相似性，综合考虑了云概念的几何特性，并综合量化云概念间的差异，考虑了更多的信息，信息损失少，所以概念区分度和分类性能都较好；2) 从计算过程看，利用数字特征只进行简单的代数运算而无需进行较为复杂的积分运算，与ECM、MCM、PDCM 算法相较而言更为简单，所以具有较低的计算复杂度；3) 从推广角度看，由于Hellinger 距离是一种f 散度且满足距离公理化定义，所以由此得到的云概念相似度具有较好的性质，容易推广至高阶正态云和高维云模型中，具有普遍适用性。

4 结束语

本文主要针对现有正态云相似性方法存在问题，结合正态云特征曲线几何特性和Hellinger 距离刻画概率分布相似性特点，提出了基于Hellinger距离的正态云相似性度量方法，并构造了2 种正态云概念相似度计算算法。通过数值仿真、时间序列数据分类实验，将本文方法与已有方法进行对比，最后将本文方法应用于协同过滤推荐，实验结果均表明本文方法拥有良好性能和推荐质量。基于Hellinger 距离和正态云特征曲线构造的云概念相似度为云概念相似度的测量提供了一种新思路，容易将其推广至高阶正态云和高维云模型中。与此同时，结合领域问题，如何选择合适的特征曲线构造相应的Hellinger 距离，将是下一步需要进行研究的主要工作。