结合深度乐谱特征融合的钢琴指法生成方法

李锵，吴正彪，关欣

（天津大学 微电子学院, 天津 300072）

钢琴指法（piano fingering）是影响钢琴演奏效果的重要因素，也是钢琴演奏初学者遇到的学习难题。然而，大量的乐谱缺乏指法注释，给演奏者带来了巨大困扰。利用计算技术为乐谱自动标注指法，可以拓宽初学者选择乐谱的范围，去除演奏的首要障碍，拓展钢琴演奏人群，保护钢琴练习的兴趣。

自动钢琴指法作为音乐信息检索[1]领域的子任务，很早便受到研究者们的关注。较早的自动指法生成方法基于规则，使用主观定义的指法转移规则来建立代价函数，以代价函数值最小为目标求解指法路径。Parncutt 等[2]将长程指法生成任务视为动态规划问题并建立12 条指法转移规则，根据规则建立求解动态规划问题的代价函数。Balliauw 等[3]扩展Parncutt 的研究，将指法生成视为一个组合优化问题，设计可生成指法的变邻域搜索算法。Al 等[4]定义相邻音符与和弦音符的水平损失和垂直损失，以此寻找指法的传输路径。这些基于规则的方法易于理解，但模型需要手动设置参数，且人工定义的规则不适用于所有演奏情况。

因为基于规则的方法存在设置模型参数困难、规则完备性欠缺的问题，基于数据驱动的方法成为近年来自动指法生成研究的热点。基于数据驱动方法将钢琴指法生成看作自然语言处理领域[5]的序列标注[6-7]问题，使用传统统计学习模型或者深度学习模型学习音高和指法间的映射关系。

Yonebayashi 等[8]建立一阶隐马尔可夫模型（hidden Markov model，HMM），使用维特比算法搜索可能性最大的输出指法序列，该方法成功生成单音乐谱的指法。Nakamura 等[9]提出用两个并行的HMM 模型组合输出指法的方法，针对乐谱的高声部与低声部，分别训练两个HMM 模型再合并输出指法，完成双手指法的生成。

随着深度学习技术的发展，有良好时序建模能力的长短时记忆网络（long short-term memory，LSTM）在各类时序处理任务[10-12]中取得了超越传统统计学习模型的性能。于润羽等[13]使用基于LSTM 模型提取文本向量的上下文信息，并结合条件随机场 (conditional random field, CRF) 进行命名实体识别；王一成等[14]使用BiLSTM（bidirectional LSTM）模型，提取文本序列的高阶特征；Siami-Namini 等[15]比较LSTM 和BiLSTM 在预测金融时间序列中的性能；Wang 等[16]设计基于LSTM 的两个模型处理音频序列的梅尔倒谱系数，提升语音情感识别的准确性；Liu 等[17]使用BiLSTM 结合注意力机制提取文本序列的局部特征。

因为LSTM 优秀的序列处理性能，使得LSTM模型成为近年来指法生成任务中的主流模型。Nakamura 等[18]研究深度神经网络在指法生成中的应用，使用前馈网络和LSTM 生成指法。Ramoneda等[19]设计基于LSTM 和图神经网络的两个自回归模型进行微调，提升模型生成和弦指法的能力。Guan 等[20]采用基于RNN 和LSTM 的方法，并提出一个定性评价度量来评估所生成的指法的可弹性。

现有工作仍存在一些问题。现有方法使用音高表示音乐序列，不能表示同样影响指法的速度特征。并且上述研究所用的乐谱数据集规模有限，导致对音乐特征的捕获能力变弱；最后，在训练模型时，上述方法选择对左手指法和右手指法分别训练的方案，分别训练的策略让一个独立模型可用的训练数据变得更少，性能也因此降低。

为应对上述挑战，本文提出融合乐谱综合特征与上下文信息的指法生成系统。首先，设计一种乐谱综合特征提取方法，同时提取乐谱的音高信息与速度信息并生成原始乐谱特征向量；其次，针对乐谱特征向量之间的时序性，引入Word2Vec-CBOW 模型，用自监督学习的方法提取原始乐谱特征向量的上下文信息、融合乐谱特征向量；同时，根据左右手镜像对称的特性，提出左右手互相转化的数据增强方法，增加单个模型可用的数据量；最后，结合BiLSTM-CRF 模型，实现钢琴指法的自动生成。

1 自动指法生成系统

本文算法的结构如图1 所示。该系统由4 部分组成：乐谱特征提取层、数据增强模块、Word2Vec-CBOW 特征融合层和BiLSTM-CRF 指法生成层。乐谱特征提取层进行数据预处理，获取综合性的乐谱特征向量；数据增强模块实现序列的转换，使得模型可以同时训练左手数据与右手数据；Word2Vec-CBOW 特征融合层利用乐谱上下文信息训练原始乐谱特征向量，获得融合特征向量E(t)；BiLSTM-CRF 指法生成模块用于捕获融合特征向量与输出指法序列之间的映射关系，并学习输出序列内部的约束。

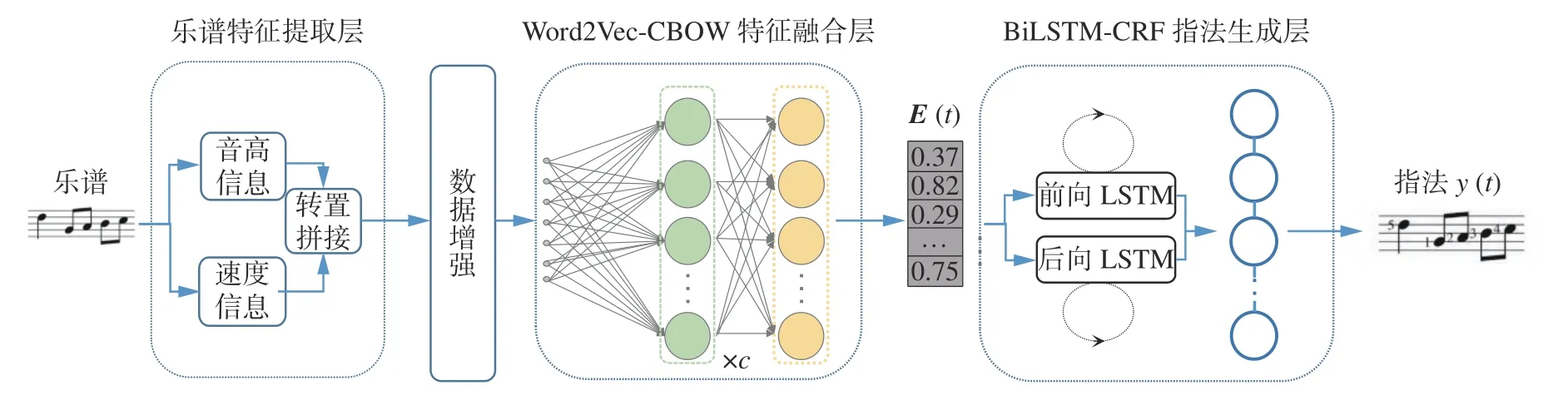
图1 指法生成系统Fig. 1 Fingering generation system

1.1 乐谱特征提取层

在实际弹奏时，速度同样影响指法[21-22]。基于此，设计可以同时提取音高信息和速度信息的乐谱特征提取方法，如图2 所示。

图2 乐谱特征提取层Fig. 2 Musical score feature extration layer

乐谱特征提取层基于音高序列P、音符开始时间ton和结束时间toff，对原始乐谱进行数据预处理。

音高信息反映手指在演奏时的位置。提取音高的独热向量p，音高差分编码d、黑键标识符与和弦标识符作为音高相关特征。音高独热向量p即为音高MIDI 的独热编码。音高差分编码[19]d的基本思想是用相邻的音高作差，以此表示琴键的相对距离，其计算方法为

式中：d(t)为当前时间步的音高差分编码，x代表的是音高MIDI，t为时间步长变量，k表示和弦中包含的音符数，若为单音，k规定为0。

黑键标识符或者和弦标识符为布尔值。设置为1 时，说明当前音高对应的琴键是黑键或者当前音是和弦。当手指按压于黑键或者演奏和弦时，一些特定的指法是不可用的[19]。

另一方面，音乐的速度信息影响弹奏时指法的疲劳感和舒适度[2]。定义音符的稠密度和真实时值作为速度相关特征。稠密度定义为当前音符开始后，1 s 内会响起的音符个数。真实时值的定义为音符结束时间toff和开始时间ton的差值。

在经过图2 的乐谱特征提取层之后，音符序列将从单个音高量作表述的一元码元序列，扩展为多维特征向量组成的多元码元序列，以便后续的Word2Vec-CBOW 训练。

1.2 数据增强

左手的升调演奏与右手的降调演奏受到的人体工程学约束是相同的[1]。基于这一特点，可将左手的音高差分编码转化为右手的音高差分编码。

考虑左手音高差分编码是非和弦时，左手的升调演奏与右手的降调演奏的d(t)是相同的，故得到

式中：dR(t)是右手音高差分编码，dL(t)是左手音高差分编码。

考虑当前音符是和弦时，根据式（1）和式（2），得到

式中：xL为左手的原始音高数据，k为和弦指法所用的手指数。

结合式（2）与式（3），可以得到基于左右手对称特性的数据转换方法：

式中：dR(t)是dL(t)通过式（2）转化而来的右手音高差分数据，k表示和弦中包含的音符数。

完成式（4）的转化之后，左手音高差序列dL(t)替换为新的dR(t)，其余特征不变。训练时左手数据与右手数据共享参数，实现左右手联合训练。

1.3 Word2Vec-CBOW 特征融合层

Word2Vec-CBOW[23-28]的滑窗全连接层机制，可提取当前时间步的上下文训练融合特征向量，这一特点适合对多维乐谱特征建模。

Word2Vec-CBOW 模型的结构如图3 所示。图中x(t)表示原始特征向量，E(t)为训练完成的融合特征向量。Word2Vec-CBOW 是自监督模型，使用原始数据训练融合特征向量而不需要指法标签。图3 中的c为窗长参数，代表该模型利用当前时间步t周边的前c-1和后c-1个原始乐谱特征向量来训练融合特征向量。

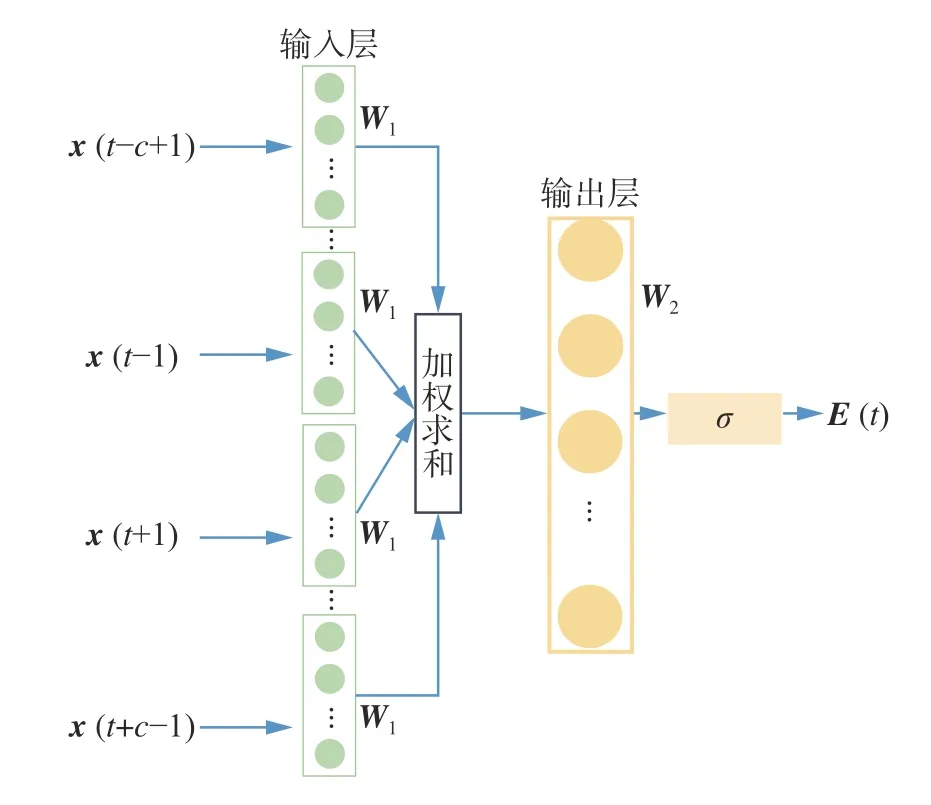
图3 Word2Vec-CBOW 特征融合层Fig. 3 Word2Vec-CBOW feature fusion layer

图3 输入层前将t时刻周边2（c-1）个原始特征向量向量进行线性变换，以此提取当前时间步的上下文信息，这一过程表示如下：

式中：Yin是输入层的输出向量，W1∈Rv×n是输入层的训练权重矩阵，v为原始特征向量维度，n为输入层神经元个数，窗长内的每一个原始乐谱特征向量共享相同的训练权重矩阵W1。

输出层使用全连接层增加融合特征向量的拟合能力，其公式为

式中：W2∈Rn×v是输出层的权重矩阵,σ 是Sigmoid激活函数，E(t)是训练好的维度为v的融合特征向量。

最后，Word2Vec-CBOW 模型的训练目标为

式中x(t)是原始特征向量。该训练目标使融合特征向量不丢失原始的乐谱特征。

训练时，使用随机梯度下降法训练模型，损失函数选择交叉熵函数，通过反向传播算法更新权重矩阵W1和W2。

1.4 BiLSTM-CRF 指法生成层

输入的乐谱序列是一段连续的多维时间序列，需要综合前后时间的信息对当前乐谱状态作出判决。并且输出指法之间存在一定的转移限制，这就需要算法学习输出指法之间转移概率。因此本文使用结合BiLSTM 与CRF 层的指法生成方法。BiLSTM 对输入的乐谱特征序列进行双向递归处理，可以更好地学习双向时序关系。CRF模型对BiLSTM 生成的指法序列进行约束学习，得到更加合理的指法结果。

图4 是BiLSTM-CRF 在时间维度上的示意图。E(t)的是前述的融合特征向量， At与 A′t为LSTM 的基本单元，其具体结构可参考文献[26-28]。

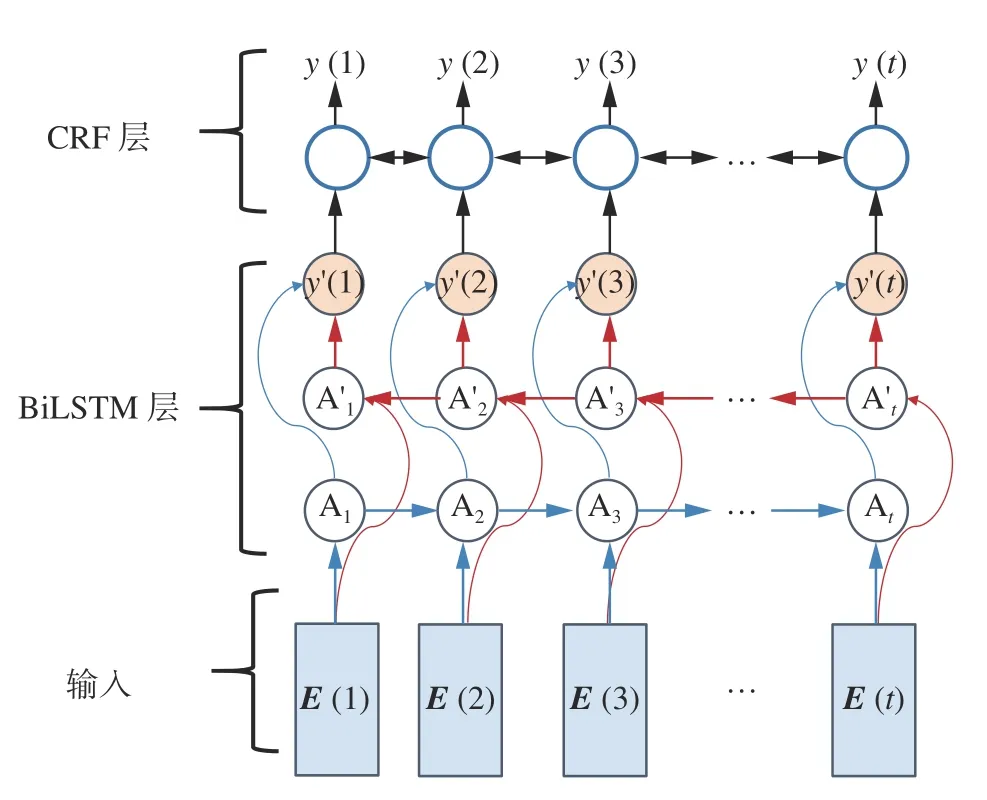
图4 BiLSTM-CRF 指法生成层Fig. 4 BiLSTM-CRF fingering generation layer

BiLSTM-CRF 指法生成层对条件概率P(Y|E)进行建模，其中Y=[y(1)y(2) ···y(t)]T是待预测的指法序列，而E′=[E(1)E(2) ···E(t)]T是Word2-Vec-CBOW 输出的多维时间序列。训练时采用极大似然估计原理，使P(Y|E′)最大化。该条件概率可表示为

损失函数使用负对数似然函数，其表达式为

2 实验与分析

2.1 实验环境与参数设置

本实验环境如下：操作系统为Windows 10，内存为64 GB DDR4 3 600 MHz，CPU 为Intel i9-9900X，GPU 为4 x Nvidia RTX2080Ti（11 GB），使用Pytorch 作为深度学习框架。

本文使用七折交叉验证方法进行实验。Word2-Vec-CBOW 的窗长设置为2，初始学习率为0.004，使用Adam 优化器调整权重。实验时Word2Vec-CBOW 和BiLSTM-CRF 分开训练，Word2Vec-CBOW 的损失函数为交叉熵函数，BiLSTM-CRF的损失函数为负对数似然函数。每次交叉验证均训练10 轮（epoch）。模型参数如表1。

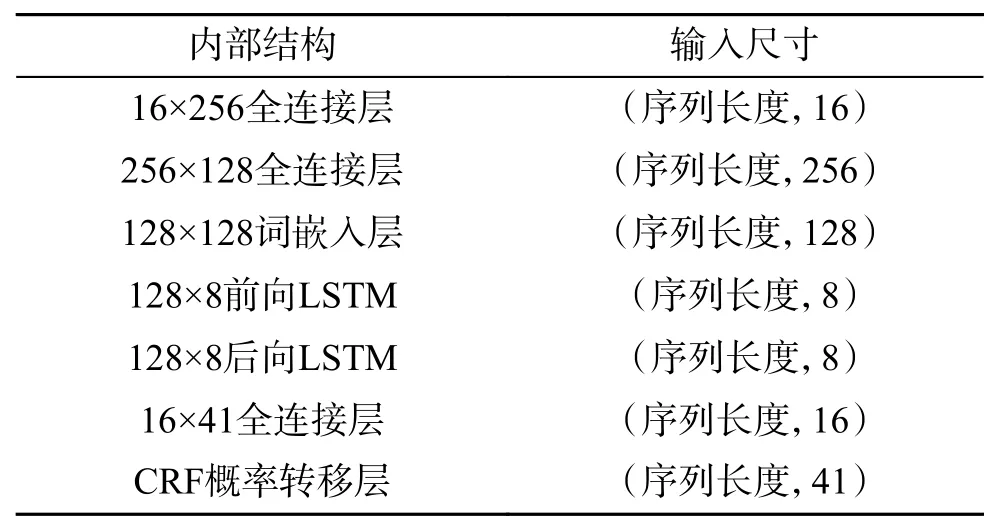
表1 模型参数Table 1 Model parameters

2.2 数据集

实验使用的数据集是Nakamura 等[18]在2019年发布的PIG 数据集和自建数据集。PIG 数据集是一个标注好指法的公开乐谱数据集，包含有150首乐谱，共有309 首指法标签数据。自建数据集中包括巴赫的28 首乐谱，车尔尼的20 首乐谱和中国音乐学院社会艺术水平考级1～3 级中节选的7 首乐谱，共计55 首乐谱数据。两数据集共364 首乐谱数据、145 129 个音符数据。

2.3 评价指标

在数据集中有许多首乐曲存在多个指法标签数据。计算实验结果和所有真实标签的匹配率ai,j，取其平均值Mgen作为评价指标，其计算方法为

式中：N是测试集乐曲总数，ai,j表示指法估计结果与第i个乐谱的第j个指法标签真值序列的匹配率。对于特定的i和j，ai,j的计算方法为

式中：n为该乐曲的序列长度，y是模型生成的指法，是真实指法标签，XNOR代表同或计算。

对于数据集中多标签的乐谱数据，使用另一个评价指标，最高匹配率Mhigh，Mhigh的表达式如下：

需要注意的是，钢琴的正确指法不是唯一的，每一段乐谱对应的指法可能有很多种。使用匹配率指标只能在一定程度上体现模型标注指法与标签的相似性。

2.4 实验结果与分析

2.4.1 消融分析

为验证本文系统中引入的各部分模型的有效性，笔者开展消融实验。消融实验的结果如表2所示。

表2 消融实验结果Table 2 Results of ablation experiment%

实验B 的模型在仅使用音高输入的情况下，Mgen下降2.66%，Mhigh下降3.02%，这说明本文设计的乐谱特征提取层在钢琴指法生成任务中起着重要作用。

实验C 的模型将左右手弹奏的乐谱序列用两个模型分别训练，而非合并在同一个模型中训练。在左右手音符数据分别训练的情况下，模型的Mgen下降2.84%，Mhigh下降1.90%，验证了本文提出的数据增强在指法生成任务中的有效性。

实验D 的模型直接将特征提取层输出的原始乐谱特征向量作为源数据。实验结果表明，在未使用Word2Vec-CBOW 的情况下，模型的Mgen下降3.81%，Mhigh下降3.81%。这意味上下文信息特征向量建模可以提高生成指法的准确性。

2.4.2 与其他算法的对比

为比较本文算法与常见指法生成算法的有效性，笔者将本文算法与前馈网络[18]、LSTM[18]与BiLSTM[20]做对比，如表3 所示。其中，文献[18]是首个使用深度学习网络进行指法生成的研究，而文献[20]算法对乐谱的黑白键信息建模，与本文算法思路较为相似。此外为体现出本文算法的先进性，笔者还选取了综合性能较好的AR-LSTM(autoregressive-LSTM)[19]与AR-GNN (autoregressive-graph neural network)[19]做比较。

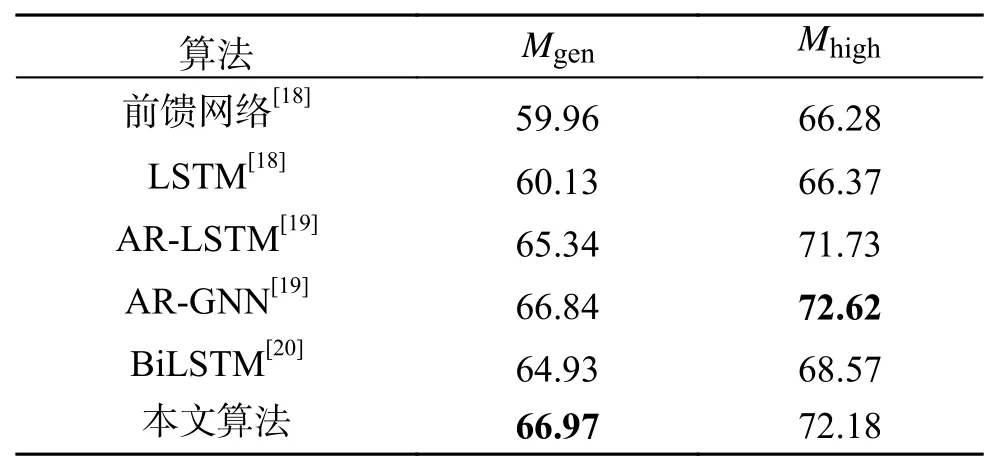
表3 不同算法的结果对比Table 3 Results of different algorithms%

将本文算法与文献[18]提出的前馈网络以及LSTM 进行对比，本文算法在两个指标上均有着很大的优势。

与文献[19]提出的AR-LSTM 和AR-GNN 相比，本文算法在Mgen指标上均有优势，而AR-GNN在Mhigh指标上较高。AR-GNN 是使用一个噪声较大的超大音乐数据集预训练后，再在PIG 数据集上微调得来的。其在预训练阶段时使用的数据量上远大于本文算法所使用的数据量。

与文献[20]提出的BiLSTM 相比，本文算法在两个指标上均有优势。这说明本文提出的深度特征融合方法与数据增强方法，具有较强的乐谱特征提取能力。

此外，为比较不同算法在训练时所需的计算量，笔者将不同算法的计算复杂度展示于表4。表4 中，n为输入音符序列的长度，l为神经网络的层数，d为音符嵌入向量维度，h为LSTM 中隐藏层大小，c为Word2Vec-CBOW 的窗长。

表4 不同算法的计算复杂度Table 4 Computational complexity of different algorithms

如表4，前馈网络与AR-GNN 的计算复杂度与n成二次关系，而本文算法的计算复杂度与n成线性关系。当输入音符序列长度较长时，前馈网络与AR-GNN 的计算成本较本文算法高。而与其他基于LSTM 的算法[18-20]相比，本文算法较LSTM[18]以及Bi-LSTM[20]复杂度高，但在性能上超越了这些算法。而与AR-LSTM[19]相比，本文算法在计算复杂度相近的情况下能获得更佳的性能。

2.5 实例分析

本节中，笔者给出了本文算法与前馈网络[18]、BiLSTM[20]在实验结果上的区别，以突显本文算法的优势。

2.5.1 单音乐谱实例

如图5 所示，单音旋律的输出指法是单维的，与真值标签不同的指法已用虚线框标出。图5中，本文算法生成与真值标签一样的指法。而前馈网络生成与真值标签不同的3-5-4 指法。虽然生成的3-5-4 指法是可弹奏的，但相比本文算法生成的指法，该指法需要移动手位，而非仅移动手指，这会带来顿挫感。说明前馈网络对手指位置信息的捕获能力不如本文算法。而在BiLSTM 生成的指法中，出现与真值标签不同的2-1-2 指法。该指法对手指独立性要求高，若演奏者缺乏练习，会加剧疲惫感。这说明仅使用BiLSTM 无法学习指法之间的约束，导致该模型欠缺对连贯性的考虑。而本文算法引入CRF 层，学习到了指法标签间的约束。

图5 单音乐谱指法实例（选自巴赫BWV 827《谐谑曲》）Fig. 5 Example of monophonic fingering (from Bach BWV 827 “Scherzo”)

2.5.2 复音乐谱实例

图6 给出了在复音旋律上生成指法的样例。复音旋律的指法是多维的，对演奏者的技巧要求更高。

图6 复音乐谱指法实例（选自肖邦《英雄》）Fig. 6 Example of polyphonic fingering (from Chopin“Heroes”)

本文算法生成的指法虽与真值标签略微不同，但是生成的指法是可弹奏的。前馈网络生成的指法与真值不匹配、不合理之处较多。BiLSTM 生成的指法虽可弹，但在第3、4 个时间步中，使用25-15 指法。该指法与真值标签24-15 指法相比，对手指独立性有一定的要求，在速度较快的情况下要求演奏者有较高的演奏水平。相比于BiLSTM，本文算法生成的指法在高速情况下更容易演奏。这说明本文提出的乐谱特征提取方法捕获了对指法判决有重要影响的速度信息。

3 结束语

本文提出一种基于深度乐谱特征融合的BiLSTM-CRF 指法生成方法。该方法综合性地提取乐谱的音高信息和速度信息，基于左右手对称的特点实现数据增强，引入Word2Vec-CBOW 模型融合乐谱特征向量，利用BiLSTM-CRF 模型自动生成指法。通过消融实验、横向对比以及实例分析，证明本文提出的算法相较于几种常用的算法性能更好，并且利用了乐谱的速度信息使得生成的指法更具优势。本研究目前仍然有可提高的地方：本文算法并不能完美地生成一些特殊的指法，如同音换指、轮指；此外，LSTM 的自回归特性使得模型会出现误差传播的问题。未来的工作将继续寻找更优的网络结构、更合理的特征提取方法，以及生成指法速度更快的网络结构，以期实现对指法生成模型的进一步优化与改进。