基于误差补偿LSTM-GRU 的综合能源系统多元负荷预测*

耿 阳 王海龙 张 楠 付 明

(1.国网江苏省电力有限公司扬中市供电分公司 扬中 212200；2.国电南瑞科技股份有限公司 南京 211106；3.国网江苏省电力有限公司镇江供电分公司 镇江 212000)

1 引言

随着我国经济、工业的迅速发展，能源短缺问题已经成为制约我国发展的重要因素。综合能源系统考虑多种能源形式之间的耦合关系，提高了能源的利用效率，显著减少了能源的浪费[1-3]。精确的负荷预测是提高经济调度有效性的重要保证，对经济调度、最优潮流、电力市场交易等有着重要的意义。综合能源系统具有多种形式的负荷，多种形式的负荷互相影响，不能只考虑单一能源形式的负荷预测，需要对多元负荷进行联合预测[4-6]。

如今常用统计学方法和机器学习方法来进行负荷预测。传统的数学统计方法有指数平滑法[7]，卡尔曼滤波法[8-9]和多元线性回归法[10]等。这类算法虽然有一定的成效，但对受到多种因素影响的短期负荷预测而言，无法对波动性和随机性强的负荷进行精确预测，结果难以参考。当前大量使用的机器学习的预测方法主要有支持向量机[11-12]、随机森林[13]和神经网络[14-16]等。在训练样本较大的情况下，支持向量机和随机森林等方法存在收敛速度较慢的缺点，而且对数据十分敏感，神经网络的出现很好地解决了上述问题。

近年来，比较前沿的机器学习方法在解决复杂预测问题时，通过多层神经网络之间的映射关系就可以很好地对输入与输出之间的关系进行拟合。长短期记忆(Long short-term memory，LSTM)网络和门控循环单元(Gated recurrent unit，GRU)等依靠其对时间序列的数据较强的处理能力从而得到广泛的应用。文献[17]将LSTM 方法用在超短期负荷预测中，该方法包括使用LSTM 建模进行全天负荷预测与周期滚动预测，再利用相似日数据对周期滚动预测结果进行修正。

单一预测模型预测精度有限，大量的研究结果表明，将多种模型或者算法结合的组合预测模型的预测精度明显优于单一预测模型[18-20]。文献[18]使用卷积神经网络(Convolutional neural network，CNN)与双向长短期记忆(Bi-directional long short-term memory，BiLSTM)网络组合模型进行负荷预测，在预测之前先挖掘数据的时序特征，提高了预测模型的精度。文献[19]利用猫群优化算法(Cat swarm optimization，CSO)寻找反向传播(Back propagation，BP)神经网络的最优参数，进一步优化BP 神经网络的预测精度。当前对于组合预测模型的研究主要着重于利用机器学习进行数据特征挖掘，再进行负荷预测，或者利用一些新颖的算法对神经网络的参数进行优化来寻找最优的神经网络参数，上述方法对负荷预测都有进一步的提升，但是很少有着重于对负荷预测的结果进行误差补偿的研究。

针对上述方法的不足，本文在考虑误差补偿的前提下，提出利用GRU 网络对负荷预测的误差进行补偿，将预测模型和误差补偿模型的结构重构，得到最终的负荷预测结果。仿真结果表明本文提出的负荷预测模型相较于其他模型具有更高的精确度，验证了所提方法的可行性。

2 多元负荷及气象因素相关性分析

综合能源系统中存在大量的能量转换设备，例如电锅炉、电转气(Power to gas，P2G)设备和冷热电联产(Combined cooling heating and power，CCHP)系统等，所以综合能源系统中各种形式的能源之间具有较高的耦合度，需要区别于传统的电力系统负荷预测。对综合能源系统的多元负荷进行联合预测时，应该考虑到各种形式负荷之间的相互耦合关系。

影响综合能源系统负荷预测精度的因素众多，除了考虑各负荷之间的耦合相关性，还需要考虑气候环境等因素。但是并非所有的气象因素都需要考虑，有些因素并不会对负荷预测的结果产生很大的影响，而且会大大增加系统的复杂度。为了针对性地进行影响因素的选择，本文选择灰色关联度分析方法来分析各影响因素与多元负荷之间的相关性，从而选择合适的影响因素进行负荷预测。

2.1 灰色关联度分析

灰色关联度分析(Grey relation analysis，GRA)用来描述不同因素之间随时间或对象变化的关联性的大小。基本思想是通过确定参考数据和若干个比较数据的几何形状相似程度来判断其联系是否紧密，反映了曲线间的关联程度。目前综合能源系统和电力系统的负荷预测大多采用皮尔逊相关系数法对负荷和影响因素进行相关性分析，但电负荷、热负荷、冷负荷和气象因素之间的关系是非线性的，更适合使用GRA 方法。而且GRA 方法不需要以大量的数据为基础，可以减少信息不对称带来的损失。

GRA 方法需要首先确定参考数据和比较数据，并对数据进行无量纲化处理，方便比较。通过式(1)和式(2)分别计算关联系数和关联度。最后，对关联度进行排序，若r1>r2，则对于同一参考数据，x1优于x2。

式中，ξi(k)为关联系数；y(k)为参考数据的第k个值；xi(k)为第i列比较数据的第k个值；ρ为分辨系数，取值为0≤ρ≤ 1，一般取0.5。在本文模型中，y(k)表示电、热、冷负荷等多元负荷，xi(k)表示可能对多元负荷产生影响的各影响因素。

式中，ri为关联度，ri值越接近1，说明当前选取的y(k)与影响因素xi(k)的关联度越高，即影响因素对负荷的影响就越大；n为序列中数据的个数。

2.2 多元负荷预测影响因素选择

利用美国亚利桑那州立大学的能源信息系统和“Campus Metabolism”网站2020 年6—8 月的多元负荷数据以及同时期的温度、湿度、风速、太阳辐射等气象数据，采取上述的GRA 方法对综合能源系统多元负荷与气象因素之间的相关性进行分析，依次求得电负荷、冷负荷和热负荷与各影响因素之间的关联度大小，根据关联度的大小选择合适的影响因素进行多元负荷预测，结果如表1 所示。

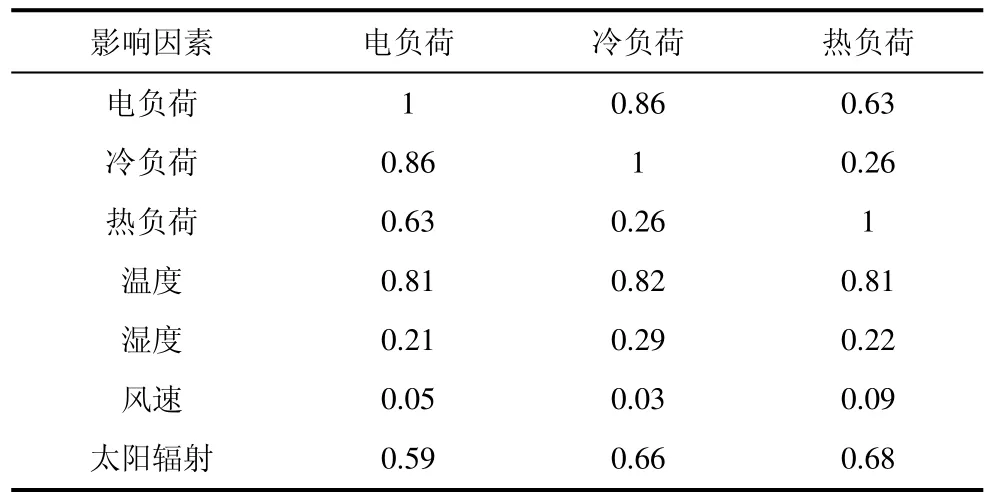
表1 多元负荷与影响因素的关联度

从表1 中可知，电负荷、冷负荷、热负荷和除风速外的各气象因素之间存在很高的相关性。风速与电热冷负荷的相关性均小于0.1，所以在负荷预测中可以不考虑风速对负荷预测结果的影响，进而减小系统的复杂度。电负荷与冷负荷的相关性为0.86，这是因为所选数据为夏季的综合能源系统多元负荷数据，而夏季电负荷多用于空调等设备制冷，因此夏季电负荷与冷负荷的相关性要高于电负荷与热负荷的相关性，符合现实规律。

因此，本文多元负荷预测的主要影响因素有电负荷历史数据、热负荷历史数据、冷负荷历史数据、温度、湿度、太阳辐射和日类型信息，将工作日与休息日分别用1 和2 表示。通过灰色关联度分析方法选择对多元负荷影响较大的因素作为该预测模型的输入集，可以大大增加预测模型的精确度，也可以筛选出对多元负荷预测影响较小的因素，简化模型，提高训练与预测效率。

3 负荷预测与误差补偿模型

3.1 LSTM 神经网络模型

长短期记忆(Long short-term memory，LSTM)神经网络是循环神经网络的一种形式。本文使用长短期记忆神经网络是因为其可以很好地对时间序列历史数据进行训练与预测，对于具有强季节性趋势的历史负荷数据十分合适。

LSTM 神经网络的每个神经元都包含输入门、遗忘门和输出门三种门结构，相较于循环神经网络(Recurrent neural network，RNN)增加了用来储存神经元状态的信息流，通过三个门来控制信息的遗忘和传递，LSTM 的结构如图1 所示。

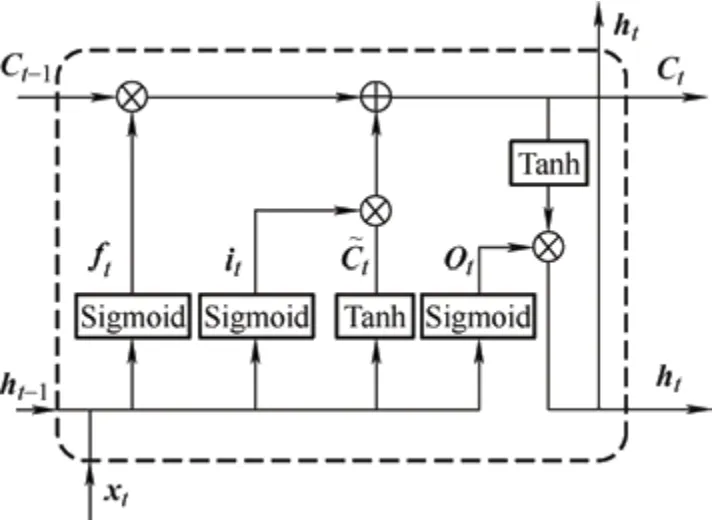
图1 LSTM 神经元结构图

LSTM 模型计算过程为

式中，ft、it、to分别表示神经元的遗忘门、输入门、输出门的输出信号；C~t表示神经元候选状态信息；Ct表示神经元状态信息；th表示神经元的隐状态；tanh()表示双曲正切激活函数；σ表示sigmoid激活函数；Wf、iW、WC、Wo分别表示遗忘门、输入门、记忆单元和输出门的权重；bf、ib、Cb、ob分别表示遗忘门、输入门、记忆单元和输出门的偏置量；xt表示神经元输入序列值；⊙表示逐点乘法运算。

3.2 GRU 神经网络模型

GRU 模型是LSTM 模型的一种改进结构，GRU将LSTM 的门结构进行了合并，可以增加网络的训练速度，并且保证模型的训练精度不会下降。相比于LSTM 的“三门”结构，GRU 只有更新门和重置门两个门结构，对网络结构进行简化，可以提高模型的训练速度。GRU 结构如图2 所示。

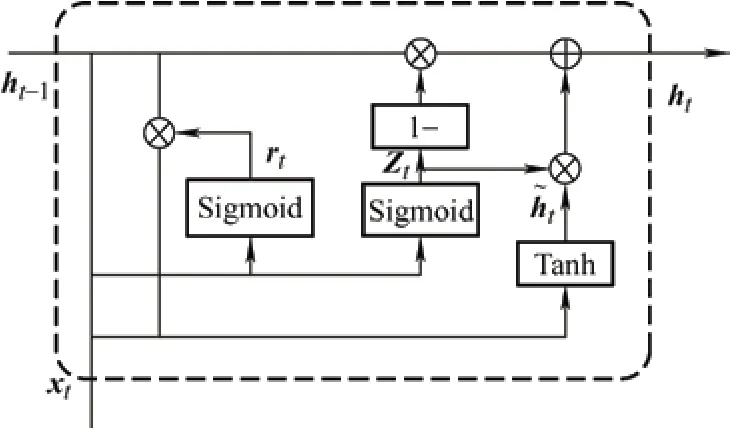
图2 GRU 神经元结构图

GRU 模型计算过程为

式中，tr表示t时刻重置门的输出；Zt表示t时刻更新门的输出；Wr表示重置门的权重矩阵；WZ表示更新门的权重矩阵；Wh~表示候选隐状态的权重矩阵；x t表示GRU 模型在t时刻的输入；th表示GRU模型在t时刻的隐藏层状态输出；t~h表示当前输入的候选隐状态；sigmoid()为S 型激活函数；tanh()表示双曲正切激活函数。

3.3 误差补偿

误差是指测量值偏离真实值的程度，根据误差来源可以分为系统误差、随机误差和毛误差。系统误差由仪器本身误差、采用方法的误差、环境误差等原因导致，理论上可以通过一定的手段或方法来消除；随机误差是由无法控制的变因导致的测量值产生随机分布的误差，它是不可消除的；毛误差主要是因测量者的疏忽而造成，这种误差是可避免的。系统误差对于测量值的影响是通过某种相同的方式，将测量值推向同一个方向，有一定的规律性。

显然，误差与噪声具有明显的差异性，前者有明显的规律性，后者无规律可循。因此可以通过探寻误差产生的规律，对误差进行修正，达到减小误差、提高精度的目的。

负荷预测模型的预测误差不仅包含时间序列预测的随机误差，也包含因模型的性能偏差而导致的系统误差，这种有规律可循的系统误差可通过时间序列预测的误差补偿技术得到适当的补偿和修正，减小误差中的冗余信息，以提高预测精度。

为进一步减小负荷预测模型的预测误差，本文采用误差补偿技术，建立误差补偿模型，对预测误差进行训练学习，进而实现对预测误差的补偿，以提高预测的精度。基于误差补偿的预测方法分如下两步进行：① 利用所构建的预测模型对样本数据进行预测，得到相应的预测误差；② 建立误差补偿模型，将步骤①所得到的误差作为模型的输入，通过模型训练使误差补偿模型的输出逼近样本的误差预测值，将同一个样本的预测值与误差预测值相加，实现对所提预测模型的预测结果的补偿。

4 预测模型

4.1 预测模型结构

本文所提基于误差补偿的综合能源系统多元负荷预测模型的流程如图3 所示，由于LSTM 和GRU网络可以较好地处理时间序列数据，利用LSTM 网络对多元负荷进行初步预测，再使用GRU 网络对预测误差进行补偿，通过将负荷预测值与误差补偿值重构，得到多元负荷预测的最终结果。该模型共有输入层、LSTM 负荷预测层、GRU 误差补偿层、误差重构层和输出层五个结构。

图3 LSTM-GRU 模型流程图

该模型中每一层的详细功能如下所示。

(1) 输入层：负荷数据之间的量纲不同，所以需要对电负荷、热负荷和冷负荷的历史数据进行归一化等预处理，使用归一化数据可以方便模型训练和预测。归一化处理的公式为

式中，X′表示归一化处理后的数据；X表示归一化处理前的数据；Xmax和Xmin分别表示数据序列中的最大值和最小值。

(2) LSTM 负荷预测层：LSTM 层的作用是学习多元负荷历史数据的特征，对多元负荷进行预测。预测结果进行反归一化处理，作为该负荷预测模型的初步预测结果，并求得预测误差作为后续模型的输入。反归一化为归一化的逆运算，其原理为

式中，X表示反归一化处理后的数据；X′表示反归一化处理前的数据；Xmax和Xmin分别表示数据序列中的最大值和最小值。

(3) GRU 误差补偿层：GRU 层的作用是对LSTM 层负荷预测的误差进行学习，并预测出负荷预测的误差补偿值。

(4) 误差重构层：误差重构层的作用是得到最终的多元负荷预测值。将负荷预测层的输出结果与误差补偿层的输出结果做和，得到该多元负荷预测模型的最终结果。

(5) 输出层：将经过误差重构得到的多元负荷预测重构结果作为本模型的预测结果输出。

本文所提多元负荷预测模型的算法流程如图4所示。

图4 多元负荷预测模型流程图

模型的损失函数使用均方误差函数，即

式中，n为样本个数；yi为i时刻的负荷实际值；为模型运算后得到的i时刻负荷预测值。

本文提出的基于误差补偿的综合能源系统多元负荷预测模型结构如图5 所示，首先通过GRA 方法对多元负荷的影响因素进行分析，选取与多元负荷关联度较高的气象因素作为影响因素；影响因素结合历史负荷数据进行归一化处理，处理后的数据进入LSTM 模型进行模型构建和训练负荷预测模型，输出结果为多元负荷初步预测结果；求得LSTM模型的预测误差并进行处理，处理后的数据进入GRU 模型进行模型构建和训练误差补偿模型，输出结果为预测误差应当补偿的值；通过初步预测结果与误差补偿结果的重构，进行反归一化得到多元负荷最终预测结果。

图5 多元负荷预测模型结构图

本文在预测模型的训练过程中，选取Adam 优化算法对模型参数进行优化。Adam 是一种可以替代传统随机梯度下降过程的一阶优化算法，该算法能够基于训练数据迭代更新神经网络的权重，使损失函数输出值达到最优。

4.2 评价指标

为了验证本文所提模型在负荷预测方面的精确性，采用平均绝对误差百分比(Mean absolute percentage error，MAPE)、均方根误差(Root mean square error，RMSE)和平均误差(Mean error，ME)指标对模型的预测准确性进行评估，计算方法为

式中，n表示预测结果数量；yi表示预测值；表示真实值。

评价指标MAPE表示预测值与实际值的偏离程度，表示预测误差与预测结果的百分比；RMSE 和ME 都可以直观表示预测误差的大小，在本算例中RMSE 和ME 的单位都为kW。上述三个指标可以评估模型的预测精度，MAPE、RMSE 和ME 的值越小，代表负荷预测的误差越小，精度越高。

5 算例分析

本文算例利用Matlab 仿真平台搭建了多元负荷预测与误差补偿模型。该算例的数据选取自美国亚利桑那州立大学创建的能源信息系统和“Campus Metabolism”网站2020 年6 月1 日—8 月31 日的多元负荷数据，数据的采样周期是15 min，每天有96个样本数据，数据集共有8 832 个样本。取6 月1日—8 月4 日的数据作为训练集数据用于预测模型的拟合；取8 月5—22 日的数据作为验证集数据用于对模型进行评估；取8 月23—31 日的数据作为测试集数据用于评估模型的预测效果。将8 月30 日与8 月31 日的多元负荷预测误差作为典型的休息日与工作日预测结果进行分析，并将8 月31 日的预测结果进行可视化比较，进一步对本文所提模型的准确性和优越性进行说明。

相较于传统的随机梯度下降法，Adam 优化算法具有更快的收敛速度，计算效率更高，可以代替随机梯度下降法来更新网络权重。网络的最优超参数值通过粒子群算法获得，设定隐藏层神经元个数为200，全连接层神经元个数为50，训练迭代次数为100，初始学习率为0.05，学习率在迭代50 次之后开始衰减，衰减率为0.2，dropout 层的参数为0.5。本文中模型的最大提前预测时间为15 min，属于超短期预测范畴，采用迭代式的预测模式。

5.1 滑动窗口宽度对预测精度的影响

滑动窗口算法是计算机网络中处理数组或字符串问题常用的概念，其基本原理是在数组或字符串中由开始和结束索引定义的一系列元素的集合。滑动窗口顾名思义就是一个可以将两个边界向某一方向“滑动”的窗口，通过窗口框选出数组或字符串中的特定元素集合进行处理。其具体过程如图6所示。

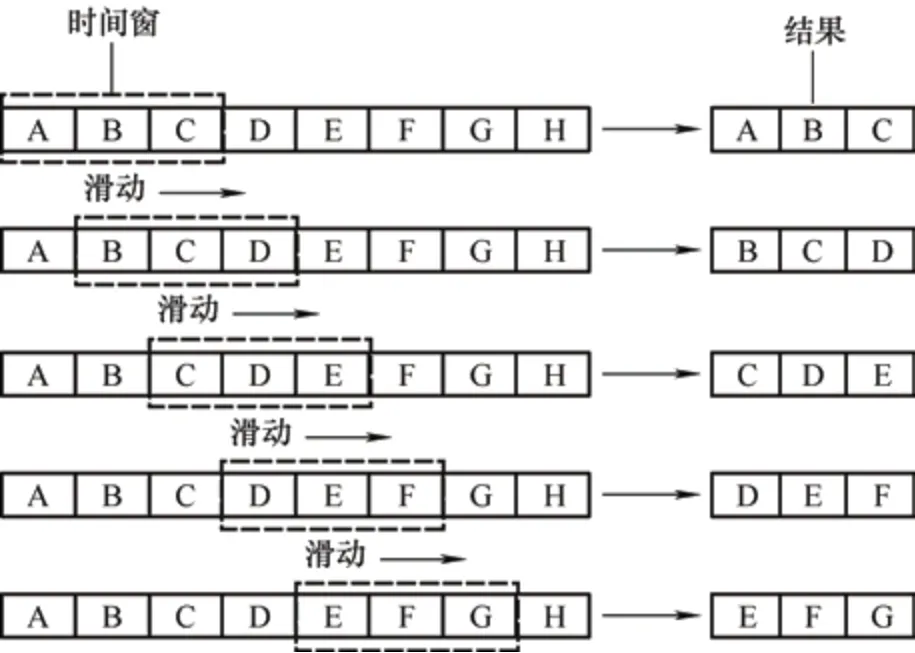
图6 滑动窗口示意图

本文使用基于时间序列的神经网络进行负荷预测，在对负荷数据进行序列化操作时选择使用滑动窗口算法，而滑动窗口的宽度会对预测模型的精确度产生影响，所以需要对不同滑动窗口宽度的试验结果进行对比，选择最合适的滑动窗口宽度。

本文采取的初始滑动窗口宽度为4，每次将滑动窗口宽度扩大两倍，直到滑动窗口宽度为32，之后预测模型的精度会下降，便不再进行研究。使用模型1 表示滑动窗口宽度为4 时的预测模型；模型2 表示滑动窗口宽度为8 时的预测模型；模型3 表示滑动窗口宽度为16 时的预测模型；模型4 表示滑动窗口宽度为32 时的预测模型。不同滑动窗口宽度下的负荷预测模型预测误差如表2 所示。

表2 不同滑动窗口宽度下的预测误差

图7 所示为不同滑动窗口宽度下的电负荷、冷负荷、热负荷预测结果。

图7 不同滑窗宽度下的负荷预测结果

从表2 可知，上述四种模型在不同的日期类型，负荷预测的误差趋势大致相同，主要以工作日为例分析。当滑动窗口的宽度为8 时，该负荷预测模型的预测精度最好。模型1 相比于模型2，电负荷预测结果的MAPE 相等，但是对于冷负荷与热负荷而言，滑动窗口宽度W=8 时的预测精度要优于W=4时的负荷预测精度。W=16 和W=32 时的预测精度明显不如W=8 时的预测精度，所以该预测模型的滑动窗口宽度为8 时，效果最优。因此，本文以下的研究均基于滑动窗口的宽度为8 来展开。

5.2 采样间隔对预测精度的影响

为衡量负荷数据的采样时间间隔对预测模型的影响，本文对不同采样间隔下的负荷数据进行预测，来验证采样间隔对该预测模型预测精度的影响。分别对比采样间隔为15 min、30 min 和60 min 下的预测精度，使用模型5 表示采样间隔为15 min 时的预测模型；模型6 表示采样间隔为30 min 时的预测模型；模型7 表示采样间隔为60 min 时的预测模型。不同采样间隔下的负荷预测模型预测误差如表3所示。

表3 不同采样间隔下的预测误差

图8 所示为不同采样间隔下的电负荷、冷负荷、热负荷预测结果。

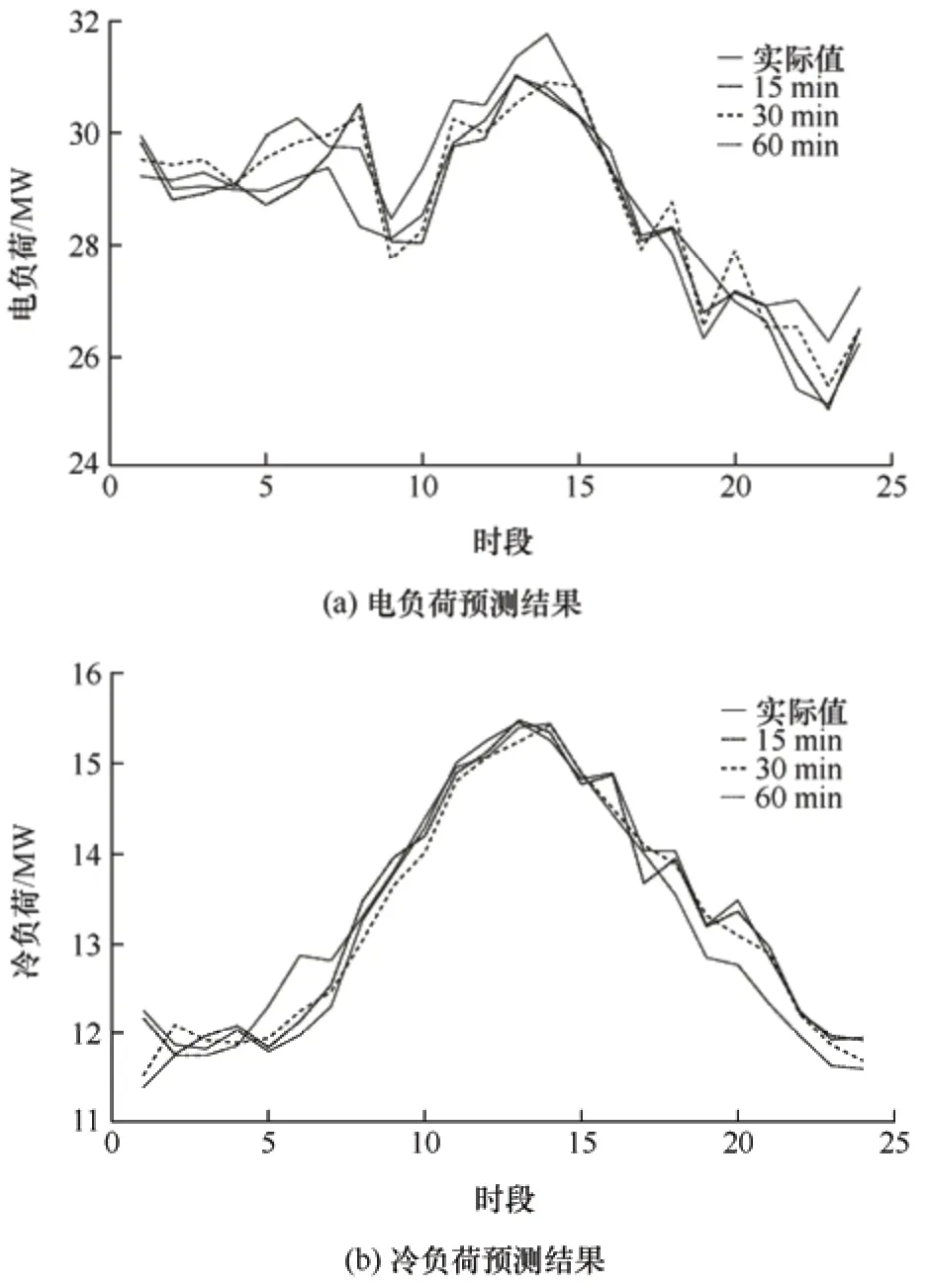
图8 不同采样间隔下的负荷预测结果

从表3 可以看出，在不同的日类型下采样间隔为15 min 时的预测精度均最优。以工作日为例，采样间隔为30 min 和60 min 时预测模型的电负荷预测误差相比15 min 的预测模型电负荷预测的MAPE增加了1.05%和2.01%，RMSE 增加了44.7%和56.6%，ME 增加了52.5%和67.9%；冷负荷预测的MAPE 增加了0.40%和0.72%，RMSE 增加了30.4%和42.4%，ME 增加了32.4%和48.4%；热负荷预测的MAPE 增加了0.52%和1.86%，RMSE 增加了37.9%和66.1%，ME 增加了40.1%和68.1%。从结果可以看出，采样时间间隔对预测模型的精度有很大的影响，而且采样间隔越短，历史数据中所包含的信息就越多，更有利于预测模型对数据中的信息进行提取。因此，本文研究均基于采样间隔为15 min的数据集来展开。

5.3 误差补偿对预测精度的影响

为验证误差补偿在该多元负荷预测模型中对预测结果精度的影响，本文选择在滑动窗口宽度为8，采样间隔为15 min 的前提下，利用历史数据对考虑误差补偿和不考虑误差补偿的多元负荷预测模型的预测效果进行对比，使用模型8 表示不考虑误差补偿时的预测模型，使用模型9 表示考虑误差补偿时的预测模型，预测误差结果如表4所示。

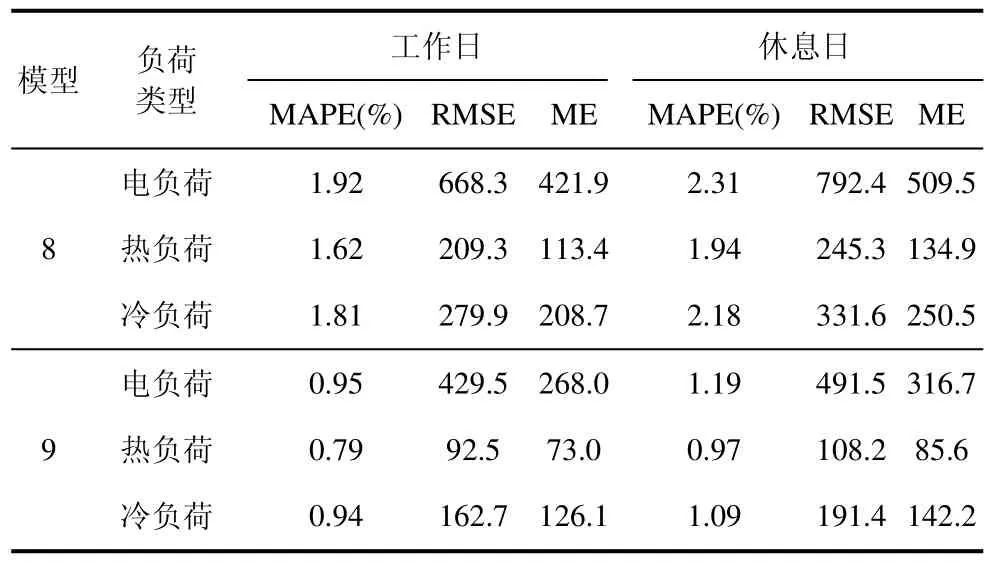
表4 误差补偿模型对预测误差的影响

图9 所示为考虑误差补偿与不考虑误差补偿下的电负荷、冷负荷、热负荷预测结果。

图9 误差补偿对负荷预测的影响

从表4 可以看出，考虑误差补偿的预测模型，对多元负荷的预测效果更佳，相较于不考虑误差补偿的预测模型，在工作日时电负荷、冷负荷和热负荷预测的MAPE分别减少了0.97%、0.87%和0.82%，RMSE 分别减少了35.1%、41.8%和55.8%，ME 分别减少了36.5%、39.6%和35.6%。误差补偿模型对电负荷的预测精度提升最为明显，对冷负荷和热负荷的预测精度提升大致相同。

5.4 不同模型对预测精度的影响

为进一步说明本文所提模型在综合能源系统多元负荷预测中的优势，将本文构建的模型与LSTM-LSTM 和GRU-GRU 组合模型进行对比。使用模型10 表示本文中构建的负荷预测模型；模型11 表示LSTM-LSTM 负荷预测模型，即使用LSTM模型进行负荷预测，使用LSTM 模型进行误差补偿；模型12 表示GRU-GRU 负荷预测模型，即使用GRU模型进行负荷预测，使用GRU 模型进行误差补偿。模型11 与模型12 均采用与模型10 相同的平台，同时模型参数也均采用本文模型使用的参数寻优方法，以保证对比试验的公平性。另外，为了进一步对比上述三种组合模型在训练和预测时间上的优劣，采用tic/toc 方法分别计算三种模型的训练时间和预测时间。各组合模型预测误差如表5 所示，各组合模型的训练时间、预测时间如表6 所示。

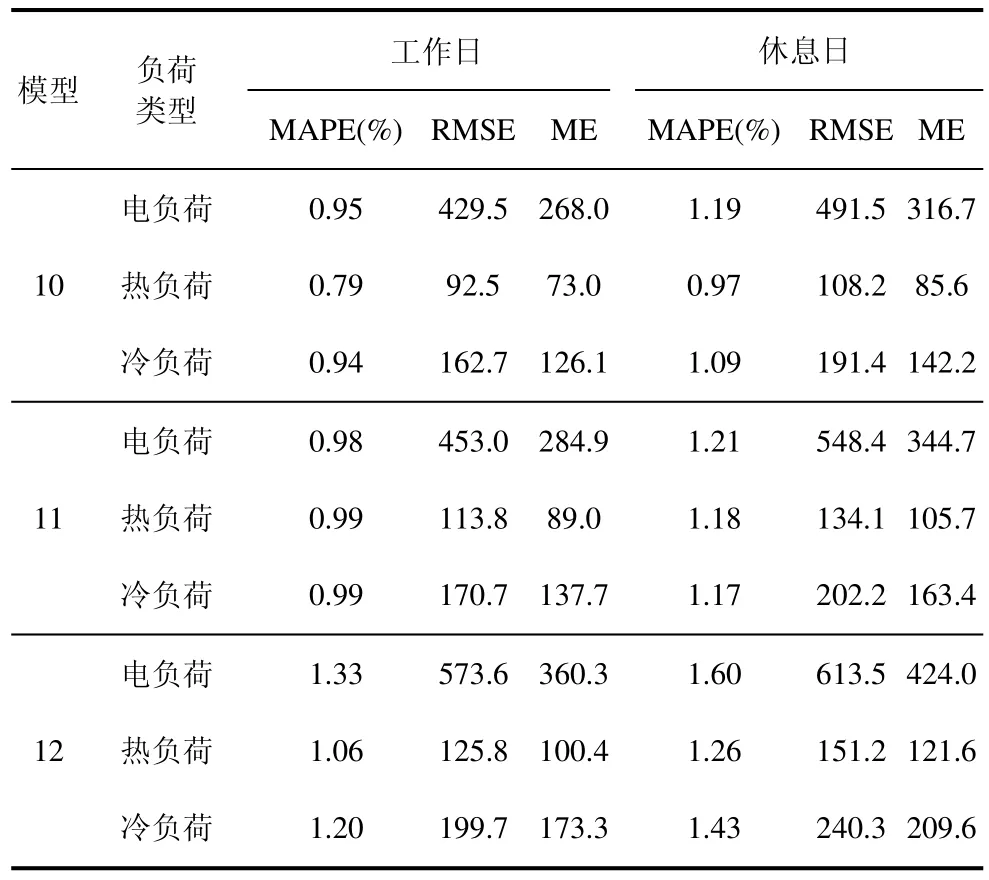
表5 不同模型的预测误差

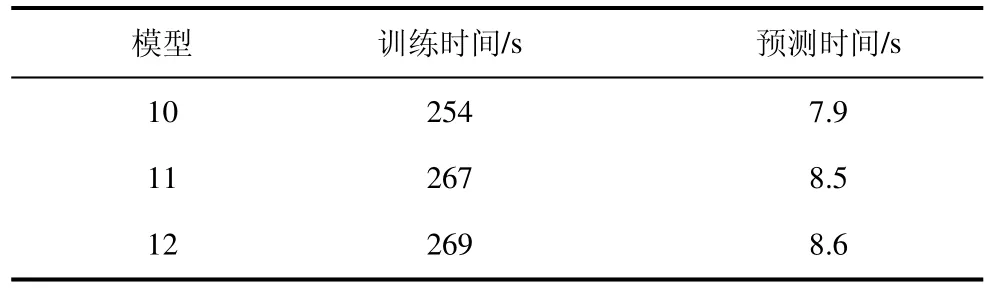
表6 不同模型的训练、预测时间

图10 所示为不同预测模型下的电负荷、冷负荷、热负荷预测结果。

图10 不同模型下的负荷预测结果

从表5 可以看出，本文所构建的预测模型相比于其他预测模型，在工作日时电负荷预测的MAPE降低了0.03%和0.38%，RMSE 降低了4.5%和32.3%，ME 降低了5.9%和25.6%；冷负荷预测的MAPE 降低了0.05%和0.26%，RMSE 降低了5.1%和22.7%，ME 降低了7.9%和27.3%；热负荷预测的MAPE 降低了0.19%和0.26%，RMSE 降低了18.7%和26.5%，ME 降低了8.4%和26.9%。由表6可以看出，对于本文所构建的多元预测模型，训练时间比模型11 和模型12 快了13 s 和15 s，预测时间比模型11 和模型12 快了0.6 s 和0.7 s。在预测精度和时间两方面充分说明了本文所提负荷预测模型的精确性和优越性。同时，从对比结果可知，这几种组合模型都可以有效地对多元负荷进行预测。在负荷趋势变动不大的地方，三种组合模型的预测误差大致相同，但是在负荷趋势波动较大的峰谷周围，本文模型相比于其他两个模型可以更好地拟合负荷曲线，误差更小。同时，由于电负荷响应极快，影响因素相对较多，导致了电负荷预测误差相比于热负荷和冷负荷略有增高。从预测结果还可得知，由于工作日的数据量大于休息日的数据量，因此该模型对工作日的多元负荷预测精度略高于休息日的多元负荷预测精度。

6 结论

本文利用LSTM 网络对多元负荷进行预测，并利用GRU 网络对预测误差进行补偿，将预测结果与误差重构为负荷预测最终结果，可以得出如下结论。

(1) 本文提出的误差补偿模型对电负荷、冷负荷和热负荷的预测精度提升分别为0.974%、0.878%和0.825%。

(2) 通过对比不同的预测模型与误差补偿模型，本文所提模型均具有最佳预测精度，验证了本文模型在负荷预测方面的优越性。

(3) 本文提出的综合能源系统多元负荷预测模型的算例数据来自美国亚利桑那州立大学创建的能源信息系统和“Campus Metabolism”网站，不存在突发事件、用电器故障或传感器故障等因素导致的负荷数据包含噪声的问题。在实际应用中，负荷数据可能会受到上述因素的影响而产生包含噪声的数据，在进行训练和预测之前需要对数据中的异常数据和缺失数据进行处理，从而提高该模型的预测精度。